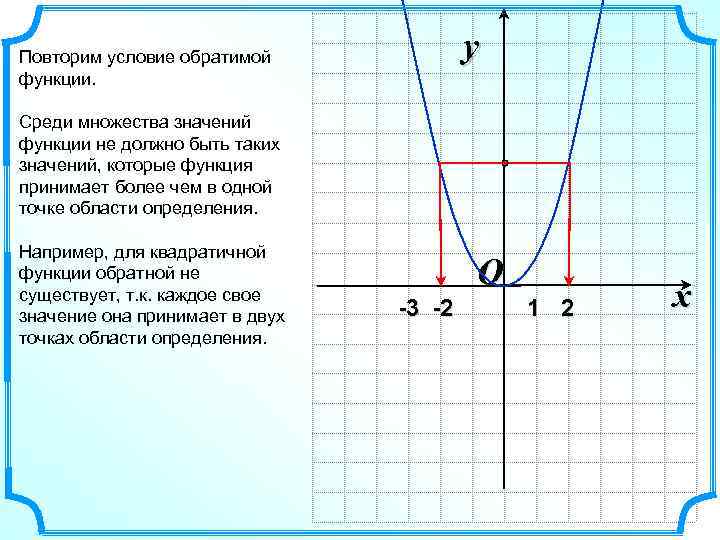
y Повторим условие обратимой функции. Среди множества значений функции не должно быть таких значений, которые функция принимает более чем в одной точке области определения. Например, для квадратичной функции обратной не существует, т. к. каждое свое значение она принимает в двух точках области определения. O -3 -2 1 2 x
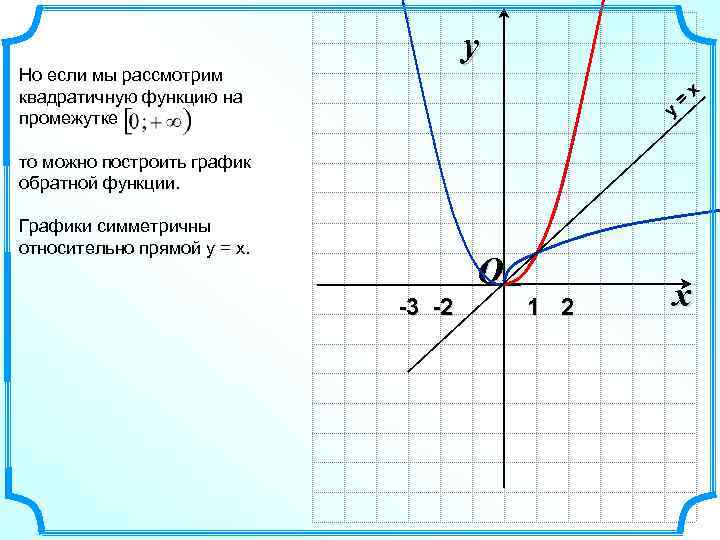
y Но если мы рассмотрим квадратичную функцию на промежутке у = то можно построить график обратной функции. Графики симметричны относительно прямой у = х. O -3 -2 1 2 x х
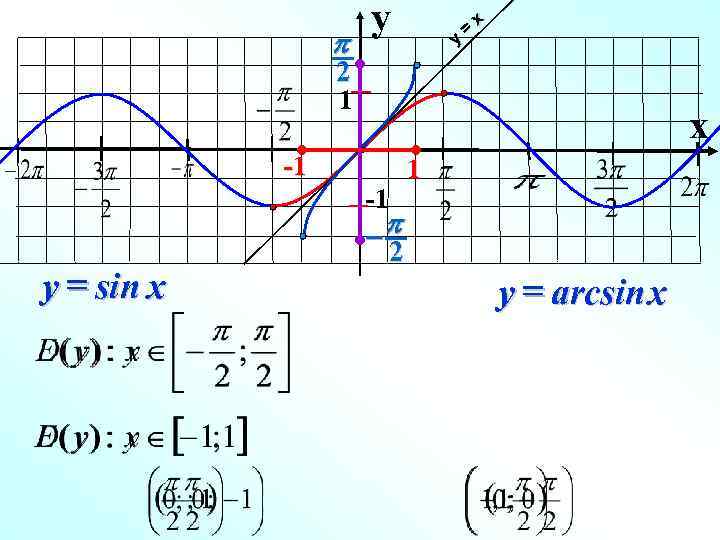
p y у = х 2 1 x -1 y = sin x -1 -p 2 1 y = arcsin x
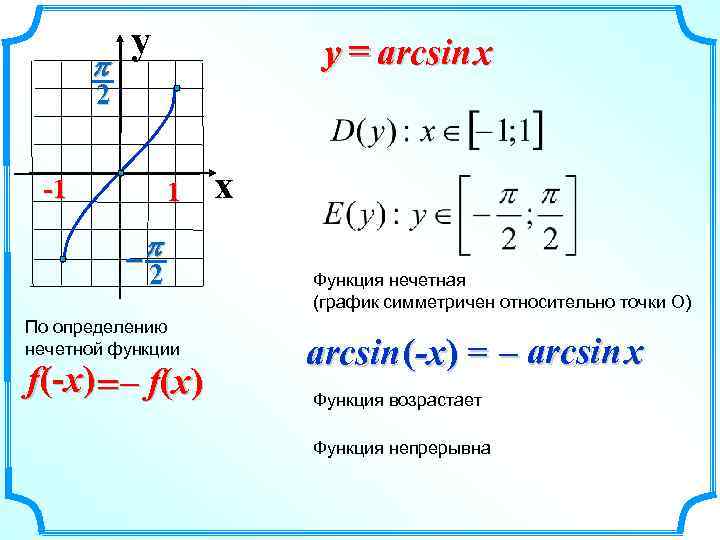
p y y = arcsin x 2 -1 1 p - 2 По определению нечетной функции f(-x) = – f(x) x Функция нечетная (график симметричен относительно точки О) arcsin (-x) = – arcsin x Функция возрастает Функция непрерывна
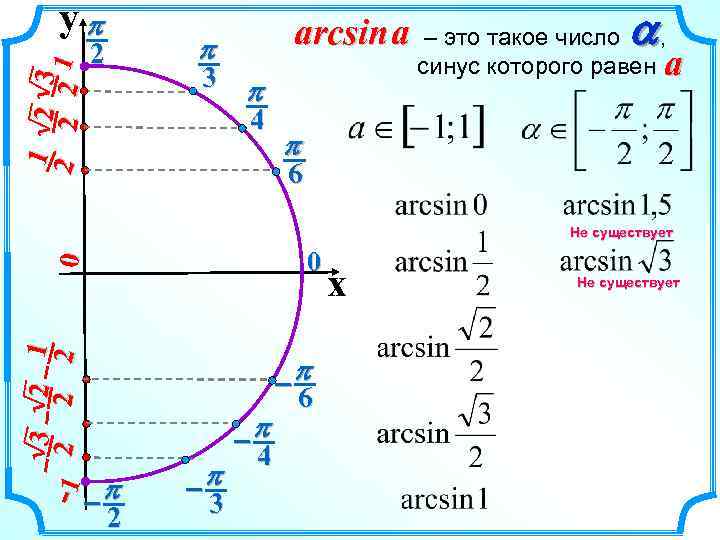
yp p 2 1 2 3 2 2 2 1 arcsin a 3 p 4 a – это такое число , синус которого равен a p 6 Не существует 3 2 1 -1 2 2 2 0 0 p -p 2 -p 3 -p 4 6 x Не существует
arcsin a a – это такое число , синус которого равен a arcsin (-x) = – arcsin x
Сравнить > т. к. y = arcsin x возрастающая функция Большему значению аргумента соответствует большее значение функции >
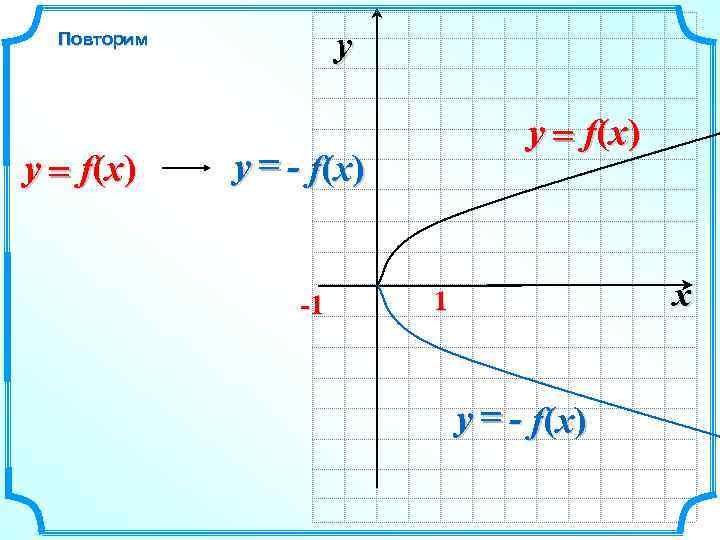
y Повторим y = f(x) y = - f(x) -1 x 1 y = - f(x)
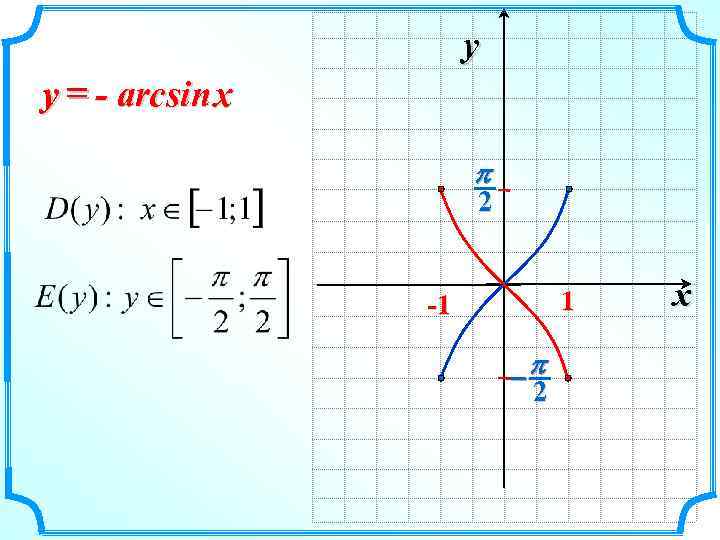
y y = - arcsin x p 2 1 -1 -p 2 x
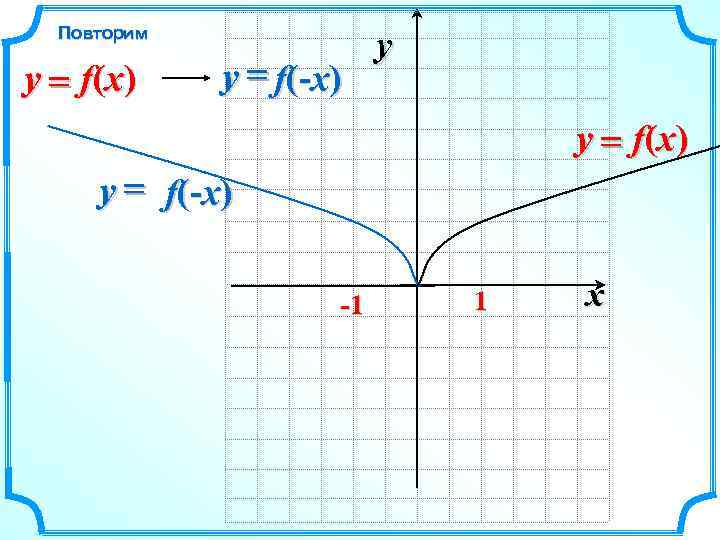
Повторим y = f(x) y = f(-x) y y = f(x) y = f(-x) -1 1 x
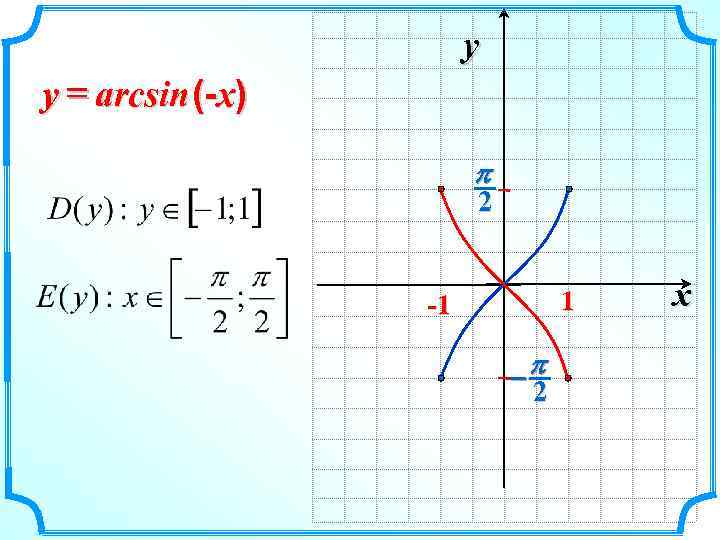
y y = arcsin (-x) p 2 1 -1 -p 2 x
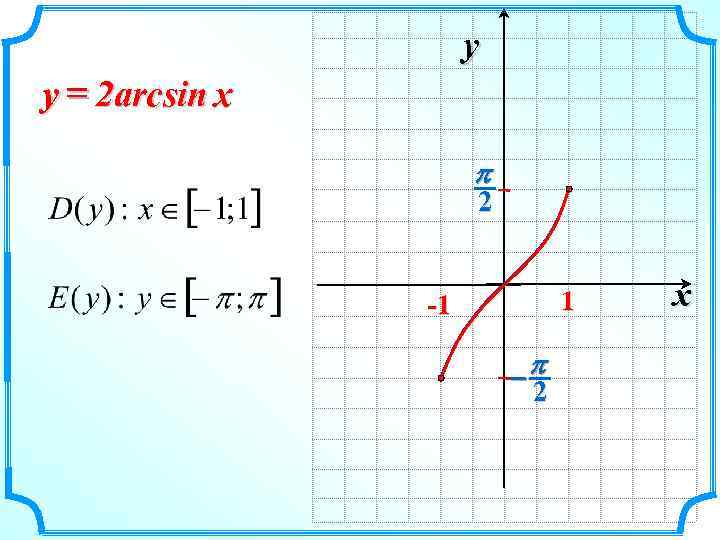
y y = 2 arcsin x p 2 1 -1 -p 2 x
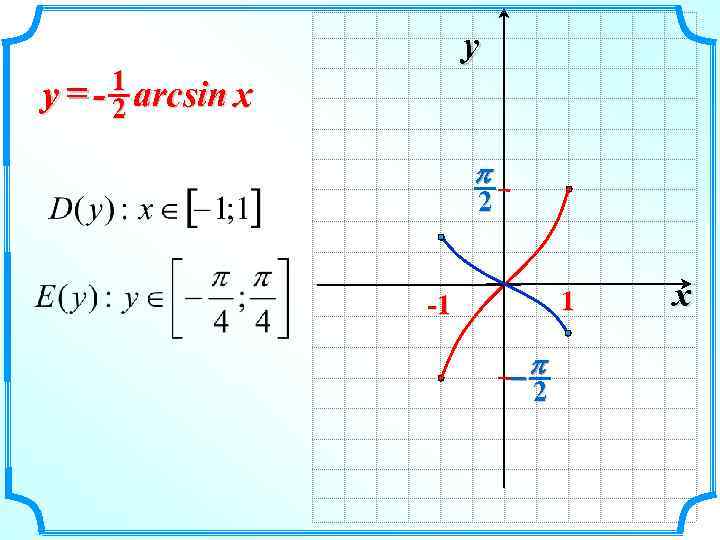
y = - 1 arcsin x y 2 p 2 1 -1 -p 2 x
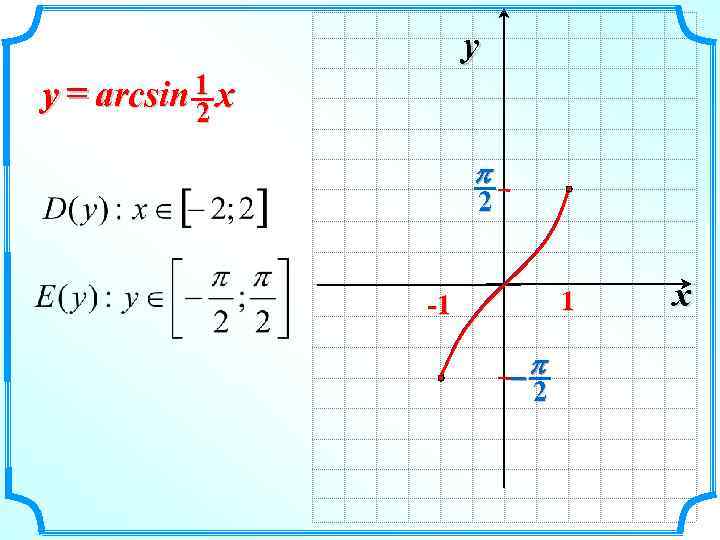
y y = arcsin 1 x 2 p 2 1 -1 -p 2 x
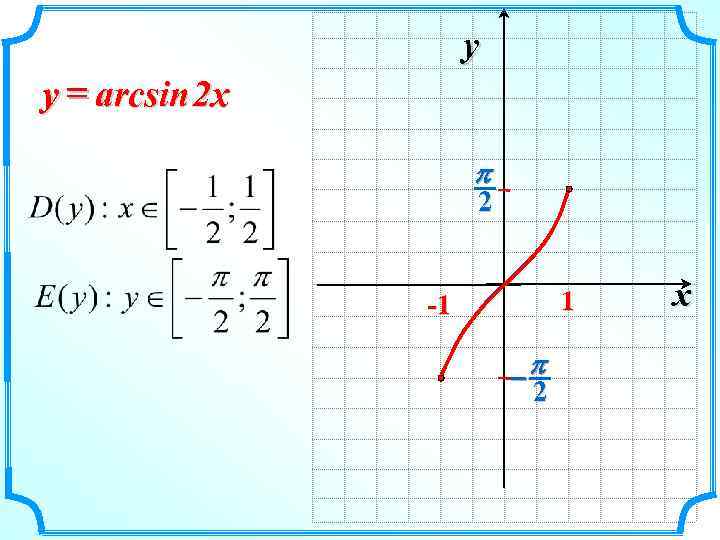
y y = arcsin 2 x p 2 1 -1 -p 2 x
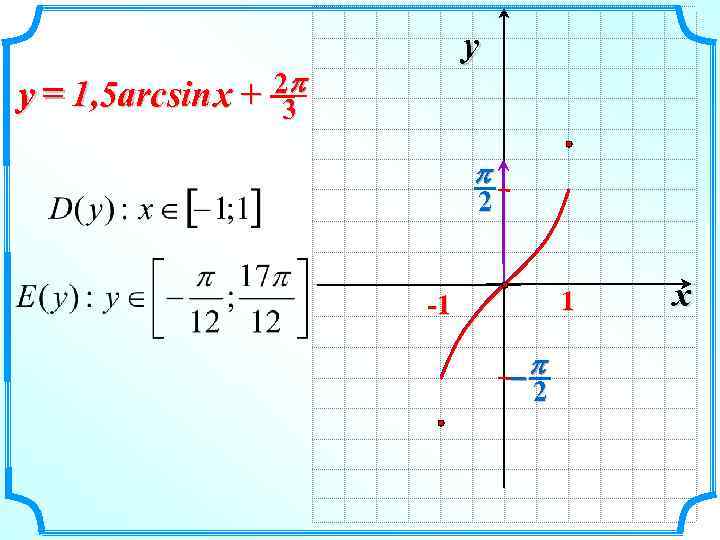
y = 1, 5 arcsin x + 23 p y p 2 1 -1 -p 2 x
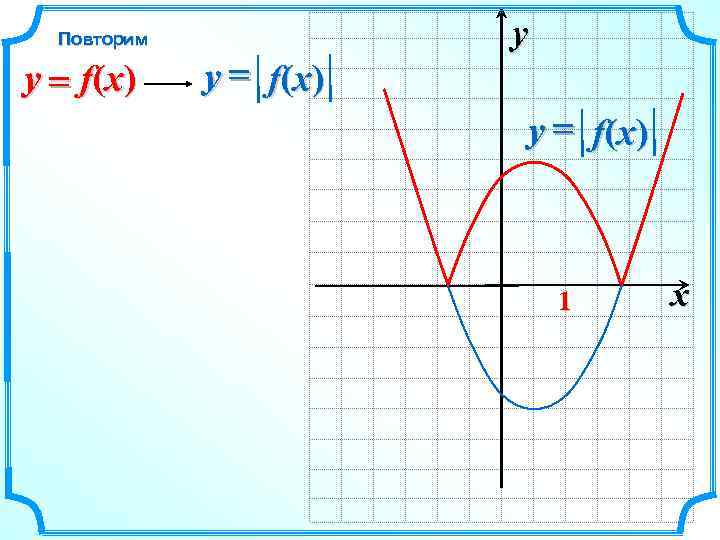
Повторим y = f(x) y y = f(x) 1 x
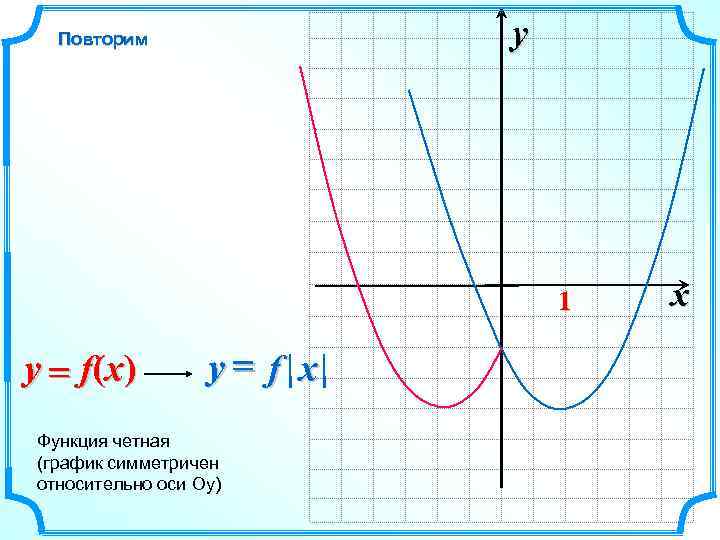
y Повторим 1 y = f(x) y= f x Функция четная (график симметричен относительно оси Оу) x
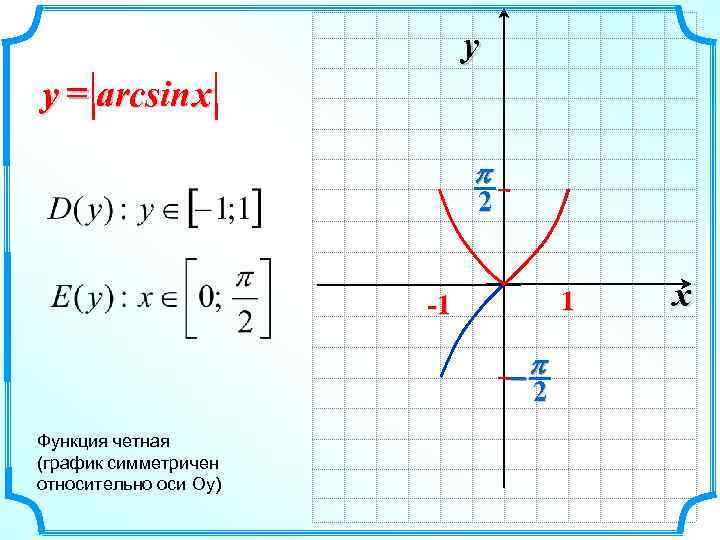
y y = arcsin x p 2 1 -1 -p 2 Функция четная (график симметричен относительно оси Оу) x
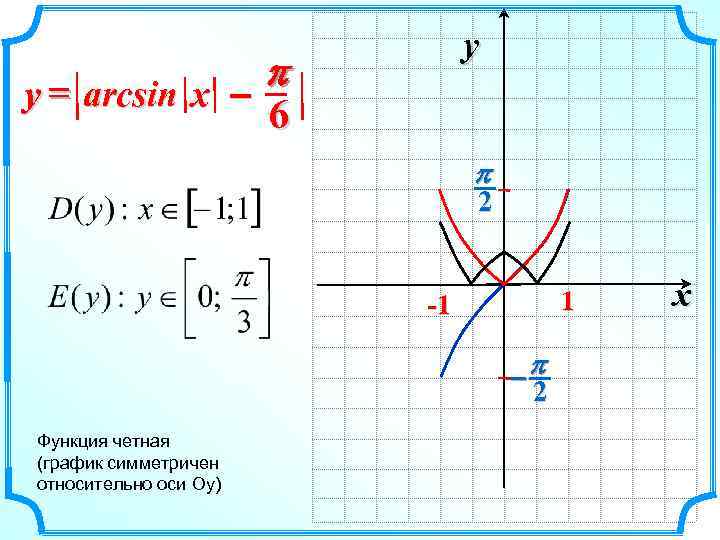
y p y = arcsin x – 6 p 2 1 -1 -p 2 Функция четная (график симметричен относительно оси Оу) x
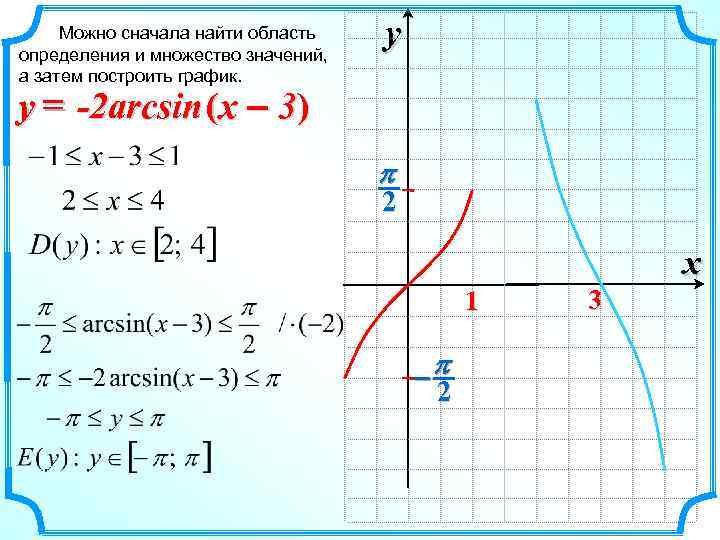
Можно сначала найти область определения и множество значений, а затем построить график. y y = -2 arcsin (x – 3) p 2 x 1 -p 2 3
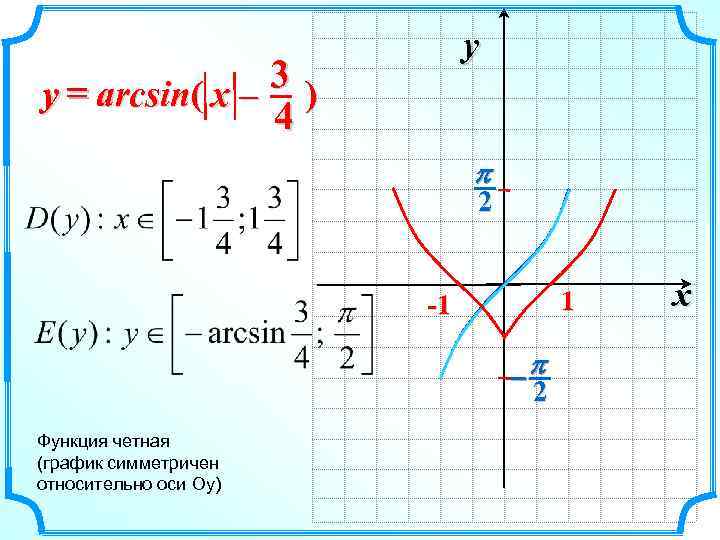
y 3) y = arcsin( x – 4 p 2 1 -1 -p 2 Функция четная (график симметричен относительно оси Оу) x
Скачать презентацию y Повторим условие обратимой функции Среди множества значений
14 arcsin.ppt