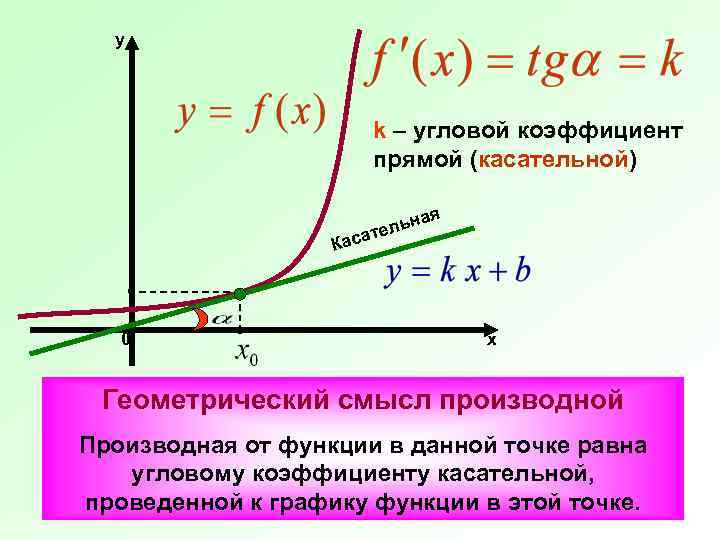
y k – угловой коэффициент прямой (касательной) ая

y k – угловой коэффициент прямой (касательной) ая льн ате Кас 0 х Геометрический смысл производной Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

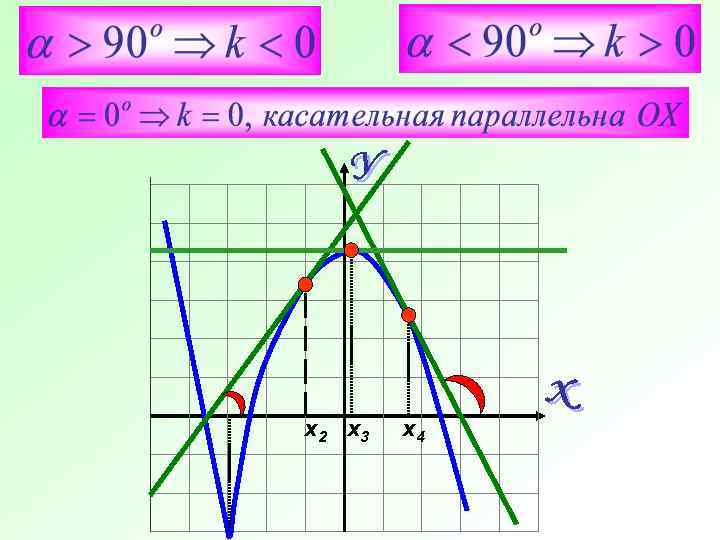х 2 х3 х4

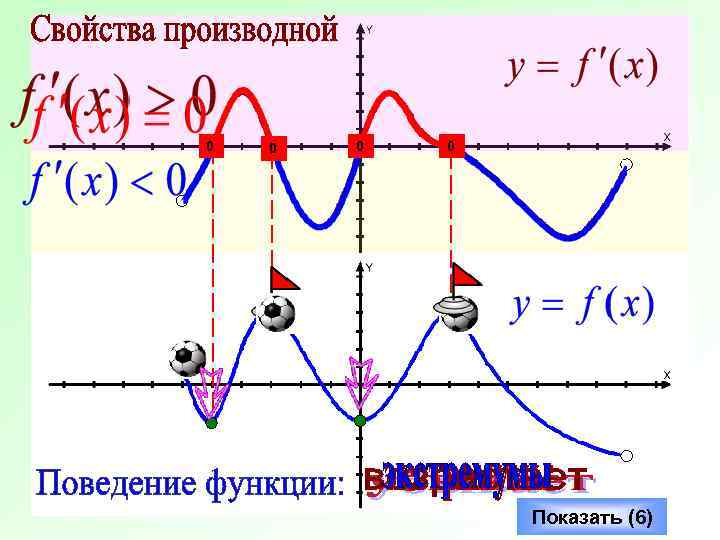0 0 Показать (6)

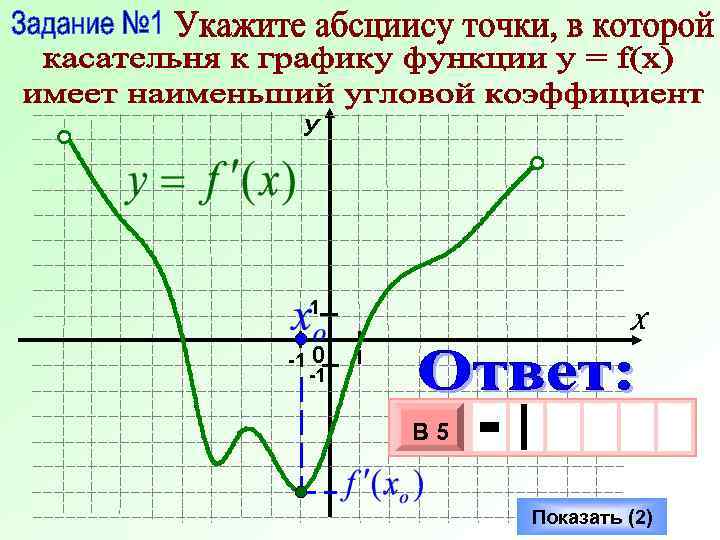У 1 -1 0 -1 Х 1 В 5 - 3 10 х х Показать (2)

Ищу наименьше значение производной В 5 - 3 10 х х Показать (2)

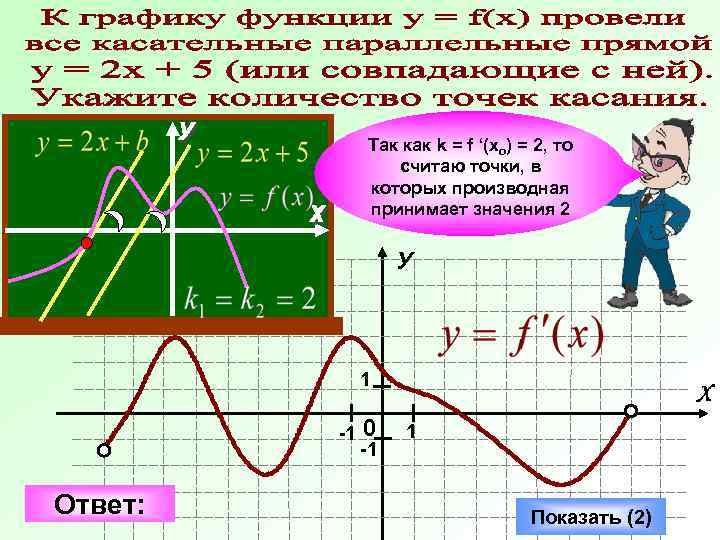Так как k = f ‘(xo) = 2, то считаю точки, в которых производная принимает значения 2 У 1 -1 Ответ: 0 -1 Х 1 Показать (2)

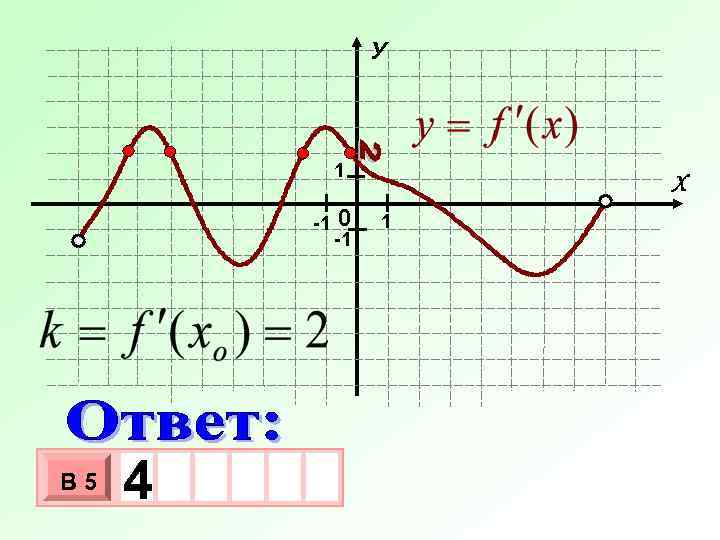У 1 -1 В 5 4 - 3 10 х х 0 -1 Х 1

У 1 -1 0 -1 Х 1

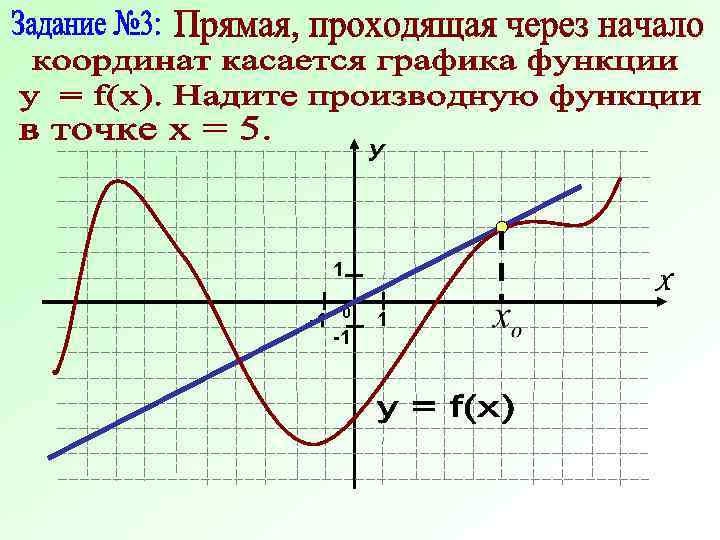
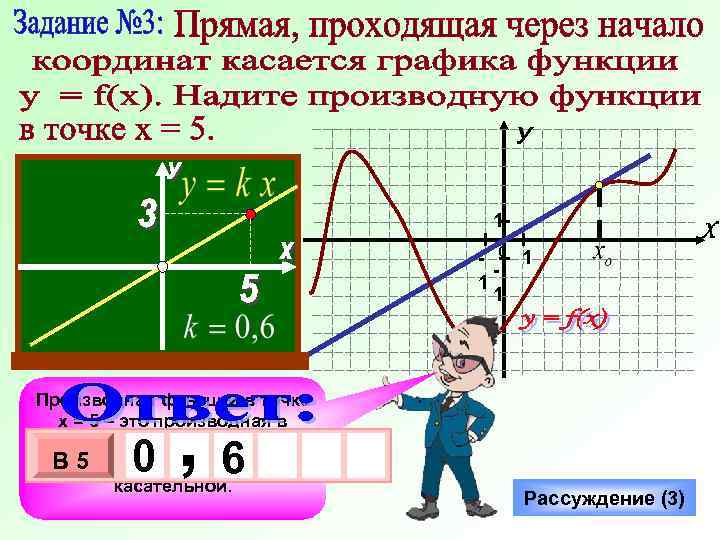У 1 - 0 1 1 1 Производная функции в точке х = 5 – это производная в точке касания хо, а она 3 равна х 1 0 х В 5 угловому коэффициенту касательной. , 6 0 Рассуждение (3) Х

У 1 -1 В 5 - 4 Ответ (2) 3 10 х х 0 -1 Х 1 Рассуждение (2)

y y = f (x) a 0 b В 5 7 - x 3 10 х х

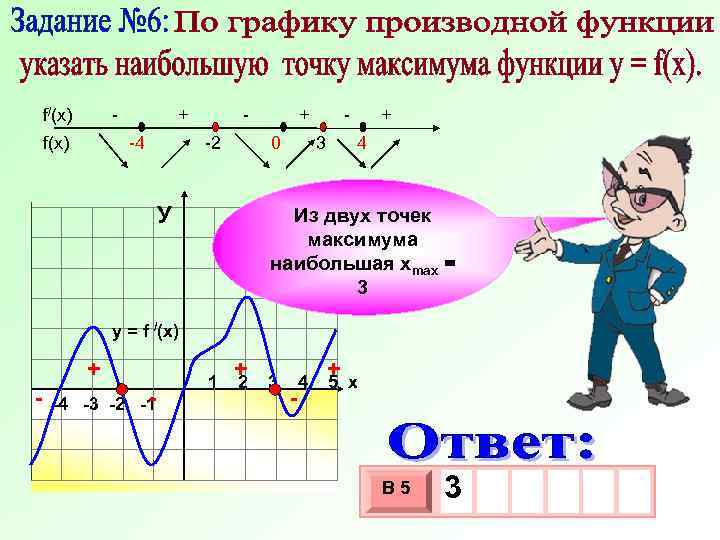f/(x) - + - + f(x) -4 -2 0 3 4 У Из двух точек максимума наибольшая хmax = 3 y = f /(x) + - -4 -3 -2 -1 1 + 2 3 - 4 +х 5 В 5 3 3 10 х х

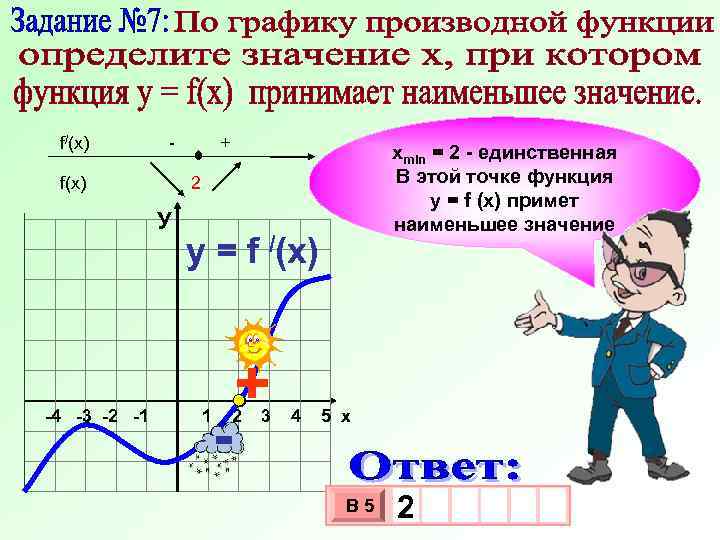f/(x) - + хmin = 2 - единственная В этой точке функция у = f (x) примет наименьшее значение f(x) 2 У -4 -3 -2 -1 y=f - /(x) + 1 2 3 4 5 х В 5 2 3 10 х х

y y = f (x) a b 0 В 5 2 x 3 10 х х

В 5 0 , 5 3 10 х х

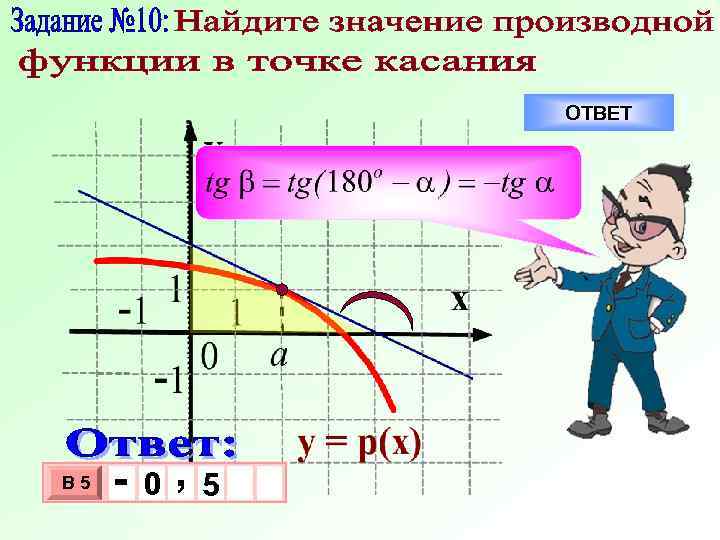ОТВЕТ В 5 - 0 , 5 3 10 х х

3 2 -2 -3 В 5 9 3 10 х х

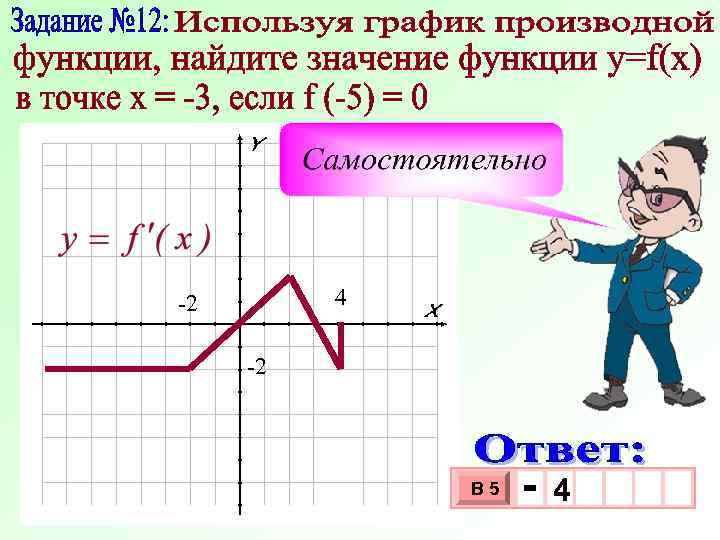4 -2 -2 В 5 - 4 3 10 х х

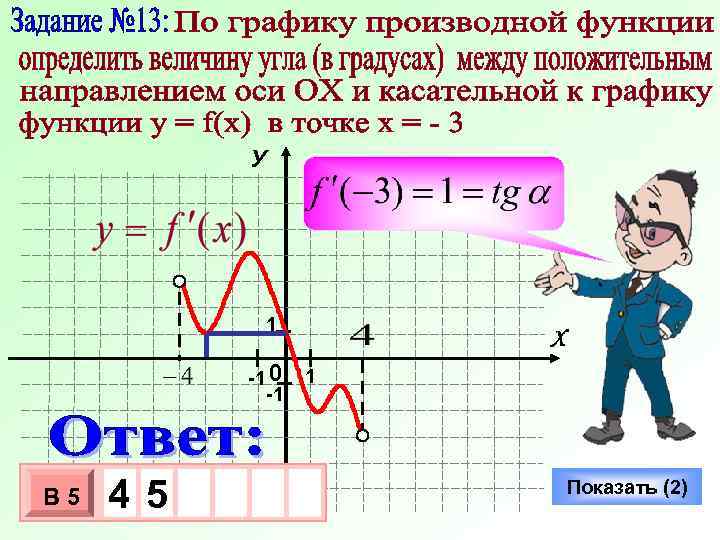У 1 -1 0 -1 В 5 4 -5 3 10 х х Х 1 Показать (2)

У f ’ (x) = 0 1 В 5 2 - -1 0 -1 3 10 х х Х 1

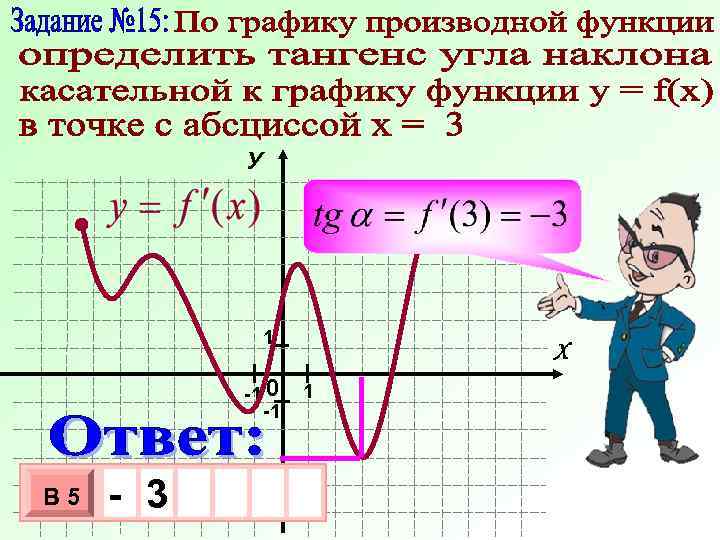У 1 -1 0 -1 В 5 -3 3 10 х х Х 1

У 1 -1 В 5 - 4 Ответ 3 10 х х 0 -1 Х 1 Рассуждение (2)

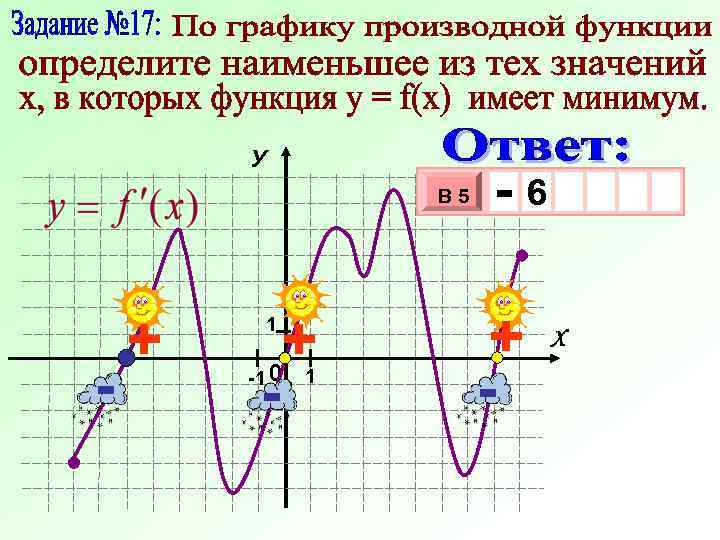У В 5 - + 1 - + -1 0 -1 1 -6 + - 3 10 х Х х

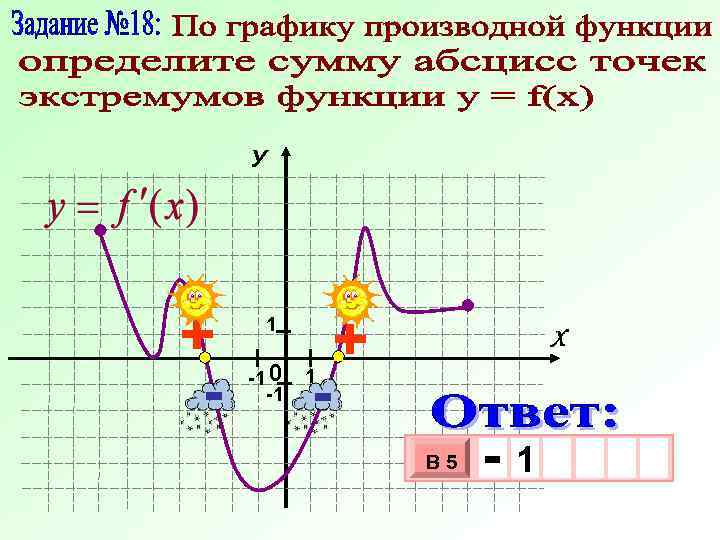У + - 1 -1 0 -1 - 1 + Х В 5 -1 3 10 х х

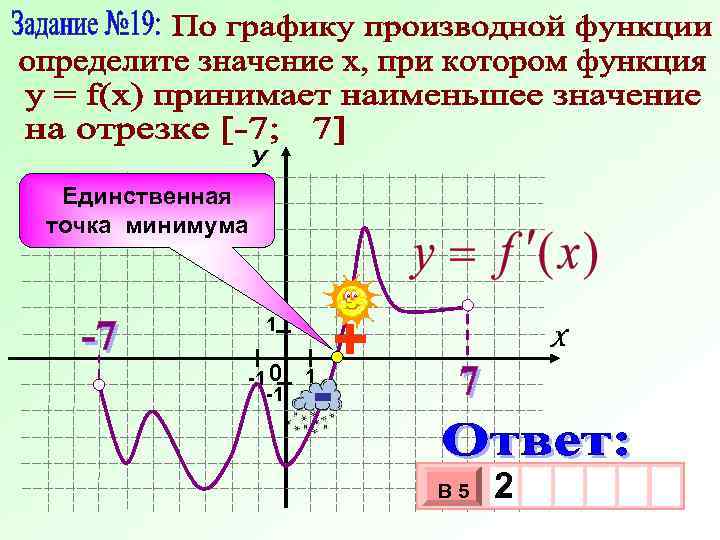У Единственная точка минимума 1 -1 0 -1 - 1 + Х В 5 2 3 10 х х

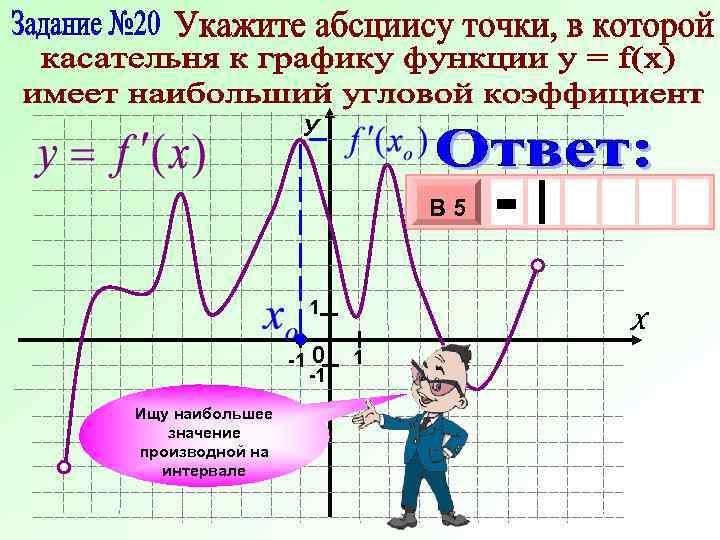У В 5 1 -1 0 -1 Ищу наибольшее значение производной на интервале - х 3 10 х Х 1