y B z Δb n db dt A

Зарегистрируйтесь, чтобы просмотреть полный документ!

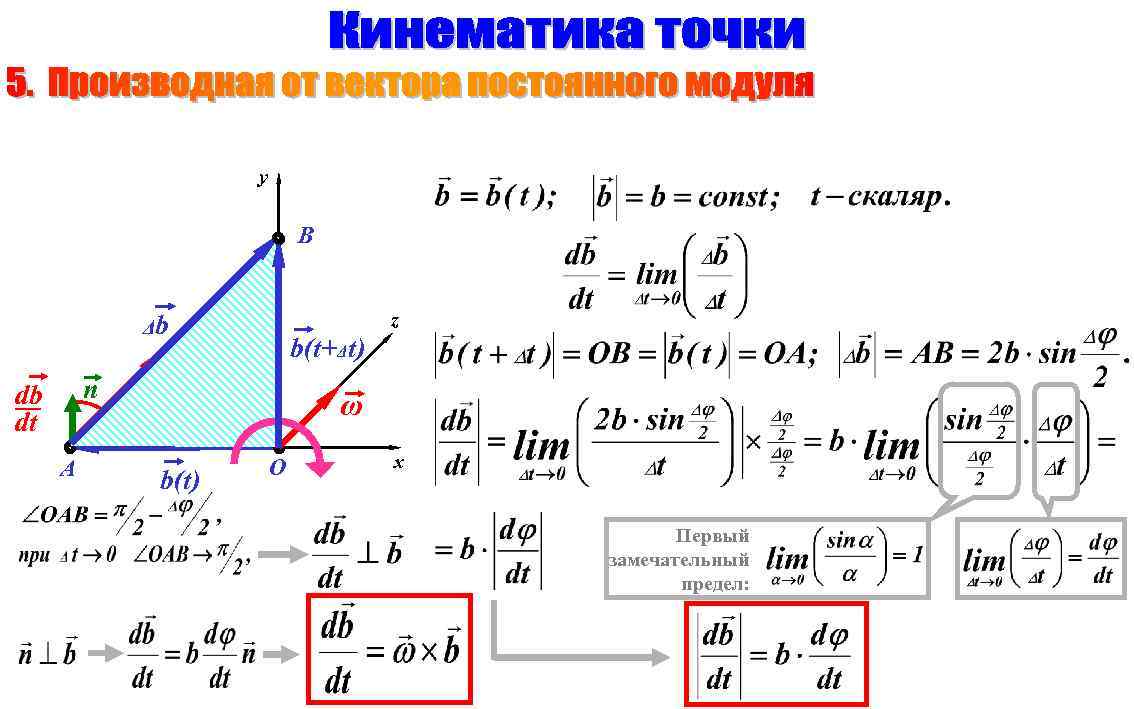
y B z Δb n db dt A Δb 900 Δt b(t) b(t+Δt) ω Δφ O x Первый замечательный предел:

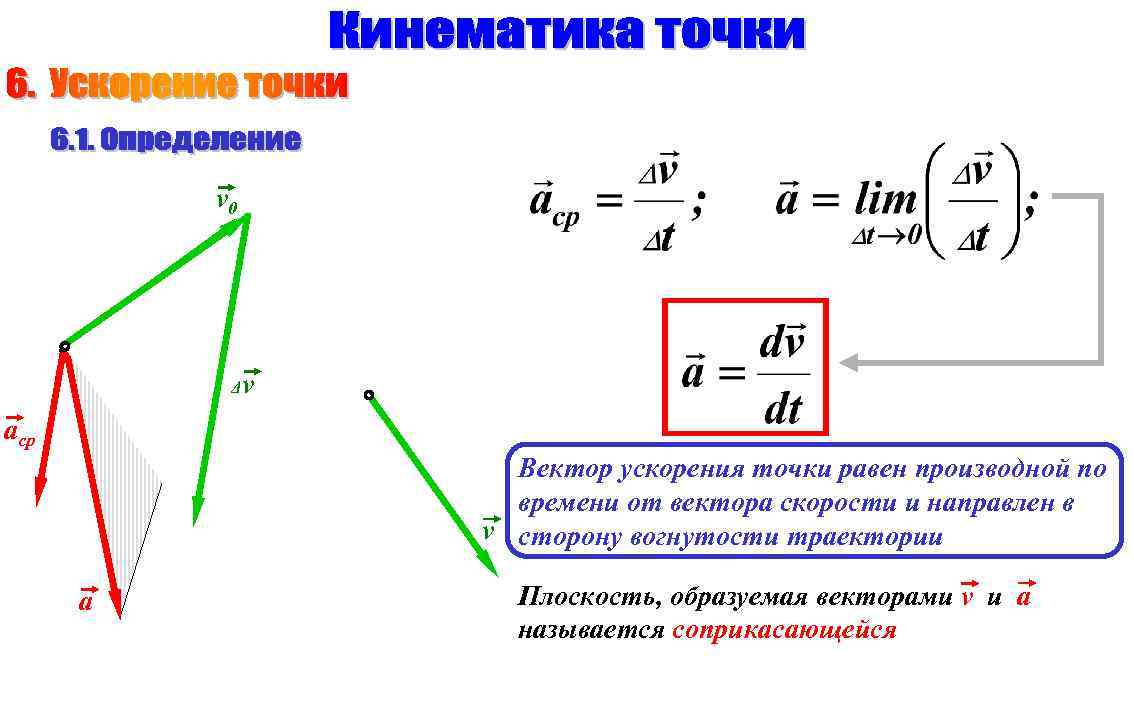
v 0 Δv aср Вектор ускорения точки равен производной по времени от вектора скорости и направлен в v сторону вогнутости траектории a Плоскость, образуемая векторами v и a называется соприкасающейся

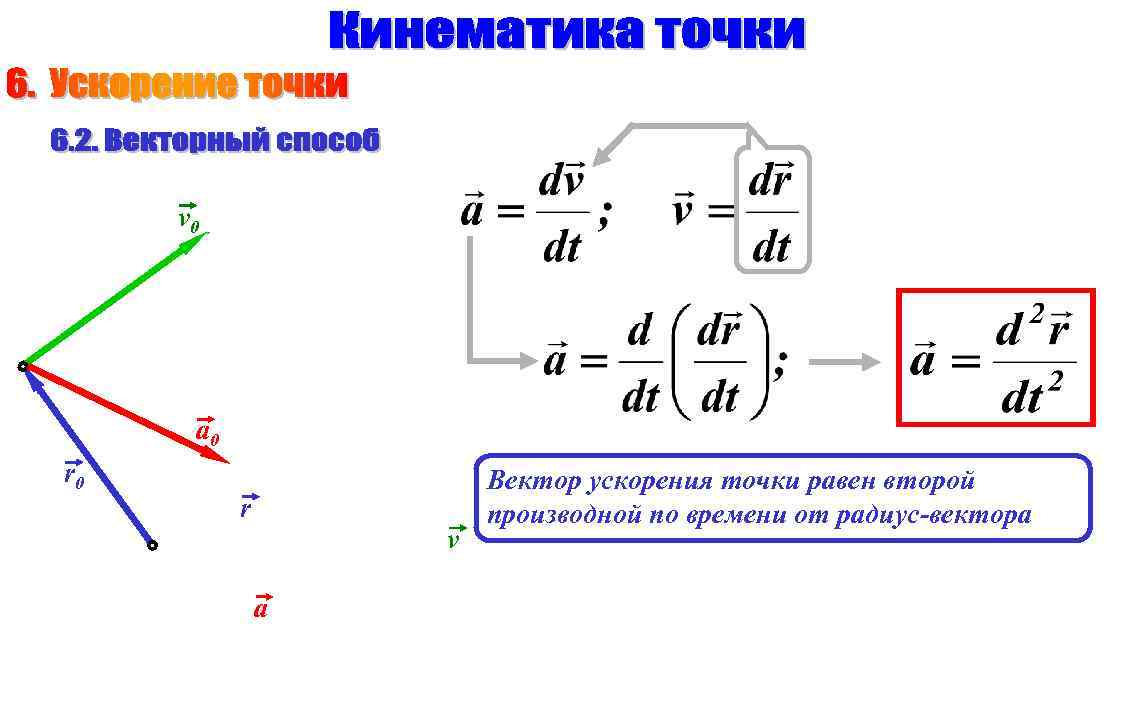
v 0 a 0 r v a Вектор ускорения точки равен второй производной по времени от радиус-вектора

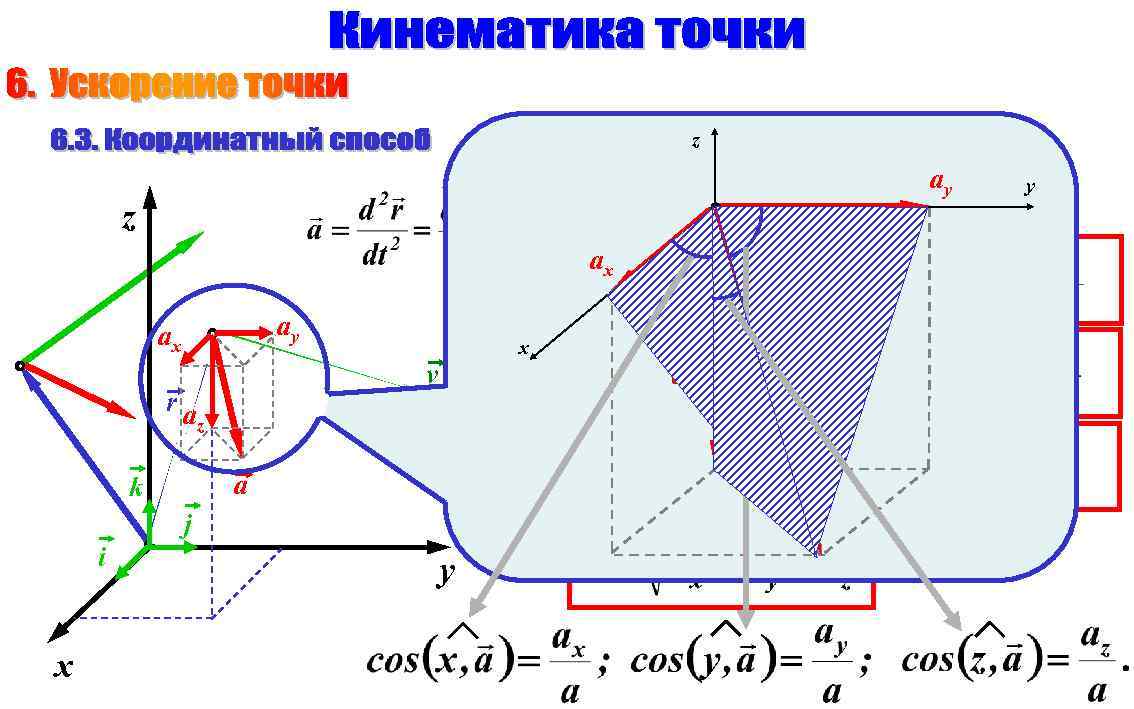
z ay z ax ay ax x v ra az z a k j i x y y

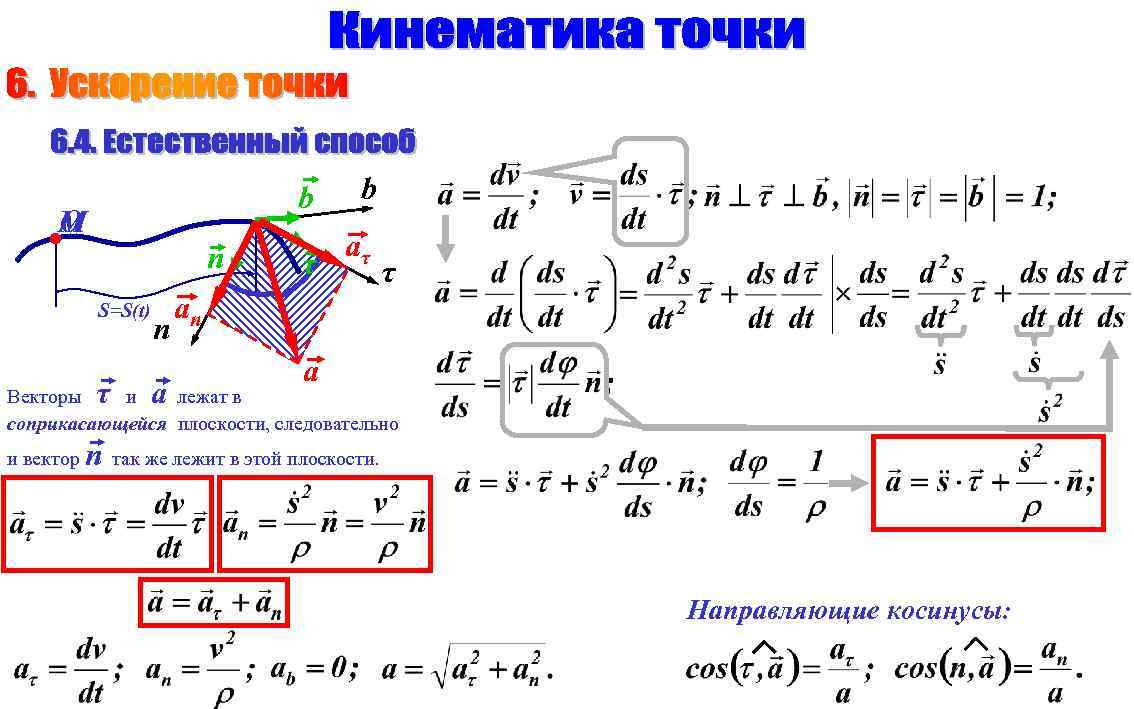
b М O n S=S(t) τ n a b τ aτ an τ a Векторы и лежат в соприкасающейся плоскости, следовательно и вектор n так же лежит в этой плоскости. Направляющие косинусы:

Движение точки называется равнопеременным, если aτ = const aτ0 an aτ Частный случай – равнопеременное прямолинейное движение, an=0, a= aτ = const:

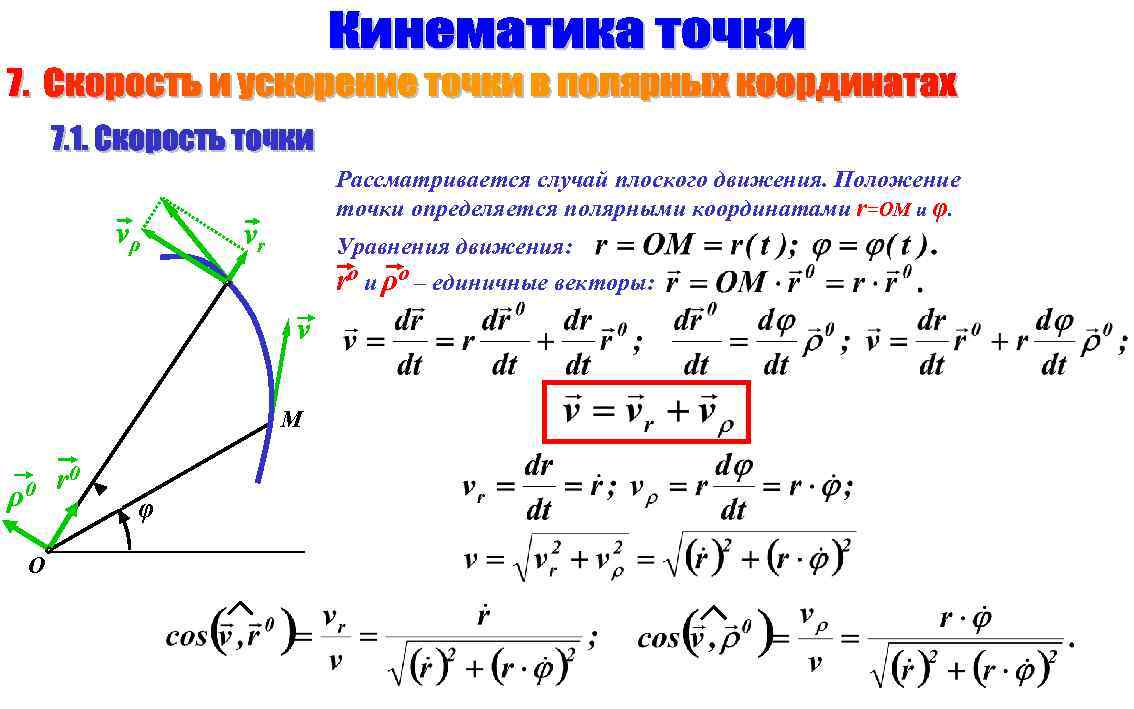
vρ Рассматривается случай плоского движения. Положение точки определяется полярными координатами r=OM и φ. vr Уравнения движения: ro и ρо – единичные векторы: v M ρ0 O r 0 φ

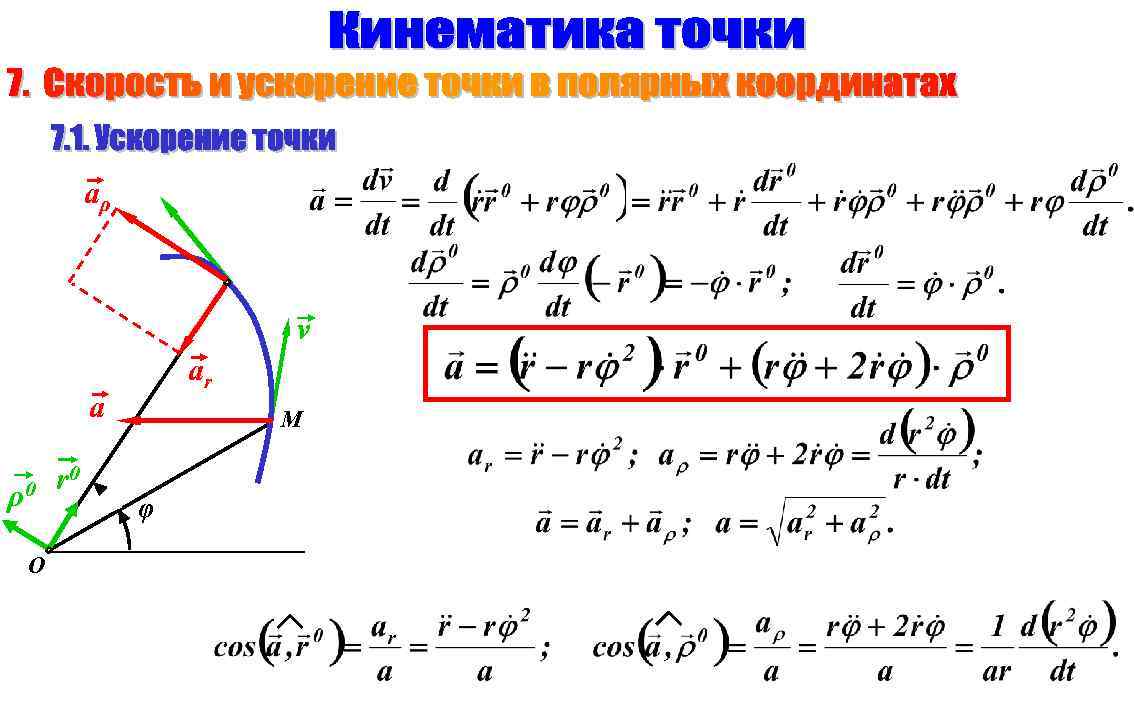
aρ v ar a ρ0 O r 0 M φ

Поезд, имея начальную скорость v 0 = 54 км/ч, прошел путь s = 600 м за время t 1 = 30 c. Считая движение поезда равнопеременным, определить скорость и ускорение поезда в конце 30 -й секунды, если рассматриваемое движение происходит на закруглении радиуса R = 1 км. Решение: aτ an v R a Ответ:

Точка движется по окружности R = 20 см против хода часовой стрелки по закону s = 5π·t см. Найти уравнение траектории точки, если ось Ох проходит через ее начальное положение. Определить скорость и ускорение точки в момент времени t = 1 c. y Решение: v Траектория: vy ax y(t) an ≡ a O vx Скорость: ay s α R Нормальное ускорение: x(t) x Ускорение: Касательное ускорение: Ответ:

Движение точки задано уравнениями x = 10 + 20·sin(4 t 2), y = 15 - 10·cos(4 t 2). Найти: Уравнение траектории точки. Скорость точки, ускорение точки, радиус кривизны траектории при t = π/10 c. Решение: 1. Траектория: y Эллипс с полуосями 20, 10 и центром, смещенным в точку с координатами (10, 15). x 1 М 0 y 1 При t = 0: М 1 x При t = π/10 c :

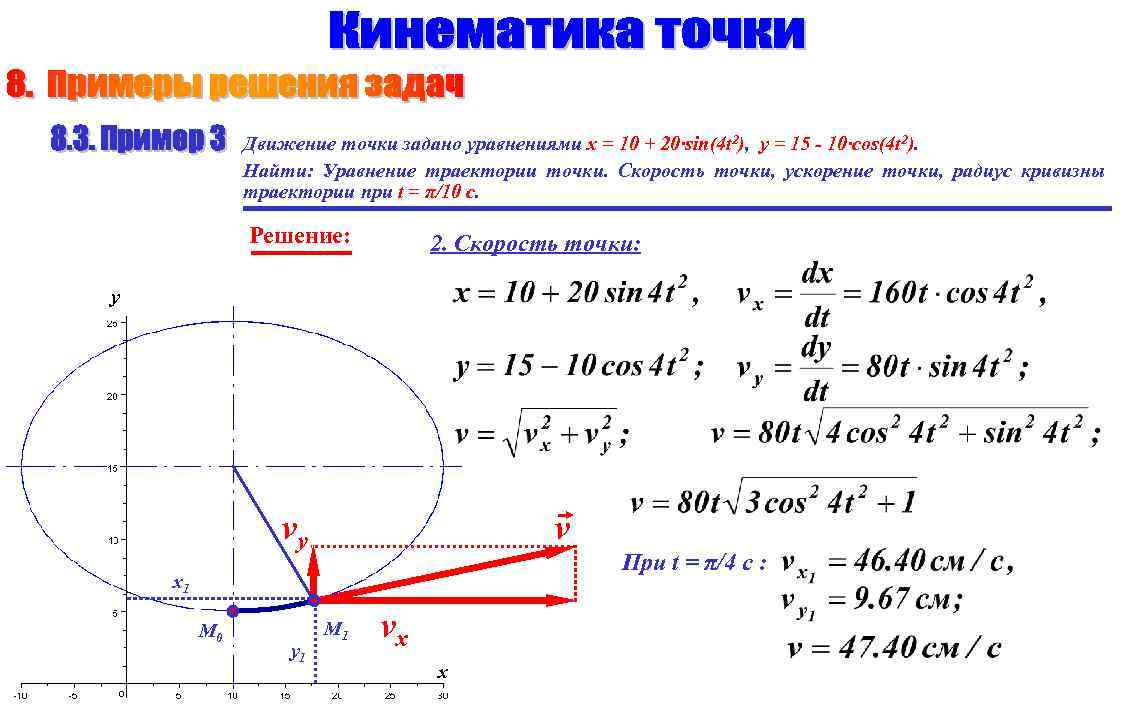
Движение точки задано уравнениями x = 10 + 20·sin(4 t 2), y = 15 - 10·cos(4 t 2). Найти: Уравнение траектории точки. Скорость точки, ускорение точки, радиус кривизны траектории при t = π/10 c. Решение: 2. Скорость точки: y v vy При t = π/4 c : x 1 М 0 y 1 М 1 vx x

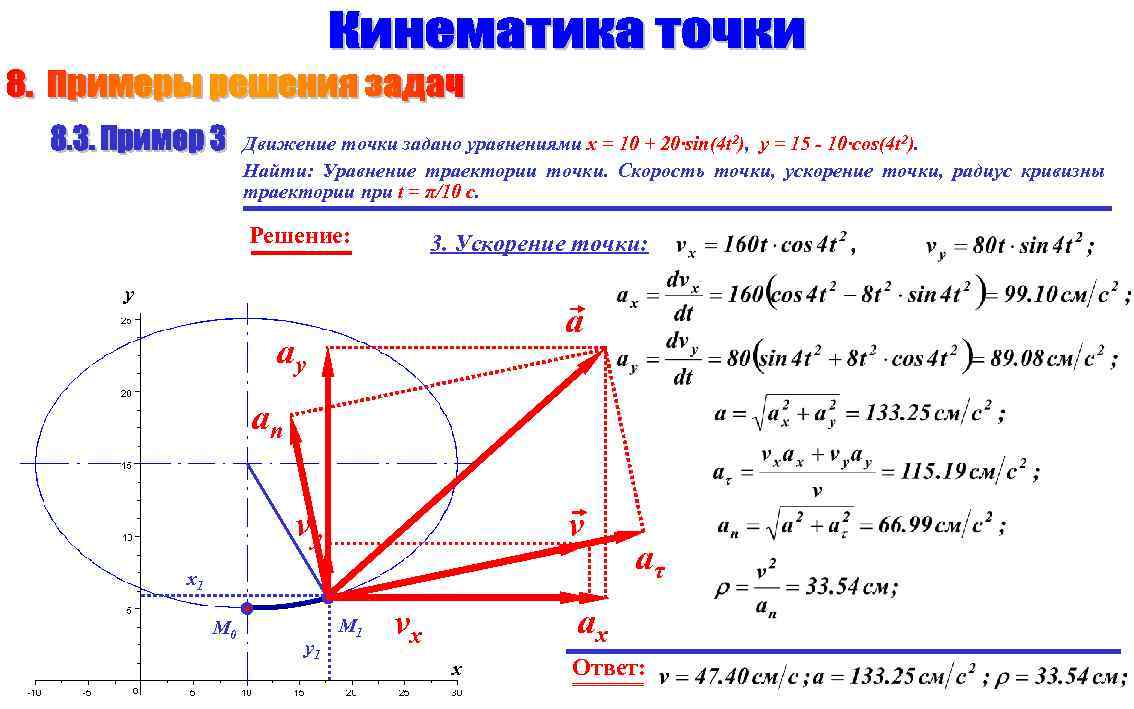
Движение точки задано уравнениями x = 10 + 20·sin(4 t 2), y = 15 - 10·cos(4 t 2). Найти: Уравнение траектории точки. Скорость точки, ускорение точки, радиус кривизны траектории при t = π/10 c. Решение: 3. Ускорение точки: y a ay an v vy x 1 М 0 y 1 М 1 aτ ax vx x Ответ:

Скачать презентацию y B z Δb n db dt A

Лекция 02(п) - Кинематика точки (ускорение).ppt

Количество слайдов: 13