XVII Электрические фильтры 17 1 Определения и

XVII Электрические фильтры

17. 1 Определения и классификация

Электрический фильтр – устройство, которое практически не ослабляет спектральные составляющие сигнала в заданной полосе частот и значительно ослабляет (подавляет) все спектральные составляющие вне этой полосы.

Полоса пропускания(ПП) – диапазон частот, в котором ослабление фильтра мало и не превышает некоторого допустимого (заданного ) значения Аmax Полоса непропускания (ПН)– диапазон частот, в котором ослабление фильтра велико и не меньше некоторого допустимого (заданного ) значения Аmin.

Классификация электрических фильтров 1. По расположению полосы пропускания на шкале частот : а) фильтры нижних частот (ФНЧ); б) фильтры верхних частот (ФВЧ); в) полосовой фильтр (ПФ); г) режекторный (заграждающий) фильтр (РФ).

2. По виду аппроксимирующей функции: а) полиномиальные б) дробные (со всплесками ослабления)

3. По виду применяемых элементов фильтры подразделяются на: а) пассивные LC-фильтры; б) активные RC-фильтры; в) пьезоэлектрические и магнитострикционные фильтры; г) фильтры на отрезках линий передач; д) электромеханические фильтры; е) цифровые фильтры.

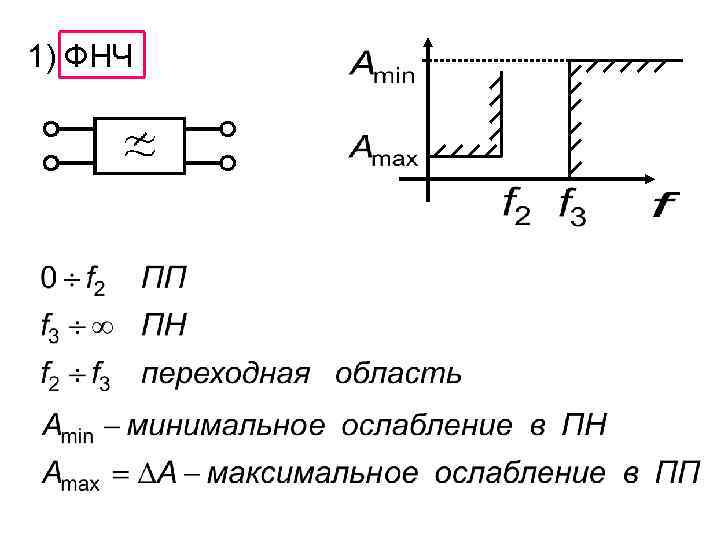1) ФНЧ

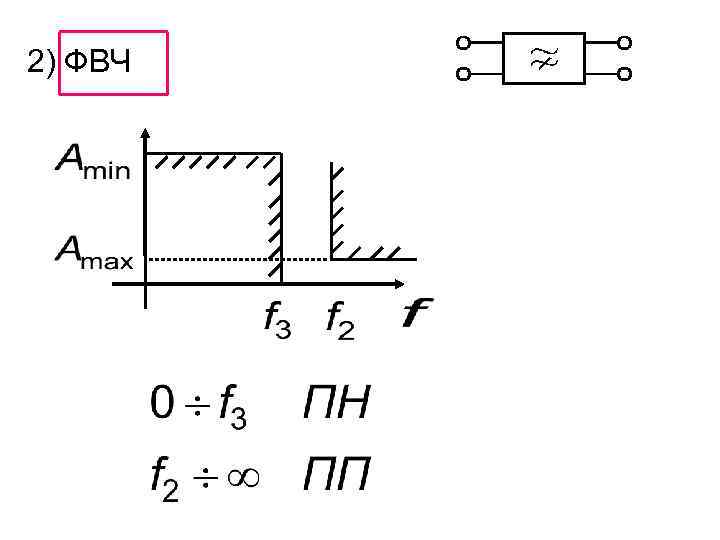2) ФВЧ

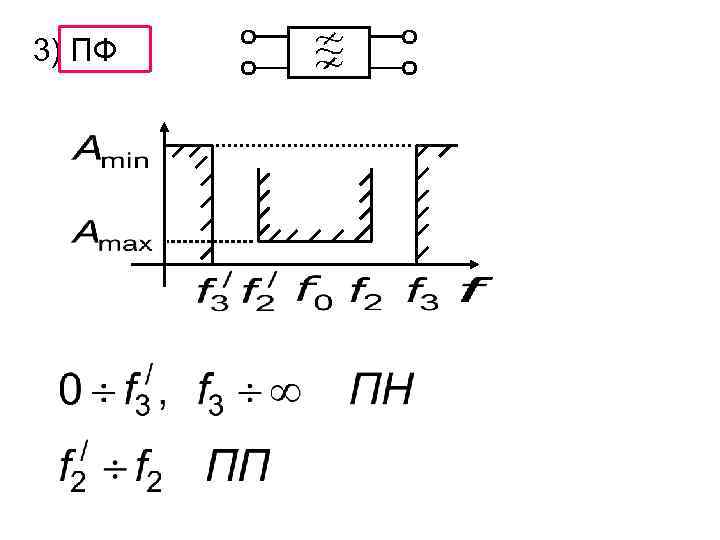3) ПФ

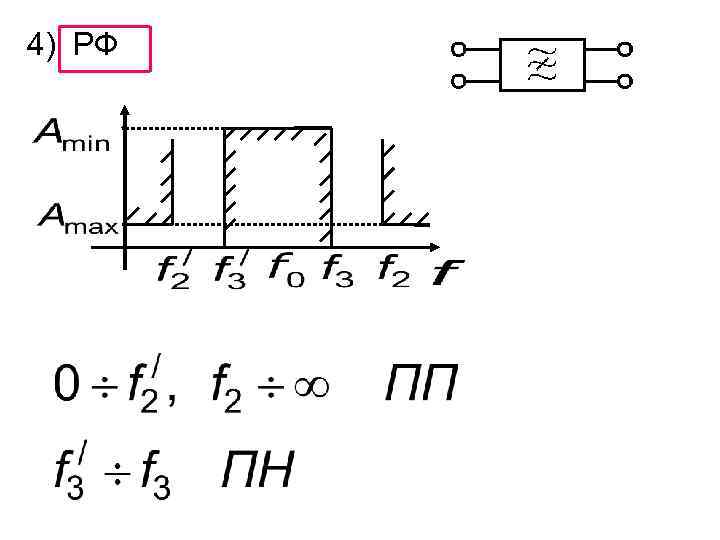4) РФ

17. 2 Требования к фильтру

1. Требования к характеристике ослабления 2. Требования к квадрату АЧХ

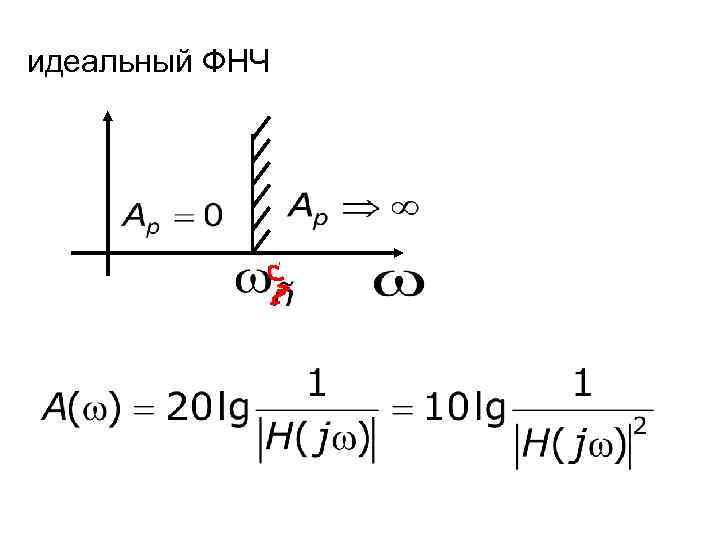идеальный ФНЧ

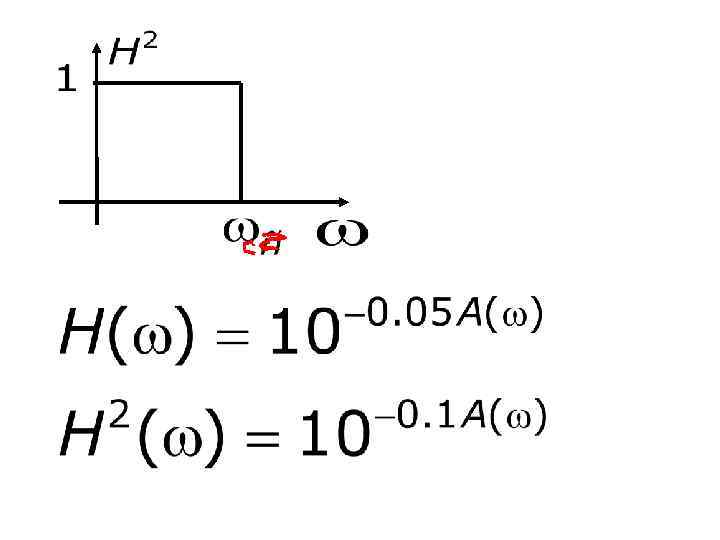
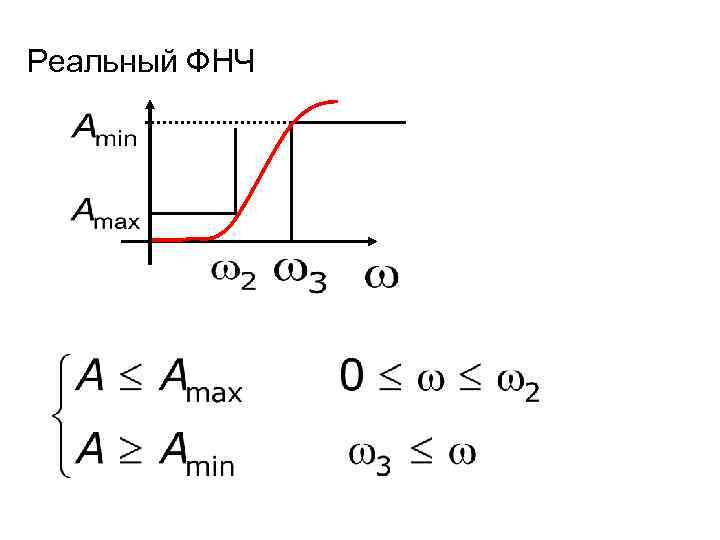Реальный ФНЧ

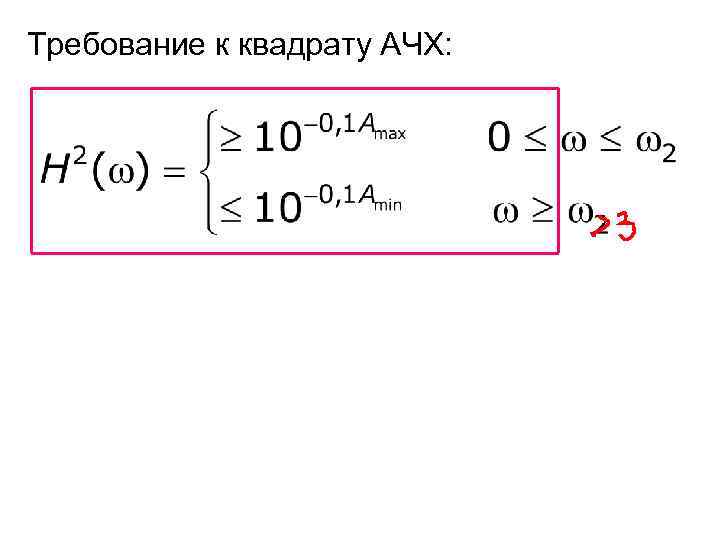Требование к квадрату АЧХ:

Передаточная функция фильтра передаточная функция ЧП где V(p) – полином Гурвица

Фильтр, как и ЧП, рассматривается в системе: источник сигнала – фильтр – нагрузка, т. е. как двусторонне нагруженный ЧП, работа которого описывается рабочей постоянной передачи. Обычно фильтр включается в согласованном режиме, а т. к. фильтр – симметричный ЧП, то

Передаточная функция ФНЧ второго порядка:

Передаточная функция ФВЧ второго порядка:

Передаточная функция ПФ второго порядка:

Порядок синтеза фильтра 1. Выполняется операция преобразования частот, при которой характеристики проектируемого фильтра пересчитываются на характеристики фильтра НЧ – прототипа 2. Выполняется операция нормирования по частоте

3) Выбирается характер аппроксимирующей функции и определяются ее параметры 4) Вычисляются корни и составляется передаточная функция НЧ – прототипа 5) Определяются элементы фильтра НЧ – прототипа. Реализуется схема 6) Осуществляется обратный переход от фильтра НЧ - прототипа, к исходному фильтру

НЧ – прототип - фильтр низких частот с нормированными значениями сопротивления и частоты - нормированное сопротивление - нормированная частота

Передаточная характеристика ФНЧ:

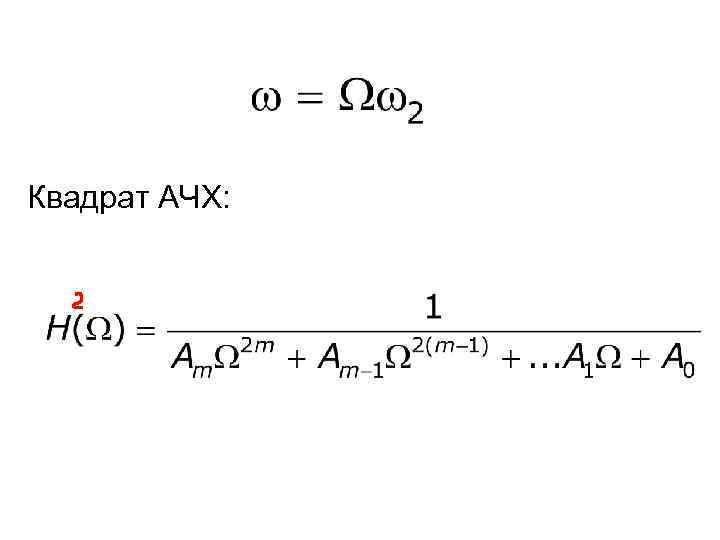Квадрат АЧХ:

ослабление:

17. 3 Аппроксимация передаточной функции

Задачи аппроксимации состоит в том, чтобы - найти аналитическое выражение передаточной функции цепи, удовлетворяющей требованиям, предъявляемому к фильтру - функция должна быть физически реализуема (УФР)

Условие физической реализации: 1) Н(р) - рациональная дробь, т. е. отношение двух многочленов переменной р. 2) Степень полинома числителя не больше степени полинома знаменателя 3) Полином знаменателя - полином Гурвица, т. е. его корни расположены в левой полуплоскости р.

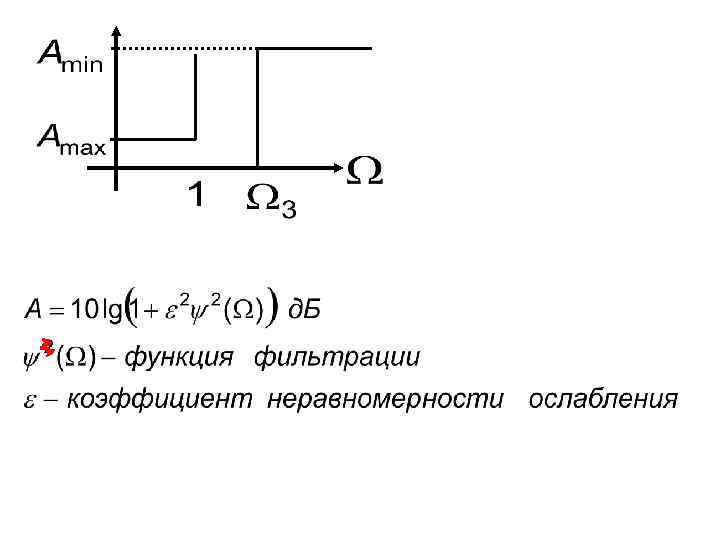
Требования к функции фильтрации Полиномы Чебышева или полиномы Баттерворта удачно синтезируют частотные характеристики фильтров

17. 4 Фильтры Баттерворта

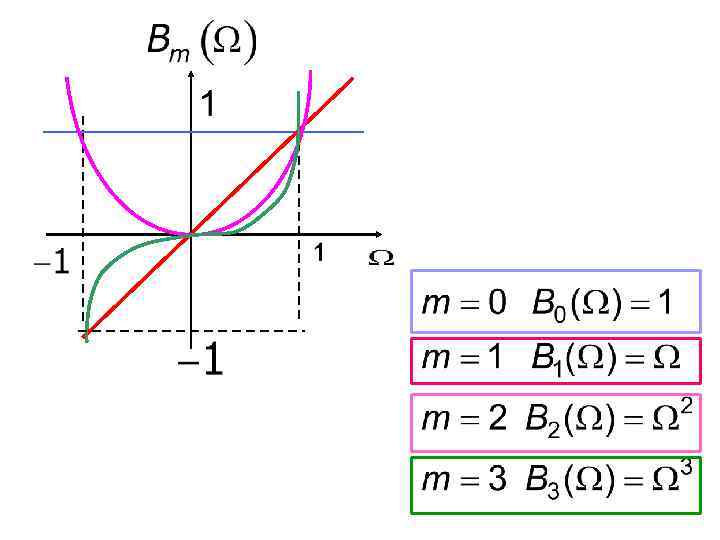
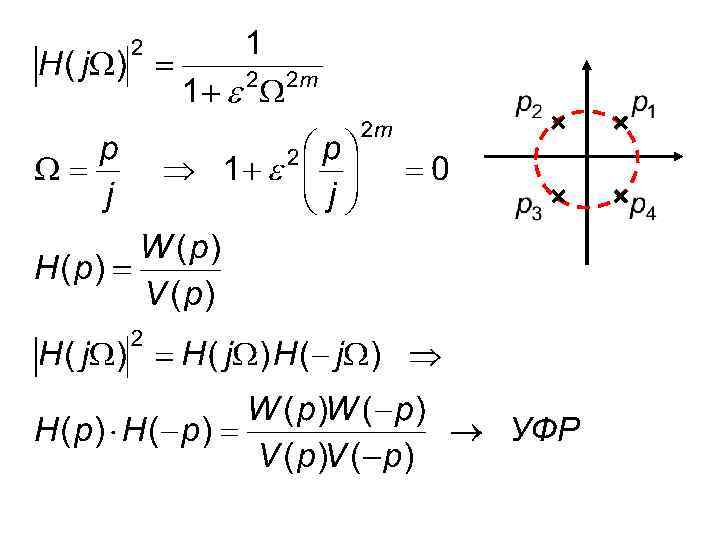
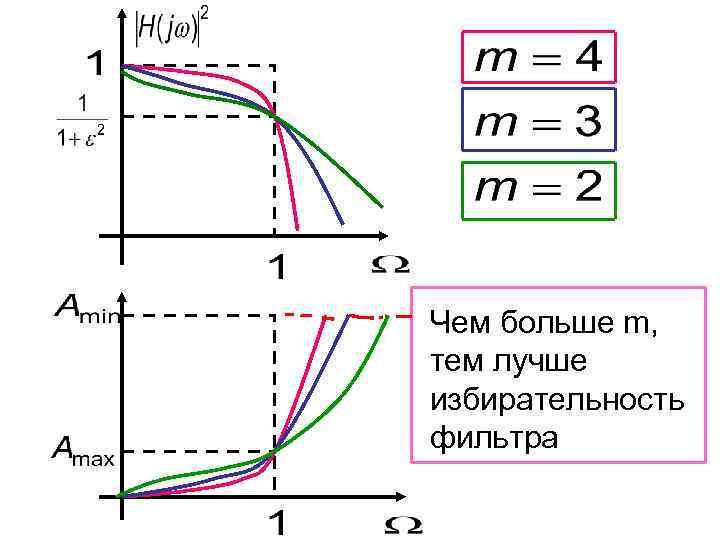Чем больше m, тем лучше избирательность фильтра

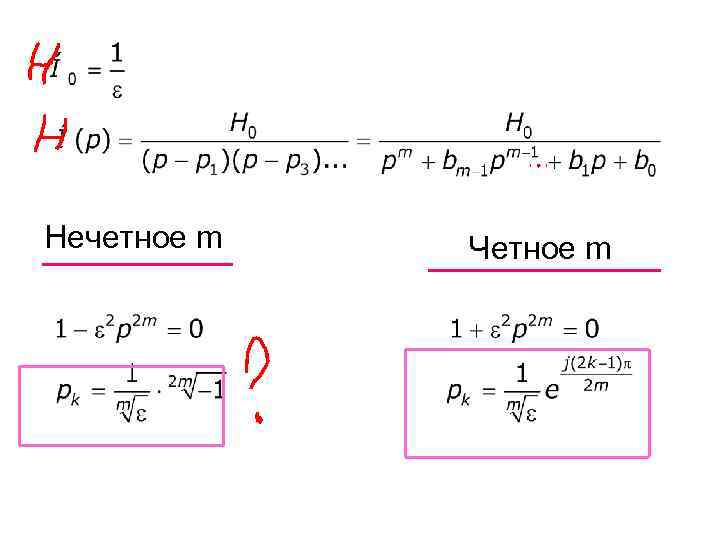Нечетное m Четное m

17. 5 Фильтры Чебышева

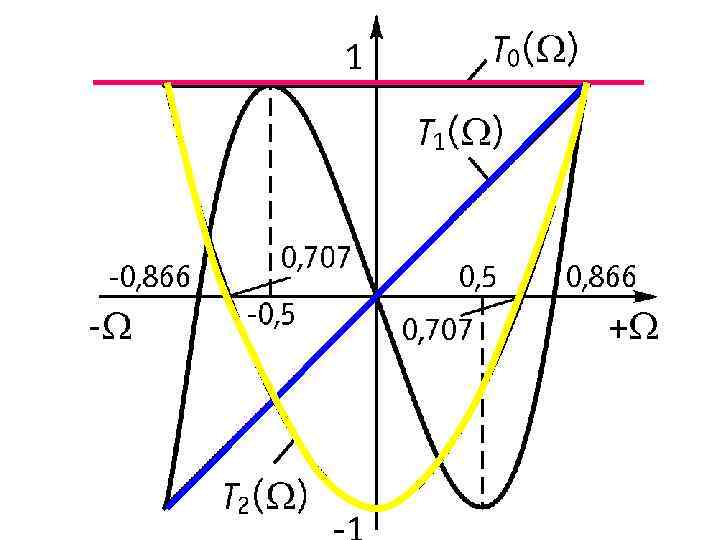
Кол-во экстремумов - m+1 Кол-во пересечений с осью Х - m При Ω>1 возрастает Скорость нарастания значения полинома тем выше, чем больше его степень

Для того, чтобы аппроксимировать заданную характеристику ослабления необходимо подобрать степень полинома Чебышева и найти ε.

При Ω=1 определяется ε (граница ПП) коэф-т неравномерности в ПП m - целое число

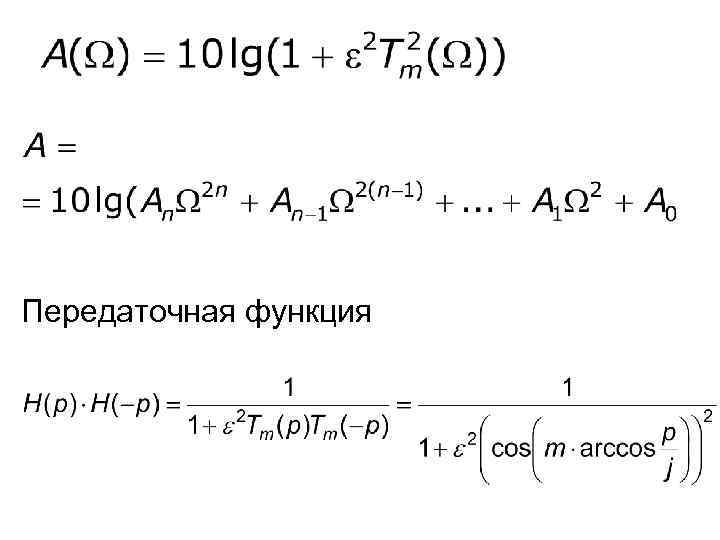Передаточная функция

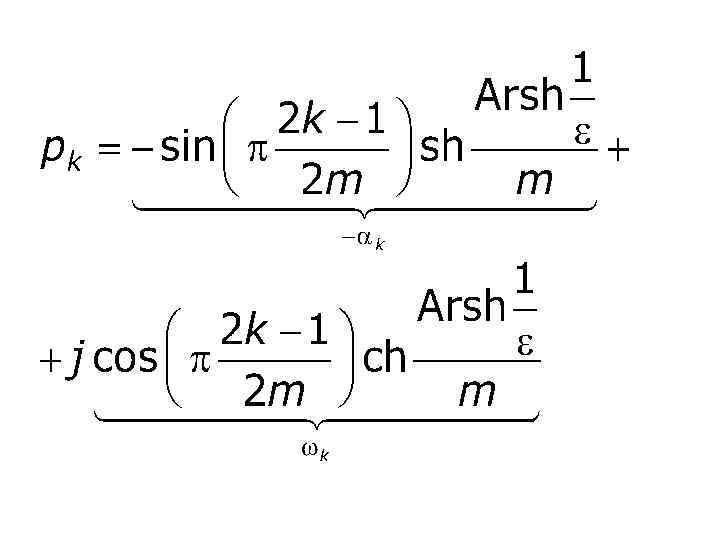
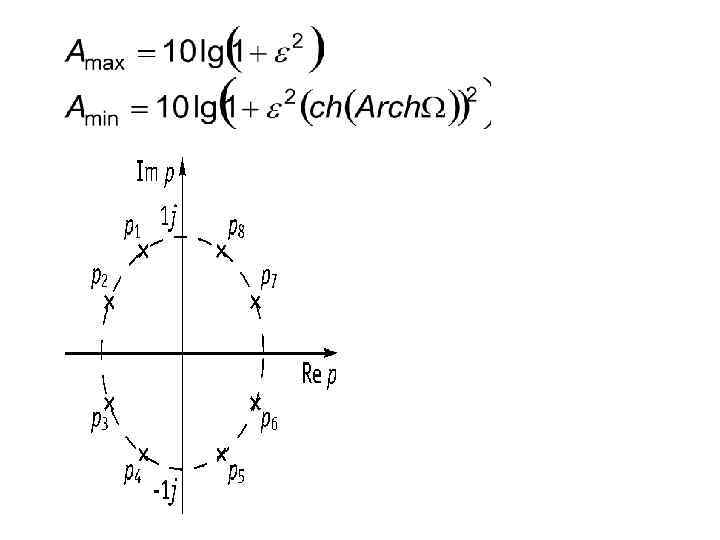
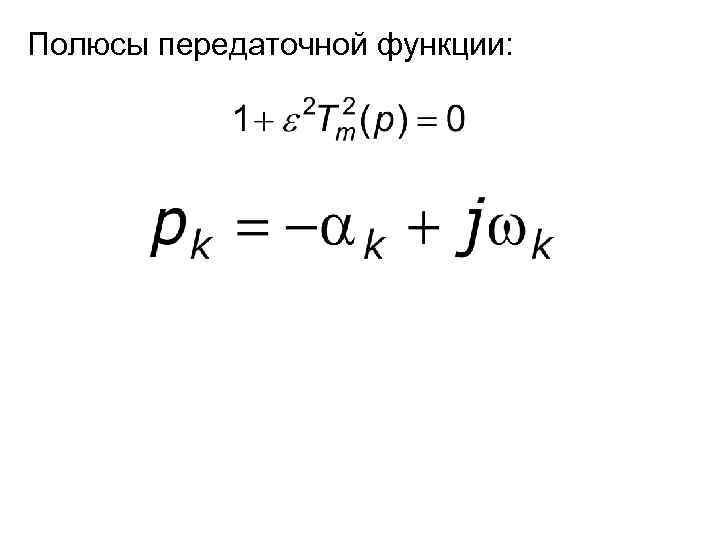Полюсы передаточной функции:

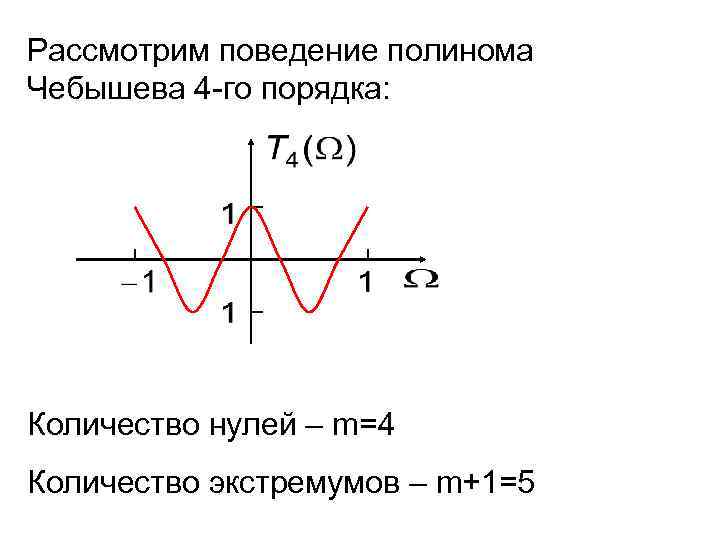Рассмотрим поведение полинома Чебышева 4 -го порядка: Количество нулей – m=4 Количество экстремумов – m+1=5

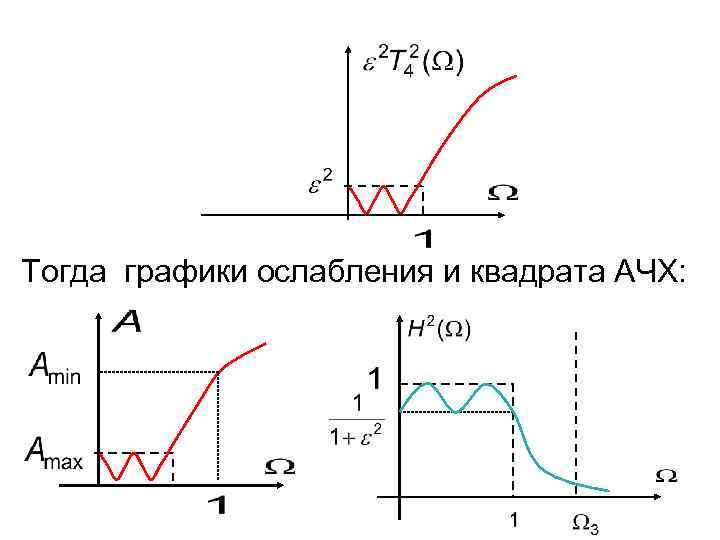Тогда графики ослабления и квадрата АЧХ:

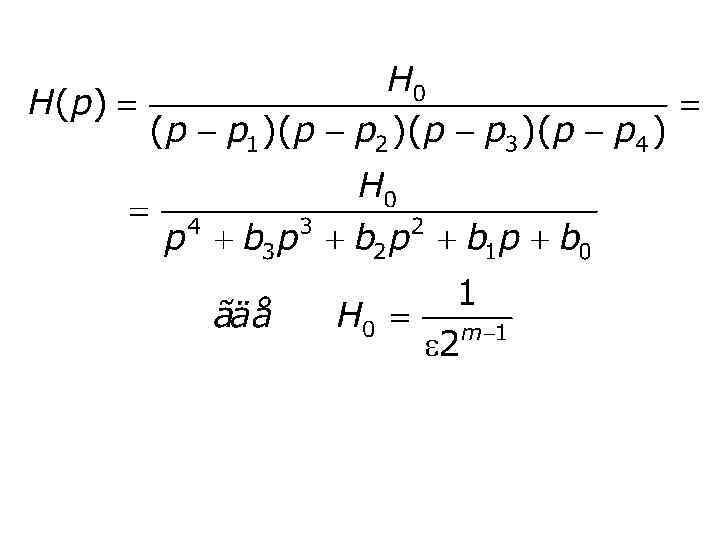
Сравнительная характеристика фильтров Баттерворта и Чебышева 1. Фильтры Чебышева имеют максимальную крутизну характеристики при одинаковых требованиях среди всех полиномиальных фильтров (выше избирательность). 2. Фильтры Баттерворта меньше искажают сигнал (АЧ и ФЧ искажения) благодаря монотонной характеристики в ПП