XVII Дискретные цепи и сигналы 8 1

XVII Дискретные цепи и сигналы

8. 1 Дискретные сигналы

• Аналоговый сигнал – непрерывная или кусочно-непрерывная функция x(t) • Дискретный сигнал (ДС) – последовательность отсчетов функции x(t), взятых в определенные моменты времени: 0 Т, 1 Т, 2 Т, …, n. Т, где Т – интервал времени, через который берутся отсчеты (интервал дискретизации)

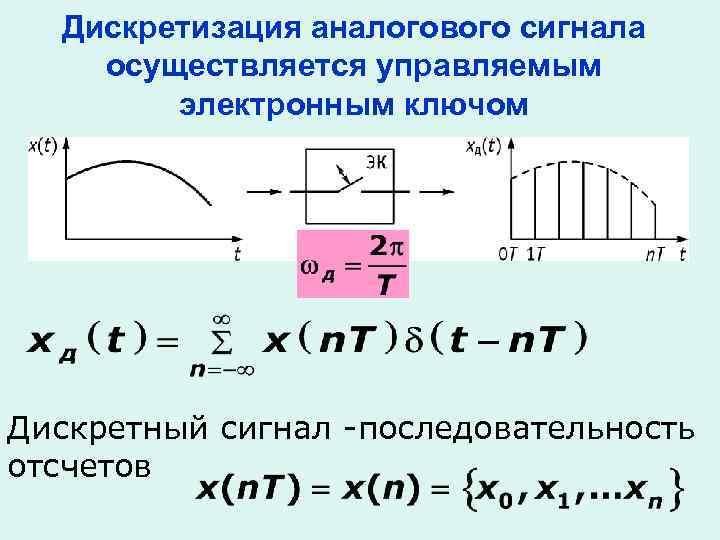Дискретизация аналогового сигнала осуществляется управляемым электронным ключом Дискретный сигнал -последовательность отсчетов

Преобразование Фурье позволяет определить спектр дискретного сигнала по последовательности его отсчетов

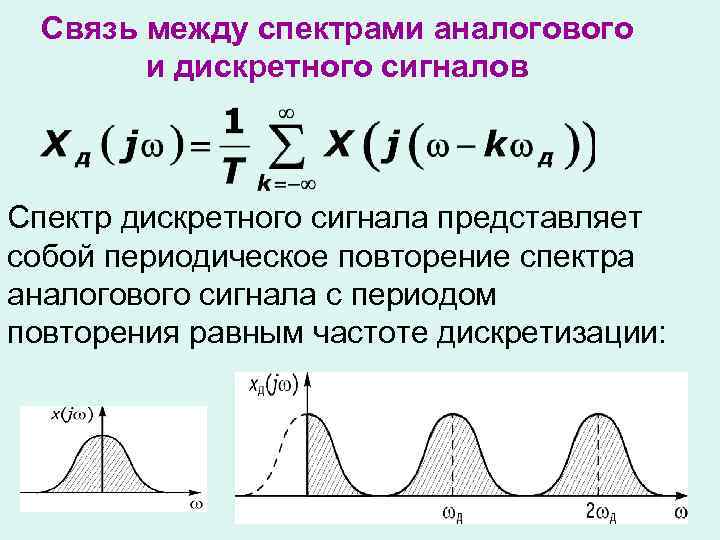Связь между спектрами аналогового и дискретного сигналов Спектр дискретного сигнала представляет собой периодическое повторение спектра аналогового сигнала с периодом повторения равным частоте дискретизации:

Теорема Котельникова Аналоговый сигнал с конечным спектром полностью определяется последовательностью своих отсчетов, взятых с интервалом , где - верхняя частота спектра аналогового сигнала

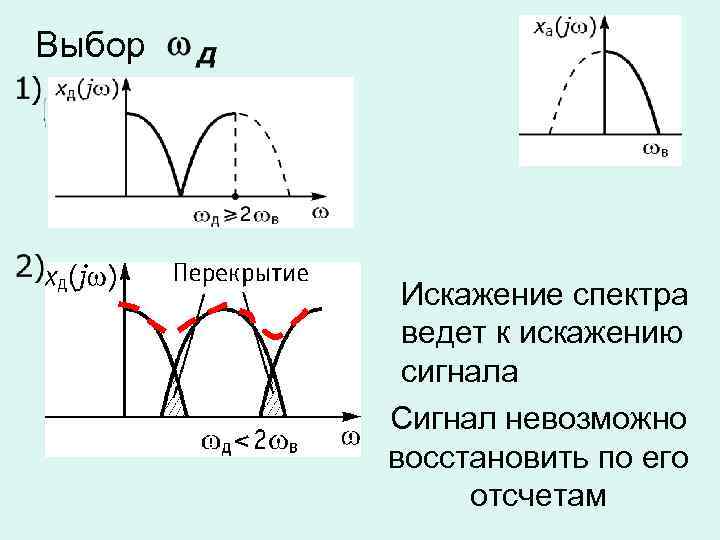Выбор Искажение спектра ведет к искажению сигнала Сигнал невозможно восстановить по его отсчетам

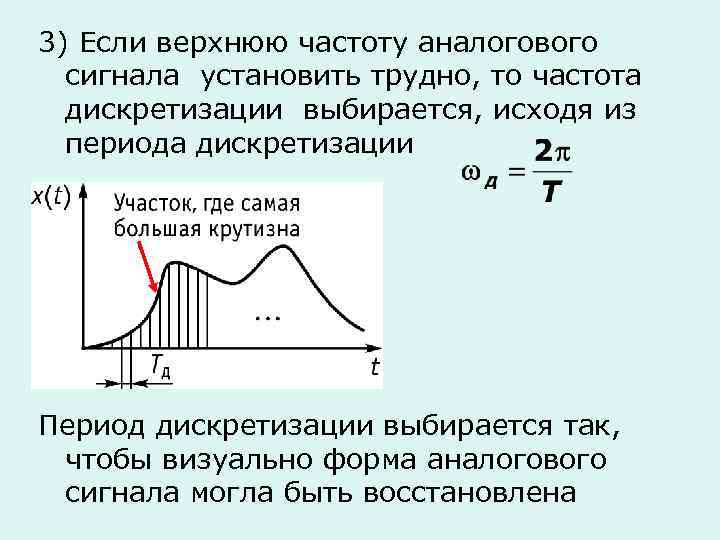3) Если верхнюю частоту аналогового сигнала установить трудно, то частота дискретизации выбирается, исходя из периода дискретизации Период дискретизации выбирается так, чтобы визуально форма аналогового сигнала могла быть восстановлена

8. 2 Прямое и обратное дискретные преобразования Фурье

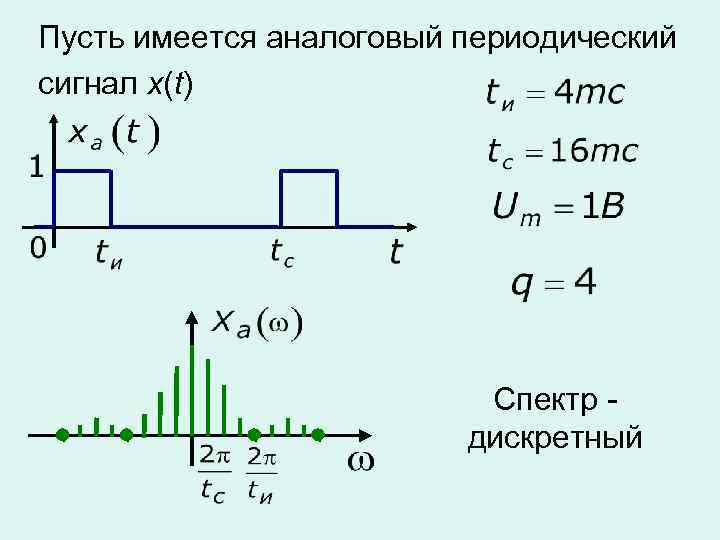Пусть имеется аналоговый периодический сигнал x(t) Спектр дискретный

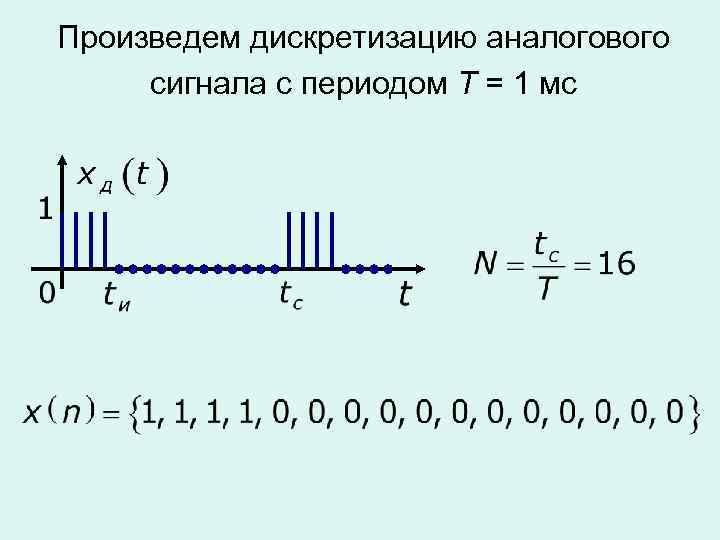Произведем дискретизацию аналогового сигнала с периодом T = 1 мс

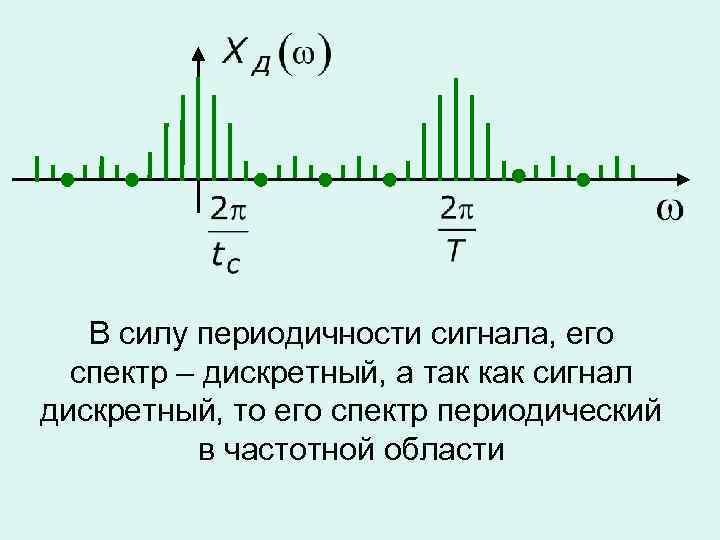В силу периодичности сигнала, его спектр – дискретный, а так как сигнал дискретный, то его спектр периодический в частотной области

Дискретное преобразование Фурье (ДПФ) для дискретного периодического сигнала, имеющего периодический дискретный спектр Число отсчетов сигнала и число отсчетов его спектра одинаковы на периоде повторения

ДПФ применяют для периодических сигналов Огибающая спектра периодического дискретного сигнала совпадает со спектром дискретного непериодического сигнала. Можно определить спектр непериодического сигнала, используя ДПФ, для этого необходимо сделать его периодическим

Пример Применить прямое ДПФ к сигналу и ОДПФ к полученным коэффициентам ДПФ Делаем сигнал периодическим

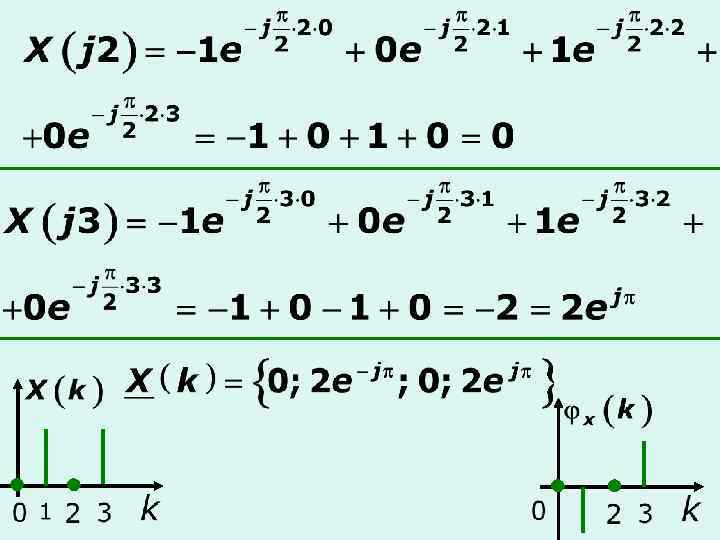
Рассчитаем отсчеты по найденным коэффициентам ДПФ с помощью формулы ОДПФ

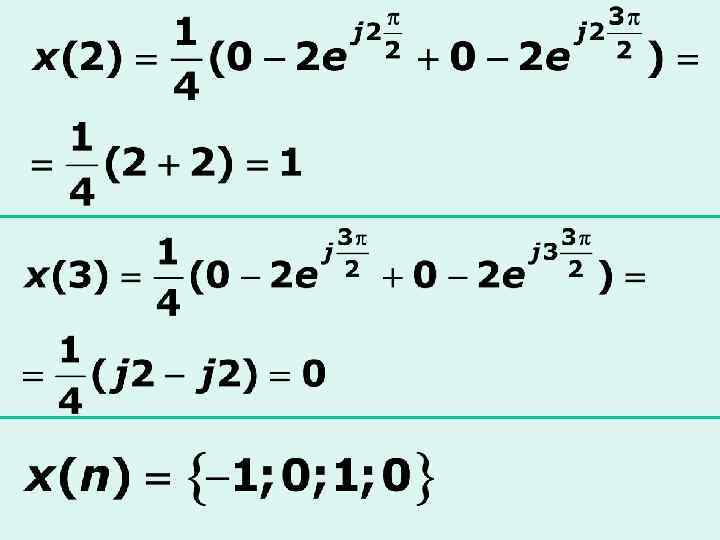
8. 3 Z-преобразование дискретных сигналов

Z-преобразование в цифровой обработке сигналов играет такую же роль, как и преобразование Лапласа при анализе аналоговых цепей и сигналов дискретный сигнал его Zизображение

Свойства Z-преобразования 1. Свойство однозначности: каждой последовательности соответствует одно и только одно zпреобразование. 2. Линейность:

3. Теорема запаздывания: если , тогда 4. Теорема свертки: свертка сигналов соответствует умножению их zпреобразований

Пример Выполнить линейную свертку входного сигнала и импульсной характеристики Решение длина выходной последовательности - длина входной последовательности - длина импульсной характеристики

5. Теорема умножения сигналов: умножение сигналов соответствует свертке z-преобразований сигналов 6. Теорема Парсеваля

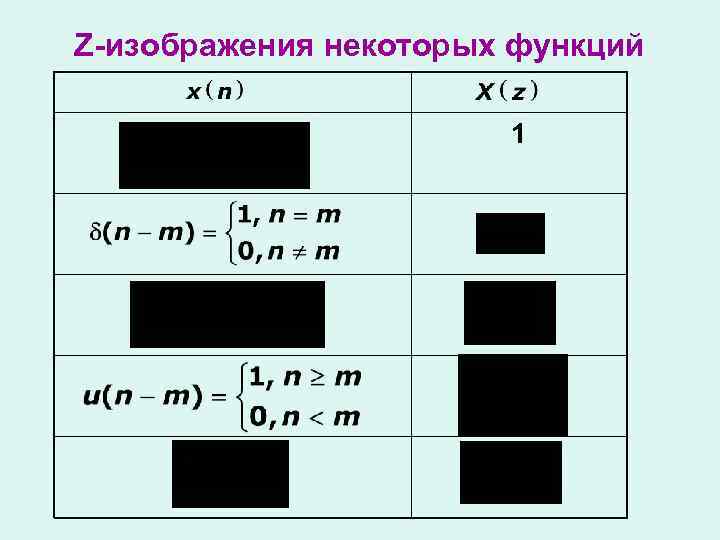Z-изображения некоторых функций 1

Методы определения сигналов по его z-изображению 1. С помощью теоремы вычетов 2. Разложение функции на простые дроби 3. Метод непрерывного деления полинома числителя на полином знаменателя

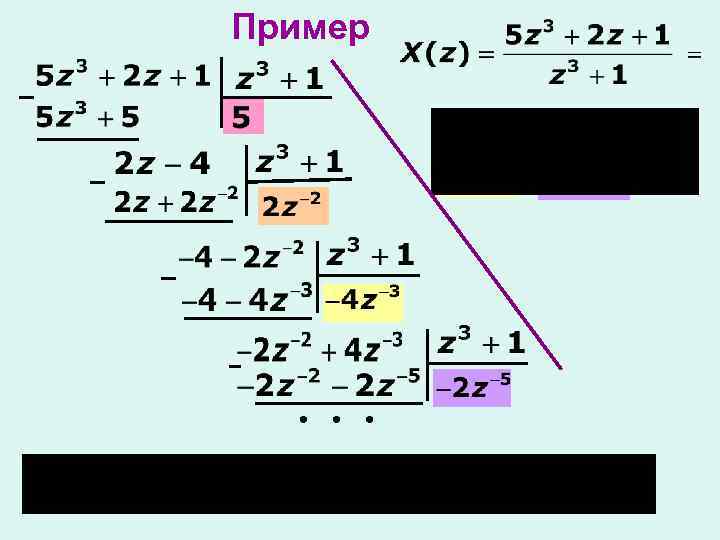Пример

Связь между Zпреобразованием и преобразованиями Лапласа и Фурье

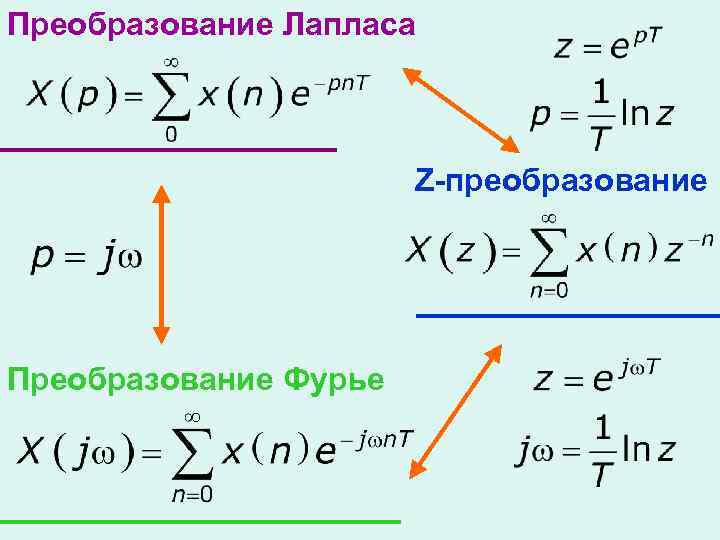Преобразование Лапласа Z-преобразование Преобразование Фурье

Преобразование точек р плоскости в точки Z-плоскости - комплексное число При движении точки на плоскости Р вдоль оси , т. е. при , соответствующая ей точка плоскости Z описывает окружность единичного радиуса

Один полный оборот радиус-вектора соответствует изменению частоты При движении точки р1 вдоль оси в пределах от до точка z 1 описывает бесконечное число окружностей

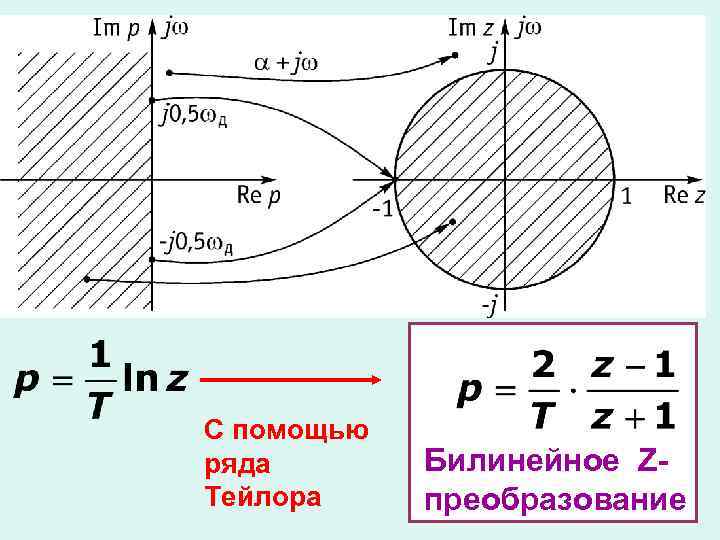С помощью ряда Тейлора Билинейное Zпреобразование

• Взаимно-однозначное отображение p на z существует только для полосы р - плоскости в пределах . Внутри этой полосы левая полуплоскость отображается внутрь единичного круга, правая – во всю zплоскость, исключая единичной круг • Все параллельные полосы р-плоскости такой же ширины также отображаются на всю z-плоскость.

8. 4 Дискретные цепи. Разностные уравнения дискретных цепей

• Дискретная цепь (ДЦ) – любая система (цепь), преобразующая одну последовательность х(n) в другую последовательность y(n). • Свойство линейности ДЦ– выходная реакция на сумму дискретных сигналов равна сумме реакций на эти сигналы. • Свойство стационарности ДЦ – задержка входного дискретного сигнала приводит лишь к такой же задержке выходного дискретного сигнала.

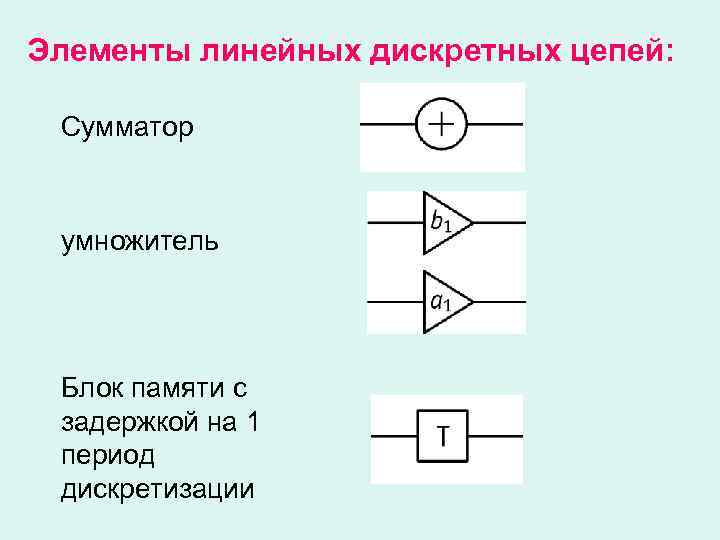Элементы линейных дискретных цепей: Сумматор умножитель Блок памяти с задержкой на 1 период дискретизации

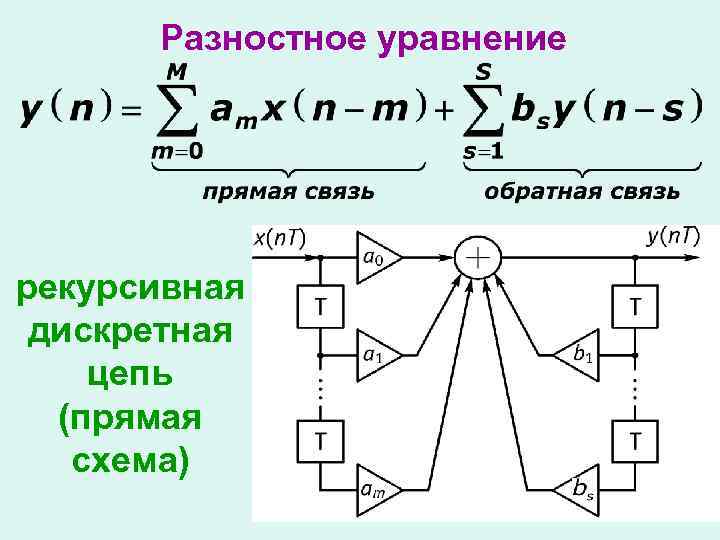Разностное уравнение рекурсивная дискретная цепь (прямая схема)

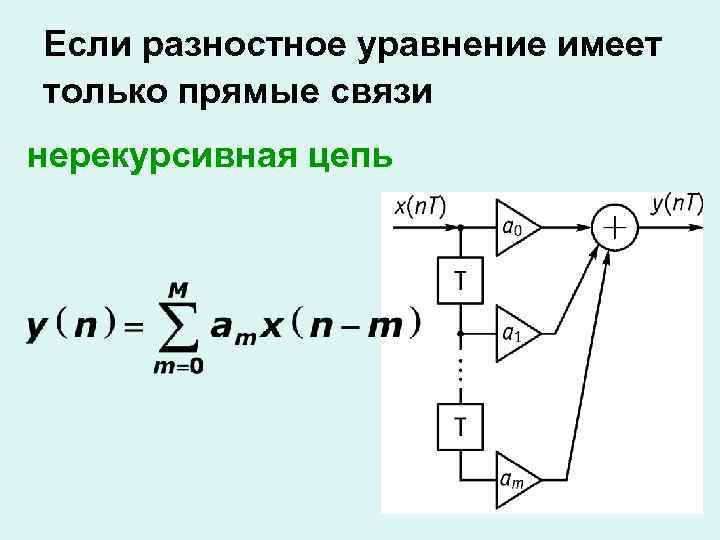Если разностное уравнение имеет только прямые связи нерекурсивная цепь

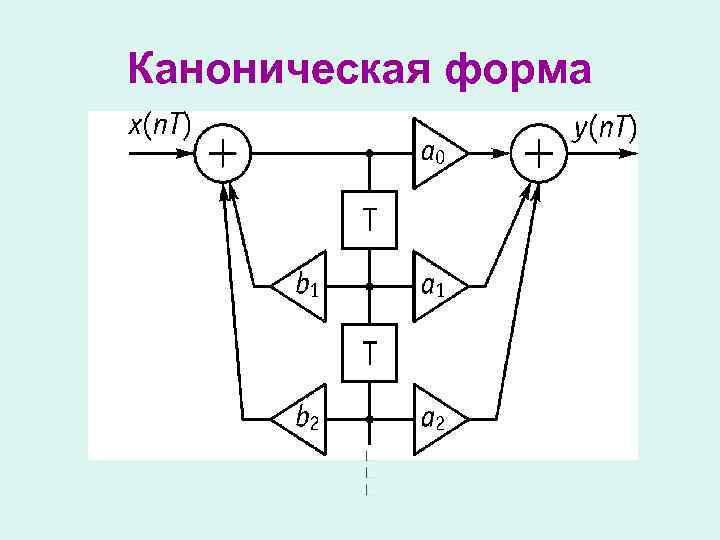Каноническая форма

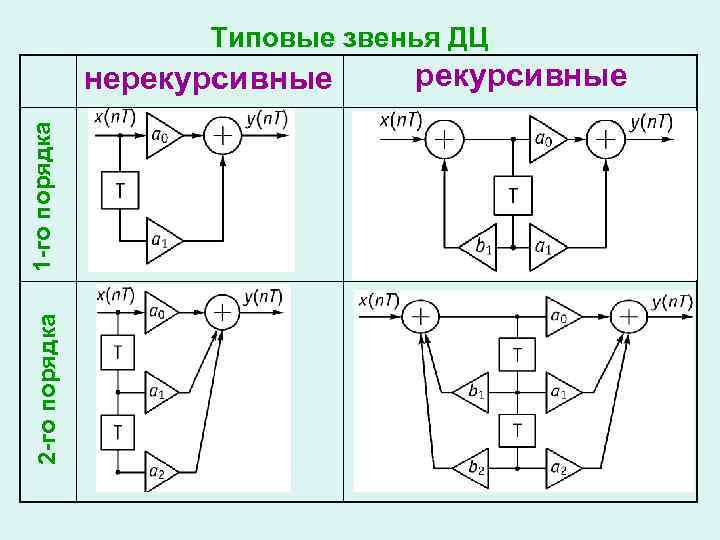Типовые звенья ДЦ 2 -го порядка 1 -го порядка нерекурсивные

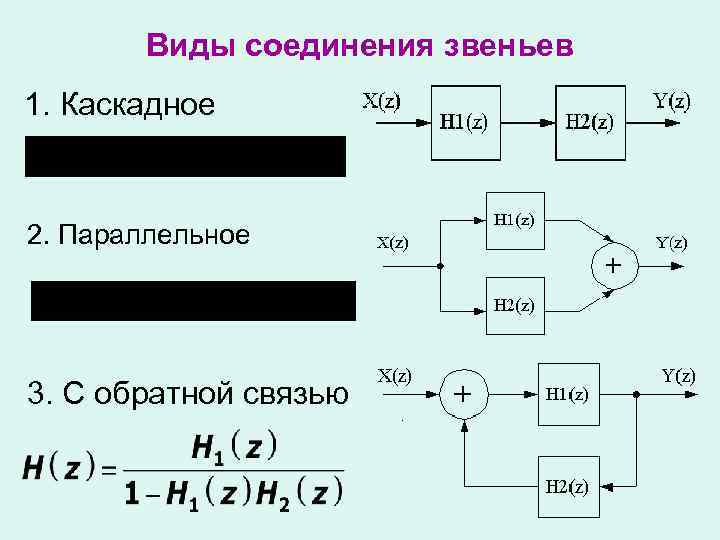Виды соединения звеньев 1. Каскадное 2. Параллельное 3. С обратной связью

8. 5 Системные характеристики дискретных цепей

Передаточная функция рекурсивной цепи нерекурсивной цепи Передаточная функция может быть получена путем Z-преобразования разностного уравнения

Комплексная частотная характеристика Частотные характеристики ДЦ – периодические функции с периодом, равным частоте дискретизации

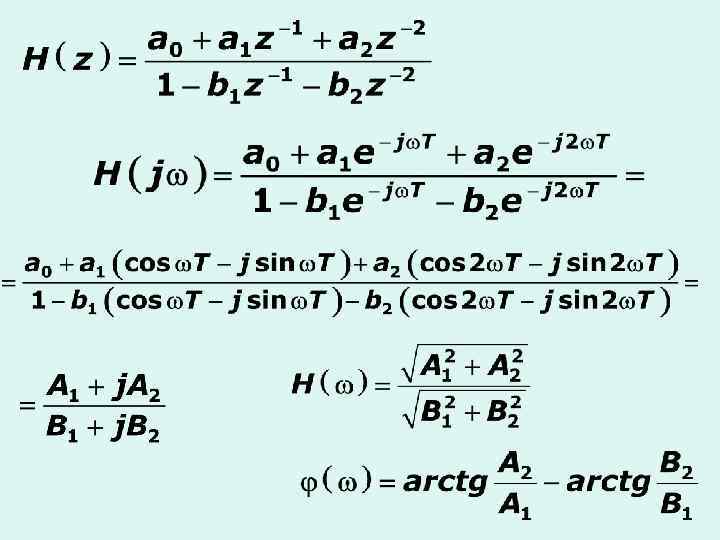
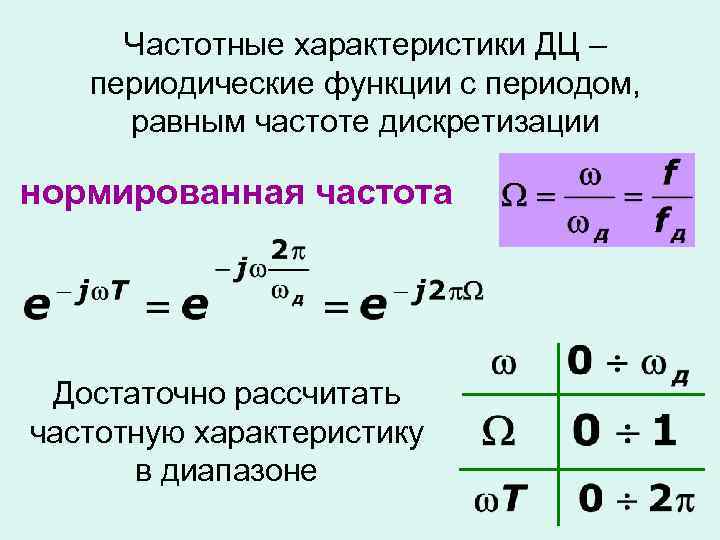Частотные характеристики ДЦ – периодические функции с периодом, равным частоте дискретизации нормированная частота Достаточно рассчитать частотную характеристику в диапазоне

Пример рассчитать комплексную частотную характеристику

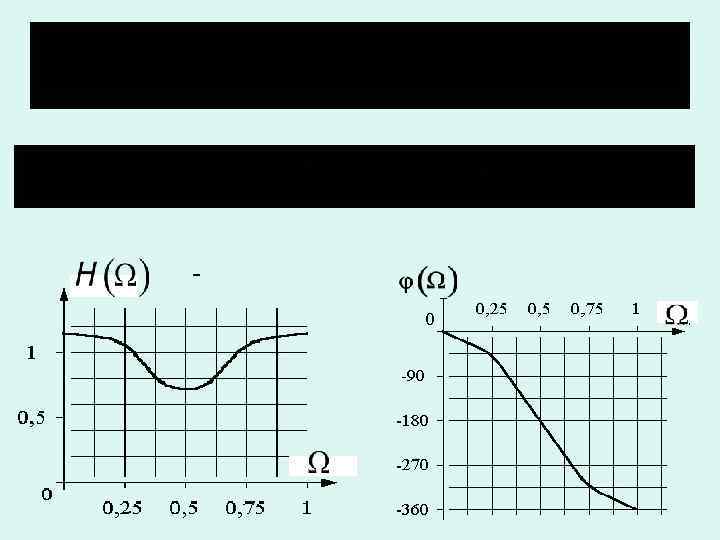
Устойчивость ДЦ Если полюсы передаточной функции цепи H(z) находятся внутри окружности единичного радиуса на комплексной плоскости z, то цепь устойчива

Импульсная характеристика дискретной цепи h(n) – реакция дискретной цепи на сигнал в виде дискретной δ-функции при

Способы определения импульсной характеристики 1. По разностному уравнению Пример

2. Выполнив обратное Z-преобразование H(z) Пример

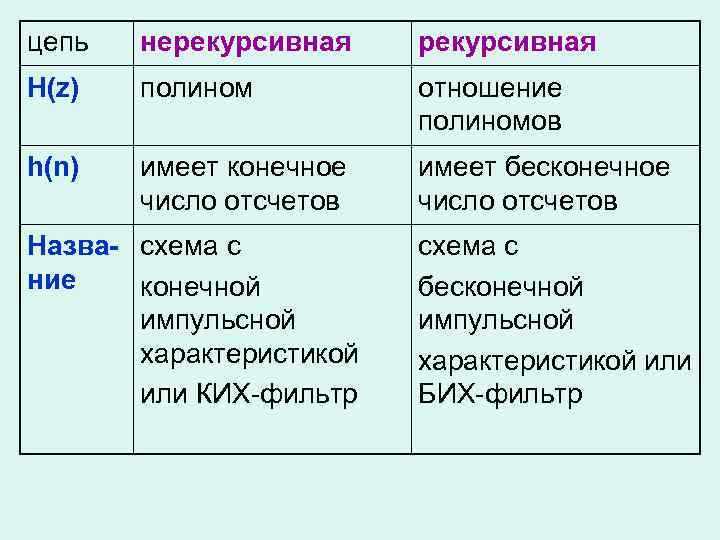цепь нерекурсивная H(z) полином отношение полиномов h(n) имеет конечное число отсчетов имеет бесконечное число отсчетов Назва- схема с ние конечной импульсной характеристикой или КИХ-фильтр схема с бесконечной импульсной характеристикой или БИХ-фильтр

Определение сигнала на выходе ДЦ 1. По разностному уравнению 2. Выполнив свертку последовательностей x(n) и h(n) 3. Определив и выполнив обратное Z-преобразование 4. Определив . Для расчетов можно применять ДПФ и ОДПФ.