ХV международный научный семинар Высокие технологии в машиностроении

ХV международный научный семинар "Высокие технологии в машиностроении" INTERPARTNER – 2006 11 – 16 сентября 2006 года ТЕРМОМЕХАНИЧЕСКАЯ КОНЕЧНО-ЭЛЕМЕНТНАЯ МОДЕЛЬ ПРОЦЕССА РЕЗАНИЯ СТАЛЕЙ Докладчик: Криворучко Дмитрий Владимирович Сумский государственный университет Харьков-Алушта - 2006

Структура доклада Исторический обзор n Расчетная схема, общий алгоритм n Особенности используемого математического аппарата n Программная реализация n Пример расчета и анализ результатов n Экспериментальная проверка n Перспективы развития n

Исторический обзор n n Развитие подхода с 1971 года Наиболее известные школы: зарубежные: проф. Usui E. , проф. Altan T. , проф. Marusich T. , проф. Strenkovski S. и др. отечественные: проф. Остафьев В. А.

Цель исследования: создание прогнозирующей конечно-элементной модели процесса прямоугольного свободного резания, адекватной в широком диапазоне условий резания

Задачи исследования. 1. Совершенствование математического аппарата так, что можно было учесть: Ø Ø большие и локализованные пластические деформации; сложные свойства обрабатываемого материала, определяемые деформацией, скоростью деформации и температурой. контактное взаимодействие и трение, определяемое тепловым состоянием в контакте; образование трещины и формирование стружки. 2. Разработка программного обеспечения. 3. Выполнение экспериментальной проверки.

Расчетная схема

Общий алгоритм

Особенности используемого математического аппарата n Схема интегрирования уравнения динамики по времени - ЯВНАЯ

Особенности используемого математического аппарата

Особенности используемого математического аппарата Кривые течения стали 45 s, МПа E-Magd E. , Treppman C. Mechanical behaviour of AA 7075, Ck 45 N and Ti. Al 6 V 4 at high strain rates//Materialsweek. -2000.

Особенности используемого математического аппарата Реологическая модель (уравнение состояния) Механическая модель – уравнение в форме Джонсона-Кука с учетом адиабатического разогрева Термомеханическая модель – уравнение упруго-пластической среды с линейным упрочнением с поправкой Cowper-Symond на скорость деформации

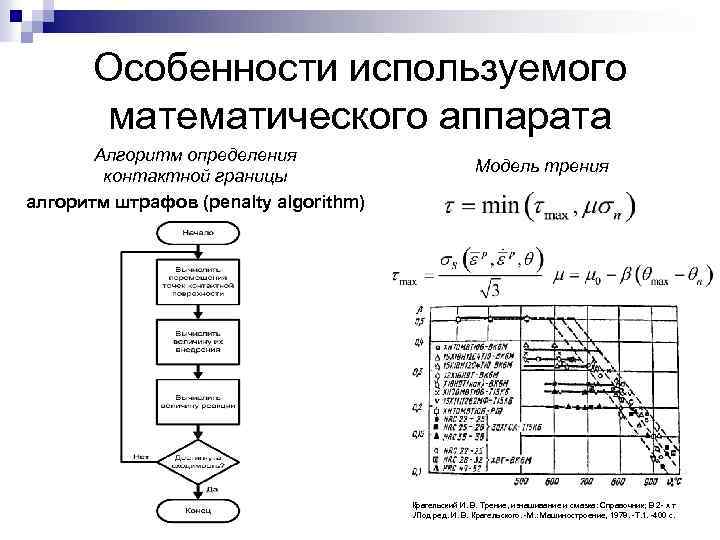Особенности используемого математического аппарата Алгоритм определения контактной границы алгоритм штрафов (penalty algorithm) Модель трения Крагельский И. В. Трение, изнашивание и смазка: Справочник; В 2 - х т. /Под ред. И. В. Крагельского. -М. : Машиностроение, 1978. -Т. 1. -400 c.

Общий алгоритм Уравнение теплопроводности

Особенности используемого математического аппарата Особенности решения По Миллеру А. Д. Sekhon, G. S. and Chenot, J. L. , Numerical Simulation of Continuous Chip Formation During Non-Steady Orthogonal Cutting, " Engineering Computations, 10 (1993) 31 -48.

Особенности используемого математического аппарата Конечно-элементная сетка Конечные элементы - четырехугольные: - билинейная интерполяция перемещений; - численная устойчивость; - минимальное количество элементов. Система координат - Лагранжиева Устранение искажений КЭ элементов: - ALE-технология; - перестроение сетки. Генератор КЭ сетки – алгоритм Q-morph (advanced front)

Особенности используемого математического аппарата n Требования к КЭ сетке - Минимальное количество элементов; - Сгущение в области больших деформаций; - Отсутствие треугольников; - Минимальный угол четырехугольника 60 ; - Отсутствие в одной области элементов, существенно отличающихся по размерам;

Особенности используемого математического аппарата Удаление конечных элементов, в которых выполняется условие физический критерий разрушения Перестроение КЭ сетки через заданный период времени - геометрический критерий разрушения

Программная реализация OCFEM + LS-DYNA

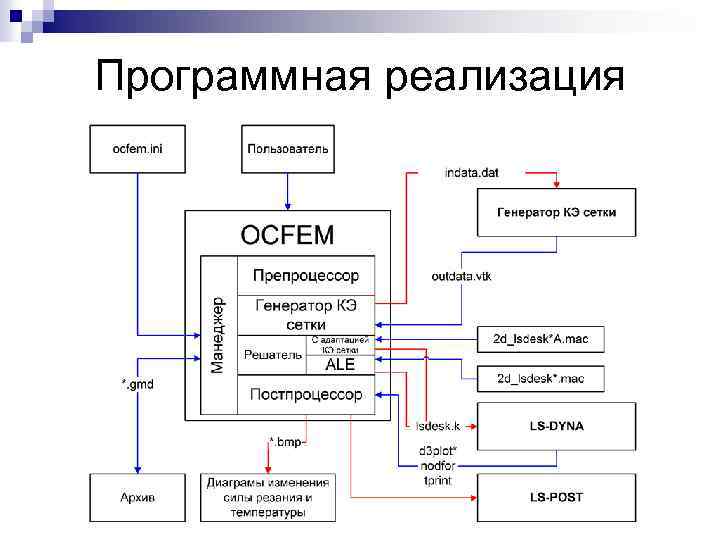Программная реализация

Программная реализация

Пример расчета и анализ результатов n Инструментальный материал - твердый сплав Т 15 К 6 Механические свойства инструментального материала: E=580 ГПа, =0. 3, = 11200 кг/м 3. n Обрабатываемый материал - сталь 45 (НВ 196± 5) Механические свойства обрабатываемого материала: E=200 ГПа, =0. 3, = 7850 кг/м 3 n Параметры модели трения: n Сухое резание. Коэффициент теплоотдачи:

Пример моделирования и анализ результатов СТАЛЬ 45 – Т 15 К 6, V=150 м/мин, S=0, 1 мм/об, γ=10°, α=10°, ρ=0, 02 мм, hz=0 мм Температура Максимальные касательные напряжения C ГПа Интенсивность скорости пластической деформации Интенсивность пластической деформации 1/мс

Пример результатов расчета и анализ результатов t=1 мс СТАЛЬ 45 – Т 15 К 6, V=150 м/мин, S=0, 1 мм/об, γ=10°, α=10°, ρ=0, 02 мм, hz=0 мм 20 Температура, С Интенсивность скорости пластической деформации, 1/мс 467 20 68 188 Максимальные касательные напряжения, ГПа Интенсивность пластической деформации 0, 00 0, 63 3. 7

Пример результатов расчета и анализ результатов Изменение показателей процесса во времени СТАЛЬ 45 – Т 15 К 6, V=150 м/мин, S=0, 1 мм/об, γ=10°, α=10°, ρ=0, 02 мм, hz=0 мм

Пример расчета и анализ результатов n Влияние скорости резания СТАЛЬ 45 – Т 15 К 6, S=0, 1 мм/об, γ=10°, α=10°, ρ=0, 02 мм, hz=0 мм

Пример расчета и анализ результатов n Влияние подачи СТАЛЬ 45 – Т 15 К 6, V=150 м/мин, γ=10°, α=10°, ρ=0, 02 мм, hz=0 мм

Пример расчета и анализ результатов Влияние коэффициента трения n T, C 700 600 500 400 300 200 100 0 0 0, 2 0, 4 0, 6 0, 8 Сталь 45, = 5 , V = 300 м/мин, a= 0, 150 мм

Экспериментальная проверка По данным Ivester R. W. , Kennedy M. , Davies M. A. Assessment of Machining Models: Progress Report//www. mel. nist. gov/div 822/amm. -Gaithersburg: National Institute of Standart and Metrology, 2000. 500 Н Значение показателя 294 Н 650 С 2, 2 1, 9 420 Н 580 С Значение показателя из эксперимента % 80 Н

Перспективы развития Совершенствование критерия разрушения и алгоритма моделирования трещинообразования n Разработка методики экспериментального определения параметров реологической модели обрабатываемого материала n Реализация 3 D решения n

СПАСИБО ЗА ВНИМАНИЕ!