XML Constraints Wenfei Fan University of Edinburgh and

XML Constraints Wenfei Fan University of Edinburgh and Bell Laboratories 1

Outline of Part IV ü XML Specifications: types and integrity constraints ü Specification of XML constraints: – keys, foreign keys, FDs – absolute vs. relative constraints ü Analysis of XML constraints – Consistency analysis – Implication analysis ü Applications of XML constraints, and research issues – Relational storage of XML data via constraint propagation – Schema-directed XML integration – Normal forms, query optimization, updates, data cleaning. . . 2

Introduction to XML specificaiton ü XML Specification: – types – integrity constraints – the need for XML constraints 3

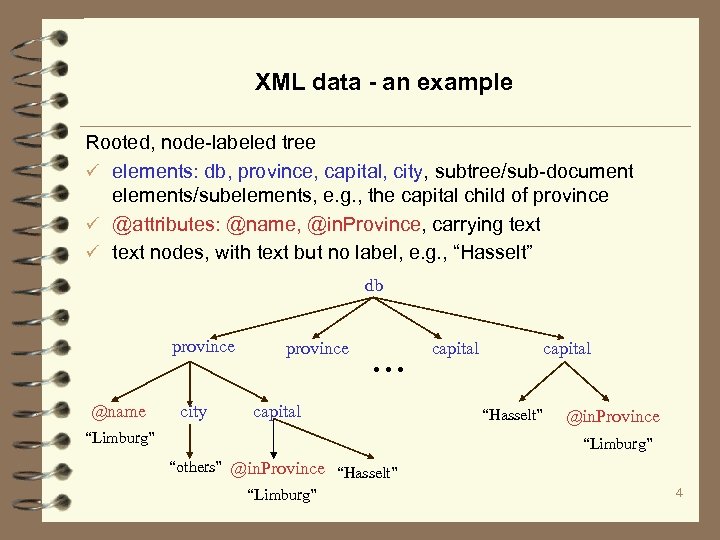
XML data - an example Rooted, node-labeled tree ü elements: db, province, capital, city, subtree/sub-document elements/subelements, e. g. , the capital child of province ü @attributes: @name, @in. Province, carrying text ü text nodes, with text but no label, e. g. , “Hasselt” db province @name city province . . . capital “Limburg” capital “Hasselt” @in. Province “Limburg” “others” @in. Province “Hasselt” “Limburg” 4

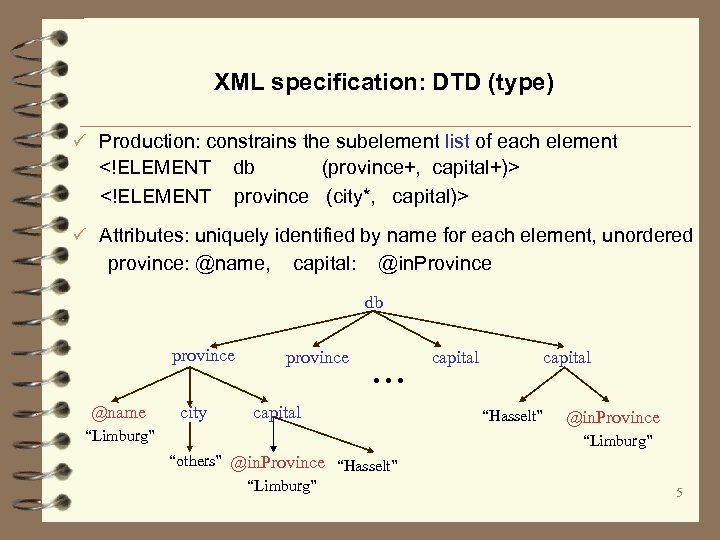
XML specification: DTD (type) ü Production: constrains the subelement list of each element <!ELEMENT db (province+, capital+)> province (city*, capital)> ü Attributes: uniquely identified by name for each element, unordered province: @name, capital: @in. Province db province @name city province . . . capital “Limburg” capital “Hasselt” @in. Province “Limburg” “others” @in. Province “Hasselt” “Limburg” 5

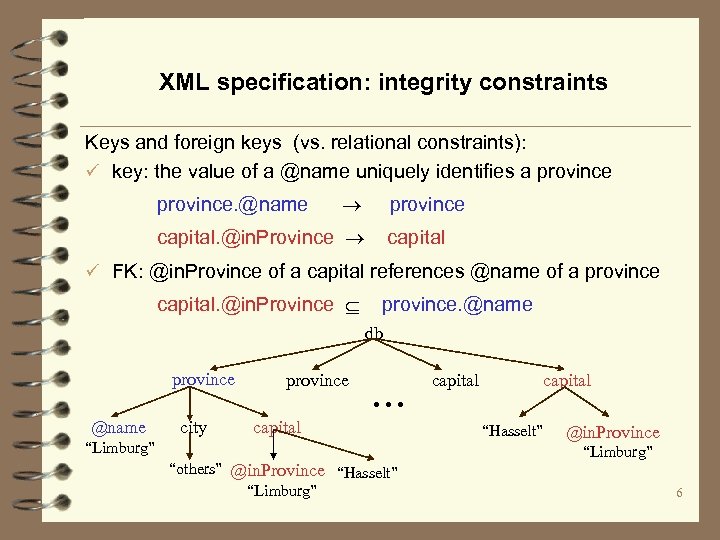
XML specification: integrity constraints Keys and foreign keys (vs. relational constraints): ü key: the value of a @name uniquely identifies a province. @name province capital. @in. Province capital ü FK: @in. Province of a capital references @name of a province capital. @in. Province province. @name db province @name city province . . . capital “Limburg” “others” @in. Province “Hasselt” “Limburg” capital “Hasselt” @in. Province “Limburg” 6

XML specification ü A type (DTD) D ü A set of integrity constraints, Example: ü DTD D: structure of the document, vs. types in a PL <!ELEMENT db (province+, capital+)> <!ELEMENT province (city*, capital)> province. @name, capital. @in. Province ü Constraints : defined in terms of data values across elements province. @name province capital. @in. Province province. @name 7

Why XML constraints? Supported by W 3 C XML standard, XML Schema In databases (supported by SQL standard), constraints are: ü an essential part of the semantics of data, ü fundamental to conceptual design, ü useful for choosing efficient storage and access methods, ü central to update anomaly prevention, ü data cleaning … In the XML setting: constraints have proved useful in ü database storage of XML data (via constraint propagation), ü schema-directed database publishing/integration in XML, ü XML query optimization and formulation, ü design theory for XML specifications: normal forms ü data cleaning, … 8

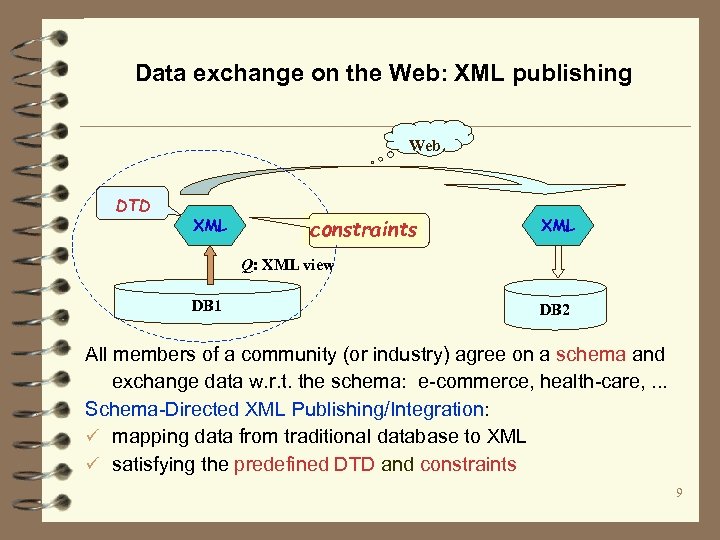
Data exchange on the Web: XML publishing Web DTD XML constraints XML Q: XML view DB 1 DB 2 All members of a community (or industry) agree on a schema and exchange data w. r. t. the schema: e-commerce, health-care, . . . Schema-Directed XML Publishing/Integration: ü mapping data from traditional database to XML ü satisfying the predefined DTD and constraints 9

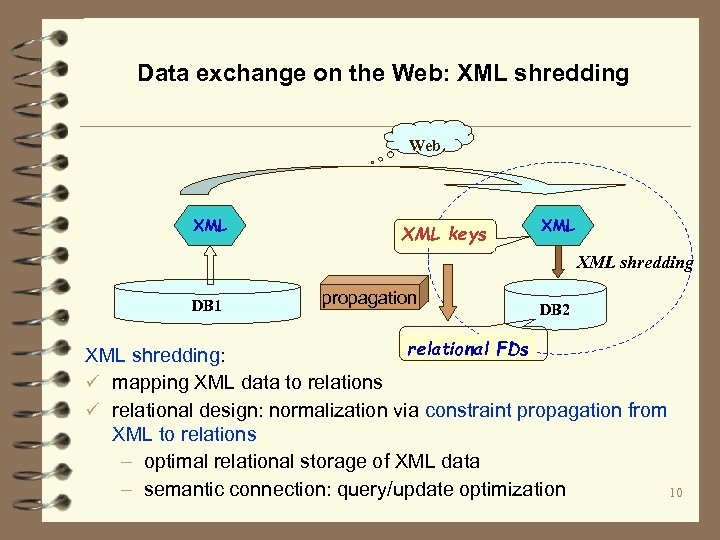
Data exchange on the Web: XML shredding Web XML keys XML shredding DB 1 propagation DB 2 relational FDs XML shredding: ü mapping XML data to relations ü relational design: normalization via constraint propagation from XML to relations – optimal relational storage of XML data – semantic connection: query/update optimization 10

XML constraints ü Specification of XML constraints: – keys, foreign keys, FDs – absolute vs. relative constraints 11

The limitations of the XML standard (DTD) <!ATTLIST country name ID <!ATTLIST province capital ID <!ATTLIST capital in. Province IDREF #required> ü Scoping: – ID unique within the entire document (like oids), while a key needs only to uniquely identify a tuple within a relation – IDREF untyped: one has no control over what it points to -you point to something, but you don’t know what it is! <student id=“ 01” name=“Saddam” taking=“qsx”/> <student id=“ 02” name=“Bush” taking=“qsx 01”/> <course id=“qsx”/> 12

The limitations of the XML standard (DTD) ü keys need to be multi-valued, while IDs must be single-valued (unary) enroll (sid: string, cid: string, grade: string) ü a relation may have multiple keys, while an element can have at most one ID (primary) ü ID/IDREF can only be defined in a DTD, while XML data may not come with a DTD/schema ü ID/IDREF, even relational keys/foreign keys, fail to capture the semantics of hierarchical data – will be seen shortly A mixture of relational keys and object identities (oids) Mild extensions of relational constraints do not work for XML! 13

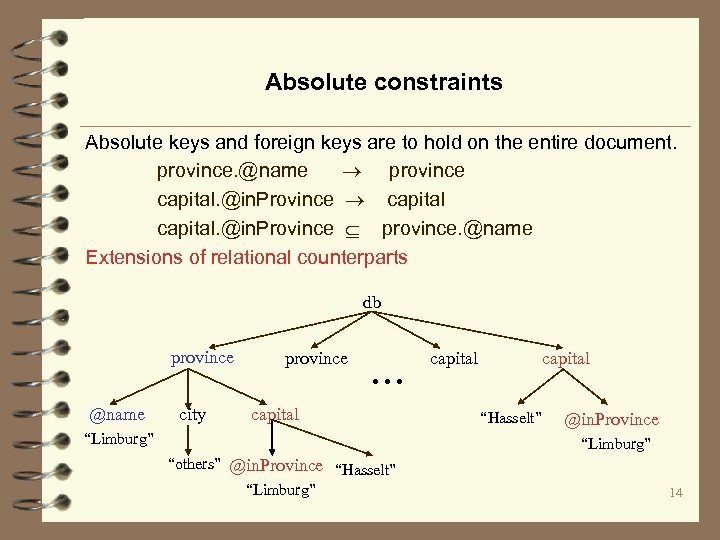
Absolute constraints Absolute keys and foreign keys are to hold on the entire document. province. @name province capital. @in. Province province. @name Extensions of relational counterparts db province @name city province . . . capital “Limburg” capital “Hasselt” @in. Province “Limburg” “others” @in. Province “Hasselt” “Limburg” 14

Absolute keys and foreign keys [PODS’ 00, 01, JACM] ü key: [X] . An XML document satisfies the key iff x y ext( ) ( l X (x. l = y. l) x = y) ü foreign key (FK): a combination of an inclusion constraint 1[X] 2[Y], and a key 2[Y] 2. A document satisfies the FK iff it satisfies the key and x ext( 1 ) y ext( 2 ) (x[X] = y[Y]) – , 1 , 2: element types; X, Y: sets (lists) of attributes; – ext( ): the set of elements in an XML document. Equality issue: ü (string) value equality: when comparing attributes ü node identify: when comparing XML elements Unary keys and foreign keys: defined in terms of single-attribute. 15

Relative constraints [WWW’ 01, PODS’ 02, SICOMP] An XML tree specifies countries, province capitals. ü What is a key for a province? ü What does @in. Province of a capital reference? db . . . country province . . . capital country province @name “Belgium” @name “Limburg” capital “Hasselt”@in. Province “Hasselt” “Limburg” @name capital “Limburg” . . . capital @name “Holland” “Maastricht” @in. Province “Limburg” @in. Province “Hasselt” “Limburg” 16

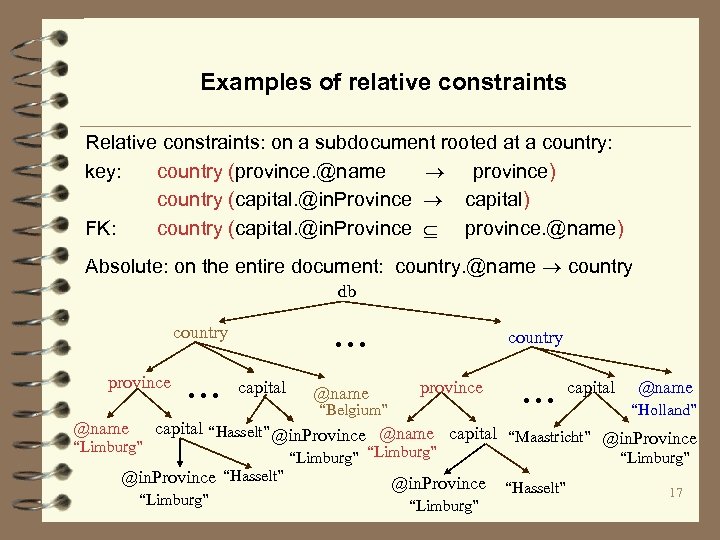
Examples of relative constraints Relative constraints: on a subdocument rooted at a country: key: country (province. @name province) country (capital. @in. Province capital) FK: country (capital. @in. Province province. @name) Absolute: on the entire document: country. @name country db . . . country province . . . capital @name country province “Belgium” . . . capital @name “Holland” capital “Hasselt” @in. Province @name capital “Maastricht” @in. Province “Limburg” @in. Province “Hasselt” “Limburg” @in. Province “Limburg” “Hasselt” 17

Relative keys and foreign keys ü key: ( 1[X] 1). An document satisfies the key iff c ext( ) y, z ext( 1) ( (y c) (z c) l X (y. l = z. l) y = z) ü foreign key (FK): ( 1[X] 2[Y] ) and a key ( 2[Y] 2). A document satisfies the FK iff it satisfies the key and c ext( ) y ext( 1) (( y c) z ext( 2 ) ((z c) y[X] = z[Y] )) where ü (y c): y is a descendant of c (y in the subtree rooted at c); ü : context type; ü ext( ): the set of elements in an XML document. 18

Relative vs. Absolute ü Absolute constraints are a special case of relative ones: country. @name country db ( country. @name country ) absolute: a fixed context type -- the root type r ü Absolute constraints are scoped within the entire document; whereas relative ones within the context of a subdocument. country (province. @name province) country (capital. @in. Province capital) country (capital. @in. Province province. @name) country. @name country Together they specify constraints on the entire document ü Beyond relational constraints; important for hierarchically structured data: XML, scientific databases, biomedical data, . . . 19

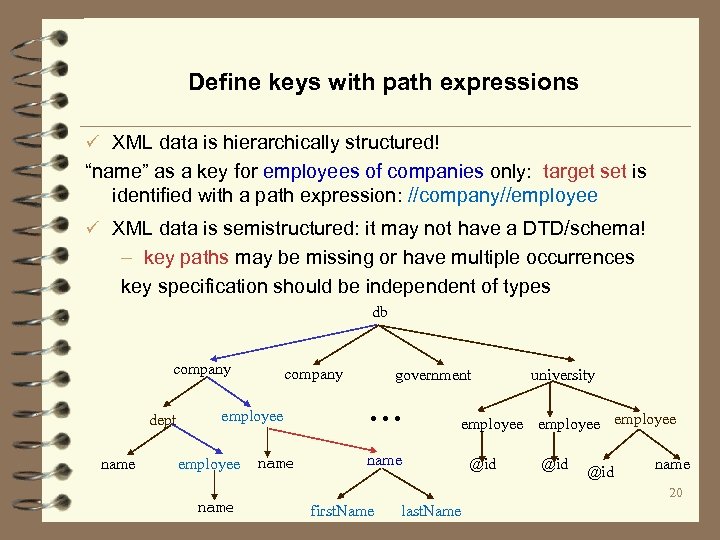
Define keys with path expressions ü XML data is hierarchically structured! “name” as a key for employees of companies only: target set is identified with a path expression: //company//employee ü XML data is semistructured: it may not have a DTD/schema! – key paths may be missing or have multiple occurrences key specification should be independent of types db company dept name company employee name government . . . university employee name @id @id name 20 first. Name last. Name

Path expressions Path expression: navigating XML trees A simple yet powerful path language: q : : = | l | q/q | // ü : empty path ü l: tag ü q/q: concatenation ü //: descendants and self – recursively descending downward 21

Absolute path constraints [WWW’ 01] Absolute key: (Q, {P 1, . . . , Pk} ) ü Path expressions Q, Pi: XPath, regular path expressions, … ü target path Q: to identify a target set [[Q]] of nodes on which the key is defined (vs. relation) ü a set of key paths {P 1, . . . , Pk}: to provide an identification for nodes in [[Q]] (vs. key attributes) ü semantics: for any two nodes in [[Q]], if they have all the key paths and agree on them by value equality (existential), then they must be the same node (value equality and node identity) Examples: (//company//employees, {name, phone}) -- composite key ( //company//employees, {//@id}) -- multiple keys (//. , {@id}) -- capturing ID attributes in DTDs 22

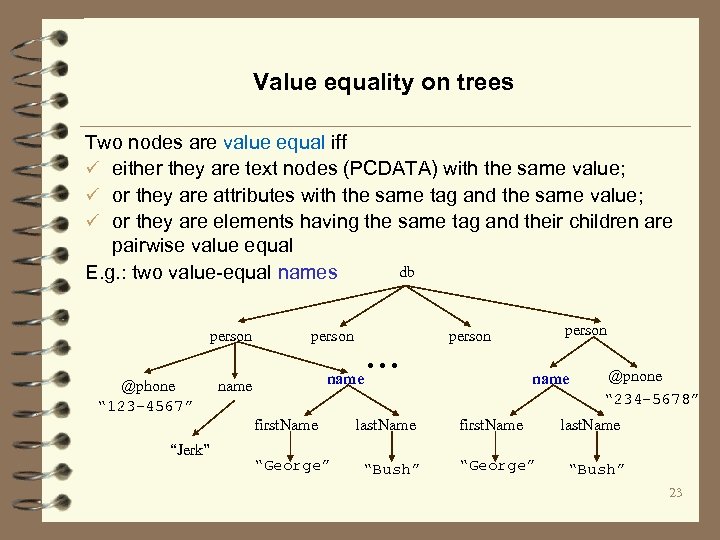
Value equality on trees Two nodes are value equal iff ü either they are text nodes (PCDATA) with the same value; ü or they are attributes with the same tag and the same value; ü or they are elements having the same tag and their children are pairwise value equal db E. g. : two value-equal names person @phone “ 123 -4567” person name first. Name “Jerk” “George” . . . last. Name “Bush” person name first. Name “George” @pnone “ 234 -5678” last. Name “Bush” 23

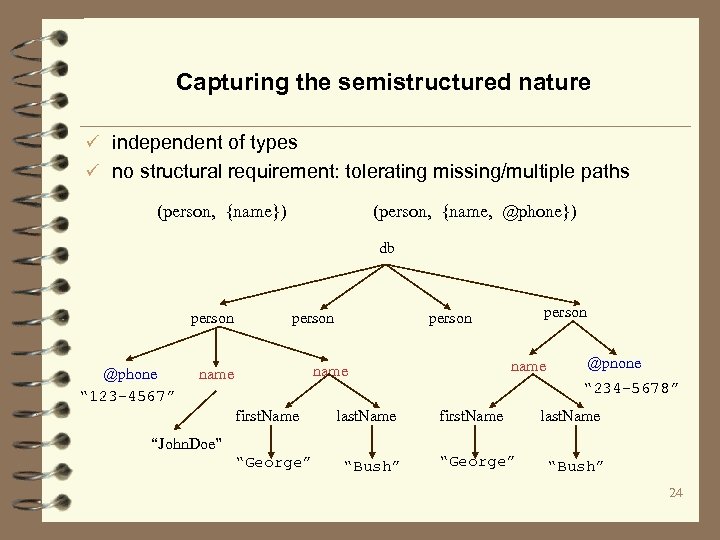
Capturing the semistructured nature ü independent of types ü no structural requirement: tolerating missing/multiple paths (person, {name}) (person, {name, @phone}) db person @phone “ 123 -4567” person name person @pnone “ 234 -5678” first. Name last. Name “John. Doe” “George” “Bush” 24

Relative path constraints [WWW’ 01] Relative key: (Q, K) ü path Q identifies a set [[Q]] of nodes, called the context path; ü K = (Q’, {P 1, . . . , Pk} ) is a key on sub-documents rooted at nodes in [[Q]] (relative to Q). Example. (//country, (province, {@capital})) (//country, {@name}) -- absolute key ü Absolute keys are a special case of relative keys: (Q, K) when Q is the empty path ü Similarly foreign keys Specification of XML constraints is more involved than its relational counterparts 25

Keys and foreign keys in XML Schema key: (Q, {P 1, . . . , Pk} ) ü Path expressions Q, Pi: fragments of XPath ü Uniqueness and existence: for each node x in [[Q]] and each i in [1, n], there exists a unique node yi reached via Pi, and yi is either a text node or an attribute Foreign keys: (Q, ü (S, {P 1, . . . , Pk} ) (S, {S 1, . . . , Sk} ) is a key ü Uniqueness and existence: both Pi and Si The uniqueness and existence condition complicates the consistency and implication analyses Absolute constraint 26

Other constraints for XML Functional dependencies: {P 1, . . . , Pk} {S 1, . . . , Sk} ü Generalizations of relational FDs – for deriving an extension of relational-schema normal forms ü Absolute constraints [Arenas and Libkin, PODS’ 02] XICs: x 1 … xn ( B(x 1, …, Xn) ∨ (i [1, l]) ( y 1 … yk Ci (x 1, …, xn, y 1, …, yk)) ü Generalization of relational embedded constraints ü B, Ci: conjunction of simple XPath expressions ü Subsuming relative keys and foreign keys (Deutsch and Tannen, [KRDB’ 01]) 27

Constraint analysis ü Analysis of XML constraints – Consistency analysis – Implication analysis – Absolute, relative, path-expression constraints 28

Consistency of XML specifications Given D: a DTD : a set of integrity constraints over D Consistency: Is there an XML document that both conforms to D and satisfies ? One wants to know whether XML specifications make sense! Run-time check: attempts to validate documents with (D, ). This would not tell us whether repeated failures are due to a bad specification or problems with the documents static analysis is desirable 29

An inconsistent specification The specification with D and is inconsistent! ü DTD D: <!ELEMENT db (province+, capital+)> <!ELEMENT province (city*, capital)> province. @name, capital. @in. Province ü Constraints : province. @name province capital. @in. Province province. @name In contrast, one can specify keys and foreign keys in SQL without worrying about their consistency with schema. 30

Cardinality constraints imposed by DTDs DTD D: <!ELEMENT db (province+, capital+)> <!ELEMENT province (city*, capital)> Variables: ü Xprovince: the number of province elements under the root ü Xcapital: the number of capital subelements of the root ü Ycapital: the number of capital subelements of province’s Xprovince 1, Xcapital 1 |ext(province)| = Xprovince, Xprovince = Ycapital |ext(capital)| = Xcapital + Ycapital |ext(capital)| > |ext(province)| 32

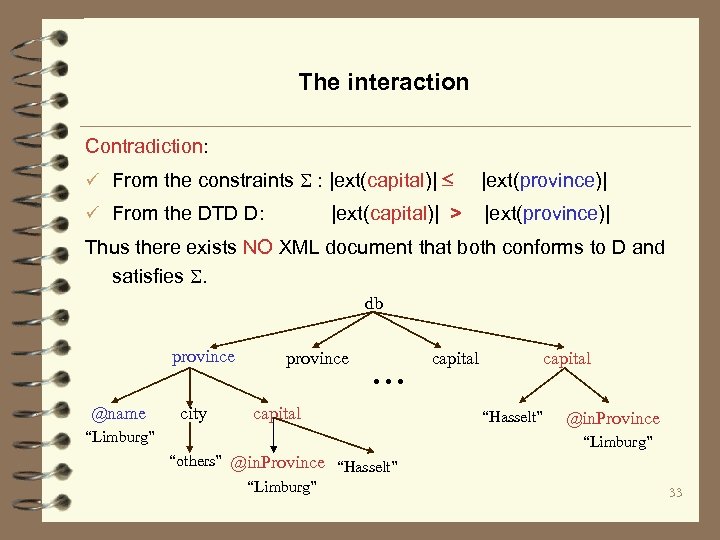
The interaction Contradiction: ü From the constraints : |ext(capital)| |ext(province)| ü From the DTD D: |ext(province)| |ext(capital)| > Thus there exists NO XML document that both conforms to D and satisfies . db province @name city province . . . capital “Limburg” capital “Hasselt” @in. Province “Limburg” “others” @in. Province “Hasselt” “Limburg” 33

Consistency analysis [PODS’ 01, 02, JACM, SICOMP] ü Trivial for relational databases: given any schema and keys, foreign keys, one can always find a nonempty instance of the schema satisfying the constraints. ü Hard for XML: XML specifications may not be consistent! – Both DTDs and constraints impose cardinality constraints – The interaction between these two classes of cardinality constraints is rather complicated. 34

Consistency analysis of XML constraints Theorem: The consistency problem is ü undecidable for multi-attribute absolute keys and foreign keys; ü NP-complete for unary absolute keys and foreign keys, even for primary keys (primary: at most one key for each element type); ü in NEXPTIME for primary multi-attribute absolute keys and unary foreign keys ü in 2 NEXPTIME and PSPACE-hard for unary absolute regular keys and foreign keys (target path: / , where is a regular path expression and an element type; key paths: attributes) ü undecidable for relative keys and foreign keys, even when all the constraints are unary and primary. As opposed to the trivial analysis of the relational counterpart. 35

Proof ideas ü Multi-attribute constraints: reduction from the implication problem for functional and inclusion dependencies in RDBs. ü Unary keys and foreign keys: – a nontrivial encoding of DTDs and unary constraints in terms of linear integer constraints (O(n 2 log n)-time); – polynomially equivalent to LIP, linear integer programming ü Multi-attribute primary keys and unary foreign keys: – polynomially equivalent to Prequadratic Diophantine Problem (PDE): satisfiability of linear integer constraints and prequadratic constraints of the form: x <= y z; – the precise complexity of PDE, a restriction to the Hilbert’s 10 th problem, is open -- nontrivial. 36

Proof idea for relative constraints Theorem: The consistency problem is undecidable for relative keys and foreign keys, even when all the constraints are unary and are under the primary key restriction. As opposed to the NP complexity of its absolute counterpart. Proof idea: reduction from the Hilbert’s 10 th problem. Diophantine equation problem: P 1 (x 1, …, xk) = Q 1 (x 1, …, xk) + c 1. . . Pn (x 1, …, xk) = Qn (x 1, …, xk) + cn 37

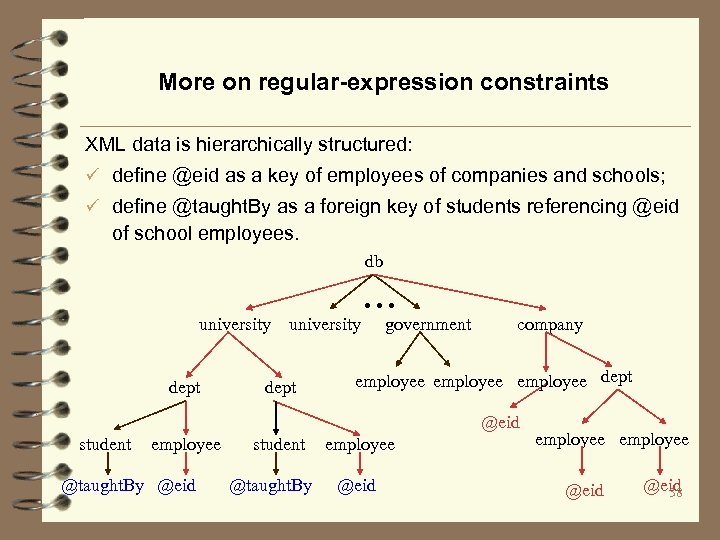
More on regular-expression constraints XML data is hierarchically structured: ü define @eid as a key of employees of companies and schools; ü define @taught. By as a foreign key of students referencing @eid of school employees. db university dept . . . government company employee dept @eid student employee @taught. By @eid student @taught. By employee @eid 38

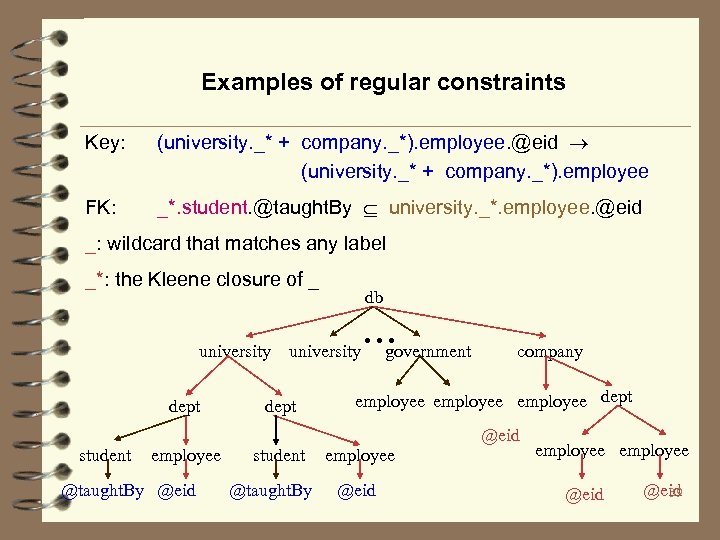
Examples of regular constraints Key: (university. _* + company. _*). employee. @eid (university. _* + company. _*). employee FK: _*. student. @taught. By university. _*. employee. @eid _: wildcard that matches any label _*: the Kleene closure of _ university dept student employee @taught. By @eid db university dept student @taught. By . . . government company employee dept employee @eid 39

Regular path expression Vertical regular expressions: : : = | | _ | . | + | * : empty word; : element type; _: wildcard; “. , +, *”: concatenation, disjunction, Kleene star Example: (university. _* + company. _*). employee university. _*. employee nodes(. ): the set of elements in an XML document that are reachable from the root by following 40

Regular expression constraints ü key: . [X] . . A document satisfies the key iff x y nodes( . ) ( l X (x. l = y. l) x = y) ü foreign key: 1. 1[X] 2. 2[Y], and a key 2. 2[Y] 2. 2 A document satisfies the FK iff it satisfies the key and x nodes( 1. 1 ) y nodes( 2. 2 ) (x[X] = y[Y]) where nodes(. ): the set of elements reachable from the root by following . 41

Regular: an extension of absolute constraints Example: Key: (university. _* + company. _*). employee. @eid (university. _* + company. _*). employee _*. student. @taught. By university. _*. employee. @eid FK: Observation: nodes( _*. ) = ext( ) Recall absolute constraints: ü key: [X] _*. [X] _*. ü foreign key: 1[X] 2[Y], 2[Y] 2 _*. 1 [X] _*. 2 [Y], _*. 2 [Y] _*. 2 42

Consistency analysis of regular constraints Corollary: The consistency problem is undecidable for multiattribute regular keys and foreign keys. Theorem: It is decidable in 2 NEXPTIME and is PSPACE-hard for unary regular constraints. 2 NEXPTIME: an involved encoding in terms of LIP ü regular expressions in a DTD interact with (vertical) regular path expressions: reduce DTD to a simple normal form ü regular path expressions interact with each other: introduce exponentially many variables for all boolean combinations ü encoding “reachability” (nodes(. )) of a path expression: tag variables with states of finite state automata 43

Some tractable cases ü Restrictions on constraints. Theorem: For multi-attribute relative keys only, the consistency problem is in linear time for arbitrary DTDs. Recall relative keys: country (province. @name province) In contrast, due to the existence and uniqueness condition: Theorem: It is intractable for unary keys alone in XML Schema. ü Restrictions on DTDs: Theorem: When DTD is fixed, the consistency problem is in PTIME for absolute unary keys and foreign keys. In practice, DTD is designed at one time, but constraints are written in stages: constraints are incrementally added. 44

Implication analysis [PODS’ 00, 01, 02, DBPL’ 01] Given D: a DTD : a set of constraints expressed in C : a property (a constraint of C) Implication (C ): Is it the case that for any XML document, if it conforms to D and satisfies , then it must satisfy ? C: a constraint language The need for studying implication: ü data integration: constraints checking at virtual views ü optimization of XML queries and XML relational storage ü design theory for XML specifications: normalization 45

Some complexity results for implication analysis Theorem: The implication problem is ü undecidable for multi-attribute absolute keys and foreign keys, and for unary relative keys and foreign keys; ü PSPACE-hard for unary regular absolute keys and foreign keys; ü co. NP-complete for unary absolute keys and foreign keys. ü co. NP-hard for XML-Schema unary keys ü in linear time for absolute multi-attribute keys; ü in PTIME for arbitrary absolute keys and foreign keys when the DTD is fixed, and ü in PTIME for relative path keys in the absence of DTDs The analysis of XML constraints is far more intricate than its relational counterpart 46

Applications ü Application of XML constraints, and open problems – Constraint propagation – Schema-directed XML integration – Normal form – Query rewriting/optimization – Update processing – Data cleaning –. . . 47

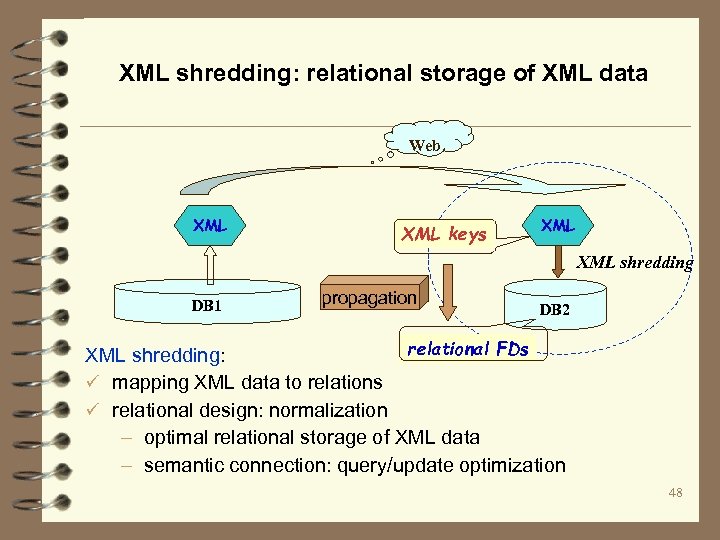
XML shredding: relational storage of XML data Web XML keys XML shredding DB 1 propagation DB 2 relational FDs XML shredding: ü mapping XML data to relations ü relational design: normalization – optimal relational storage of XML data – semantic connection: query/update optimization 48

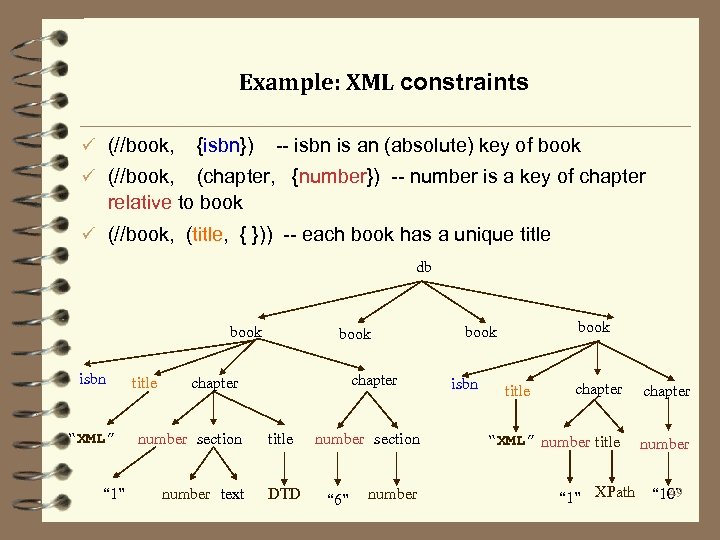
Example: XML constraints ü (//book, {isbn}) -- isbn is an (absolute) key of book ü (//book, (chapter, {number}) -- number is a key of chapter relative to book ü (//book, (title, { })) -- each book has a unique title db book isbn “XML” “ 1” title book chapter number section number text title DTD number section “ 6” number book isbn chapter “XML” number title “ 1” XPath 49 “ 10”

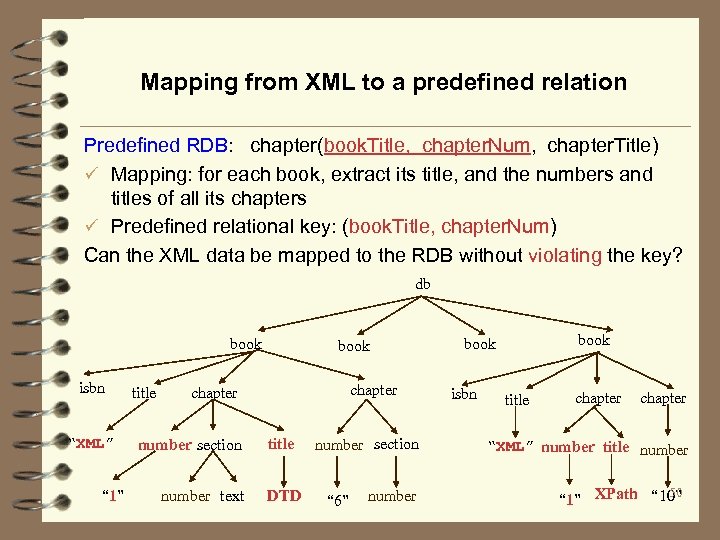
Mapping from XML to a predefined relation Predefined RDB: chapter(book. Title, chapter. Num, chapter. Title) ü Mapping: for each book, extract its title, and the numbers and titles of all its chapters ü Predefined relational key: (book. Title, chapter. Num) Can the XML data be mapped to the RDB without violating the key? db book isbn “XML” “ 1” title book chapter number section number text title DTD number section “ 6” number book isbn title chapter “XML” number title number 50 “ 1” XPath “ 10”

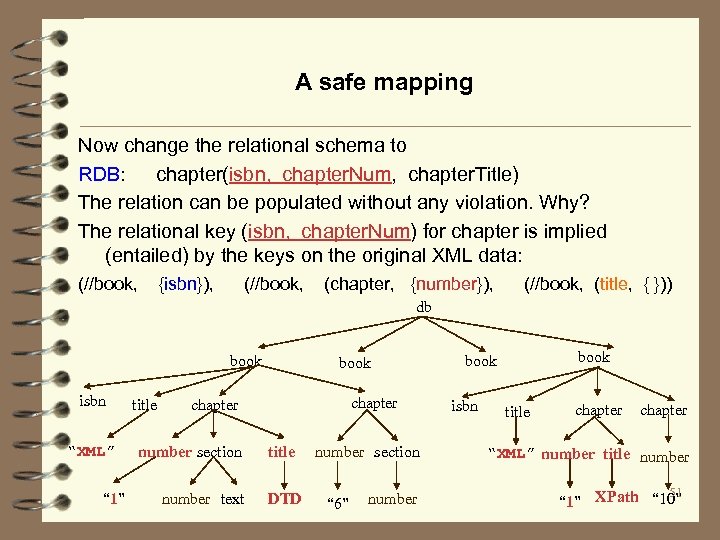
A safe mapping Now change the relational schema to RDB: chapter(isbn, chapter. Num, chapter. Title) The relation can be populated without any violation. Why? The relational key (isbn, chapter. Num) for chapter is implied (entailed) by the keys on the original XML data: (//book, {isbn}), (//book, (chapter, {number}), (//book, (title, { })) db book isbn “XML” “ 1” title book chapter number section number text title DTD number section “ 6” number book isbn title chapter “XML” number title number 51 “ 1” XPath “ 10”

Constraint Propagation [ICDE’ 03, JCSS] ü Input: – a set K of XML keys (context and target path: a fragment of XPath, key paths: attributes) – a predefined relational schema S, – a mapping f from XML to S (XPath, projection, join, union) – and a relational functional dependency FD over S ü Output: is the FD propagated from K via f? I. e. , does FD hold over the DB f(T) for any XML document T that satisfies K? Theorem: The constraint propagation problem is in PTIME. ü Checking the consistency of a predefined relational schema for storing XML data ü XML schema/DTD is not required – K is the only semantics 52

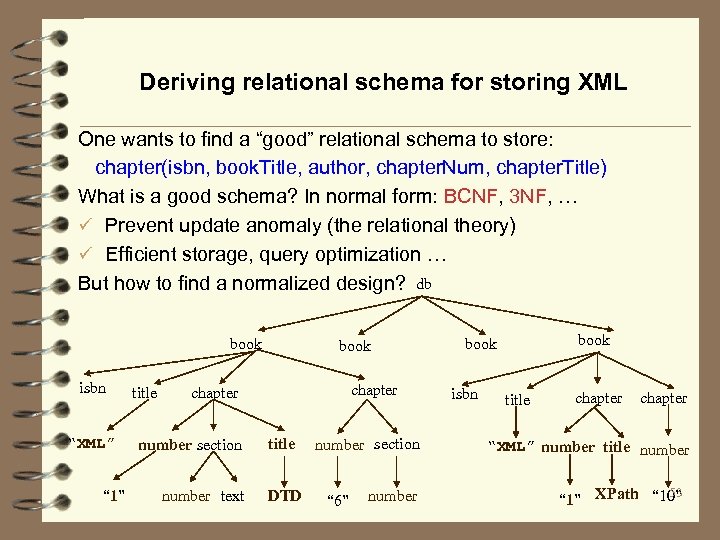
Deriving relational schema for storing XML One wants to find a “good” relational schema to store: chapter(isbn, book. Title, author, chapter. Num, chapter. Title) What is a good schema? In normal form: BCNF, 3 NF, … ü Prevent update anomaly (the relational theory) ü Efficient storage, query optimization … But how to find a normalized design? db book isbn “XML” “ 1” title book chapter number section number text title DTD number section “ 6” number book isbn title chapter “XML” number title number 53 “ 1” XPath “ 10”

Constraint propagation and normalization From the given XML keys: (//book, {isbn}), (//book, (chapter, {number}), (//book, (title, { })) one can derive functional dependencies: isbn book. Title, isbn, chapter. Num chapter. Title Normalize the relation by using these functional dependencies: chapter(isbn, book. Title, author, chapter. Num, chapter. Title) book(isbn, book. Title), chapter(isbn, chapter. Num, chapter. Title), author(isbn, author) The new schema is in BCNF! 54

Computing minimum cover of propagated FDs ü Input: a set K of XML keys, and a mapping f from XML to a universal schema U ü Output: a minimum cover F of all the functional dependencies (FDs) propagated from the XML keys K via f – F is a cover (a set of FDs): any FD propagated from K via f is implied by F – F is minimum: F contains no redundant FDs, i. e. , any FD in F is not entailed by other FDs in F. Theorem: There is a PTIME algorithm for computing a minimum cover of propagated FDs. Normalize relational schema for storing/querying XML data! 55

Research issues For general constraints/mapping languages: undecidable ü if the mapping language is relationally complete (selection, projection, join, union, difference), even for XML keys alone ü if both XML keys and foreign keys are considered, even for the identity “transformation” Open: ü To identify (a) practical mapping languages and (b) practical XML constraints that allow efficient constraint propagation ü Constraint propagation from relations to XML – Information preserving (lossless) data exchange – Query/update rewriting/optimization – Overcoming incompleteness of source data (foreign keys) 56

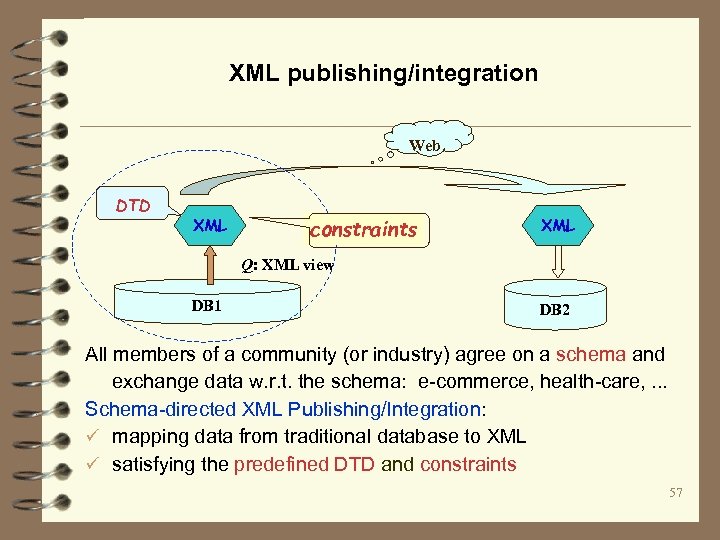
XML publishing/integration Web DTD XML constraints XML Q: XML view DB 1 DB 2 All members of a community (or industry) agree on a schema and exchange data w. r. t. the schema: e-commerce, health-care, . . . Schema-directed XML Publishing/Integration: ü mapping data from traditional database to XML ü satisfying the predefined DTD and constraints 57

Schema-directed integration [SIGMOD’ 03] DTD DB integration DB DB multiple, distributed sources constraints XML view üSchema-directed: XML view conforming to a schema (D, ) – D: a DTD – : a set of XML constraints (relative keys, foreign keys) ü Attribute Integration Grammar (AIG) DTD-directed view definition: recursive, nondeterministic Inherited and synthesized attributes Constraint compilation: automatically captures integrity constraints and DTD in a uniform framework 58

XML normal forms ü 3 NF, BCNF? ü Extensions of (nested) relational normal forms, via XML FDs – M. Arenas and L. Libkin. A Normal Form for XML Documents, [PODS 02]. XNFs, decomposition algorithms, complexity, … – M. Vincent, J. Liu and C. Liu. Strong functional dependencies and their application to normal forms in XML. [TODS 29(3), 2004] – X. Wu, T. W. Ling, S. Lee, M. Lee, G. Dobbie. NF-SS: A Normal Form for Semistructured Schema. [ER (Workshops) 2001] 59

Research issues for XML normal forms ü Implication analysis: more intriguing than relational FDs ü Relative functional dependencies: hierarchical nature of XML ü “Right” normal form for XML: to prevent update anomalies? – XML data is often “static”: update anomalies? – XML data is typically stored in RDBMS – When XML data is updated, it is done through RDBMS – Redundancy often helps, e. g. , performance and reliability – Normal form: a right class of constraints to assure “lossless” shredding into relations of certain normal form Unfortunately, no previous work has studied this 60

Run-time analysis: incremental constraint checking Input: XML tree T, constraints , update ∆T, where T satisfies Question: does (T + ∆T) satisfy ? ü ∆X. Code generator: incremental checking. Lucent applications M. Benedikt, G. Brun, J. Gibson, R. Kuss and A. Ng. Automated update management for XML integrity constraints. [PLANX’ 02] ü Application of incremental techniques for attribute grammar M. Abrao, B. Bouchou, M. Alves, D. Laurent, M. Musicante. Incremental Constraint Checking for XML Documents [XSym’ 04] Research issues: ü Complexity of incremental constraint checking ü XML editors: broken link detection and repair ü Incremental checking techniques for XML data stored in RDBMS 61

Query rewriting and optimization Query translation from XQuery to SQL: XML data stored in RDBMS – encode XIGs and XQuery in relational queries and constraints – extensions of chase and backchase A. Deustch and V. Tannen – Reformulation of XML Queries and Constraints [ICDT’ 03] – MARS: A System for Publishing XML from Mixed and Redundant Storage [VLDB’ 03] R. Krishnamurthy, R. Kaushik, J. Naughton. Efficient XML-to-SQL Query Translation: Where to Add the Intelligence? [VLDB 2004] Research issues: ü Rewriting queries over (recursive security) views of XML data ü Query optimization for (compressed) XML data in native store 62

Data cleaning Input: XML tree T, constraints , DTD D Question: if T does not satisfy D + , find a repair T’ such that (a) T’ satisfies D + , and (b) the distance between T and T’ is minimal (update operations: insert, delete, modify) ü G. Flesca, F. Furfaro, S. Greco, E. Zumpano. Repairs and Consistent Answers for XML Data with Functional Dependencies [XSym’ 03] Research issues: ü Effective techniques for repairing integrated XML data: conflicts and inconsistencies may emerge as violations of constraints. – Various constraint languages, – XML schema ü Automated tools for repairing Web pages: broken links 63

Summary ü Specification of XML constraints: – absolute vs. relative, path constraints: XML data is hierarchical and semi-structured – mild extensions of relational constraints are not sufficient ü Consistency and implication analysis of XML constraints – DTDs interact with XML constraints – far more intricate than their relational counterparts ü Applications of XML constraints – XML storage, query, update, integration, cleaning, … – many practical issues remain to be explored 64

References In addition to the papers mentioned earlier ü Keys for XML Computer Networks, Volume 39(5), August 2002, pp 473 - 487. P. Buneman, S. Davidson, W. Fan, C. Hara, W. Tan ü On XML Integrity Constraints in the Presence of DTDs Journal of the ACM (JACM), 49(3), pp 368 - 406, May 2002. Wenfei Fan and Leonid Libkin ü On Verifying Consistency of XML Specifications PODS 2002 Marcelo Arenas, Wenfei Fan and Leonid Libkin ü What's Hard about XML Schema Constraints? DEXA 2002 Marcelo Arenas, Wenfei Fan and Leonid Libkin 65

References ü Propagating XML Constraints to Relations JCSS, 73(3): 316 -361, May 2007. Susan Davidson, Wenfei Fan, and Carmem Hara ü Capturing both Types and Constraints in Data Integration SIGMOD, 2003 M. Benedikt, C. Chan, W. Fan, J. Freire, and R. Rastogi ü XML Constraints: Specification, Analysis, and Applications LAAIC, 2005 Wenfei Fan ü Containment and Integrity Constraints for XPath KRDB 2001 Alin Deutsch, Val Tannen 66