Химия — теоретические основы Анатолий Анатольевич БАРУНИН

Химия - теоретические основы Анатолий Анатольевич БАРУНИН - лектор Литература: 1, 2. А. П. КИСЕЛЕВ, А. А. КРАШЕНИННИКОВ. Основы общей химии: 1 -Уч. пос. 2012 г. одной книгой(1262) 2 -Уч. пос. (ч. 1, 2, 3)2002 -2007 г. 2 – Уч. пос. Часть 1 Строение вещества 2002 г. (552) Часть 2 Термодин. и кинетика химического процесса 2003(599) г. (599) 3 Электрохим. и коррозионные процессы 2007(837) Часть 3. Учебные пособия и метод. указания кафедры 4. А. И. Горбунов, А. А. Гуров и др. Теоретические основы общей химии 5. А. В. Суворов, А. Б. Никольский 6. В. В. Фролов 7. Н. В. Коровин - учебники для вузов

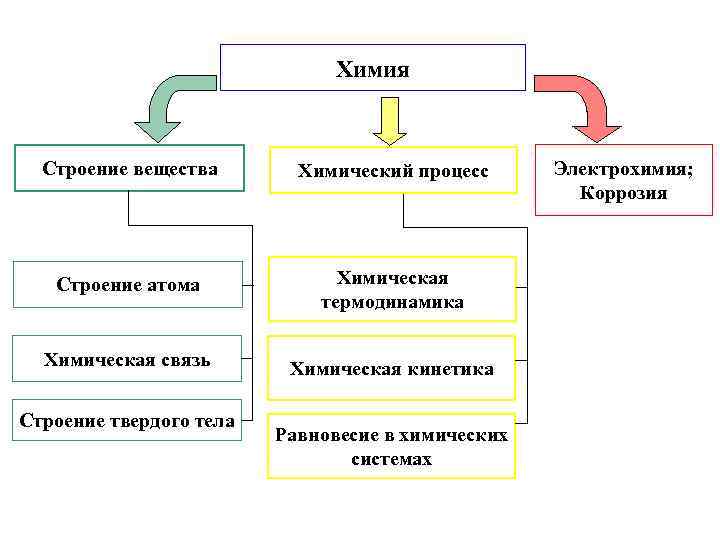
Химия Строение вещества Химический процесс Строение атома Химическая термодинамика Химическая связь Химическая кинетика Строение твердого тела Равновесие в химических системах Электрохимия; Коррозия

I. Строение атома 3 этапа развития учения о строении атома 1 – Натурфилософские представления об атомном строении материи. (5 в. до н. э. ) Демокрит – понятие «атом» . Эпикур, Аристотель 2 – Химическая гипотеза об атоме, как наименьшей частице химического элемента. Атомы отличаются массой. Парацельс, Бойль, Берцелиус (16 -17 в. ) 3 – Физические модели. Описывают сложное строение атома (на рубеже 1920 в. по настоящее время) на основании: Исследование электролиза(1832) Майкл Фарадей Открытие каналовых (1886) и катодных лучей (1896) Уильям Крукс Открытие и измерение свойств электрона (1897) Джозеф Джон Томсон Открытие естественной радиоактивности (1896) Анри Беккерель Атомы содержат разноименно заряженные частицы

Строение атома. Физические модели строения атома Эрнест Резерфорд - Планетарная модель атома (1911 г. ) Атом - сложная частица, состоящая из положительно заряженного ядра (~10 -15 м) и отрицательно заряженных электронов вращающихся вокруг ядра на расстоянии ~10 -10 м (по характеру рассеяния α-частиц тонкими Pt, Ag и Cu металлическими фольгами) Нильс Бор – теория (модель) строения атома водорода (постулаты) (1913 г. ) En = - 2π2 e 4 k 2 m / h 2 ∙ 1/n 2 (n=1 E 1= -13, 6 э. В; En = - E 1 / n 2 rn = h 2 / 4π2 e 2 km ∙ n 2 n = 1, 2, 3…. . Эрвин Шредингер - [квантово-механическая модель] Квантовая (волновая) механика - теория, устанавливающая способ описания и законы движения микрочастиц (1926 г. )

Корпускулярно-волновой дуализм свойств материи [проблема природы лучистой энергии - эл. магн. излучения(ЭМИ)] Частица: m - масса p = mv - импульс E= mv 2/2 - кинетическая энергия Волна: - длина волны n- частота Т - период Электромагнитное излучение Макс Планк E = h n – энергия кванта ЭМИ 1900 г. тела (дискретная порция) h = 6, 6262 10 -34 Дж с - постоянная Планка n- частота излучения [с– 1] нагретого квант энергии любого ЭМИ– частица фотон Альберт Эйнштейн E = 1905 г. m - масса фотона, кг c = 2, 9979 108 м/сек - скорость света m c 2 hn = mc 2 Корпускулярноволновой дуализм ЭМИ: фотон - частица и/или волна p = m c - импульс фотона

Луи де Бройль (дуализм-общее свойство материи, Частица: m - масса, v – скорость а не только ЭМИ) - гипотезапостулат о связи импульса P любого движущегося матер. объекта с длиной волны λ, представляющей волновой хар-р его движения (1924) г. Кинетическая энергия электрон Длина волны - m = 9, 11 10 -31 кг Ek = 100 э. В (1 э. В=1, 602 10 -19 Дж) , = 1. 2 Å (1 Å =10 -10 м) Дифракционная решеткакристалл. плоскости Ме монокристаллов = 1. 2 Å (Ni фольга) α- постоянная решетки

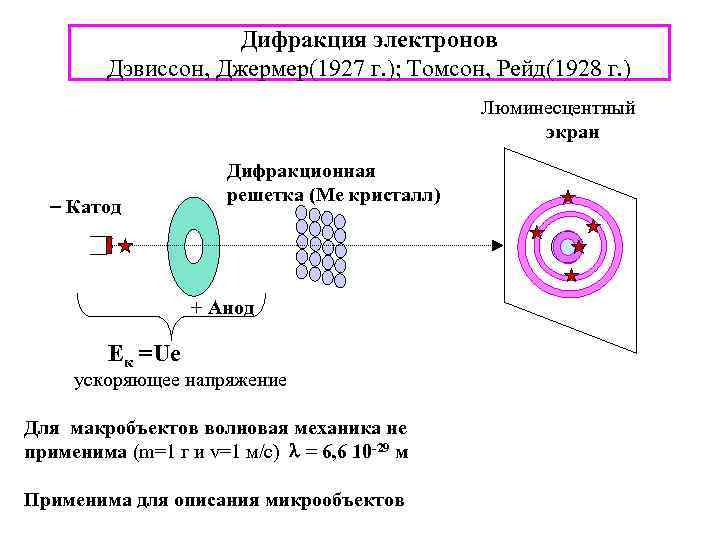
Дифракция электронов Дэвиссон, Джермер(1927 г. ); Томсон, Рейд(1928 г. ) Люминесцентный экран Катод Дифракционная решетка (Ме кристалл) + Анод Ек =Uе ускоряющее напряжение Для макробъектов волновая механика не применима (m=1 г и v=1 м/с) = 6, 6 10 -29 м Применима для описания микрообъектов

Принцип неопределенности [для микрочастиц(электрона)] Вернер Гейзенберг постулировал этот принцип в 1927 г. Точное определение координат частицы и ее импульса невозможно и заменяется определением вероятности нахождения частицы в какой-то области пространства Р - вероятность 0 Р 1 Эрвин Шредингер – квантово-механическая модель строения атома на основе квантовой (волновой) механики - теории, устанавливающей способ описания и законы движения микрочастиц - базируется на 2 -х основных гипотезах-постулатах Л. Де Бройля и В. Гейзенберга

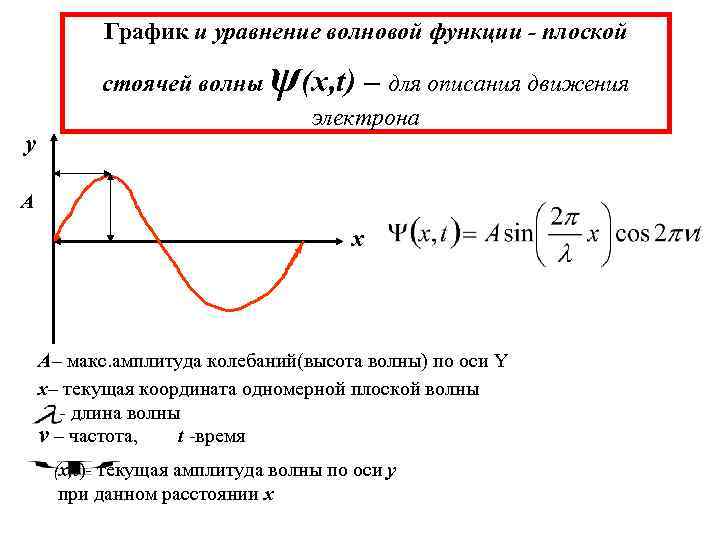
График и уравнение волновой функции - плоской стоячей волны y ψ(x, t) – для описания движения электрона A x А– макс. амплитуда колебаний(высота волны) по оси Y х– текущая координата одномерной плоской волны - длина волны ν – частота, t -время (x, t)- текущая амплитуда волны по оси y при данном расстоянии x

Уравнение Шредингера 1. Уравнение отображает волновой характер движения электрона в пространстве с координатами (x, y, z) (x, y, z, t) - волновая функция - пси функция (стоячая волна) - Текущая амплитуда, функция координат (x, y, z) и времени (t) (x, y, z) – (стоячая волна)стационарный процесс – Текущая амплитуда, функция координат (x, y, z); пусть cos 2πνt=1 Дифф. уравнение 2 -го порядка стоячей волны для стационарного процесса - длина волны 2 - оператор Лапласа(набла два)

2. Уравнение должно содержать в себе характеристики электрона как волны - , так и частицы - m (дуализм микромира) m, Ek Длина волны де Бройля Волновое уравнение движения свободного электрона: E = Ek + V E - полная энергия V- потенциальная энергия Эрвин Шрeдингер: Волновое уравнение микрочастицы(электрона) в потенциальном поле(в атоме) 1926 г.

Физический смысл волновой функции Макс Борн, 1926 г. (x, y, z) - пси функция - волновая функция • волновая функция(амплитудная) и физического смысла не имеет • 2(x, y, z) - квадрат волновой функции пропорционален вероятности (d. P) нахождения частицы в элементарном объеме (d. V) d. P = 2(x, y, z) d. V Вероятность Pv нахождения частицы в объеме V: Плотность вероятности (электронная плотность) вероятность нахождения в элементарном объеме d. V с коордиатами dx, dy, dz: Принцип нормирования волновых функций PV = ∫v A 2 |Ψ(x, y, z) |2 d. V = 1, А –нормирующий множитель

Электрон в одномерном потенциальном ящике(яме). Решение ур. Шредингера. Потенциальная яма (ящик) - область пространства, вне которой потенциальная энергия электрона обращается в бесконечность, т. е электрон не может выйти за границы ящика (связанное состояние)V 0 модель для электрона в атоме a • Одномерный потенциальный ящик Граничные условия: внутри ящика: V=0 (x) на границах ящика: V= (0)=0; (а)=0 Решение – нахождение собственных функций(конечны, однозначны, непрерывны) и расчет соответствующих этим функциям значений собственных энергий x

• Нахождение волновой функции состояния электрона в потенц. ящике Общее решение ур. Шредингера Граничные условия A 0 n=1, 2, 3…. . Из условия нормировки Решение в явном виде - набор волн. функций Ψ(х), где a параметр потенциального ящика, n = 1, 2, 3…- квантовое число

• Нахождение энергии электрона Набору ᴪ(x) соответствует набор Е, n = 1, 2, 3…- квантовое

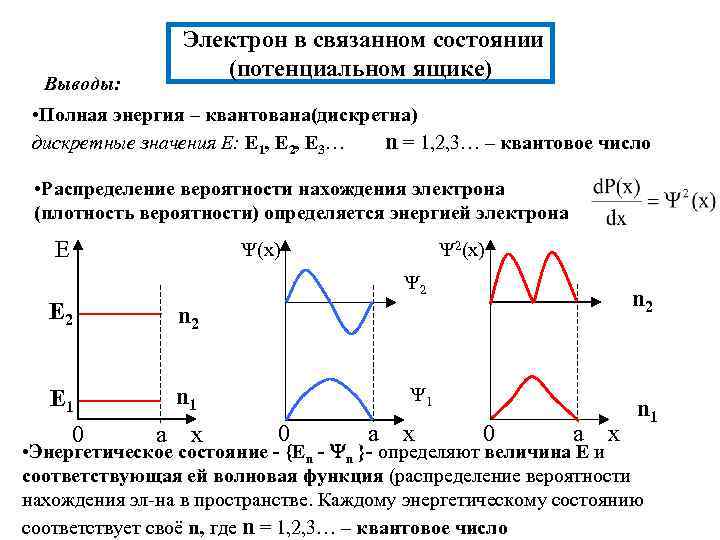
Электрон в связанном состоянии (потенциальном ящике) Выводы: • Полная энергия – квантована(дискретна) дискретные значения Е: E 1, E 2, E 3… n = 1, 2, 3… – квантовое число • Распределение вероятности нахождения электрона (плотность вероятности) определяется энергией электрона E 2(x) 2 E 2 n 2 E 1 0 n 1 n 2 а x 1 0 а x n 1 • Энергетическое состояние - {En - n }- определяют величина Е и соответствующая ей волновая функция (распределение вероятности нахождения эл-на в пространстве. Каждому энергетическому состоянию соответствует своё n, где n = 1, 2, 3… – квантовое число

Электрон в трехмерном потенциальном ящике Решение: • Набор волновых функций: a, b, c – параметры ящика nx, ny, nz – квантовые числа • Набор энергий: Выводы: 1. Энергия электрона квантована. 2. Энергетическое состояние определяется набором целочисленных параметров - трех квантовых чисел nx. ny, nz.

Вырожденные энергетические состояния одно значение энергии – несколько наборов квантовых чисел несколько волновых функций а=b=c Е, Е 5 = 12 Е 4 = 11 [2, 2, 2] [3, 1, 1] [1, 3, 1] [1, 1, 3] Е 3 = 9 [2, 2, 1] [1, 2, 2] [2, 1, 2] Е 2 = 6 [2, 1, 1] [1, 2, 1] [1, 1, 2] Е 1 = 3 [1, 1, 1] Трехкратная степень вырождения

Квантово-механическая модель атома. Основное состояние атома водорода [k=1/4πε 0] - константа в з-не Кулона -ē r +ē Основное состояние Еmin z r x y x = r sin cos y = r sin z = r cos Ψ(r) – волновая функция (собственная функция), явл. решением ур. Шредингера, а – const, А – нормирующий коэффициент

Решение уравнения Шредингера для основного состояния атома водорода подставляем в уравнение Шредингера

Решение системы Из принципа нормировки: Сходимость значений Е расчетной и экспериментальной (-13, 6 э. В) – модель имеет право на существование

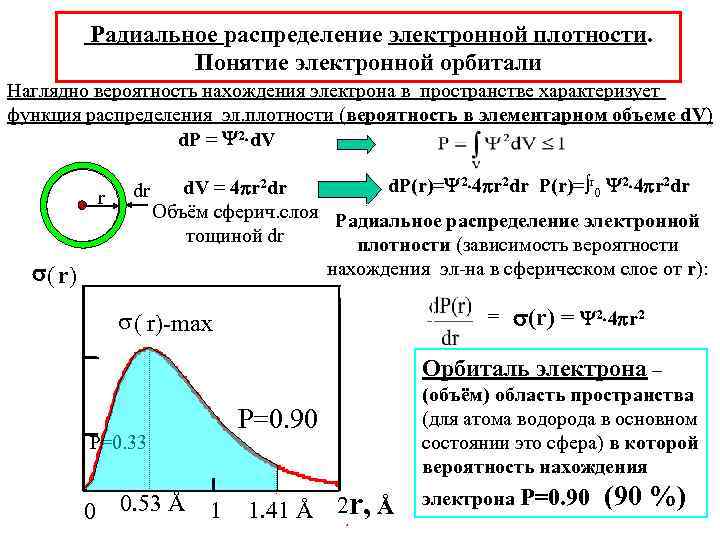
Радиальное распределение электронной плотности. Понятие электронной орбитали Наглядно вероятность нахождения электрона в пространстве характеризует функция распределения эл. плотности (вероятность в элементарном объеме d. V) d. P = 2 d. V r dr ( r) d. P(r)= 2 4 r 2 dr P(r)=∫r 0 2 4 r 2 dr d. V = 4 r 2 dr Объём сферич. слоя Радиальное распределение электронной тощиной dr плотности (зависимость вероятности нахождения эл-на в сферическом слое от r): s ( r)-max = (r) = 2 4 r 2 Орбиталь электрона – P=0. 90 P=0. 33 0 0. 53 Å 1 1. 41 Å 2 r, Å (объём) область пространства (для атома водорода в основном состоянии это сфера) в которой вероятность нахождения электрона P=0. 90 (90 %)

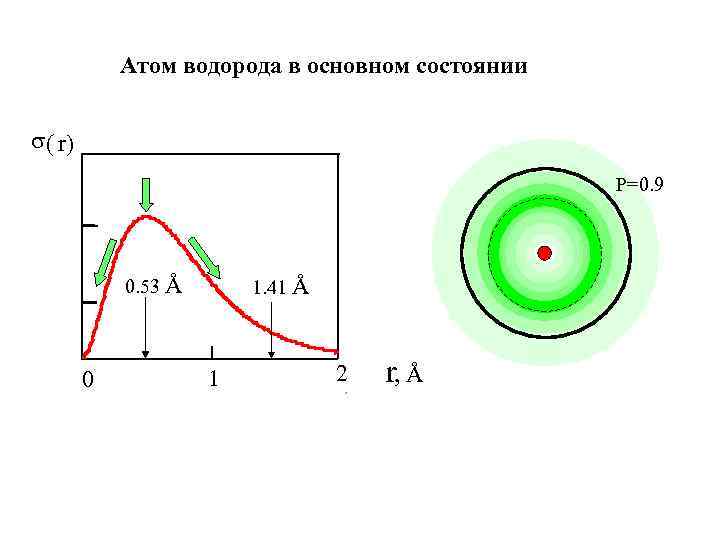
Атом водорода в основном состоянии s( r) Р=0. 9 0. 53 Å 0 1. 41 Å 1 2 r, Å

Возбужденные состояния атома водорода Общий вид волновой функции - (r, , ). Используя метод разделения переменных (r, , ) представляют в виде R(r) Y( , ) R(r)n, l -функция радиального распределения электронной плотности в явном виде(получают при решении ур. Шреденгера) содержит n и l Y( , )l, m -функция углового распределения электронной плотности в явном виде(получают при решении ур. Шреденгера) содержит l и m n, l, m - целочисленные параметры волновых функций в явном виде – наз. квантовыми числами Определяют набор собственных волн. функций(решений ур. Шредингера) и соответствующий им набор энергетических состояний{En- n, l, m } в атоме водорода Квантовые числа: главное – n = 1, 2, 3, 4… орбитальное – l = 0, 1, 2, 3. . . (n -1) магнитное – m = -l, (-l+1), . . . , 0, . . . , (+l– 1), +l спиновое – ms =± 1/2 (1933 г. ) Поль Дирак, модель Уленбека и Гаудсмита

Квантовые числа главное : n = 1, 2, 3, 4… Определяет разрешенные (квантованные, дискретные) значения полной энергии электрона, размер орбитали(расстояния е до ядра) орбитальное : l = 0, 1, 2, 3. . . (n-1) Возможные квантовые значения орбитального момента кол. движения электрона(Екин -форма орбитали) l=2 l=0 l=1 s- орбиталь р- орбиталь магнитное : m = -l, (-l+1), . . . , 0, . . . , (l-1), +l Разрешенные направления в пространстве вектора орбит. момента кол. движения-число орбиталей(Епот –зависит от положения е в пространстве) р- орбиталь m = 1, 0, -1 s- орбиталь- m = 0 cпиновое : ms ± 1/2 Собственный момент кол. движения d- орбиталь pz px py

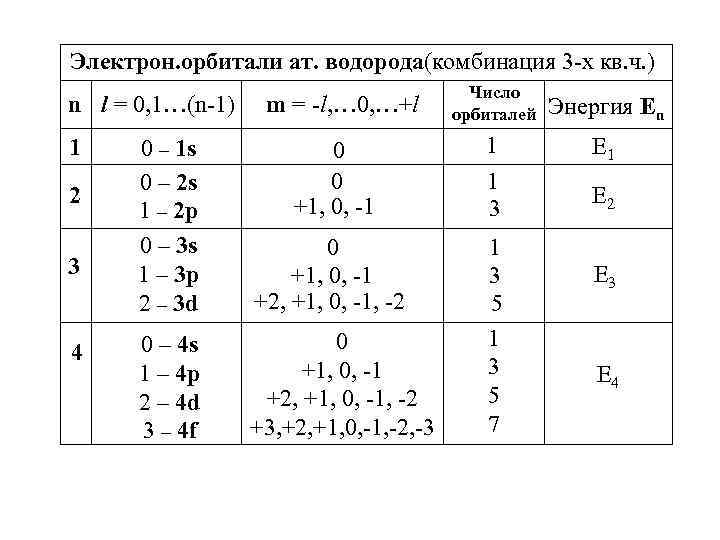
Электрон. орбитали ат. водорода(комбинация 3 -х кв. ч. ) n l = 0, 1…(n-1) 1 2 3 4 m = -l, … 0, …+l Число орбиталей Энергия Еn 0 – 1 s 0 – 2 s 1 – 2 p 0 – 3 s 1 – 3 p 2 – 3 d 0 0 +1, 0, -1 1 E 1 1 3 E 2 0 +1, 0, -1 +2, +1, 0, -1, -2 0 – 4 s 1 – 4 p 2 – 4 d 3 – 4 f 0 +1, 0, -1 +2, +1, 0, -1, -2 +3, +2, +1, 0, -1, -2, -3 1 3 5 7 E 3 E 4

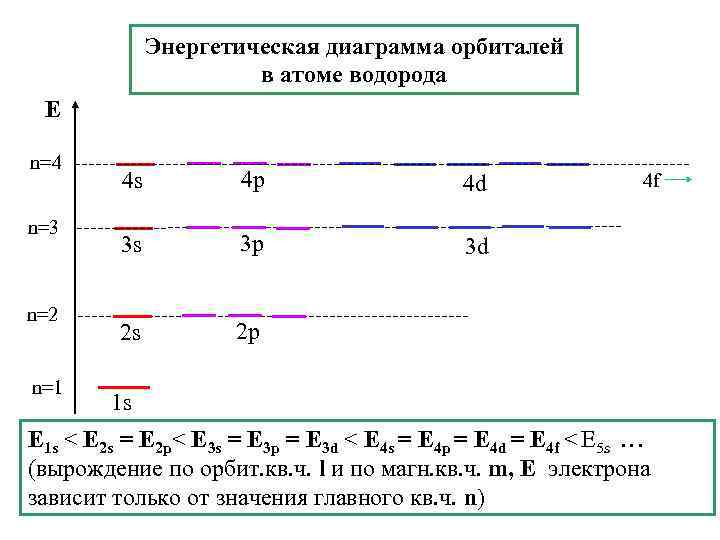
Энергетическая диаграмма орбиталей в атоме водорода Е n=4 n=3 n=2 n=1 4 s 4 p 4 d 3 s 3 p 3 d 2 s 2 p 4 f 1 s E 1 s < E 2 s = E 2 p< E 3 s = E 3 p = E 3 d < E 4 s = E 4 p = E 4 d = E 4 f < E 5 s … (вырождение по орбит. кв. ч. l и по магн. кв. ч. m, Е электрона зависит только от значения главного кв. ч. n)

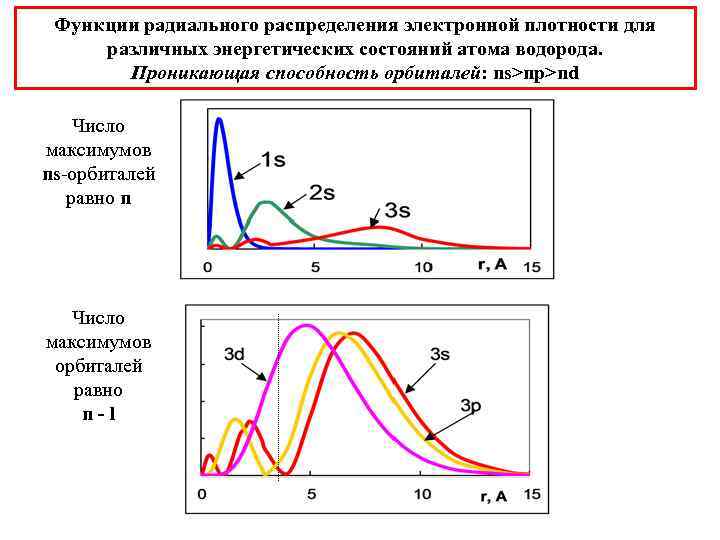
Функции радиального распределения электронной плотности для различных энергетических состояний атома водорода. Проникающая способность орбиталей: ns>np>nd Число максимумов ns-орбиталей равно n Число максимумов орбиталей равно n-l

1. 7 Многоэлектронный атом (одноэлектронное приближение - водородоподобная система) Zэ +Z -(Z-1) ē Zэ = Z - n, l Z – заряд ядра Zэ - эффективный заряд ядра n, l - константа экранирования

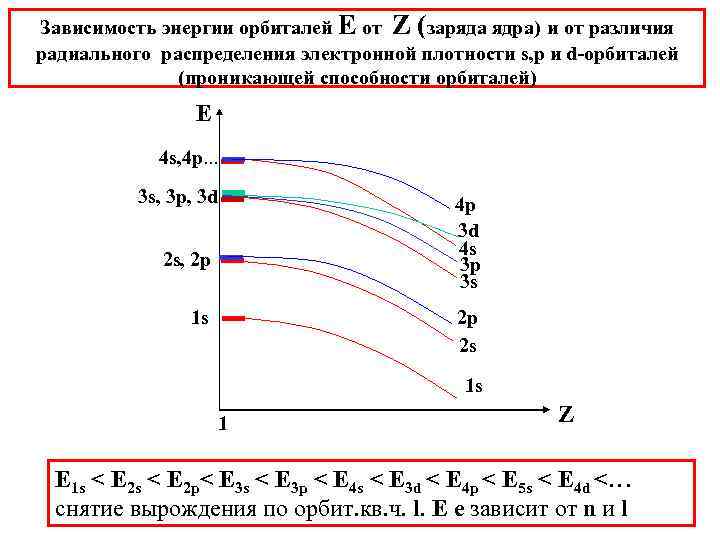
Зависимость энергии орбиталей Е от Z (заряда ядра) и от различия радиального распределения электронной плотности s, p и d-орбиталей (проникающей способности орбиталей) Е 4 s, 4 p. . . 3 s, 3 p, 3 d 4 p 3 d 4 s 3 p 3 s 2 s, 2 p 2 p 2 s 1 s 1 s 1 Z E 1 s < E 2 p< E 3 s < E 3 p < E 4 s < E 3 d < E 4 p < E 5 s < E 4 d <… снятие вырождения по орбит. кв. ч. l. E e зaвисит от n и l

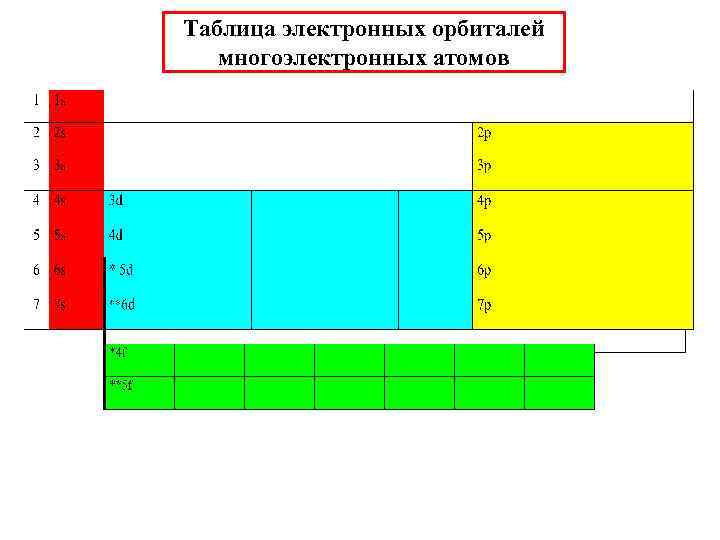
Таблица электронных орбиталей многоэлектронных атомов

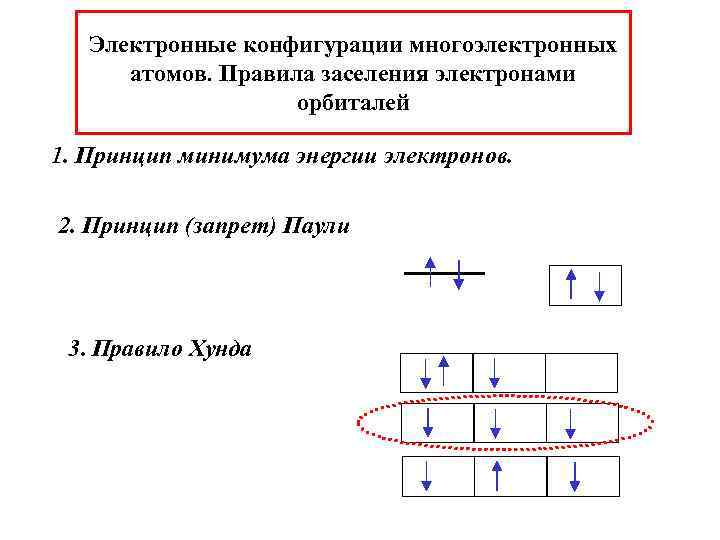
Электронные конфигурации многоэлектронных атомов. Правила заселения электронами орбиталей 1. Принцип минимума энергии электронов. 2. Принцип (запрет) Паули 3. Правило Хунда

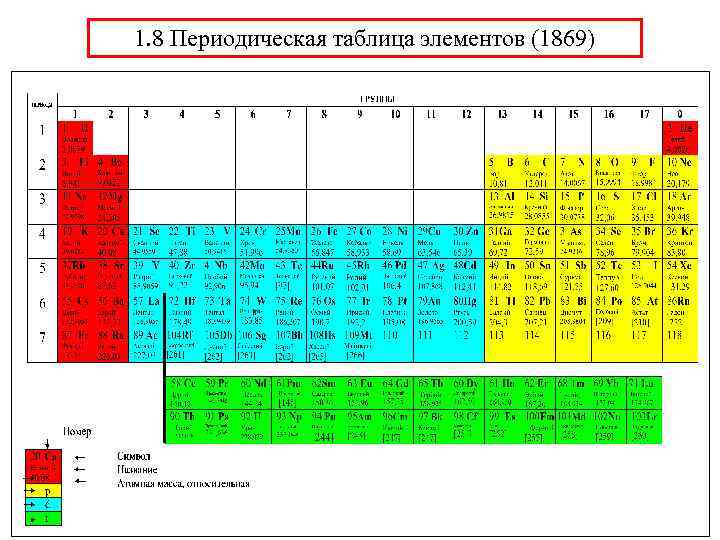
1. 8 Периодическая таблица элементов (1869)

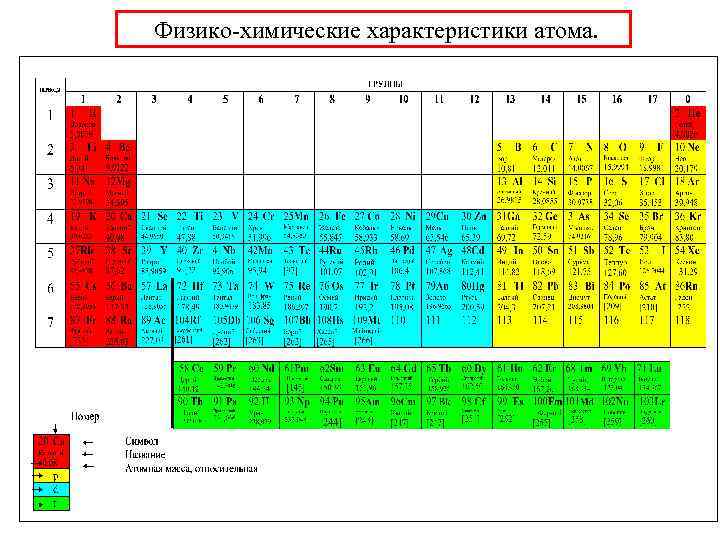
Физико-химические характеристики атома. • Радиус атома и иона K Li Rb Na Ne Ar Kr

Ковалентный радиус ( RA = rсв /2) и радиус иона

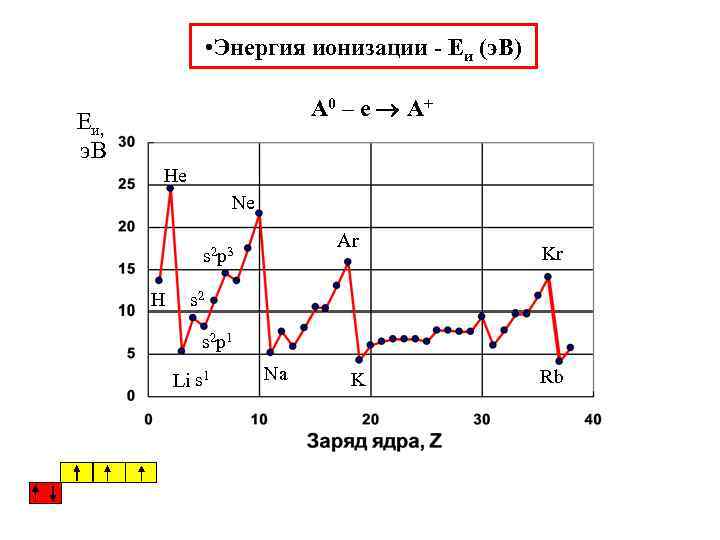
• Энергия ионизации - Eи (э. В) А 0 – е А+ Eи, э. В He Ne Ar s 2 p 3 Н Kr s 2 p 1 Li s 1 Na K Rb

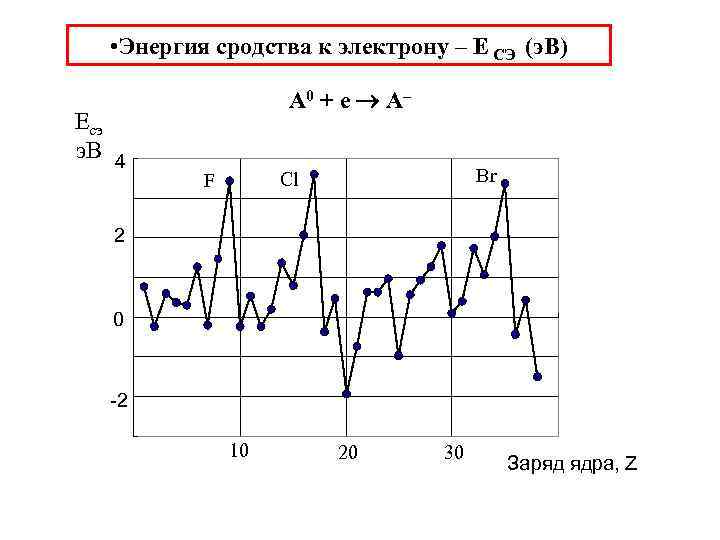
• Энергия сродства к электрону – Е СЭ (э. В) Eсэ э. В 4 A 0 + e A– Br Cl F 2 0 -2 10 20 30 Заряд ядра, Z

• Электроотрицательность (способность атома притягивать к себе элетронную плотность при образовании хим. связи с другим атомом) • по Малликену (э. В) • Шкала Олреда-Рохова • по Полингу F = 1. 0, F = 4. 0 (у. е. )

Химия — теоретические основы Анатолий Анатольевич БАРУНИН —