Химическое равновесие в гомогенных и гетерогенных системах

Химическое равновесие в гомогенных и гетерогенных системах n В аналитической химии используют состояние химического равновесия и величины его характеризующие. n Ни одна химическая реакция не протекает до конца. В ходе реакции устанавливается состояние равновесия, при котором в системе в тех или иных количествах присутствуют все участвующие в реакции вещества. n Химические равновесия, локализованные в одной фазе, называются гомогеными равновесиями. В противоположность этому, когда образуется вторая фаза (например, осадок) или вещества распределяются между двумя или более сосуществующими фазами, имеет место гетерогенное равновесие.

Химическое равновесие в гомогенных и гетерогенных системах n При описании всех видов химических равновесий ключевое значение имеет понимание ряда термодинамических понятий: свободная энергия G (называемая также энергией Гиббса), энтальпия H (тепловое содержание) и энтропия S (мера хаотичности, неупорядоченности системы). При условии постоянства температуры и давления изменение свободной энергии ΔG = ΔH - TΔS характеризует возможность (ΔG < 0) или невозможность (ΔG > 0) самопроизвольного протекания процесса. n В состоянии равновесия в химической системе ΔG =0.

Химическое равновесие в гомогенных и гетерогенных системах n В химическом анализе под состоянием равновесия понимают не состояние покоя, а устойчивое динамическое состояние, при котором обе реакции (прямая и обратная) протекают с одной и тоже скоростью

Химическое равновесие в гомогенных и гетерогенных системах n a. A + b. B ↔ c. C + d. D n ν 1 = k 1 [A]a [B]b - скорость прямой реакции. n ν 2 = k 2 [C]с [D]d – скорость обратной реакции. n В состоянии равновесия ν 1 = ν 2; k 1 [A]a [B]b = k 2 [C]с [D]d. k 1 [C]с [D]d n Kс = —————( константа равновесия). k 2 [A]a [B]b Прямое направление реакции (K > 1). Обратное направление реакции (K<1).

Закон действующих (действия) масс Гульдберга - Вааге (1864 -1867 гг. ) n Гульдберг Като Максимилиан (1836 - 1902) – норвежский физикохимик и математик, член Норвежской АН. n Вааге Петер (1833 - 1900) - норвежский физикохимик и минералог, член Норвежской АН. n «Для идеальных систем в состоянии химического равновесия отношение произведений концентраций продуктов реакции в степенях, равных стехиометрическим коэффициентам, к произведению концентраций исходных веществ в степенях, равных стехиометрическим коэффициентам, есть величина постоянная при данной температуре, давлении и в данном растворителе»

Факторы, влияющие на равновесие в реальных системах ■ a. A + b. B ↔ c. C + d. D ac. C ad. D ■ K = —————; a. А = f. A × [A] aa. A ab. B ■ Коэффициенты активности (f) играют роль поправок на межионные взаимодействия. В очень разбавленных растворах (< 10 -4 M) fi практически равны единице, а аi = [A].

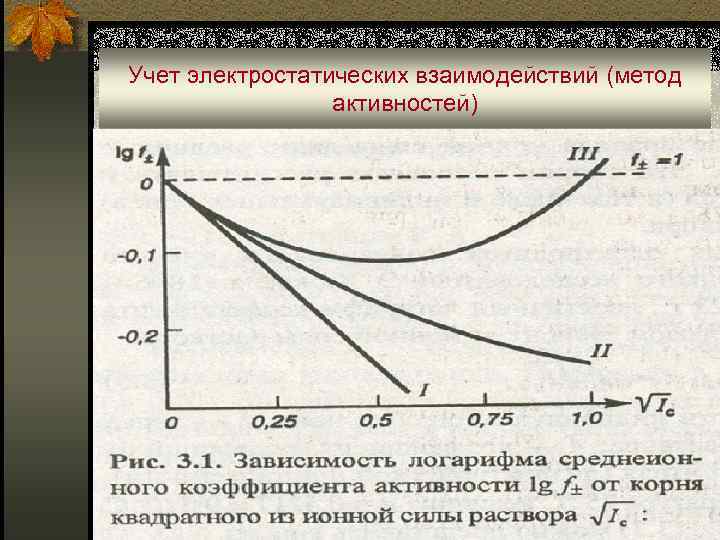
Учет электростатических взаимодействий (метод активностей) ■ На величину f(Х) влияет общая концентрация всех ионов в растворе. В связи с этим Г. Льюис (1907 г. ) ввел понятие ионной силы раствора электролита. ■ Ионная сила раствора (μ) – величина, характеризующая интенсивность электростатического поля всех ионов в растворе, которая равна полусумме произведений молярной концентрации (Сi) каждого иона на квадрат его заряда (zi): μ = ½ ∑ Ci. Zi 2 ■ В 1923 г. Дебай и Хюккель вывели теоретическое выражение для расчета f(Х). Это выражение, известное как уравнение Дебая-Хюккеля, выглядит в упрощенном виде так:

Учет электростатических взаимодействий (метод активностей) n Для высоких значений ионной силы предложено множество эмпирических уравнений. Чаще всего используется уравнение в модификации Дэвиса: n Ионная сила плазмы крови человека равна 0, 15 М, поэтому физиологический раствор – простейший заменитель плазмы крови – должен иметь соответствующую концентрацию Na. CI (0, 15 M, или 0, 9 %).

Учет электростатических взаимодействий (метод активностей)

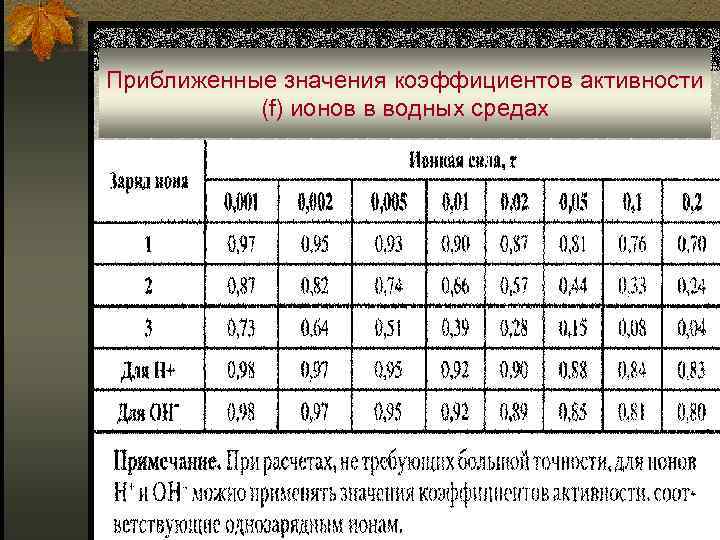Приближенные значения коэффициентов активности (f) ионов в водных средах

Конкурирующие реакции n Компоненты системы могут участвовать одновременно в нескольких равновесиях. n В этих условиях одну из реакций обычно рассматривают в качестве главной, а остальные – в качестве побочных (конкурирующих). n В результате протекания конкурирующих реакций вещества (частицы) распределяются между множеством химических форм. n Концентрацию отдельной формы в состоянии равновесия называют равновесной, а сумму концентраций соответствующих равновесных форм – общей или аналитической концентрацией.

Конкурирующие реакции n Характеристикой глубины протекания конкурирующих реакций служат α – коэффициенты: [A] αA = ——— , CA где [A] – равновесная концентрация; CA – общая (аналитическая) концентрация. a. A = f. A × [A] = f. A× αA× CA

Протолитические конкурирующие реакции n (NH 4)2 CO 3 + Ca. CI 2 = Ca. CO 3 ↓ + 2 NH 4 Cl (главная реакция). n СO 32 - + H 2 O ↔ HCO 3 - + OH- HCO 3 - + H 2 O ↔ H 2 CO 3 + OH- (конкурирующие реакции). n Для нахождения α (СO 32 - ) проводим следующие расчеты. n C (СO 32 -) = [CO 32 -] + [HCO 3 -] + [H 2 CO 3] (уравнение материального баланса).

Протолитические конкурирующие реакции n Через соответствующие константы кислотности найдем [HCO 3 -] и [H 2 CO 3]: [H 3 O+] [HCO 3 -] n H 2 CO 3 + H 2 O ↔ HCO 3 - + H 3 O+ ; Kα 1 = ———————. [H 2 CO 3] [CO 32 -] [H 3 O+] n HCO 3 - + H 2 O ↔ CO 32 - + H 3 O+ ; Kα 2 = ——————. [HCO 3 -]

Протолитические конкурирующие реакции [CO 32 -] [H 3 O+] n Отсюда [HCO 3 -] = ———————. Kα 2 [H 3 O+]2 [CO 32 -] n [H 2 CO 3] = ————. Kα 1 • Kα 2 [CO 32 -] [H 3 O+]2 [CO 32 -] n Тогда C (СO 32 - ) = [CO 32 -] + ——————. Kα 2 Kα 1 • Kα 2

Протолитические конкурирующие реакции n Далее: [H 3 O+]2 n С(CO 32 -) = [CO 32 -] ( 1 + ————— ) = Kα 2 Kα 1 • Kα 2 Kα 1 • Kα 2 + Kα 1 [H 3 O+] + [H 3 O+]2 n [CO 32 -] × [ ——————————] Kα 1 • Kα 2 Kα 1 • Kα 2 n Отсюда α(CO 32 - ) = ————————— Kα 1 • Kα 2 + Kα 1 [H 3 O+] + [H 3 O+]2

α – коэффициенты в протолиметрии [H+]n n αHn. A = —————————————. Kα, 1 Kα, 2 … Kα, n + Kα, 1 Kα, 2 … Kα, n-1[H+] +…. . + [H+]n Kα, 1 Kα, 2 … Kα, n- α An- = —————————————. Kα, 1 Kα, 2 … Kα, n + Kα, 1 Kα, 2 … Kα, n-1[H+] + …+ [H+]n a. А = f А × α А × C А

Протолитические конкурирующие реакции n Задача. n Оценить возможность реакции 1, 25 × 10 -3 М (NH 4)2 CO 3 + 0, 01 М Ca. CI 2 = Ca. CO 3 ↓ + 2 NH 4 Cl при р. Н 6. 00. n ПР (Ca. CO 3 ↓) = 2. 88× 10 -9. Следовательно, [Ca 2+]×[CO 32 -] > ПР (Ca. CO 3 ↓). n [CO 32 -] = С(CO 32 -)× α(CO 32 -).

α – коэффициенты в реакциях комплексообразования n 0, 01 М Ag(NO 3) + 0, 01 М Na. CI ↔ Ag. CI↓ + Na. NO 3 (основная реакция) n Ag(NO 3) + NH 3 ↔ Ag(NH 3)+ (конкурирующая реакция) n Ag(NH 3)+ + NH 3 ↔ Ag(NH 3)2+ (конкурирующая реакция) n ПР(Ag. CI↓) = 1, 78× 10 -10 [Ag+]×[CI-] > ПР(Ag. CI↓ n [Ag+] = С(Ag+)× α(Ag+) n С(Ag+) = [Ag+] + [Ag(NH 3)2+]

α – коэффициенты в реакциях комплексообразования [Ag(NH 3)+] n β[Ag(NH 3)+] = ────. [Ag+]×[NH 3] n [Ag(NH 3)+] = β(Ag(NH 3)+ × [Ag+]×[NH 3]. [Ag(NH 3)2+] n β[Ag(NH 3)2+] = ────. [Ag+]×[NH 3]2 n [Ag(NH 3)2+] = β[Ag(NH 3)2+] × [Ag+]×[NH 3]2.

α – коэффициенты в реакциях комплексообразования n С(Ag+) = [Ag+] + β(Ag(NH 3)+ × [Ag+]×[NH 3] + β[Ag(NH 3)2+] × [Ag+]×[NH 3]2 = [Ag+] (1 + β(Ag(NH 3)+ × [NH 3] + β[Ag(NH 3)2+] × [NH 3]2). n α(Ag+) = [Ag+] / С(Ag+) = 1 = ————————————. (1 + β(Ag(NH 3)+×[NH 3] + β[Ag(NH 3)2+]×[NH 3]2)

α – коэффициенты в реакциях комплексообразования n 2 М NH 3 1 n α(Ag+) = ——————— ≈ 1, 5 • 10 -8 1 + 2. 09 • 103 • 2 + 1, 62 • 107 • 4 n [Ag+]×[CI-] = 1 • 10 -2 • 1, 5 • 10 -8 = 1, 5 • 10 -12 < ПР(Ag. CI↓).

α – коэффициенты в реакциях комплексообразования n СM = [M] + [ML]2 + … + [ML]n n CL = [L] + [ML] + 2 [ML]2 + … +n [ML]n [ML]2 [ML]n n β 1= ————; β 2= ————; βn= ————; [M] [L]2 [M] [L]n n СM = [M](1 + β 1 [L] + β 2 [L]2 + βn [L]n); [M] 1 n αM = ————————; СM (1 + β 1 [L] + β 2 [L]2 + βn [L]n)

Константы равновесия n αA = [A] • f. A = CA • αA • f. A; n a. A + b. B ↔ c. C + d. D; a. Cc • a. Dd [C]C • [D]d CCc • CDd n Kт = —————; Kc = —————; Kу = —————; a. Aa • a. Bb [A]a • [B]b CAa • CBb [C]c • [D]d f c • f d C c • C d α c • α d C D C D n Kт = ──────×────= Kc × ────= —————× [A]a • [B]b f. Aa • f. Bb CAa • CBb αAa • αBb f. Cc • f. Dd αCc • αDd f. Cc • f. Dd ────= Kу ×————× ────. f. Aa • f. Bb αAa • αBb f. Aa • f. Bb

Кислотно-основное равновесие n Николя Лемери, аптекарь из Парижа (1645 -1715): «Кислоты – соединения с острыми шипами. Основания – соединения с порами. Шипы кислот проникают в поры оснований. n Антуан Лоран Лавуазье (1743 -1794): «Кислоты-комбинации радикалов и кислорода. Основания-комбинации металлов и кислорода» . n Хэмфри Дэви (1778 -1850): «Кислотные свойства веществ обусловлены наличием водорода» . n Сванте Август Аррениус (1859 -1927): «Кислоты-вещества, образующие при диссоциации в водном растворе ионы H+, а основания – ионы ОН-» .

Теория кислот и оснований Аррениуса

Теории кислот и оснований n Датский физико-химик Йоханнес Николаус Бренстед (1879 - 1947), английский химик Томас Мартин Лоури (1874 -1936). n Теория Бренстеда-Лоури (1923 г. ): «Кислота – вещество, выделяющее при ионизации протоны, а основание – вещество, присоединяющее протоны» ; «Вещества, способные как присоединять, так и отдавать протоны, называются амфолитами» . n Кислоты и основания находятся в протолитическом равновесии: HB ↔ H+ + B- HB – кислота, сопряженная с основанием B- - основание, сопряженное с кислотой НВ.

Примеры кислот и оснований по теории Бренстеда - Лоури

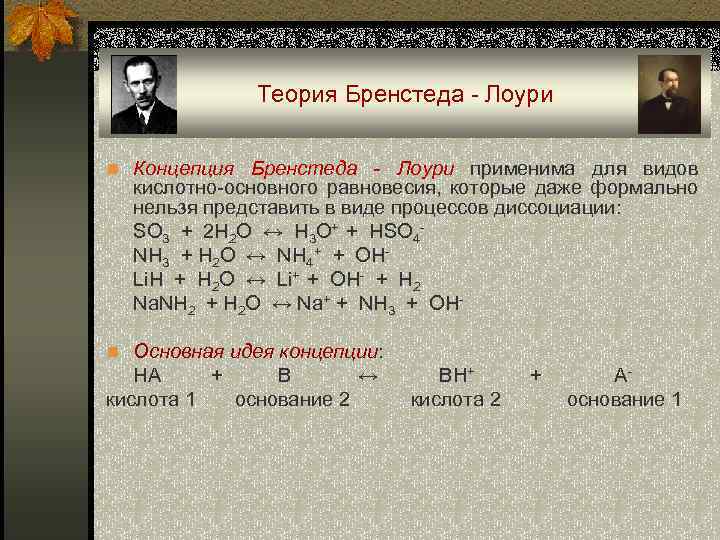Теория Бренстеда - Лоури n Концепция Бренстеда - Лоури применима для видов кислотно-основного равновесия, которые даже формально нельзя представить в виде процессов диссоциации: SO 3 + 2 H 2 O ↔ H 3 O+ + HSO 4 - NH 3 + H 2 O ↔ NH 4+ + OH- Li. H + H 2 O ↔ Li+ + OH- + H 2 Na. NH 2 + H 2 O ↔ Na+ + NH 3 + OH- n Основная идея концепции: HA + В ↔ ВН+ А- кислота 1 основание 2 кислота 2 основание 1

Теории кислот и оснований n Гилберт Ньютон Льюис (1875 -1946); n Теория кислот и оснований Льюиса (1926 г. ): «Кислота- соединение, способное принять электронную пару с образованием ковалентной связи, а основание - соединение, способное предоставить электронную пару для образования ковалентной связи» :

Теории кислот и оснований n Советский физикохимик Михаил Ильич Усанович (1894 - 1981); n Теория кислот и оснований Усановича: «Кислоты выделяют катионы и взаимодействуют с анионами или электронами; основания отдают анионы или электроны, которые соединяются с электронами» : SOCI 2 + Na 2 SO 3 ↔ 2 Na. CI + 2 SO 2 SOCI 2 ↔ SO 2+ + 2 CI- кислота Na 2 SO 3 ↔ 2 Na+ + SO 32 - основание SO 2+ + SO 32 - ↔ 2 SO 2 2 Fe 3+ + Sn 2+ ↔ 2 Fe 2+ + Sn(IV)

Теория Бренстеда - Лоури n Главная особенность теории – учет роли растворителя в кислотно-основном равновесии: HB + S ↔ HS+ + B- n Апротонные растворители, не обладающие ни кислотными, ни основными свойствами (бензол, гексан, хлороформ); n Протофильные растворители, обладающие только основными свойствами (NH 3, N 2 H 2, NH 2 OH, C 5 H 5 N, диоксан, диэтиловый эфир); n Протогенные растворители, обладающие только кислотными свойствами (HCI, HBr, CH 3 COOH, C 6 H 5 COOH); n Амфипротные растворители, обладающие как кислотными, так и основными свойствами (вода, спирты, первичные и вторичные амины, карбоновые кислоты).

Амфипротные растворители n Важнейшая особенность амфипротных растворителей – способность к передаче протона от одной молекулы к другой: 2 SH ↔ S- + SH 2+ (автопротолиз); n Константа автопротолиза: Kт. SH = as- • a. SH+ (SH 2+ - ион лиония; S- - ион лиата); n Соотношение активностей лиония и лиата определяет реакцию среды:

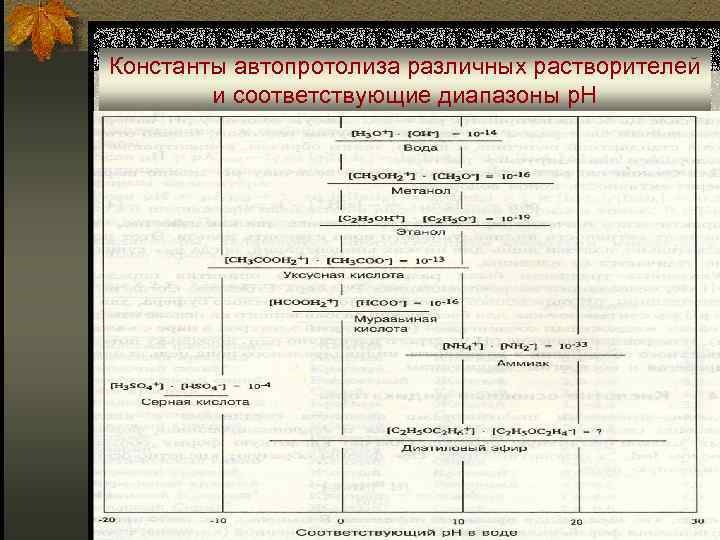Константы автопротолиза различных растворителей и соответствующие диапазоны р. Н

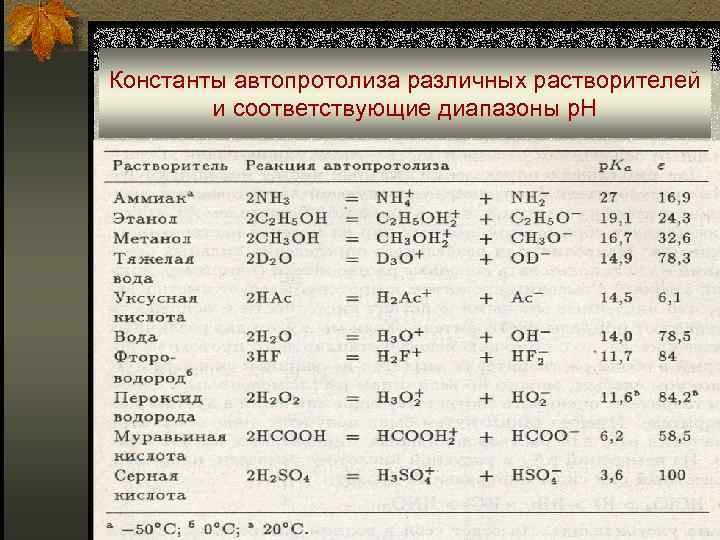Константы автопротолиза различных растворителей и соответствующие диапазоны р. Н

Константа автопротолиза воды n Kw = a. H 3 O+ • a OH- (a. H+ • a. OH- ) - константа автопротолиза или ионное произведение воды = 1, 008 • 10 -14 ~ 1, 0 • 10 -14 (25 0 C); n Ион H 3 O+ по номенклатуре IUPAC называют ионом оксония. В отечественной литературе употребляют название гидроксоний.

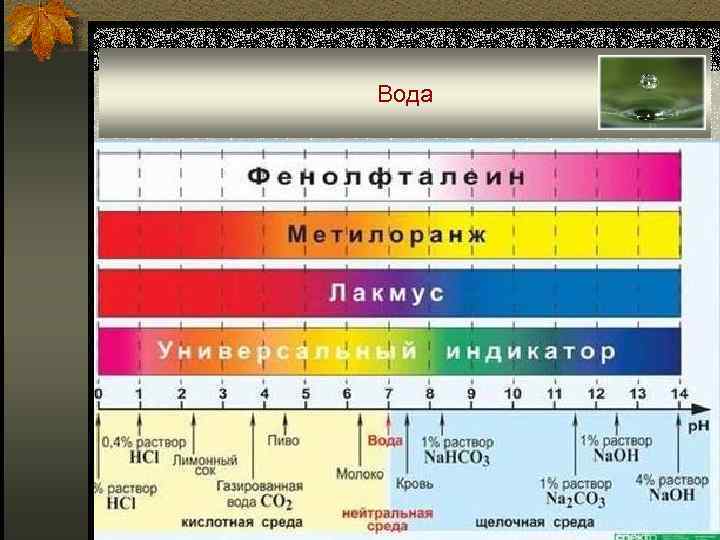Вода

Сила кислот и оснований в водных растворах n Сила кислот и оснований характеризуется соответствующими константами равновесий: кислотности (Kaт), основности (Kbт); a. BH+ • a. S- n B + HS ↔ S- + BH+; Kbт = ————— a. B a SH 2+ • a. A- n HA + HS ↔ SH 2+ + A-; Kaт = —————; a. HA n Kaт • Kbт = KSHт Чем сильнее кислота, тем слабее сопряженное основание

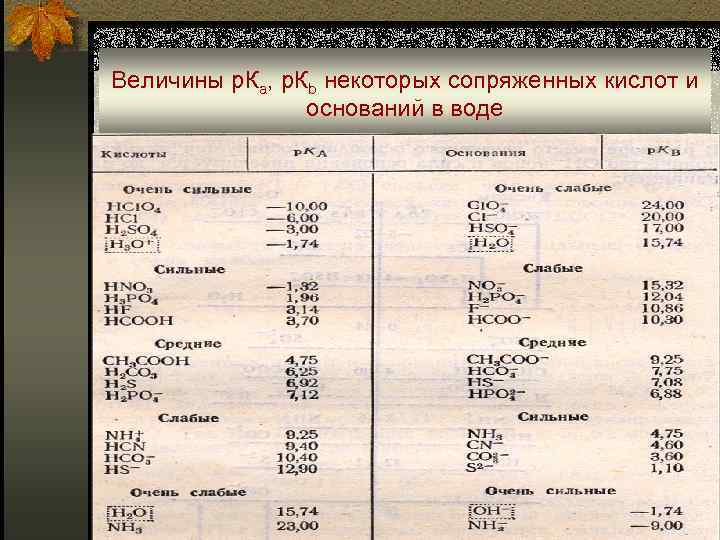Величины р. Ка, р. Кb некоторых сопряженных кислот и оснований в воде

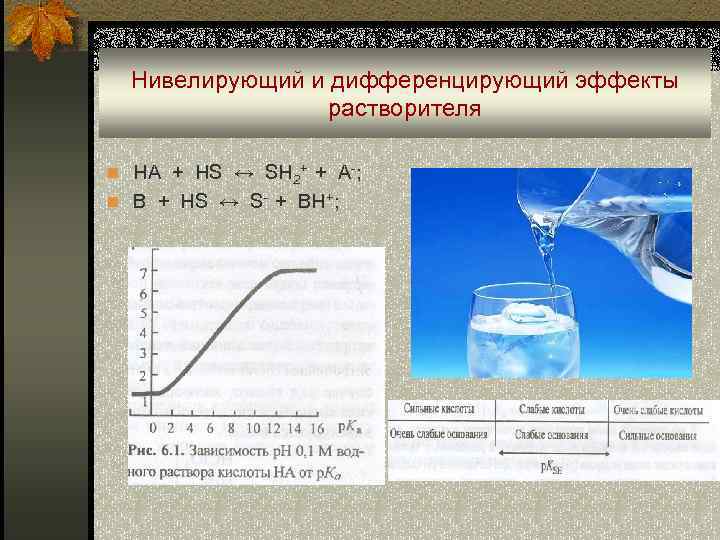Нивелирующий и дифференцирующий эффекты растворителя n HA + HS ↔ SH 2+ + A-; n B + HS ↔ S- + BH+;

Нивелирующий эффект растворителя

Нивелирующий эффект растворителя

Дифференцирующий эффект растворителя n HCIO 4 > HBr > H 2 SO 4 > HCI > HNO 3 (среда СН 3 СOOH). n C 6 H 5 COOH + H 2 O ↔ C 6 H 5 COO- + H 3 O+ (слабая кислота). n C 6 H 5 COOH + NH 3 ↔ C 6 H 5 COO- + NH 4+ (сильная кислота). n C 6 H 5 COOH + H 2 SO 4 ↔ C 6 H 5 COOH 2 + + HSO 4 - (слабое основание). n Кислоты: HCIO 4 ~ HBr ~ H 2 SO 4 ~ HCI ~ HNO 3 (H 2 O). n p. Ka: 5, 8 6, 4 8, 2 8, 9 9, 4 (CH 3 COOH). n p. Ka: 3, 2 4, 0 5, 4 4, 3 (пиридин). n Дифференцирующее действие растворителей зависит от индивидуальных свойств веществ и не ограничивается протонно-донорно-акцепторными взаимодействиями.

Сила кислот в неводных растворах (ионизация) (диссоциация) n HA + SH ↔ SH 2+A- ↔ SH 2+ + A- ; [SH 2+A-] [SH 2+][A-] n Kион = ————; Kдис = —————; [HA] [SH 2+A-] [SH 2+][A-] Kион • Kдис n Ка = —————— = —————; [HA]+[SH 2+A-] CHA 1 + Kион В водных растворах значения Ка совпадают с Kдис.

Сила оснований в неводных растворах (ионизация) (диссоциация) n B + SH ↔ BH+S- ↔ BH+ + S-; [BH+S-] [BH+][S-] n Кион = ————; Kдис = —————; [B] [BH +S-] [BH+][S-] Kион • Kдис n Kb = —————— = —————; [B] + [BH+S-] CB 1 + Kион В водных растворах значения Кb совпадают с Kдис.

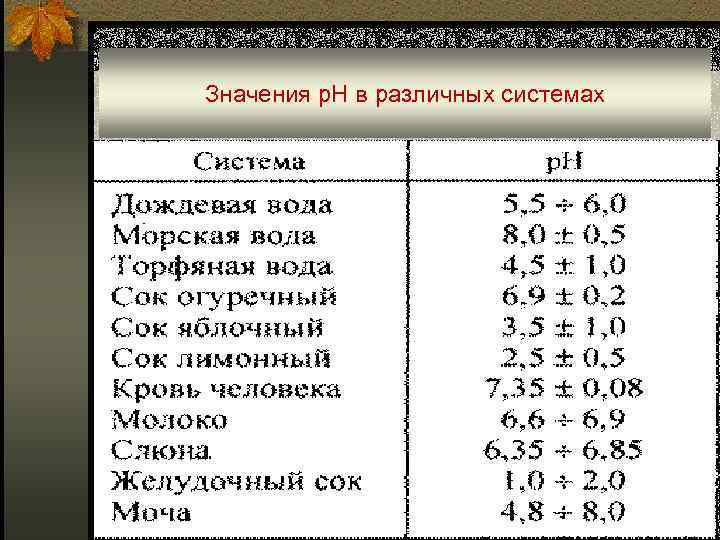Значения р. Н в различных системах

Буферные системы n Буферными называют системы, поддерживающие определенное значение какого-либо параметра при изменении состава: кислотно-основные – p. H; окислительно-восстановительные – E; металлобуферные – p. M; Буферная система, как правило, представляет собой cопряженную пару. Природная буферная система – кровь: CO 2 • H 2 O / HCO 3¯, амфотерные белки плазмы – p. H = 7, 4; n Кислотно-основные буферные системы: слабая кислота и ее соль (CH 3 COOH + CH 3 COO‾ ) – кислотная;

Кислотно-основные буферные системы n Кислотно-основные буферные системы: слабое основание и его соль (NH 3 + NH 4+) – основная; индивидуальные химические соединения (KH 2 PO 4+ K 2 HPO 4) – кислая. n Между компонентами буферной системы и растворителем возможны взаимодействия, в результате которых образуются исходные компоненты буферной системы. Таким образом, поддерживается относительное постоянство их концентраций: HA + H 2 O ↔ H 3 O+ + A- (I) A- + H 2 O ↔ HA + OH- (II) ■ При добавлении сильных протолитов последние за счет взаимодействия с компонентами буферной системы превращаются в слабые: HA + OH- ↔ H 2 O + A- (III) A- + H 3 O+ ↔ HA + H 2 O (IV)

Основные характеристики кислотно-основных буферных систем n Уровень р. Н - значение р. Н, на котором поддерживается постоянство этой величины. n Диапазон р. Н буферирования (нижняя и верхняя границы p. H). n Буферная емкость (β) - число молей эквивалентов сильного протолита, которые нужно добавить к 1 л раствора, чтобы изменить p. H раствора на единицу. n Расчет р. Н кислотно-основных буферных растворов. Константа равновесия (I) является константой кислотности HA: [H 3 O+][ A-] [HA] n Ka = ——————; [H 3 O+] = Ka ————; [HA] [ A -]

Основные характеристики кислотно-основных буферных систем n Расчет р. Н кислотно-основных буферных растворов (уравнение Гендерсона-Хассельбаха). Поскольку равновесия (I, II) в значительной степени сдвинуты влево, можно в первом приближении считать, что [HA] ≈ CНА и [A-] = CA-, поэтому CНА CA- [H 3 O+] = Ka ———; р. Н = р. Ка + Ig ———; CA- CНА Cосн В общем случае: р. Н = р. Ка + Ig ———; Скисл

Основные характеристики кислотно-основных буферных систем n Диапазон р. Н буферирования (∆ p. H) зависит от соотношения Cосн : Скисл, которое обычно находится в диапазоне 0, 1 – 10. Тогда ∆р. Н = р. Ка ± 1(кислотная система); ∆р. Н = р. Кb ± 1(основная система); n Буферная емкость (β): d. COH- d. CH 3 O+ β = ——— и β = - ————; dp. H Сильные протолиты (OH-, Н 3 О+) при попадании в буферный раствор превращаются в слабые протолиты – компоненты буферного раствора А- и НА соответственно. Тогда d. COH- = d. CA- и d. CH 3 O+ = d. CHA

Буферная емкость (β) d[A-] d[A-] n —— = ————— = -2, 3 ————— = - 2, 3[H 3 O+] ————; dp. H d(-Ig[H 3 O+]) d(In[H 3 O+]) d[H 3 O+] [HA] Выразим [H 3 O+] = Ka ———; Суммарная концентрация [ A -] буф. системы С = [HA] + [ A-]; С - [ A -] С Тогда [H 3 O+] = Ka ——— = Ka ( —— - 1); [ A -] [ A-] C d[A-] [ A-]2 1 d[H 3 O+] = - Ka —— d[ A-]; ———— = - —— • ———; [ A-]2 d[H 3 O+] C Ka

Буферная емкость (β) - [ A ]2 1 [HA] [ A ]2 1 n β = 2, 3 [H 3 O+] • —— = 2, 3 Ka —— • —— ; C K a [A-] C Ka [HA] [A-] β = 2, 3 ————— (1); [HA] + [A-] ■ β можно связать с другим параметром системы – Ка: [H 3 O+] [A-] C • Ka = ————— = —————; [A-] = —————— ; [HA] C - [A-] Ka + [H 3 O+]

Буферная емкость (β) d[A-] d[A -] n —— = ————— = -2, 3 ————— = - 2, 3[H 3 O+] ————; dp. H d(-Ig[H 3 O+]) d(-In[H 3 O+]) d[H 3 O+] d[A-] C • Ka C • Ka ■ ——— = - ——————; β = 2, 3[H 3 O+] —————— (2); d[H 3 O+] (Ka + [H 3 O+])2 (Ka + [H 3 O+])2 ■ Буферная емкость полезна для расчета изменения р. Н в системе при добавлении сильных протолитов и состава буферной смеси: ∆p. H = ∆Cкисл / β = ∆Cосн / β (3)

Буферная емкость (β) n Пример (Ю. А. Золотов и др. Основы аналитической химии. Кн. 1. М. : Высш. шк. , 2004. - с. 133): Аммонийная буферная система 0, 1 М NH 3 и 0, 2 М NH 4 CI (p. H = 8, 96): ■ расчет β по уравнениям (1, 2) β = n Расчет изменения р. Н при добавлении к 1 л р-ра 1 • 10 -2 М HCI ∆p. H =

Буферная емкость (β) n p. H раствора после введения HCI составил 8, 96 – 6, 7 • 10 -2 = 8, 89; n Определение состава аммонийной буферной смеси с р. Н 9, 25 ([H 3 O+] = 5, 6 • 10 -10), при добавлении к 0, 5 л которого 25 ммоль Na. OH значение р. Н изменяется не более чем на 0, 05: находим β = 25 • 10 -3 / (0, 5 • 0, 05) = 1; Подставляя Ка = 5, 7 • 10 -10 в ур-ние (2), находим С: находим соотношение CNH 4+ / CNH 3:

Буферная емкость (β) n Пример: требуется приготовить буферный раствор с р. Н =10 и β = 0, 2. n Решение: по справочнику подбираем подходящую буферную систему NH 3 + NH 4 с р. Ка = 9, 25. Выразим равновесные концентрации [NH 3] и [NH 4] через α- коэффициенты С • αNH 3 • C • αNH 4+ β = 2, 3 • ——————— = 2, 3 • C • αNH 3 • αNH 4+; отсюда C С = β /2, 3 • αNH 4+; αNH 3, αNH 4+ находим по известным уравнениям

Буферная емкость (β) n Пример (продолжение): Ка, NH 4+ [H 3 O+] αNH 3 = ——————— = 0, 863; αNH 4+ = ——————— = 0, 137; [H 3 O+] + Ка, NH 4+ 0, 2 C = ——————— = 0, 735 M; CNH 3= 0, 735 • 0, 863 = 0, 634 M; 2, 3 • 0, 137 • 0, 863 CNH 4+ = 0, 735 • 0, 137 = 0, 101 M;

Буферная емкость (β) n Буферная емкость зависит от суммарной концентрации компонентов и соотношения их концентраций. Максимальная буферная емкость достигается при равенстве концентраций компонентов сопряженной пары: приравнивая первую производную уравнения dβ / d[HA] к нулю, получаем [HA](C - [HA]) 2, 3 {1(C - [HA]) + [HA](0 – 1)} d{2, 3 ——————} / d[HA] = —— • —————— = C d[HA] 2, 3 ([HA] + [A-] - [HA]) 2, 3 ([A-] - [HA]) —— • —————— = —— • —————— C d[HA] C d[HA]

Кислотно-основные буферные системы n Буферная емкость (β). При равенстве концентраций сопряженной пары CA- 0, 5 C • 0, 5 C р. Н = р. Ка + Ig ——; р. Н = р. Ка; βmax= 2, 3 ————— = 0, 575 C; CНА C если р. Н будет > или< р. Ка на 1, βmax= 0, 19 С; ■ Буферные свойства растворов сильных протолитов: сопряженные системы Н 3 О+ / Н 2 О (сильные кислоты); OH- / Н 2 О (сильные основания); поэтому β = 2, 3 [Н 3 О+] – для сильных кислот и β = 2, 3 [ОН-] – для сильных оснований

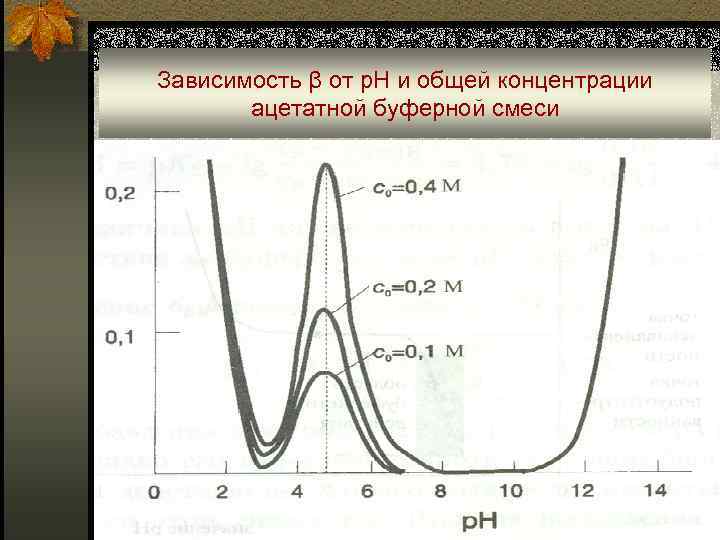Зависимость β от р. Н и общей концентрации ацетатной буферной смеси

Кислотно-основные буферные системы

Буферные системы организма человека n Основными буферными системами организма человека являются: гидрокарбонатная, гемоглобиновая, фосфатная и белковая. n Гидрокарбонатная буферная система образована оксидом углерода (IV), взаимодействие которого с водой приводит к равновесной системе: n В этой системе донором протона является H 2 CO 3, а акцептором протона - HCO 3 -.

Буферные системы организма человека n Если в кровь поступает кислота, то происходит реакция с образованием CO 2, который выводится через легкие: H+ + HCO 3 - ↔ H 2 CO 3 ↔ CO 2 + H 2 O n При поступлении в кровь оснований: OH- + H 2 CO 3 ↔ HCO 3 - + H 2 O n Гидрокарбонатный буфер обеспечивает около 55 % всей буферной емкости крови. n Все буферные системы в организме взаимосвязаны.

Буферные системы организма человека

Взаимодействие кислоты и основания n При смешивании кислоты и основания устанавливается равновесие, включающее несколько реакций. «Побеждает» реакция, константа которой больше: