x’ = x(c — (x 2+y 2)) —

x' = x(c - (x2+y2)) - 2πy y' = y(c - (x2+y2)) + 2πx
с = - 1.1 с = - 0.7 с = 0.1 с = 0.1
x' = x(c - (x2+y2)) - 2πy y' = y(c - (x2+y2)) + 2πx
x' = x(c +2(x2+y2) - (x2+y2)2) - 2πy y' = y(c +2(x2+y2) - (x2+y2)2)
с = -0.1 с = 0.1 с = 0.3 с = 0.5 с =
x y x y
x y x y
Скачать презентацию x’ = x(c — (x 2+y 2)) — Скачать презентацию x’ = x(c — (x 2+y 2)) —

bifur_cycle.ppt

  • Количество слайдов: 12

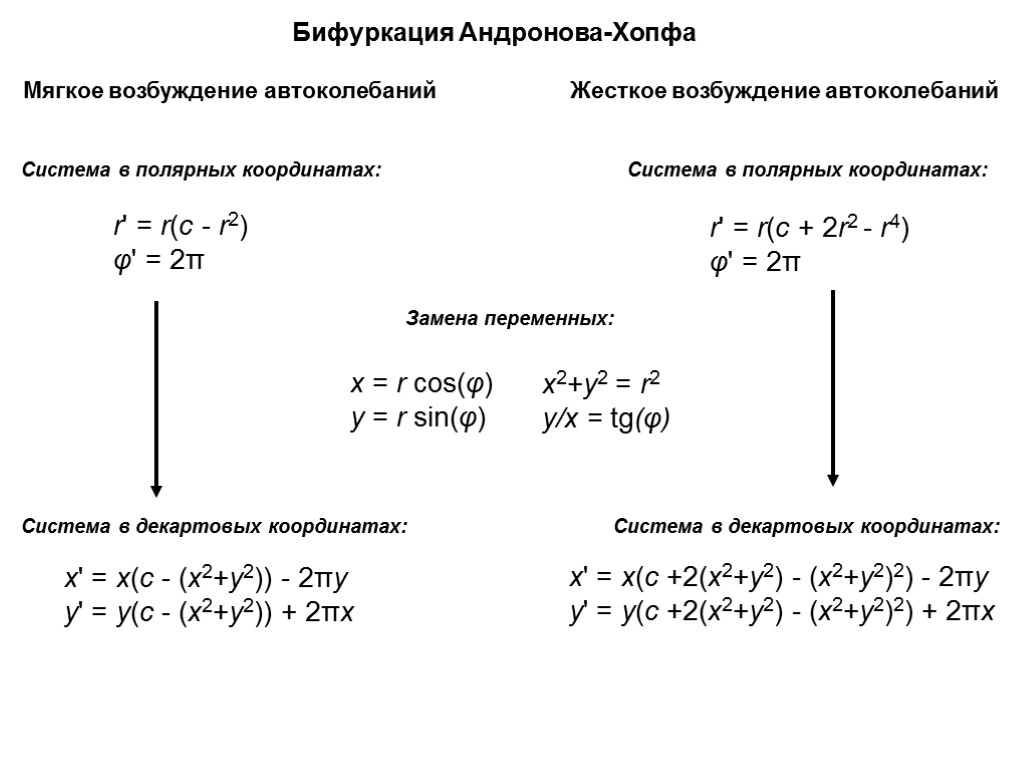
>x' = x(c - (x2+y2)) - 2πy y' = y(c - (x2+y2)) + 2πx x' = x(c - (x2+y2)) - 2πy y' = y(c - (x2+y2)) + 2πx x = r cos(φ) y = r sin(φ) r' = r(c - r2) φ' = 2π Бифуркация Андронова-Хопфа Система в полярных координатах: Система в декартовых координатах: x2+y2 = r2 y/x = tg(φ) Замена переменных: x' = x(c +2(x2+y2) - (x2+y2)2) - 2πy y' = y(c +2(x2+y2) - (x2+y2)2) + 2πx r' = r(c + 2r2 - r4) φ' = 2π Жесткое возбуждение автоколебаний Система в полярных координатах: Система в декартовых координатах: Мягкое возбуждение автоколебаний

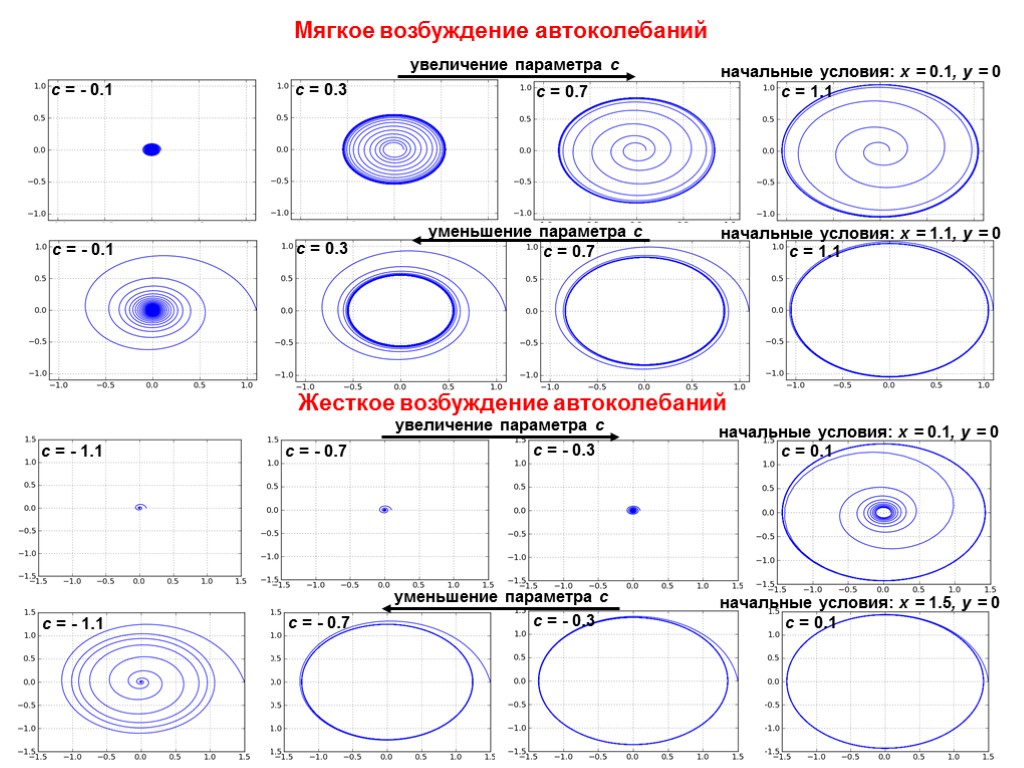>с = - 1.1 с = - 0.7 с = 0.1 с = 0.1 с = - 1.1 с = - 0.7 с = 0.1 с = 0.1 с = - 0.3 с = - 0.3 с = - 1.1 с = - 0.7 увеличение параметра с уменьшение параметра с начальные условия: x = 0.1, y = 0 начальные условия: x = 1.5, y = 0 с = - 0.1 с = 0.3 с = 1.1 с = 0.7 начальные условия: x = 0.1, y = 0 уменьшение параметра с начальные условия: x = 1.1, y = 0 с = - 0.1 с = 0.3 с = 1.1 с = 0.7 Жесткое возбуждение автоколебаний Мягкое возбуждение автоколебаний увеличение параметра с

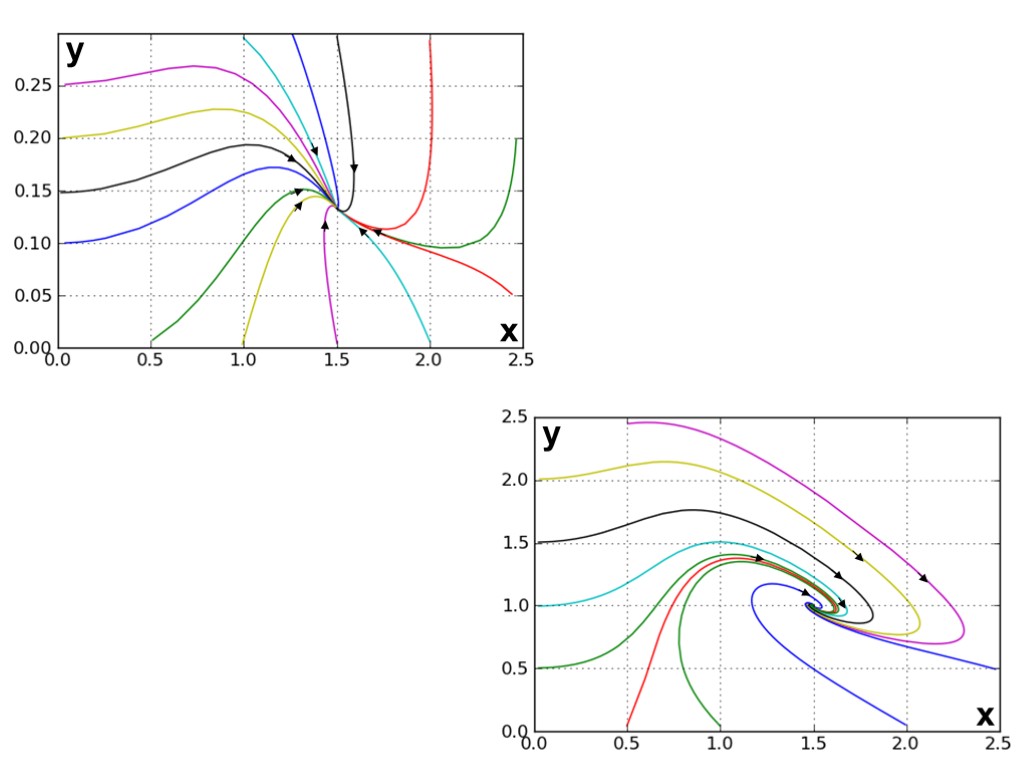
>x' = x(c - (x2+y2)) - 2πy y' = y(c - (x2+y2)) + 2πx x' = x(c - (x2+y2)) - 2πy y' = y(c - (x2+y2)) + 2πx x = r cos(φ) y = r sin(φ) r' = r(c - r2) φ' = 2π Бифуркация Андронова-Хопфа (мягкое возбуждение автоколебаний) Система в полярных координатах: Система в декартовых координатах: x2+y2 = r2 y/x = tg(φ) Стационарные режимы: Замена переменных: y x c = 0.5 y x c = - 0.5

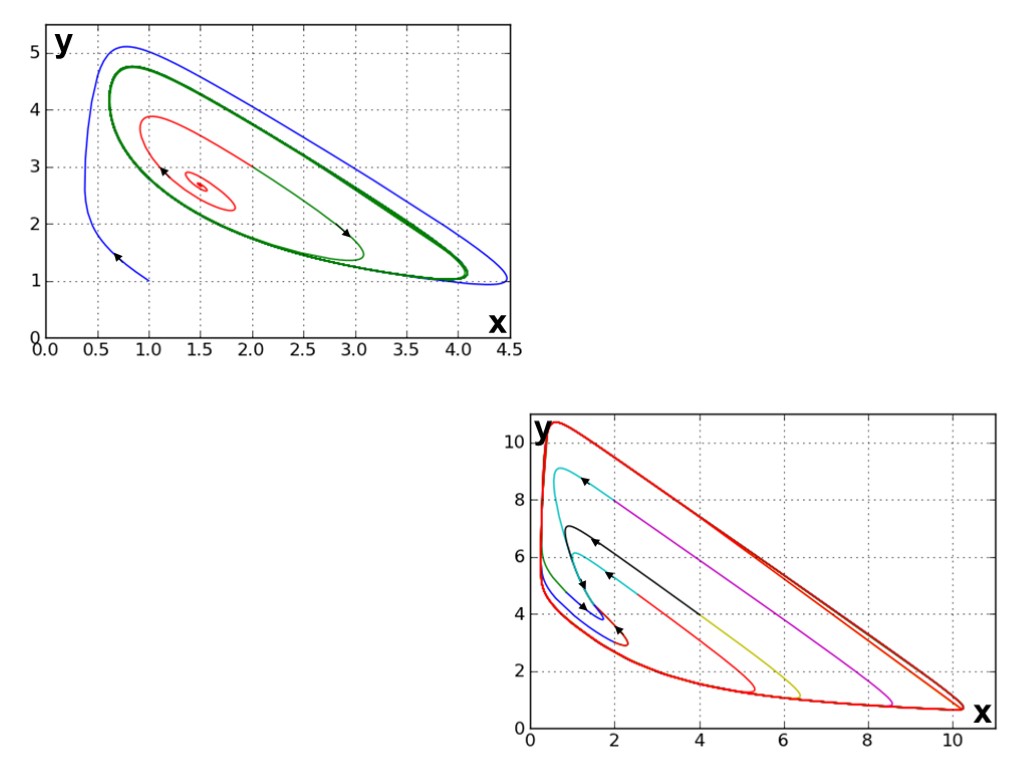
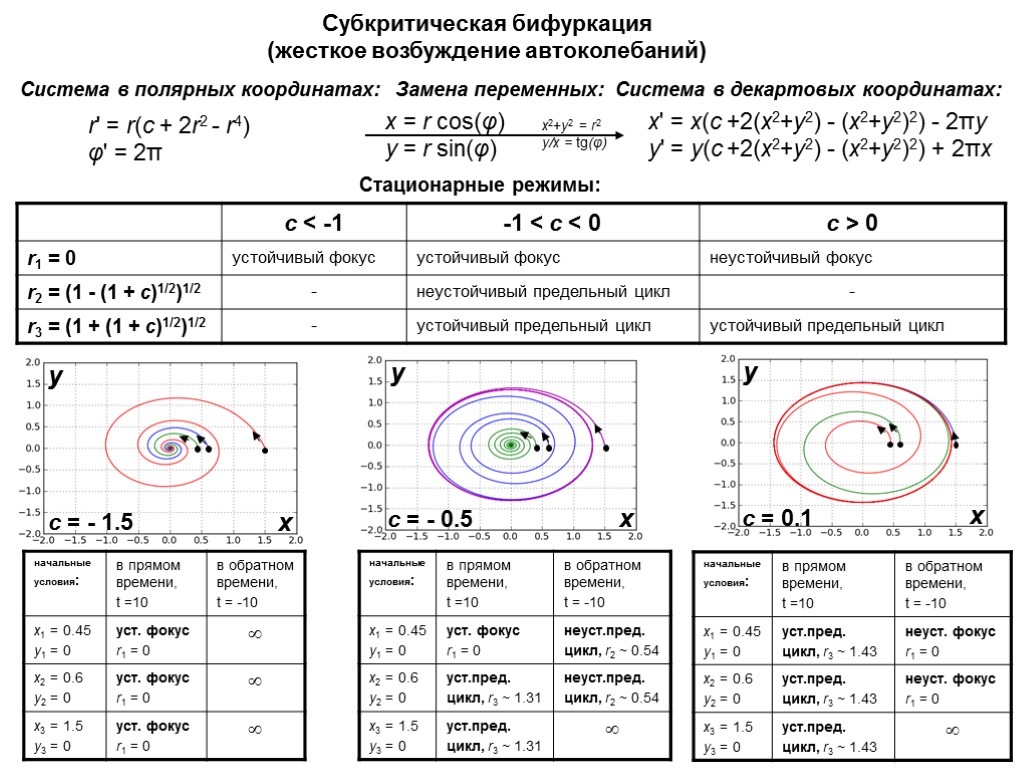>x' = x(c +2(x2+y2) - (x2+y2)2) - 2πy y' = y(c +2(x2+y2) - (x2+y2)2) x' = x(c +2(x2+y2) - (x2+y2)2) - 2πy y' = y(c +2(x2+y2) - (x2+y2)2) + 2πx x = r cos(φ) y = r sin(φ) r' = r(c + 2r2 - r4) φ' = 2π Субкритическая бифуркация (жесткое возбуждение автоколебаний) Система в полярных координатах: Система в декартовых координатах: y y y x x x x2+y2 = r2 y/x = tg(φ) c = - 1.5 c = 0.1 c = - 0.5 Стационарные режимы: Замена переменных:

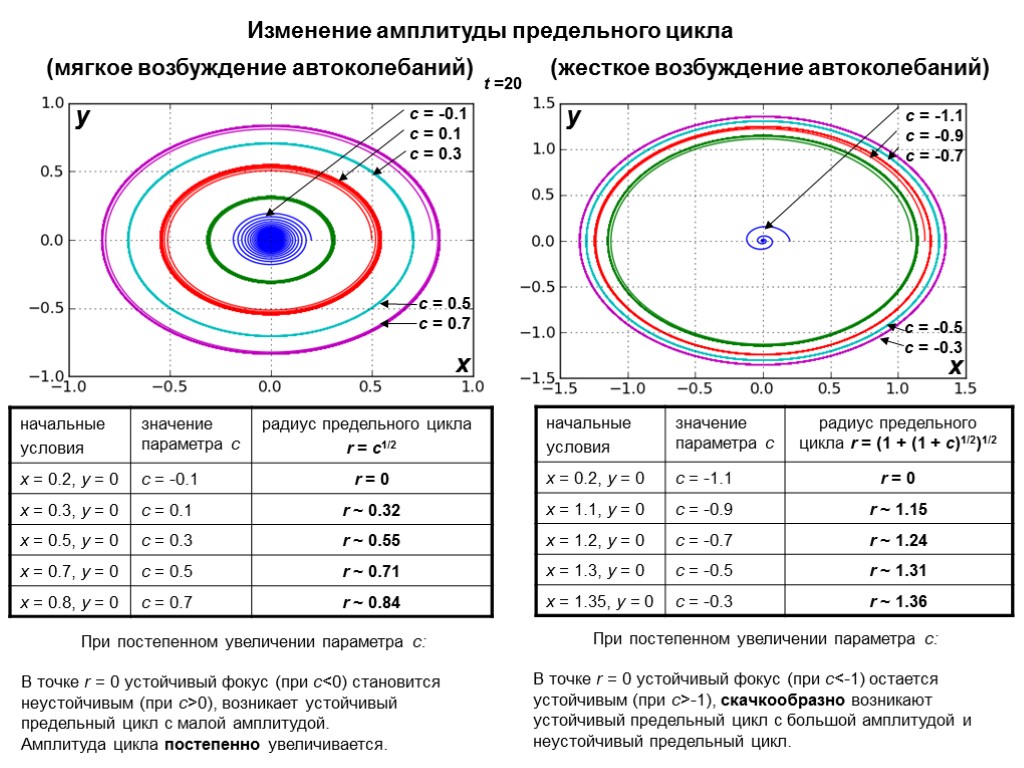>с = -0.1 с = 0.1 с = 0.3 с = 0.5 с = с = -0.1 с = 0.1 с = 0.3 с = 0.5 с = 0.7 (мягкое возбуждение автоколебаний) y x с = -1.1 с = -0.9 с = -0.7 с = -0.5 с = -0.3 (жесткое возбуждение автоколебаний) y x t =20 При постепенном увеличении параметра с: В точке r = 0 устойчивый фокус (при с<0) становится неустойчивым (при с>0), возникает устойчивый предельный цикл с малой амплитудой. Амплитуда цикла постепенно увеличивается. При постепенном увеличении параметра с: В точке r = 0 устойчивый фокус (при с<-1) остается устойчивым (при с>-1), скачкообразно возникают устойчивый предельный цикл с большой амплитудой и неустойчивый предельный цикл. Изменение амплитуды предельного цикла

>x y x y x y x y

>x y x y x y x y

>

>

>

>

>