X Workshop in Quantitative Finance January 28

X Workshop in Quantitative Finance – January 28 th, 2009 Pillar II, Concentration Risk and Financial Crisis: Remarks, Proposals, Practical issues Michele Bonollo michele. bonollo@sgsbp. it UNIVERSITA’ DEGLI STUDI DI PADOVA

The ideas in this presentation arise from a theoretical work with F. Mercurio and P. Mosconi “Basel II Second Pillar: an Analytical Va. R with Contagion and Sectorial Risks” And from a more applied work with M. Pegorin and P. Mosconi “Il rischio di concentrazione nel II pilastro Semplice Add. On o modello di Portafoglio? Proposte e Applicazioni” (submitted to Bancaria) The aim of these slides is to show also a “simple” concept such as concentration requires a deep work to be managed and embedded in any model; finally, a model for several levels of concentration is shown.

Remark 1: What to learn form crisis? In a very genereral perspective, across different types of risk (credit, counterparty, liquidiy, market, . . ) some things have to be better understood from both practioners and academic researchers: • The true problem is not the mathematicl model, both the parameters, such as PD / ratings, correlations, and the operational data (deals, instruments, …) • Sometimes the rare event happen (Lehman, …) • Is the market view always the right view? • CDS spread vs. rating & default frequency • Very high implied volatility • … • Risk management is not only methodology, but (mainly) • To have a process, with different levels of ownership • To have a senior strategic view of business, e. g. the close relationship OTC portfolios and counterpary risk

Remark 2: What is Pillar II ? Roughly speaking, Pillar II is that part of Basle II framework (Circ. 263 for Italy), that concerns: The measure of other types of risk, such as liquidity risk, business risk, … • The measure of the Add-ON for concentration risk in credit risk • The integrated measure of the global risk (market, credit, …) • The set up on an internal control process in order to verify the adequacy of the capital itself; this process is well known as ICAAP, and requires also to make stress tests A “proportionality principle” is allowed, that is the small bank may use simpler or standard models. The final purpose is that the bank must be more efficient in measuring their risks and allocating the capital •

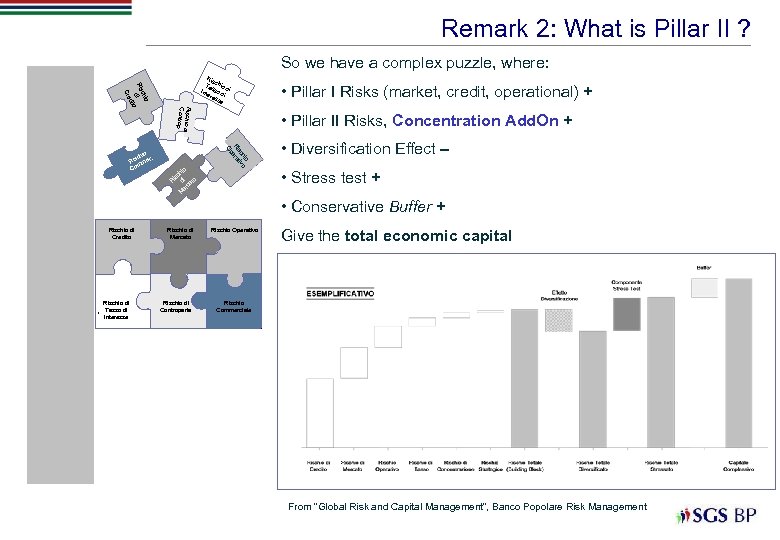Remark 2: What is Pillar II ? So we have a complex puzzle, where: Rischio di Controp. o chi Ris di dito Cre Ris c Ta hio d Int sso d i ere i sse o hi sc i o d at c er M • Pillar II Risks, Concentration Add. On + o hi o sc tiv Ri era Op io ch. Ris mer m Co • Pillar I Risks (market, credit, operational) + • Diversification Effect – • Stress test + Ri • Conservative Buffer + Rischio di Credito Rischio di Tasso di Interesse Rischio di Mercato Rischio di Controparte Rischio Operativo Give the total economic capital Rischio Commerciale From “Global Risk and Capital Management”, Banco Popolare Risk Management

Remark 3: Why Concentration Add-On for Credit? In the Pillar I approach, the internal models for the different risk consist of: • a Va. R approach for Market risk (99%, 10 days) • a Va. R approach for Operational Risk (99% for the different business lines) • a quasi Va. R approach for the Credit capital requirement, in the sense that it is a 99. 9% Va. R under some strict hypothesis, mainly: • a Merton/Credit metrics model (defaul when the asst retursn is under a level) • perfect granularity of the different positions • only one systematic backgrounf factor (the “Economy”) This is why the regulator has embedded in the Pillar II a surcharge of capital, the so called Add. On

Remark 4: What Concentration is ? In the graduate courses, the concentration is one of the measures that are studies in the “descriptive statistics” context. It is related to the distribution of some physical quantity or amount along the sample/population. A classical indicator is the Gini index, another one is the Shannon entropy indicator, finally the Herfindahl index H, that comes from the market trust studies. Let Ei be the values, i = 1…N, wi the normalized weights, wi = Ei / SEi, then H = S i w i 2

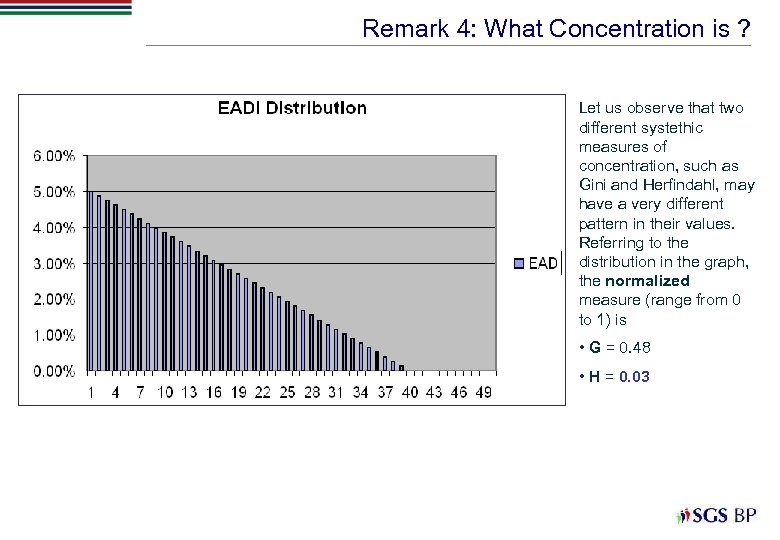Remark 4: What Concentration is ? Let us observe that two different systethic measures of concentration, such as Gini and Herfindahl, may have a very different pattern in their values. Referring to the distribution in the graph, the normalized measure (range from 0 to 1) is • G = 0. 48 • H = 0. 03

Remark 5: Add-ON or risk decomposition? In the Bank of Italy circ. 263 we find “Concentration risk: the risk coming from expositions to counterparties, groups of linked counterparties, counterparties of the same economic or geographic cluster, …” Single name Add. On Contagion Effect Sector Effect In an implicit (? ) way, the add-on requirement is a bridge to credit portfolio models, especially to some analytical approach or approximation, in order to get risk decomposition, i. e. Va. RPillar. I + Add. ON = Va. RPillar. I + (Single Name + Sector + Contagion)

Remark 6: Granularity Add. On w. r. t what Benchmark ? In the Basle II, one may find an explicit example to explain the meaning of granularity (annex B, Title 3, Circ. 263 Bank of Italy): Briefly, the regulator refers to the EAD (exposure at default) key variable and to the fact that the Pillar one formula unfortunately gives the same output for the credit risk, for concentrated or well distributed set of exposures.

Proposal 1: Short Review -Gordy (1998, 2000, …): Credit Risk+ (binomial) framework, single factor, single name add on - Emmer-Tasche (2003, . . ): credit Metrics Framewok, single name add on - Pyntchin (2004), Single nam and sector add on - Basle II : the suggested add on is based on Gordy and Tasche studies, on the fact that, the II order taylor expansion of Va. R is linear in the Herfindahl index, through a b that must be calibrated depending on the set of paramaters (PD, LGD, r),

Proposal 2: Notation

Proposal 3: Specification The asset return is a standard normal Xi ri is the sensitivity to the systematic risk; the Yi is a composite factor that can be expressed as It turn out that we can rearrange Yi and get

Proposal 4: Specification The representation can be analyzed as follows:

Proposal 5: Contagion Generally speaking, contagion is a link between two companies, due to some possibles reasons, such as supplier-purchaser interaction and so on. Here we propose a simlified but not too irrealistic approach: companies belong to two classes: the companies immune to contagion, the I-class (I = Infecting) and the C-class, which have an actual contagion risk. For the C-class, the asset return is given by

Proposal 6: Contagion

Proposal 7: Va. R Decomposition and results We define the portfolio credit loss L as usual by The goal is to compute the quantile of the loss for a given confidence level q, let tq(L). Let L the limiting loss distribution in the one-factor Merton Model. We have

Proposal 8: Va. R Decomposition and results By Taylor expansion , first term order vanish and we get The term n(y) is the conditional variance = var(L | Y = y), we can decompose it again

Proposal 9: Va. R Decomposition with contagion The previous result is similar to Pyntchin. The new proposal is for contagion where the decomposition becomes appealing

Proposal 10: Numerical Applications

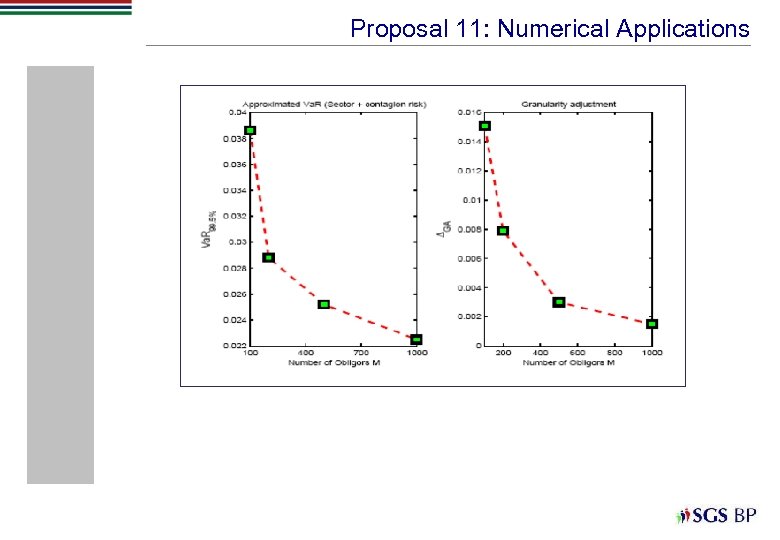Proposal 11: Numerical Applications

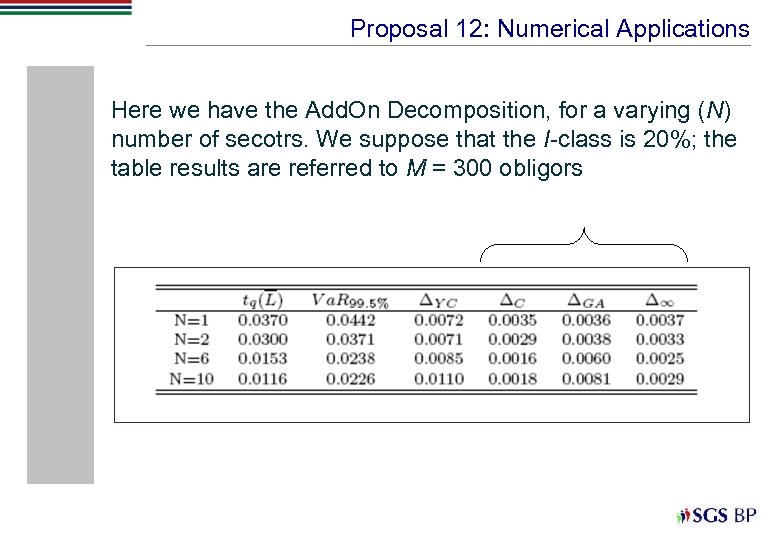Proposal 12: Numerical Applications Here we have the Add. On Decomposition, for a varying (N) number of secotrs. We suppose that the I-class is 20%; the table results are referred to M = 300 obligors

Practical Issues 1: The actual goal To make software for risk management is different from buildinf models. We point out that in this situation one has to emphasize: • the robustness (reliability) of the process: each day I want to have an output; if not, to know why • computational performances: in credit risk, medium bank have more than one millions of positions and 100 k borrowers • an efficient management of mkissing data and poor quality data

Practical Issues 2: The actual data flow Operational data Mapping Data Risk_Parameters • Borrower_Id • Borrower_cluster • PD • Loan_Id • Borrower_profession • LGD • Net_Amount • Product_LGD • sector correlation • Product_ID • Borrower_rating • factor loading • . , . . . • …. These data are always available in the Bank DB, but sometimes they are missing, or poor quality, or filled “by default” Here we have the most difficult problems: how to estimate the data? How may cluster sectors? Make vs. Buy for correlations? How to assess the factor loadings? …

Some conclusions • The concentration is still an open issue for both theoretical and applied research: • Our proposal enhances for contagion effects some previous approaches • But …the hard challenge is to run it (as every model) inside an actual risk managament process • risk measure and decomposition • limits control • to take decisions