X Теория вероятности с элементами математической статистики В

X Теория вероятности с элементами математической статистики В начало Назад Далее

X Случайное событие Ø подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности. В начало Назад Далее

X Ø Случайное событие, которое никогда не реализуется в результате случайного эксперимента, называется невозможным и обозначается символом Ø Случайное событие, которое всегда реализуется в результате случайного эксперимента, называется достоверным и обозначается символом Ω. В начало Назад Далее

X Несколько событий называются несовместимыми Ø если никакие два из них не могут появиться одновременно в результате однократного испытания случайного эксперимента. В начало Назад Далее

Вероя тность (вероятностная мера) X Ø численная мера степени объективной возможности наступления случайного события. Оценкой вероятности события может служить частота его наступления в длительной серии независимых повторений случайного эксперимента. В начало Назад Далее

X Теория вероятностей Ø раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними. В начало Назад Далее

X Ø Пусть производится некоторое испытание, которое имеет n различных несовместных и равновозможных исходов. Ø Вероятность события A, которое может появиться в результате этого испытания, называют число где m – число исходов испытания, благоприятствующих событию A. В начало Назад Далее

Анализ решения задач 1. Выясните, в чем состоит испытание, рассматриваемое в задаче. 2. Установите, являются ли исходы испытания несовместными и равновозможными. 3. Подсчитайте число всех возможных исходов испытания (n). 4. Сформулируйте событие А, вероятность наступления которого требуется найти. 5. Подсчитайте число исходов испытания благоприятствующих событию А. 6. По формуле высчитайте вероятность события А. В начало Назад Далее X

X Сложение и умножение вероятностей Ø Пусть с некоторым испытанием связаны события А и В. Их суммой называется событие А+В, состоящее в появлении события А или события В, или обоих этих событий. Ø Произведением событий А и В называется событие АВ, состоящее в совместном появлении тих событий. В начало Назад Далее

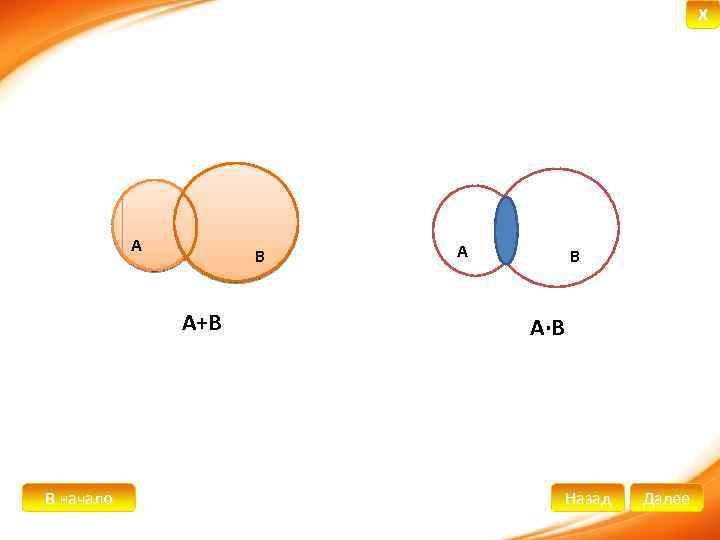X А В А+В В начало А В А∙В Назад Далее

X Правило суммы Если объект А может быть выбран m способами, а объект В – другими n способами, причем выбор объектов А и В несовместны, то выбор «А или В» можно сделать m+n способами. В начало Назад Далее

Правило произведения Если объект А может быть выбран m способами и после каждого из этих выборов В может быть выбран n способами, то выбор упорядоченной пары (А, В) можно сделать m·n способами. В начало Назад Далее X

X Перестановки Ø это комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Ø Число всех возможных перестановок их n элементов равно: Pn=n!, где n!=1∙ 2 ∙ 3…n, 0!=1 В начало Назад Далее

X Перестановки с повторением Ø Если среди n элементов есть n 1 элементов одного вида, n 2 элементов другого вида и т. д. , то число перестановок равно: В начало Назад Далее

X Размещения Ø это комбинации, составленные из n различных элементов по k элементов, которые обличаются либо составом элементов, либо их порядком. Ø Число всех возможных размещений их n элементов равно: В начало Назад Далее

X Размещение с повторением В начало Назад Далее

X Сочетание Ø это комбинации, состоящие из n различных элементов по k элементов, которые отличаются только составом элементов. Ø Число сочетаний из n элементов по k элементов. В начало Назад Далее

X Сочетание с повторениями В начало Назад Далее