Корень, степень, логарифмы.ppt
- Количество слайдов: 40
 X Лекция № 2 КОРЕНЬ, СТЕПНЬ, ЛОГАРИФМЫ…. . преподаватель математики Маслова Татьяна Федоровна В начало Назад Далее
X Лекция № 2 КОРЕНЬ, СТЕПНЬ, ЛОГАРИФМЫ…. . преподаватель математики Маслова Татьяна Федоровна В начало Назад Далее
 X Степень с рациональным показателем В начало Действия со степенями Назад Далее
X Степень с рациональным показателем В начало Действия со степенями Назад Далее
 X Корень n й степени Любое решение уравнения где n = 2, 3, … называется корнем n – й степени из числа b. В начало Назад Далее
X Корень n й степени Любое решение уравнения где n = 2, 3, … называется корнем n – й степени из числа b. В начало Назад Далее
 X Арифметический корень n й степени Неотрицательное решение уравнения n = 2, 3, … называется арифметическим корнем n – й степени из числа b. В начало Назад Далее
X Арифметический корень n й степени Неотрицательное решение уравнения n = 2, 3, … называется арифметическим корнем n – й степени из числа b. В начало Назад Далее
 X Обозначение арифметического корня При n = 2 арифметический корень из числа b обозначается При n = 3, 4, … арифметический корень из числа b обозначается В начало Назад Далее
X Обозначение арифметического корня При n = 2 арифметический корень из числа b обозначается При n = 3, 4, … арифметический корень из числа b обозначается В начало Назад Далее
 X Пример 1: Какое из равенств верно? Решение: В начало Назад Далее
X Пример 1: Какое из равенств верно? Решение: В начало Назад Далее
 X Пример 2: Какое из равенств неверно? Решение: Запись ошибочна, т. к. символ используется только для В начало Назад Далее
X Пример 2: Какое из равенств неверно? Решение: Запись ошибочна, т. к. символ используется только для В начало Назад Далее
 X Пример 3: Решить уравнение: Решение: Запись Замечание: Обозначение В начало является неверным Назад Далее
X Пример 3: Решить уравнение: Решение: Запись Замечание: Обозначение В начало является неверным Назад Далее
 Степень с рациональным показателем В начало Назад Далее X
Степень с рациональным показателем В начало Назад Далее X
 Запрещенные операции: В начало Назад Далее X
Запрещенные операции: В начало Назад Далее X
 X Модуль (абсолютная величина) числа В начало Назад Далее
X Модуль (абсолютная величина) числа В начало Назад Далее
 X Сравнение степеней с одним основанием В начало Назад Далее
X Сравнение степеней с одним основанием В начало Назад Далее
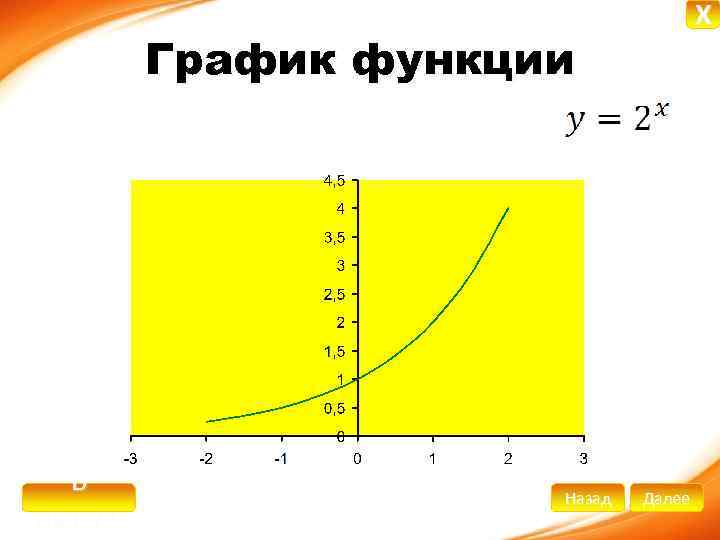 X График функции В начало Назад Далее
X График функции В начало Назад Далее
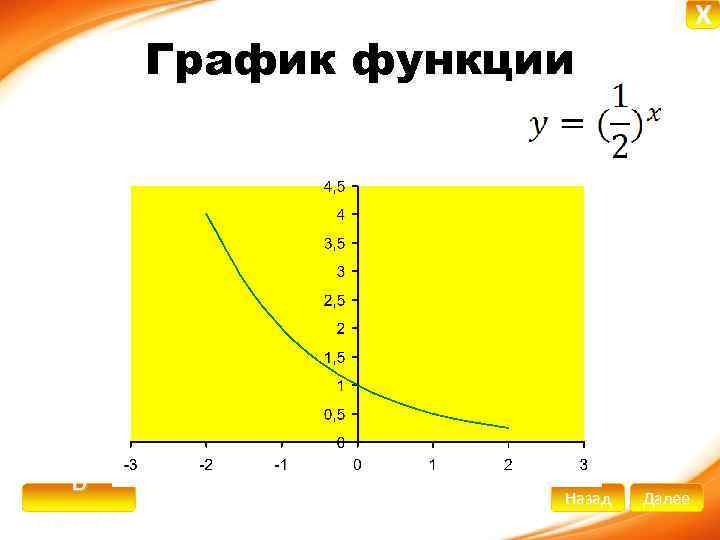 X График функции В начало Назад Далее
X График функции В начало Назад Далее
 X Примеры: 1. Найдем значение выражения 2. Найдем значение выражения 3. Найдем значение выражения В начало Назад Далее
X Примеры: 1. Найдем значение выражения 2. Найдем значение выражения 3. Найдем значение выражения В начало Назад Далее
 X Примеры: 1. Упростим выражение: 2. Упростим выражение: В начало Назад Далее
X Примеры: 1. Упростим выражение: 2. Упростим выражение: В начало Назад Далее
 X Примеры: 1. Упростим выражение: 2. Упростим выражение: 3. В начало Упростим выражение: Назад Далее
X Примеры: 1. Упростим выражение: 2. Упростим выражение: 3. В начало Упростим выражение: Назад Далее
 X Примеры: 1. Упростим выражение: 2. Упростим выражение: В начало Назад Далее
X Примеры: 1. Упростим выражение: 2. Упростим выражение: В начало Назад Далее
 X Степени В начало Назад Далее
X Степени В начало Назад Далее
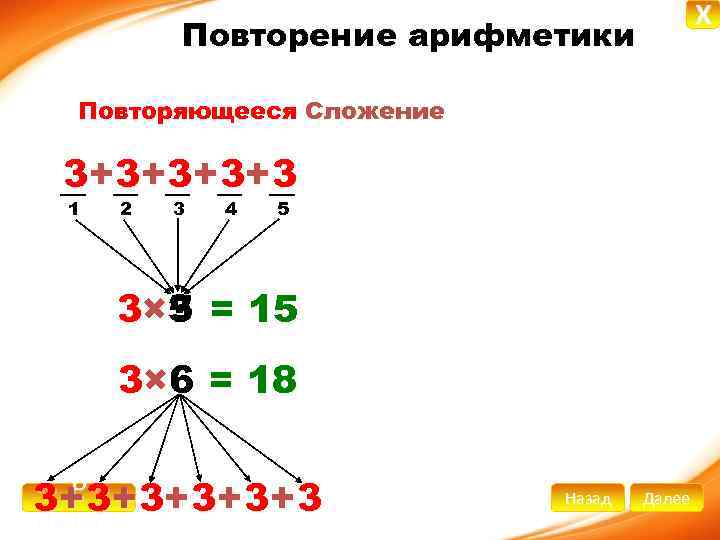 X Повторение арифметики Повторяющееся Сложение 3 + 3+ 3+ 3 1 2 3 4 5 ? 3× 5 = 15 3× 6 = 18 В 3+ 3+ 3+ 3 начало Назад Далее
X Повторение арифметики Повторяющееся Сложение 3 + 3+ 3+ 3 1 2 3 4 5 ? 3× 5 = 15 3× 6 = 18 В 3+ 3+ 3+ 3 начало Назад Далее
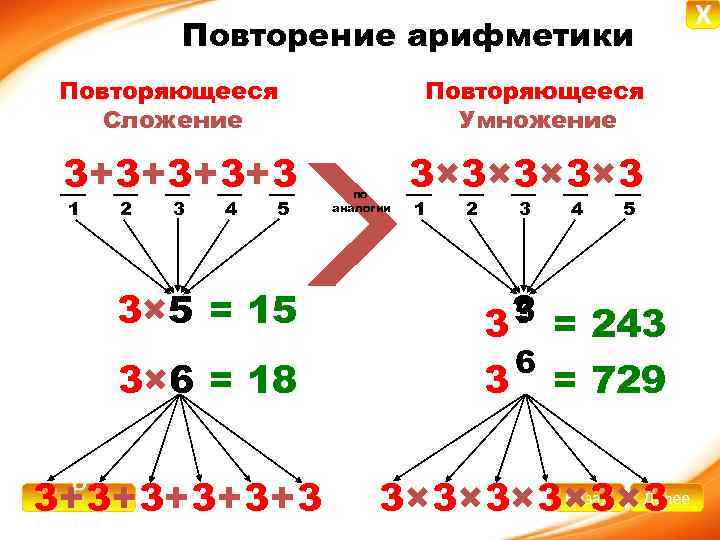 Повторение арифметики Повторяющееся Сложение 3 + 3+ 3+ 3 1 2 3 4 5 3× 5 = 15 3× 6 = 18 В 3+ 3+ 3+ 3 начало Повторяющееся Умножение по аналогии 3 × 3× 3× 3 1 2 3 4 5 5 ? = 243 3 6 3 = 729 Назад Далее 3× 3× 3× 3 X
Повторение арифметики Повторяющееся Сложение 3 + 3+ 3+ 3 1 2 3 4 5 3× 5 = 15 3× 6 = 18 В 3+ 3+ 3+ 3 начало Повторяющееся Умножение по аналогии 3 × 3× 3× 3 1 2 3 4 5 5 ? = 243 3 6 3 = 729 Назад Далее 3× 3× 3× 3 X
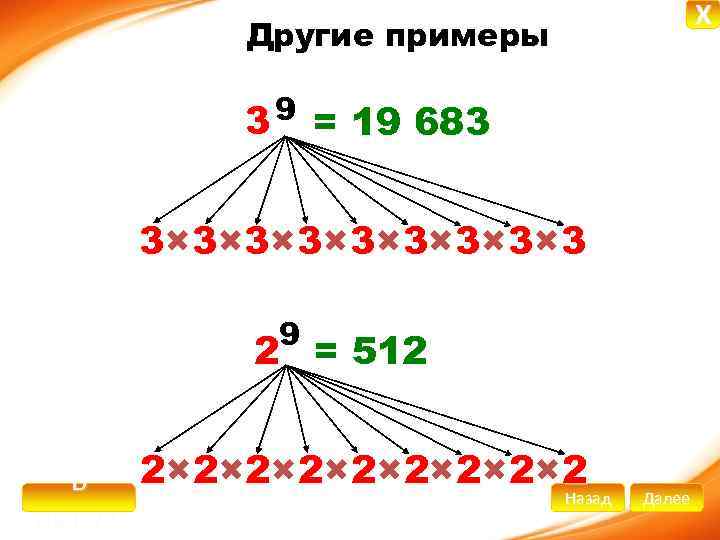 X Другие примеры 9 = 19 683 3 3× 3× 3 9 2 = 512 В начало 2× 2× 2 Назад Далее
X Другие примеры 9 = 19 683 3 3× 3× 3 9 2 = 512 В начало 2× 2× 2 Назад Далее
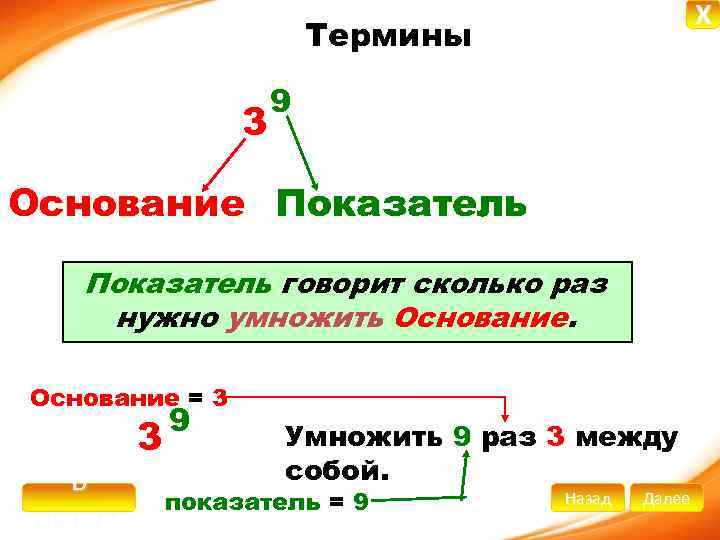 X Термины 3 9 Основание Показатель говорит сколько раз нужно умножить Основание = 3 В начало 3 9 Умножить 9 раз 3 между собой. показатель = 9 Назад Далее
X Термины 3 9 Основание Показатель говорит сколько раз нужно умножить Основание = 3 В начало 3 9 Умножить 9 раз 3 между собой. показатель = 9 Назад Далее
 X Попрактикуемся… 32 =9 53 = 125 04 = 0 34 = 81 73 = 343 43 103 = 1 000 151 = 15 26 = 64 19 =1 = 64 В начало Назад Далее
X Попрактикуемся… 32 =9 53 = 125 04 = 0 34 = 81 73 = 343 43 103 = 1 000 151 = 15 26 = 64 19 =1 = 64 В начало Назад Далее
 Найти показатель степени 1 2 3 4 5 6 показатель 6 5× 5× 5× 5 = 5__ основание 4 8× 8× 8× 8 = 8__ 7 2× 2× 2× 2 = 2__ 2 7× 7 = 7__ 5 1. 5× 1. 5 = 1. 5__ 11 4× 4× 4× 4 = 4__ В начало Назад Далее X
Найти показатель степени 1 2 3 4 5 6 показатель 6 5× 5× 5× 5 = 5__ основание 4 8× 8× 8× 8 = 8__ 7 2× 2× 2× 2 = 2__ 2 7× 7 = 7__ 5 1. 5× 1. 5 = 1. 5__ 11 4× 4× 4× 4 = 4__ В начало Назад Далее X
 X Как читать степень 39 4 5 2 7 3 10 В начало “Три в девятой степени” “Пять в четвертой степени” “Семь во второй степени” “или Семь в квадрате” квадрате “Десять в третьей степени” “или Десять в кубе” кубе Назад Далее
X Как читать степень 39 4 5 2 7 3 10 В начало “Три в девятой степени” “Пять в четвертой степени” “Семь во второй степени” “или Семь в квадрате” квадрате “Десять в третьей степени” “или Десять в кубе” кубе Назад Далее
 X Попрактикуемся … 2 5 = 25 4 0 =0 3 0 =0 x 9 = 729 4 4 = 256 2 17 = 289 14 1 =1 1 3 =3 4 7 = 2 401 В начало Назад Далее
X Попрактикуемся … 2 5 = 25 4 0 =0 3 0 =0 x 9 = 729 4 4 = 256 2 17 = 289 14 1 =1 1 3 =3 4 7 = 2 401 В начало Назад Далее
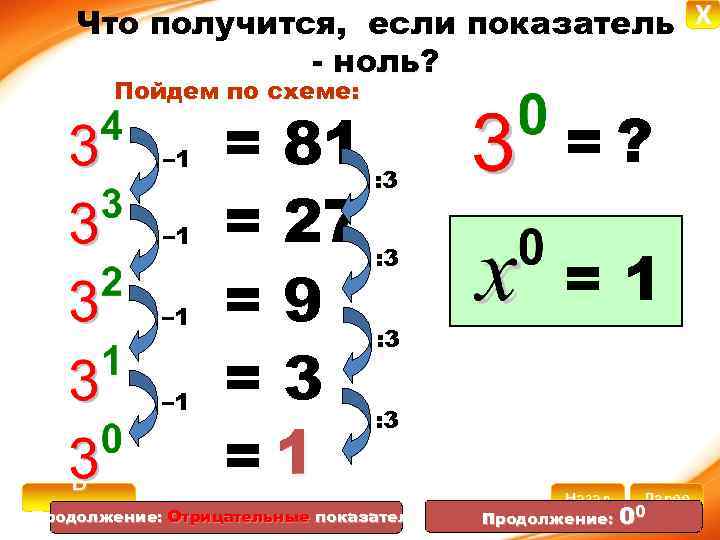 Что получится, если показатель X - ноль? Пойдем по схеме: – 1 – 1 = 81 = 27 =9 =3 =1 : 3 =? =1 : 3 В Продолжение: Отрицательные показатели начало Назад Далее Продолжение: 00
Что получится, если показатель X - ноль? Пойдем по схеме: – 1 – 1 = 81 = 27 =9 =3 =1 : 3 =? =1 : 3 В Продолжение: Отрицательные показатели начало Назад Далее Продолжение: 00
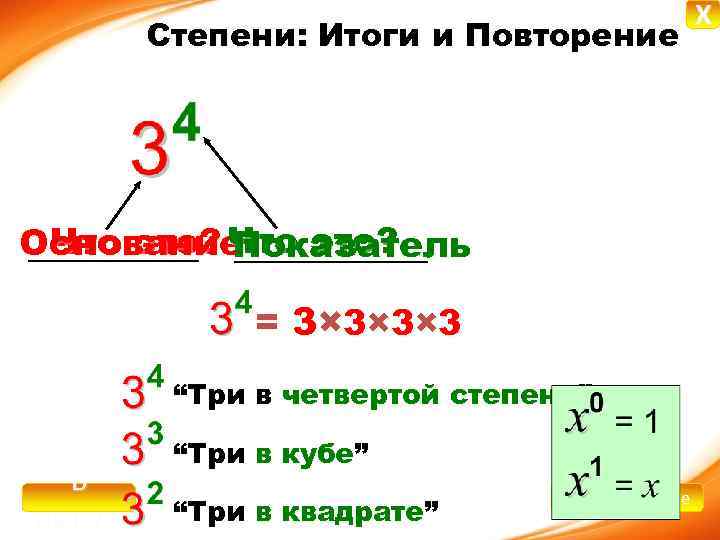 Степени: Итоги и Повторение Что это? Основание Показатель = 3 × 3 × 3 “Три в четвертой степени” степени В начало “Три в кубе” кубе “Три в квадрате” квадрате Назад Далее X
Степени: Итоги и Повторение Что это? Основание Показатель = 3 × 3 × 3 “Три в четвертой степени” степени В начало “Три в кубе” кубе “Три в квадрате” квадрате Назад Далее X
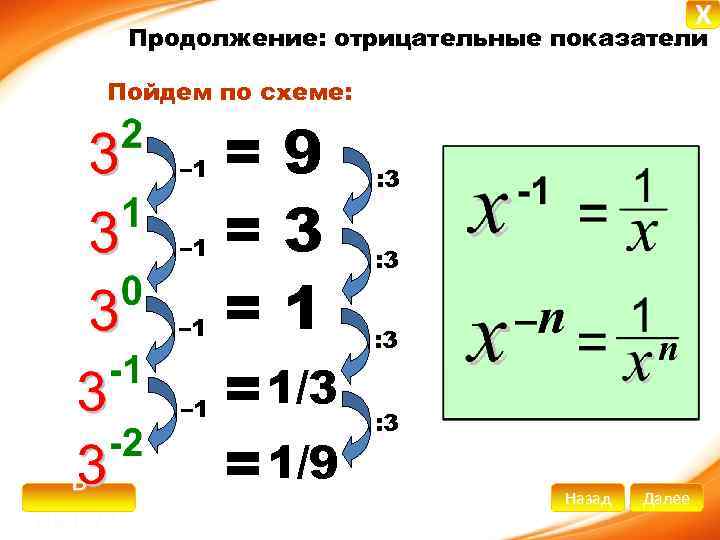 X Продолжение: отрицательные показатели Пойдем по схеме: – 1 – 1 В начало =9 =3 =1 = 1/3 = 1/9 : 3 : 3 Назад Далее
X Продолжение: отрицательные показатели Пойдем по схеме: – 1 – 1 В начало =9 =3 =1 = 1/3 = 1/9 : 3 : 3 Назад Далее
 Попрактикуемся… X – 4 1 =1 – 12 1 =1 2 – 1 = 1/2 – 2 = 1/16 – 3 = 1/27 – 3 = Назад Далее 1/1000 4 3 В начало 10
Попрактикуемся… X – 4 1 =1 – 12 1 =1 2 – 1 = 1/2 – 2 = 1/16 – 3 = 1/27 – 3 = Назад Далее 1/1000 4 3 В начало 10
 X Продолжение: Ноль в Нулевой Степени? 0 0 ? Что это означает? 0 x =1 Правило 1: Правило 2: x 0 =0 Любое число в степени 0 = 1. Ноль в любой степени = 0 Какое правило нужно применить? В начало Назад Далее
X Продолжение: Ноль в Нулевой Степени? 0 0 ? Что это означает? 0 x =1 Правило 1: Правило 2: x 0 =0 Любое число в степени 0 = 1. Ноль в любой степени = 0 Какое правило нужно применить? В начало Назад Далее
 X Логарифм числа В начало Назад Далее
X Логарифм числа В начало Назад Далее
 X Логарифмом числа b, по основанию а, где b>0, a>0, а≠ 1, называется показатель степени, в которую надо возвести а, чтобы получить число b. В начало Назад Далее
X Логарифмом числа b, по основанию а, где b>0, a>0, а≠ 1, называется показатель степени, в которую надо возвести а, чтобы получить число b. В начало Назад Далее
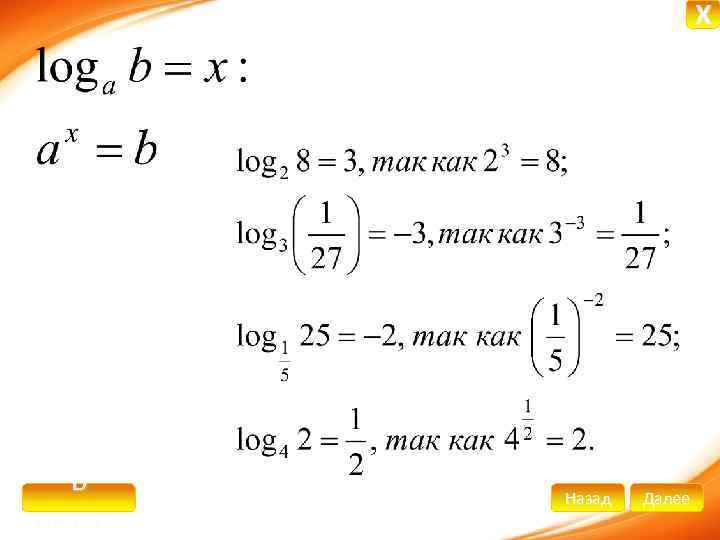 X В начало Назад Далее
X В начало Назад Далее
 Из определения логарифма следует: Основное логарифмическое тождество В начало Назад Далее X
Из определения логарифма следует: Основное логарифмическое тождество В начало Назад Далее X
 Из определения следует: В начало Назад Далее X
Из определения следует: В начало Назад Далее X
 X для любого действительного В начало Назад p Далее
X для любого действительного В начало Назад p Далее
 X Взаимно обратные действия: Возведение в степень В начало Логарифмирование Назад Далее
X Взаимно обратные действия: Возведение в степень В начало Логарифмирование Назад Далее
 X v. Решить уравнение: v. При каких х существует ? + В начало 1 + 2 Назад х Далее
X v. Решить уравнение: v. При каких х существует ? + В начало 1 + 2 Назад х Далее


