X Лекция 14 Степенные и показательные функции

X Лекция № 14 Степенные и показательные функции преподаватель математики Маслова Татьяна Федоровна В начало Назад Далее

X Степенна я фу нкция Ø функция y = xa, где a (показатель степени) — некоторое вещественное число. В начало Назад Далее

X Ø К степенным часто относят и функцию вида y = kxa, где k — некоторый масштабный множитель. Ø Существует также комплексное обобщение степенной функции. На практике показатель степени почти всегда является целым или рациональным числом. В начало Назад Далее

X Область определения Если показатель степени — целое число, то можно рассматривать степенную функцию на всей числовой прямой (кроме, возможно, нуля). В общем случае степенная функция определена при x > 0. Если a > 0, то функция определена также и при x = 0, иначе нуль является её особой точкой. В начало Назад Далее

Рациональный показатель степени Ø Графики степенной функции при натуральном показателе n называются параболами порядка n. При a = 1 получается функция y = kx, называемая прямой пропорциональной зависимостью. Ø Графики функций вида y = x − n, где n — натуральное число, называются гиперболами порядка n. При a = − 1 получается функция y=k/x, называемая обратной пропорциональной зависимостью. Ø Если a=1/n, то функция есть арифметический корень степени n. В начало Назад Далее X

Показательная функция Ø математическая функция f(x)=ax. В начало Назад Далее X

X Ø В вещественном случае основание степени — некоторое неотрицательное вещественное (действительное) число, а аргументом функции является вещественный показатель степени. Ø В теории комплексных функций рассматривается более общий случай, когда аргументом и показателем степени может быть произвольное комплексное число. Ø В самом общем виде — uv, введена Лейбницем в 1695 г. В начало Назад Далее

X Особо выделяется случай, когда в качестве основания степени выступает число e. Такая функция называется экспонентой (вещественной или комплексной). В начало Назад Далее

Определение показательной функции Пусть a — неотрицательное вещественное число, x — рациональное число: x=m/n. Тогда ax определяется по следующим правилам. Ø Если x > 0, то Ø Если x = 0, то Ø Если x < 0, то (для a > 0) В начало Назад Далее X

К основным свойствам показательной функции y = ax при a > 1 относятся: Ø Область определения функции − вся числовая прямая. Ø Область значений функции − промежуток (0; +∞) Ø Функция строго монотонно возрастает на всей числовой прямой, то есть, если x 1

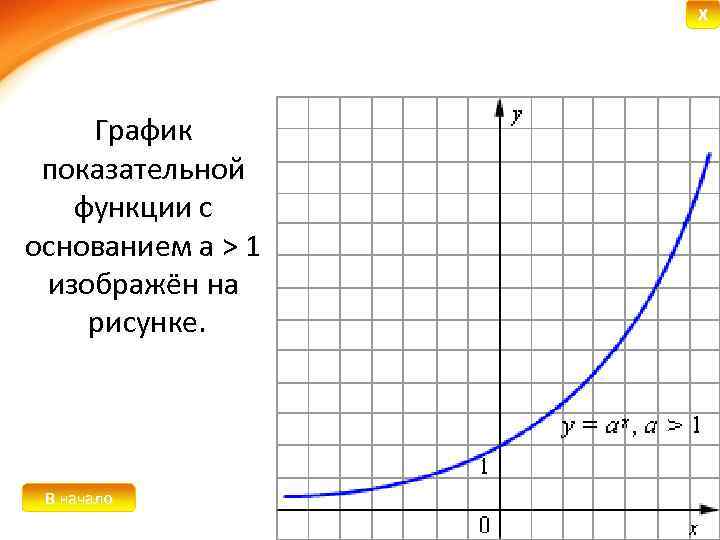X График показательной функции с основанием a > 1 изображён на рисунке. В начало Назад Далее

К основным свойствам показательной функции y = ax при 0 < a < 1 относятся: Ø Область определения функции − вся числовая прямая. Ø Область значений функции − промежуток (0; +∞) Ø Функция строго монотонно убывает на всей числовой прямой, то есть , если x 1

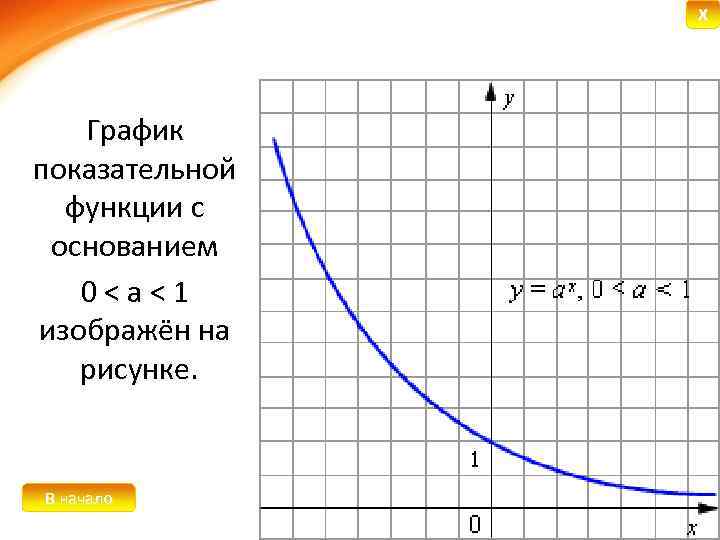X График показательной функции с основанием 0

X Пример Ø Упростите выражение В начало Назад Далее

X Пример Ø Решите уравнение: Ø Приведём уравнение к виду Ø Имеем Ø Отсюда получается В начало Назад Далее