Wrapping up Section 1 3 Section 1 4

Wrapping up Section 1. 3 Section 1. 4 Implication/Conditionals Biconditionals Logical Equivalence

Conditional/Implication • In logic this is written in the form: p q • We state that p is the hypotheses or the antecedent (or assumption or premise) • We state that q is the conclusion or the consequent

In-Class Activity #1 Identify the hypothesis/antecedent in each of the following implication statements • If you study in this course you will get an A. • Tomorrow is Friday if today is Thanksgiving. • n is prime implies n is odd or n is 2. • Tim is Ann’s father is sufficient for Jim being her uncle and Sue being her aunt. • n is divisible by 6 only if n is divisible by 2 and n is divisible by 3. • P being a rectangle is necessary for P being a square.

In-Class Activity #1 • If you study in this course you will get an A. Study Get an A • Tomorrow is Friday if today is Thanksgiving. Today is Thanksgiving Tomorrow is Friday • n is prime implies n is odd or n is 2. n is prime n is odd or n is 2

In-Class Activity #1 • Tim is Ann’s father is sufficient for Jim being her uncle and Sue being her aunt. Tim is Ann’s father Jim is her uncle and Sue is her aunt • n is divisible by 6 only if n is divisible by 2 and n is divisible by 3. n is divisible by 6 n is divisible by 2 and n is divisible by 3 • P being a rectangle is necessary for P being a square. P is a square P is a rectangle

Conditional/Implication • The original statement is False when p is true and q is false; otherwise it is true. p T T F q T F T p q T F F T

Conditional/Implication • A conditional statement that is true by virtue of the hypothesis being false is called vacuously true or true by default. • (This situation always messes with students) p T T F q T F T p q T F F T

In-Class Activity #2 • Complete the following Truth Table Original p q T T T F F ¬ p ¬ q A B C D p q q p ¬ q ¬ p ¬ q ¬ p q

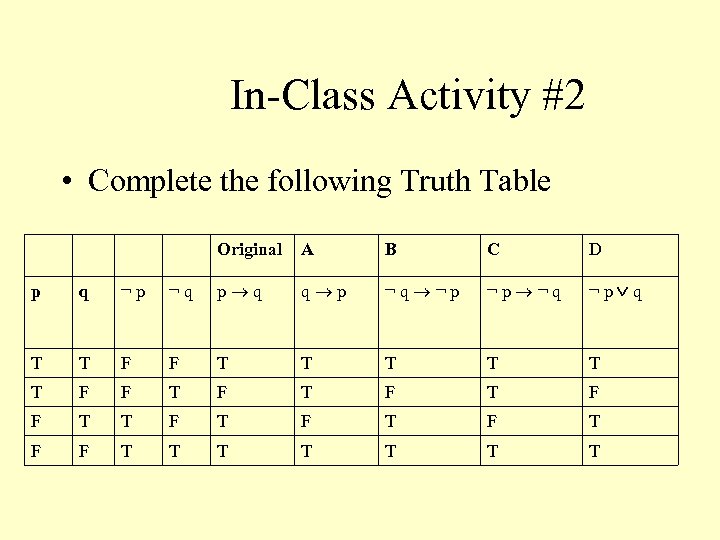In-Class Activity #2 • Complete the following Truth Table Original A B C D p q ¬ p ¬ q p q q p ¬ q ¬ p ¬ q ¬ p q T T F F T F T F T F F T T T T T

Logical Equivalence: Conditional/Implication • Notice that ( p q) ¬ p q p q T T F F T F T T ¬ p q p q T F T T

What is the negation of an implication statement • How do we write: ¬( p q) • Remember that: ( p q) ¬ p q • Therefore: ¬ ( p q) ¬ (¬ p q) ¬(¬p) ¬ q p ¬ q

Negation of an implication • ¬( p q) p ¬ q • What is the negation of “If I go to Fareway I will buy Diet Mountain Dew” • I will go to Fareway but I will NOT buy Diet Mountain Dew • Notice that this does NOT start with an if.

Contrapositive of an Implication • The contrapositive of the conditional statement “if p then q” is written as “if not q then not p” • The contrapositive of p q is written as ¬ q ¬ p

So what… • Is a conditional statement logically equivalent to it’s contrapositive? • Build the truth table and you will see that it is!

The Converse of an Implication • The converse of the conditional statement “if p then q” is written as “if q then p” • The converse of p q is written as q p

So what… • Is a conditional statement logically equivalent to it’s converse? • Build the truth table and you will see that it is not! • However, this is one of the most common logic errors made by beginning students.

The Inverse of an Implication • The inverse of the conditional statement “if p then q” is written as “if not p then not q” • The inverse of p q is written as ¬ p ¬ q

So what… • Is a conditional statement logically equivalent to it’s inverse? • Build the truth table and you will see that it is not! • HOWEVER, the converse and the inverse are logically equivalent. – One is the contrapositive of the other

In-Class Activity #3 • If my client is guilty, then the knife was in the drawer • Write the: – Converse – Contrapositive – Inverse – Negation

Converse • q p • If the knife was in the drawer then my client is guilty.

Contrapositive • ¬ q ¬ p • If the knife was not in the drawer then my client is not guilty.

Inverse • ¬ p ¬ q • If my client is not guilty than the knife is not in the drawer.

Negation • p ^ ¬ q • My client is guilty but the knife is not in the drawer. • Notice that the negation of implication is NOT an implication.

Consider • Last time I made the statement: – If I go to Fareway I will buy Diet Mountain Dew. p = “I go to Fareway” q = “I will buy DMD” • And we learned we could write this with an implication: If p then q p q

Consider • We also learned that this can be written as: – I will buy DMD if I go to Fareway. • Which is: q if p • But still written as p q

Consider • How is this statement different if instead I make the statement: – I will buy DMD only if I go to Fareway. • Notice that this is: – q only if p

Consider • I will buy DMD only if I go to Fareway. – q only if p • Notice that this is the same as saying: – If I don’t go to Fareway then I will not buy DMD ¬ p ¬ q – Whose contrapositive is: q p

So Let’s Summarize • I will buy DMD if I go to Fareway. p q • I will buy DMD only if I go to Fareway. q p • So what about: – I will buy DMD if and only if I go to Fareway: p q q p which we instead write as: p q

Biconditional • The Biconditional of p and q is written “p, if and only if, q” • It is denoted p q • It is true if both p and q have the same truth values and is false otherwise. p q T T F F F T

Biconditional • The Biconditional of p and q is written “p, if and only if, q” • It is denoted p q • It is true if both p and q have the same truth values and is false otherwise. WHY p q p q q p (p q) (q p) p q T T T F F