Wrapping up Section 1 3 Section 1 4

Wrapping up Section 1. 3 Section 1. 4 Biconditionals Logical Equivalence

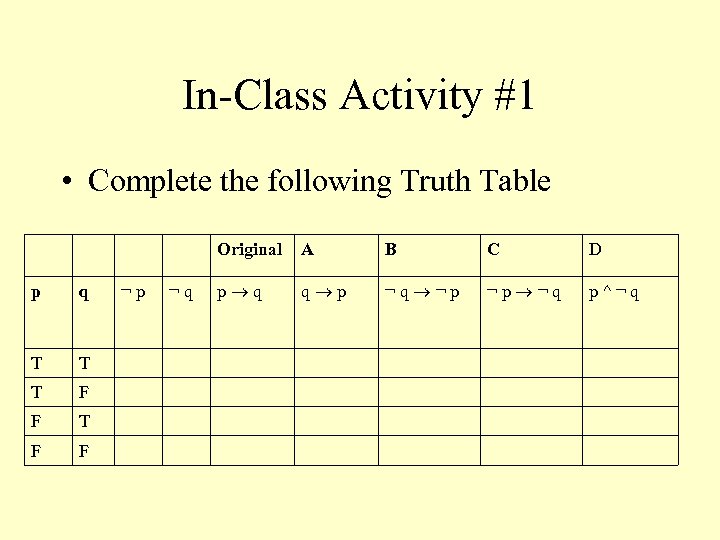In-Class Activity #1 • Complete the following Truth Table Original p q T T T F F ¬p ¬q A B C D p q q p ¬q ¬p ¬p ¬q p^¬q

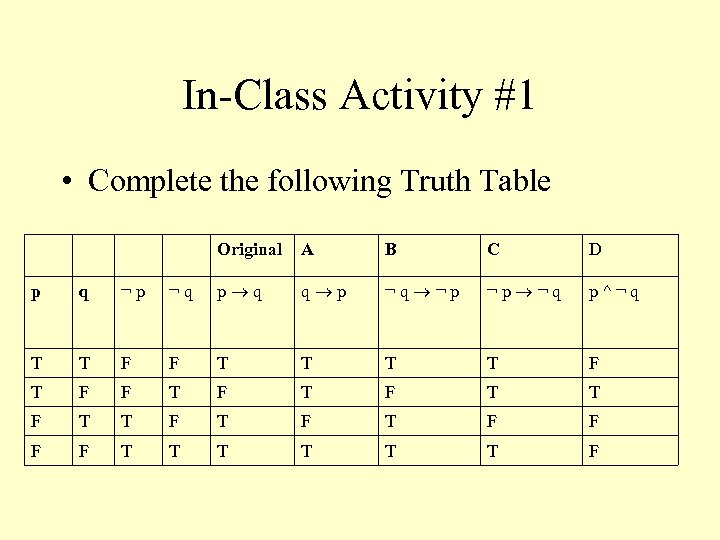In-Class Activity #1 • Complete the following Truth Table Original A B C D p q ¬p ¬q p q q p ¬q ¬p ¬p ¬q p^¬q T T F F T T F T F T F T F F T T T F

In-Class Activity #2 • Assuming that p q is the original implication, label columns A-D with their proper vocabulary names. Original A B C D p q ¬p ¬q p q q p ¬q ¬p ¬p ¬q p^¬q T T F F T T F T F T F T F F T T T F

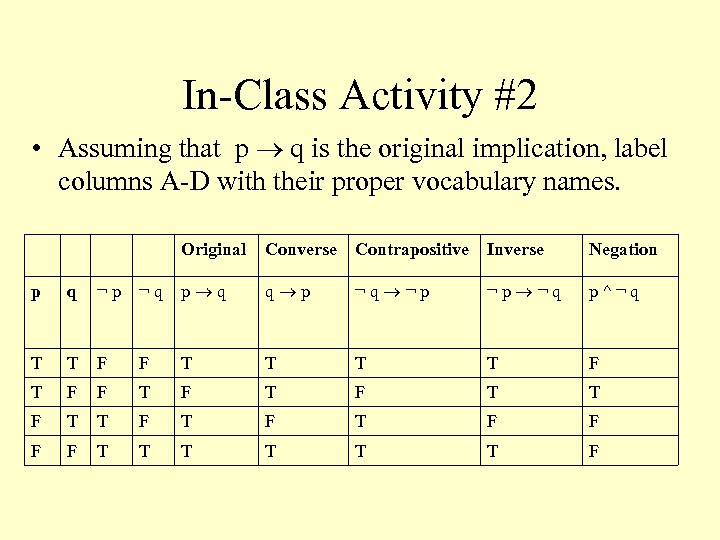In-Class Activity #2 • Assuming that p q is the original implication, label columns A-D with their proper vocabulary names. Original Converse Contrapositive Inverse Negation p q ¬p ¬q p q q p ¬q ¬p ¬p ¬q p^¬q T T F F T T F T F T F T F F T T T F

Consider • Last time I made the statement: – If I go to Fareway I will buy Diet Mountain Dew. p = “I go to Fareway” q = “I will buy DMD” • And we learned we could write this with an implication: If p then q p q

Consider • We also learned that this can be written as: – I will buy DMD if I go to Fareway. • Which is: q if p • But still written as p q

Consider • How is this statement different if instead I make the statement: – I will buy DMD only if I go to Fareway. • Notice that this is: – q only if p

Consider • I will buy DMD only if I go to Fareway. – q only if p • Notice that this is the same as saying: – If I don’t go to Fareway then I will not buy DMD ¬p ¬q – Whose contrapositive is: q p

So Let’s Summarize • I will buy DMD if I go to Fareway. p q • I will buy DMD only if I go to Fareway. q p • So what about: – I will buy DMD if and only if I go to Fareway: p q q p which we instead write as: p q

Biconditional • The Biconditional of p and q is written “p, if and only if, q” • It is denoted p q • It is true if both p and q have the same truth values and is false otherwise. p q T T F F F T

Biconditional • The Biconditional of p and q is written “p, if and only if, q” • It is denoted p q • It is true if both p and q have the same truth values and is false otherwise. WHY p q q p (p q) (q p) p q T T T F F

Vocabulary Words • Tautology • Contradiction • Logically Equivalent

In-Class Activity #3 Define these three terms • Tautology • Contradiction • Logically Equivalent

In-Class Activity #3 Define these three terms • Tautology – A compound proposition that is always true • Contradiction – A compound proposition that is never true • Logically Equivalent – Two compound propositions that result in the same truth value regardless of the truth values of their individual propositions.

Logically Equivalent • Which of the expressions from our earlier activity are logically equivalent Original Inverse Contrapositive Converse Negation p q ¬p ¬q p q q p ¬q ¬p ¬p ¬q p^¬q T T F F T T F T F T F T F F T T T F

Laws of Propositional Logic (Logically Equivalent Statements)

Using truth tables, confirm the following laws