Workshop 1 Specify a multilevel structure for

Workshop 1 • Specify a multilevel structure for EITHER a response variable of your choice OR for a model to explain house prices OR voting behaviour Template for answer • what is the response (must always be measured at level 1)? • What are the levels: 1, 2 , etc? • What are the predictor variables, and at what level are they measured (1, 2 etc)?

Varying relationships “There are NO general laws in social science that are constant over time and independent of the context in which they are embedded” Rein (quoted in King, 1976)

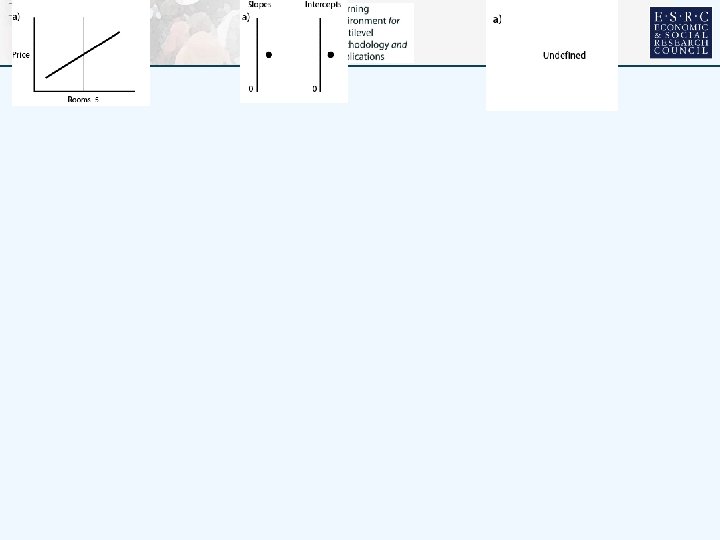
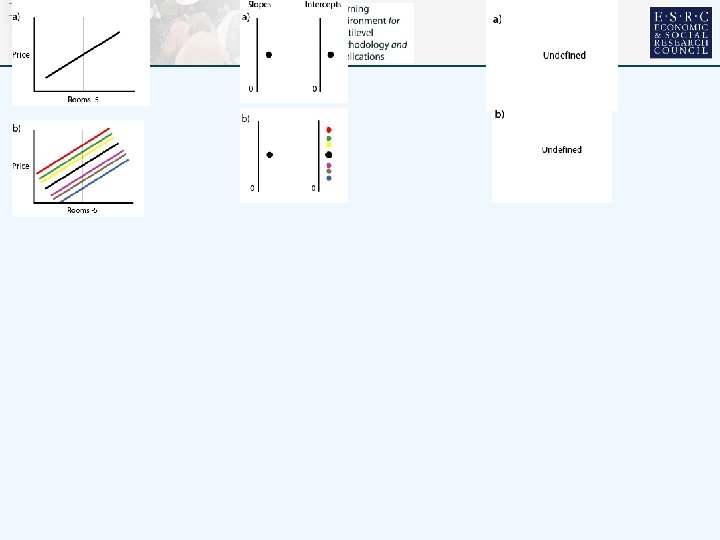
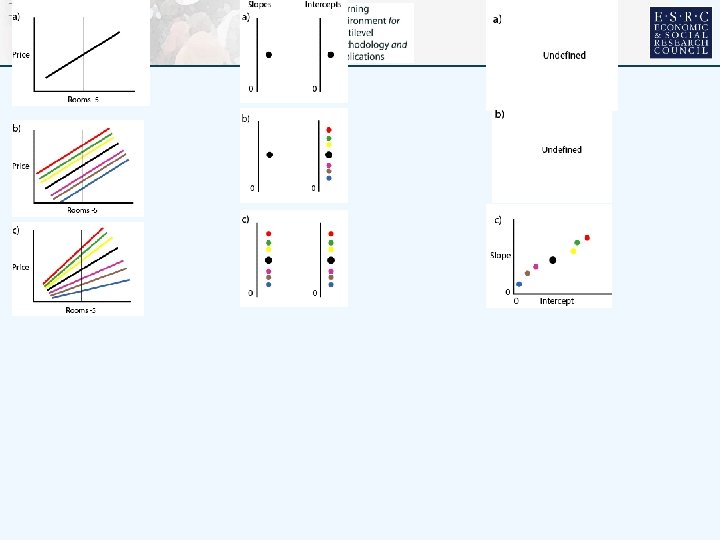
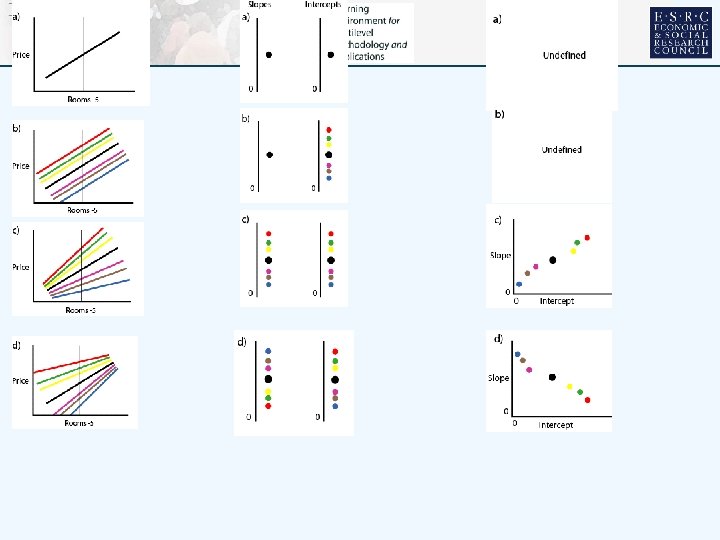
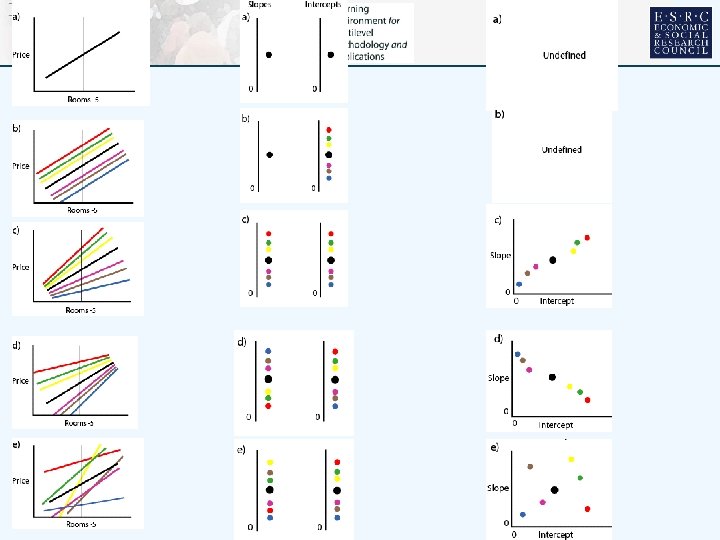
VARYING RELATIONS • • Multilevel modelling can handle multiple outcomes categorical & continuous predictors categorical and continuous responses But KISS……… Single response: house price Single predictor size of house, number of rooms Rooms • 1 -4 2 -3 3 -2 4 -1 Two level hierarchy houses at level 1 nested within neighbourhoods at level 2 are the contexts Set of characteristic plots……………… 5 0 6 1 7 2 8 3

Example of varying relations (BJPS 1992) • Stucture: 3 levels strict hierarchy individuals within constituencies within regions • Response: Voting for labour in 1987 • Predictors 1 age, class, tenure, employment status 2 %unemployed, employment change, % in mining in 1981 • Expectation: coal mining areas vote for the left • Allow: mining parameters for mining effect(2) to vary over region(3) in a 3 -level logistic model

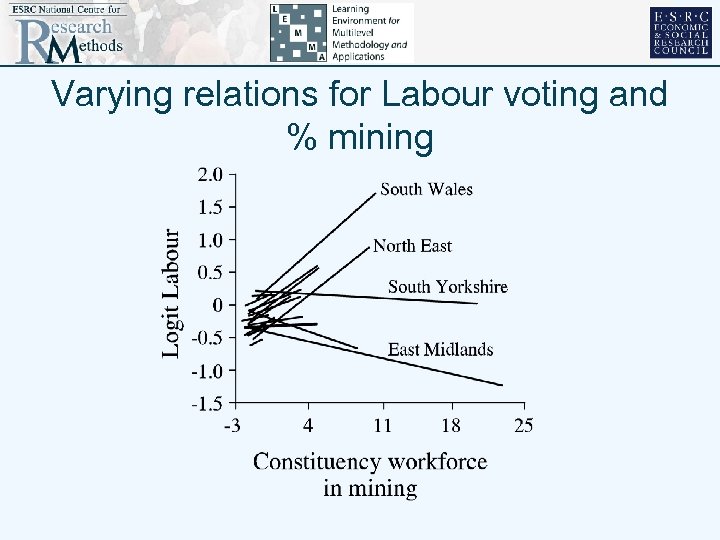Varying relations for Labour voting and % mining

Type of questions tackled by multilevel modelling I • 2 -level model: current attainment given prior attainment of pupils(1) in schools(2) • NB assuming a random sample of pupils from a random samples of schools • Do Boys make greater progress than Girls (F) • Are boys more or less variable in their progress than girls? (R) • What is the between-school variation in progress? (R) • Is School X different from other schools in the sample in its effect? (F) • continued…….

Type of questions tackled by multilevel modelling II • Are schools more variable in their progress for pupils with low prior attainment? (R) • Does the gender gap vary across schools? (R) • Do pupils make more progress in denominational schools? (F) • Are pupils in denominational schools less variable in their progress? (R) • Do girls make greater progress in denominational schools? (F) (cross-level interaction)

Workshop 2 • Draw a diagram relating a response (fat consumption) to a continuous predictor (age) centred around its national mean with the following characteristics no national relationship; substantial differences between seven 6 places in terms of the elderly, but less marked for middle-ages and least for young

Workshop 3 • Draw three separate graphs showing the following relations between response of house prices and a 3 -category predictor (detached, semi-detached, terrace) • a) differences between 3 categories of housing but no differences between places • b) differences between 3 categories of housing and same differences between places (random intercepts model) • c) differences between 3 categories of housing and different differences between places (random intercepts & slopes) • HINT: use different colours or line styles to show different places

Higher-level variables • So far all predictors have been level 1 (Math 3, boy/girl); (size, type of property) • Now higher level predictors (contextual, ecological) - global occurs only at the higher level; -aggregate based on summarising a level 1 attribute • Example: pupils in classes progress affected by previous score (L 1); class average score (A: L 2); class homogeneity (SD, A: L 2); teaching style (G: L 2) • NOW: trying to account for between school differences

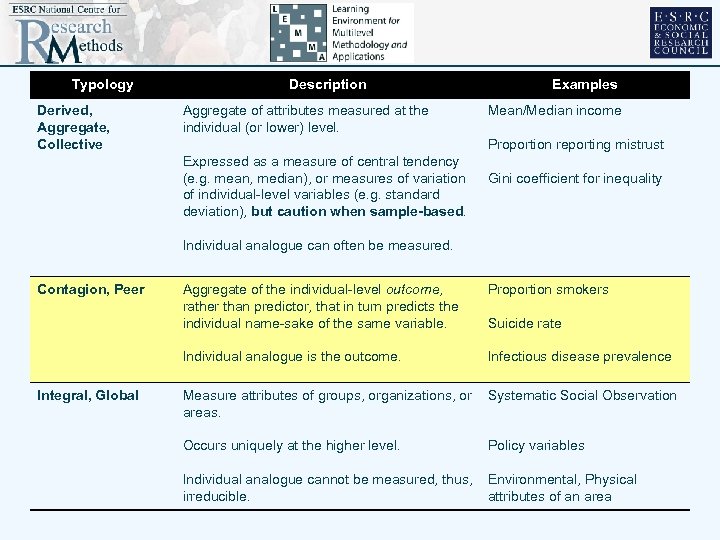Typology Derived, Aggregate, Collective Description Aggregate of attributes measured at the individual (or lower) level. Examples Mean/Median income Proportion reporting mistrust Expressed as a measure of central tendency (e. g. mean, median), or measures of variation of individual-level variables (e. g. standard deviation), but caution when sample-based. Gini coefficient for inequality Individual analogue can often be measured. Contagion, Peer Proportion smokers Individual analogue is the outcome. Integral, Global Aggregate of the individual-level outcome, rather than predictor, that in turn predicts the individual name-sake of the same variable. Infectious disease prevalence Measure attributes of groups, organizations, or areas. Systematic Social Observation Occurs uniquely at the higher level. Policy variables Individual analogue cannot be measured, thus, irreducible. Environmental, Physical attributes of an area Suicide rate

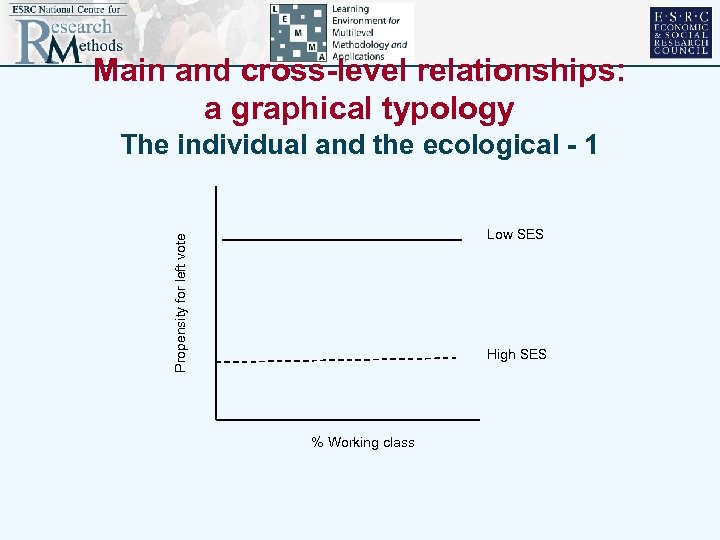Main and cross-level relationships: a graphical typology The individual and the ecological - 1 Propensity for left vote Low SES High SES % Working class

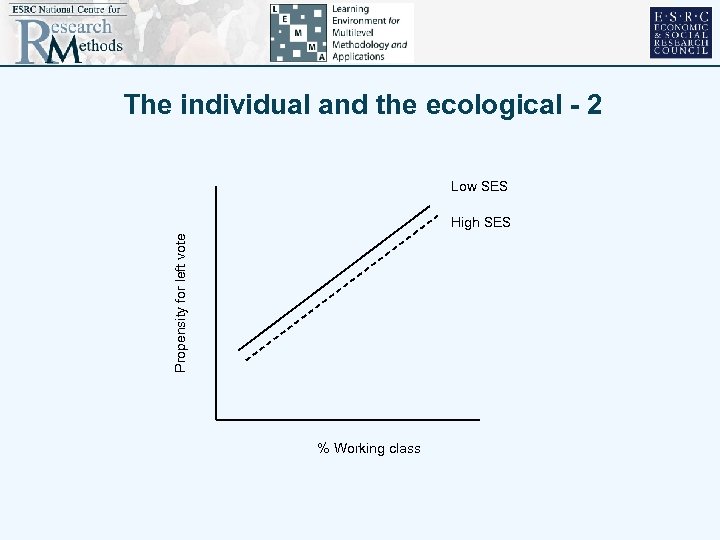The individual and the ecological - 2 Low SES Propensity for left vote High SES % Working class

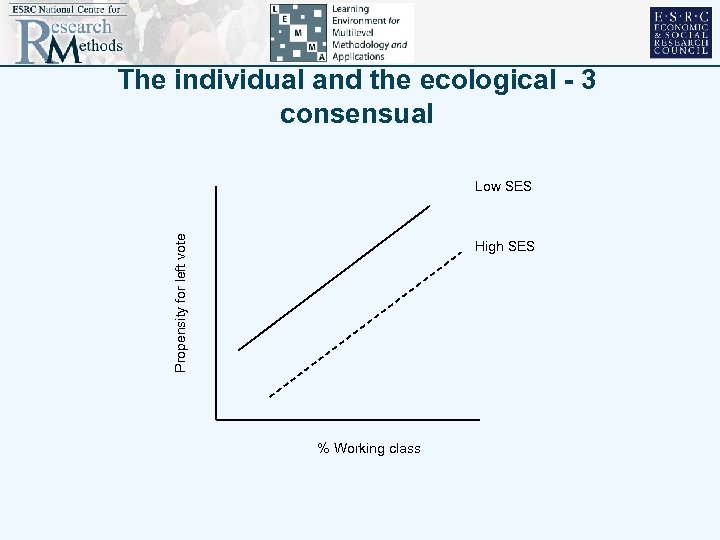The individual and the ecological - 3 consensual Propensity for left vote Low SES High SES % Working class

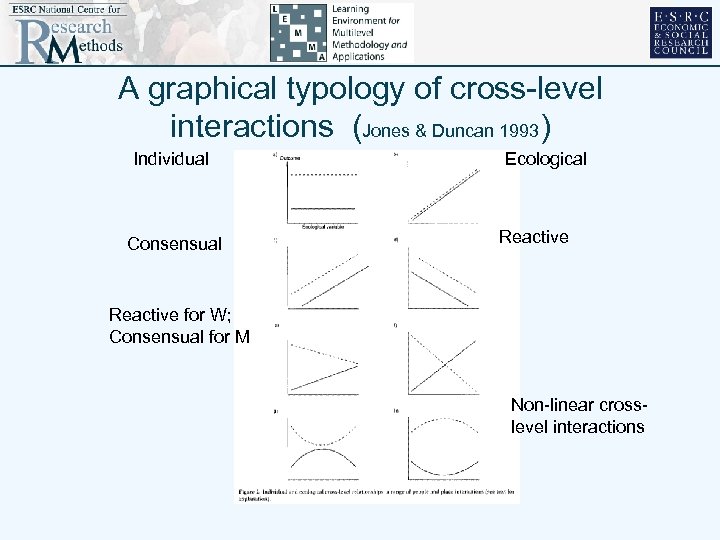A graphical typology of cross-level interactions (Jones & Duncan 1993) Individual Consensual Ecological Reactive for W; Consensual for M Non-linear crosslevel interactions

• • • - STRUCTURE: 2275 voters in 218 constituencies, 1992 RESPONSE: vote Labour not Conservative PREDICTORS: Level individual: age, sex, education, tenure, income 1 : 8 -fold classification of class - constituency: % Local authority renters 2 % Employers and managers; 100 - % Unemployed • MODEL: cross-level interactions between INDIVIDUAL&CONSTITUENCY characteristics Fixed part main effects: 8 fold division of class Random part at level 2: 2 fold division of class Working class: Non-working class: unskilled and skilled manual, foreman public and private-sector salariat, routine nonmanual, petty-bourgeoisie, ‘unstated’

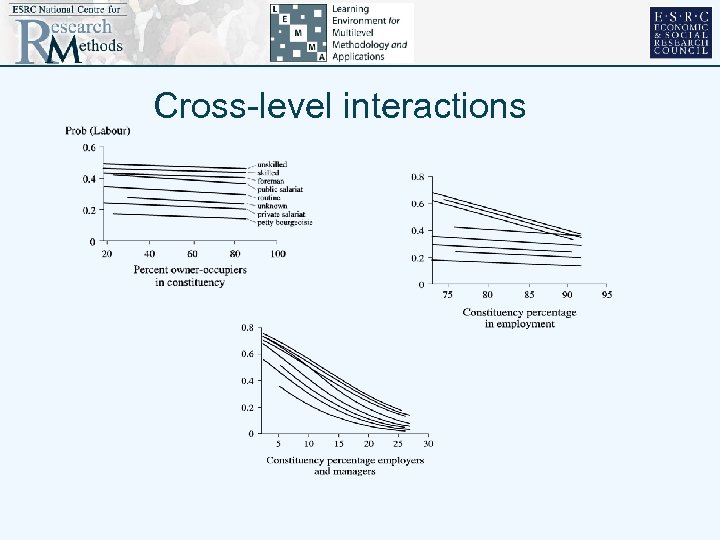Cross-level interactions

Conclusions 3 Substantive advantages 1 Modelling contextuality and heterogeneity 2 Micro AND macro models analysed simultaneously -avoids ecological fallacy and atomistic fallacy 3 Social contexts maintained in the analysis; permits intensive, qualitative research on ‘interesting’ cases “The complexity of the world is not ignored in the pursuit of a single universal equation, but the specific of people and places are retained in a model which still has a capacity for generalisation”

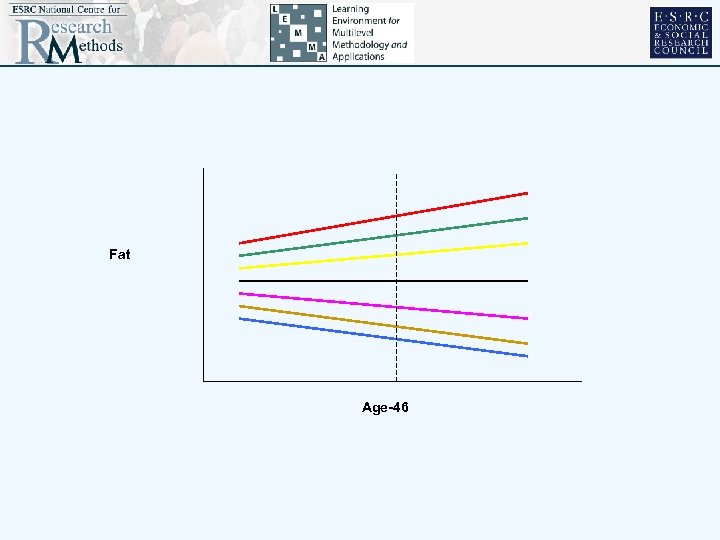Fat Age-46

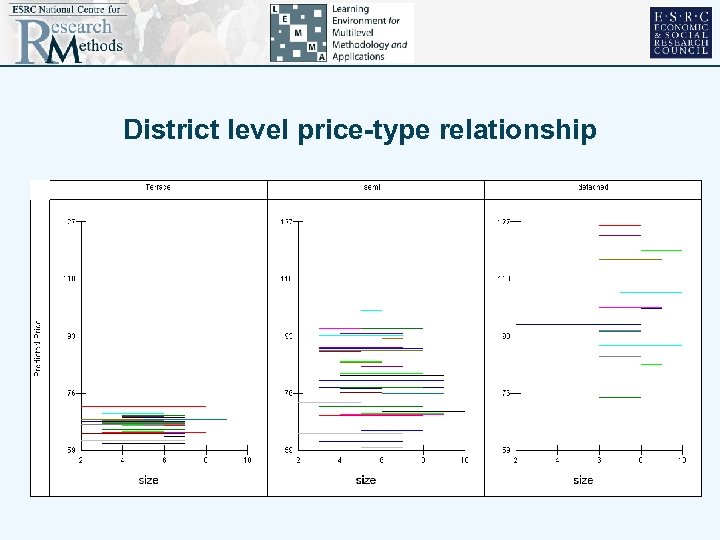District level price-type relationship