Working capital management Working capital cycle

Working capital management • Working capital cycle • Cash conversion cycle • The dynamics of working capital • Working capital policies • Overtrading • Cash management • Inventory management

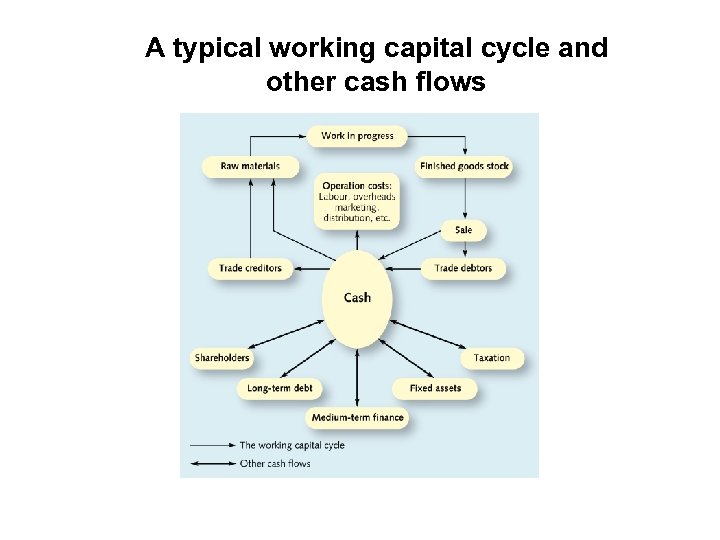A typical working capital cycle and other cash flows

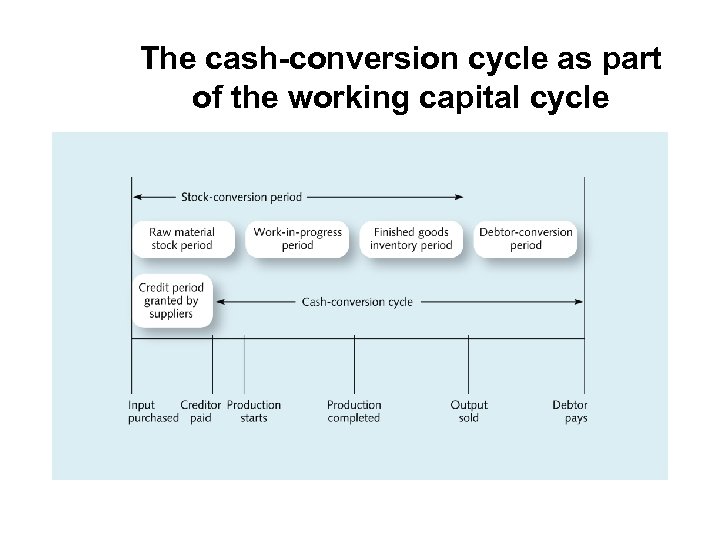The cash-conversion cycle as part of the working capital cycle

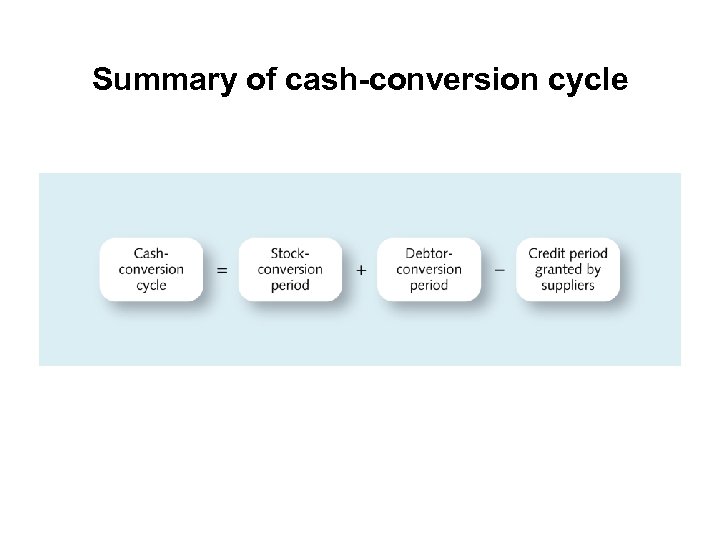Summary of cash-conversion cycle

Calculation of cash-conversion cycle Average value of raw materials stock Raw materials = ––––––––––––– = X days stock. Average usage of raw materials per day period Less Average level of creditors = ––––––––––––– = X days Purchases on credit per day Add Average value of work in progress = ––––––––––––– = X days period Average cost of goods sold per day Credit period Add Average value of finished goods in stock Finished goods = –––––––––––––– = X days inventory period Average cost of goods sold per day Add Average value of debtors Debtor-conversion = –––––––––––– = X days period Average value of sales per day Work-in-

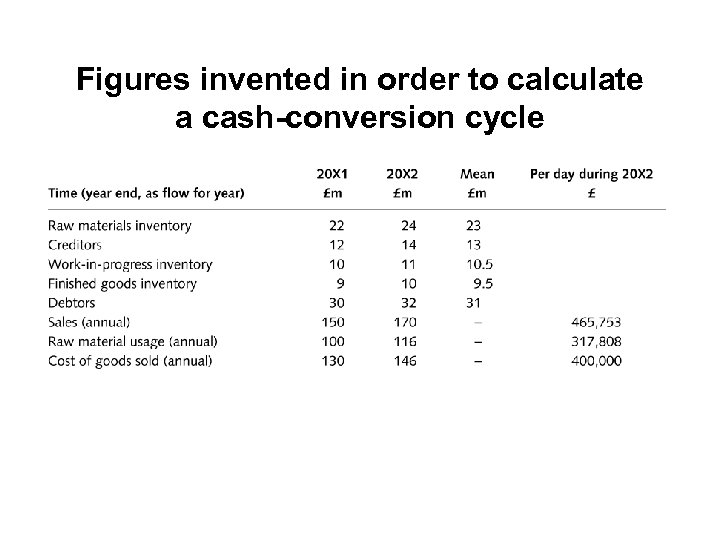Figures invented in order to calculate a cash-conversion cycle

Cash-conversion cycle

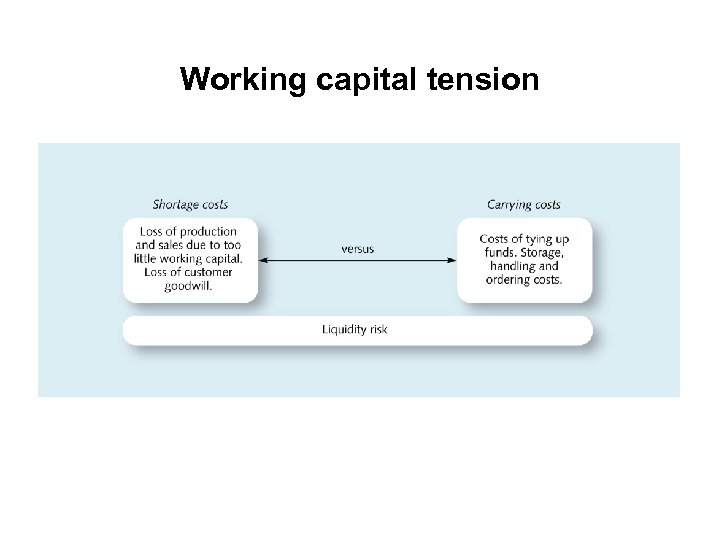Working capital tension

The dynamics of working capital

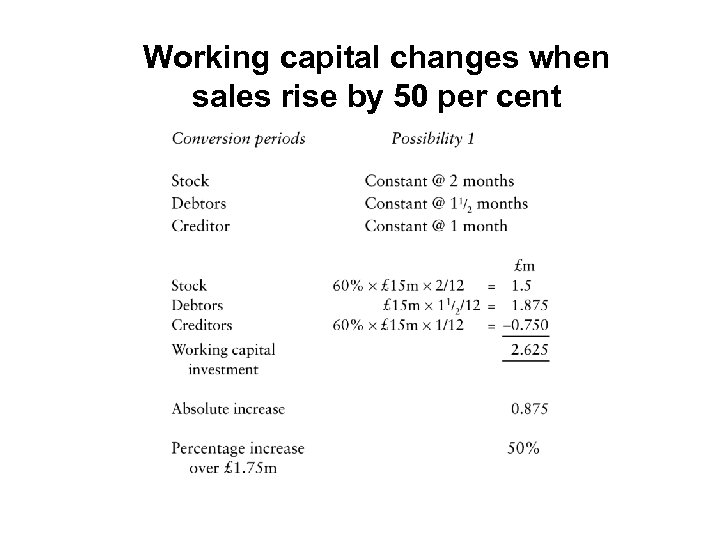Working capital changes when sales rise by 50 per cent

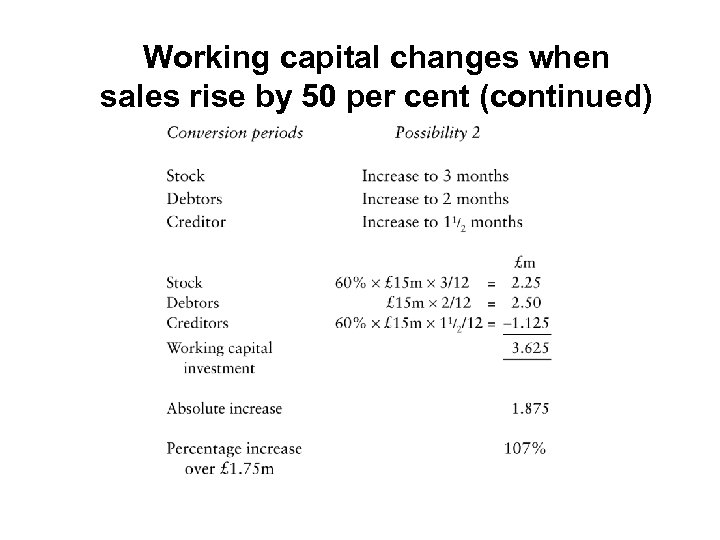Working capital changes when sales rise by 50 per cent (continued)

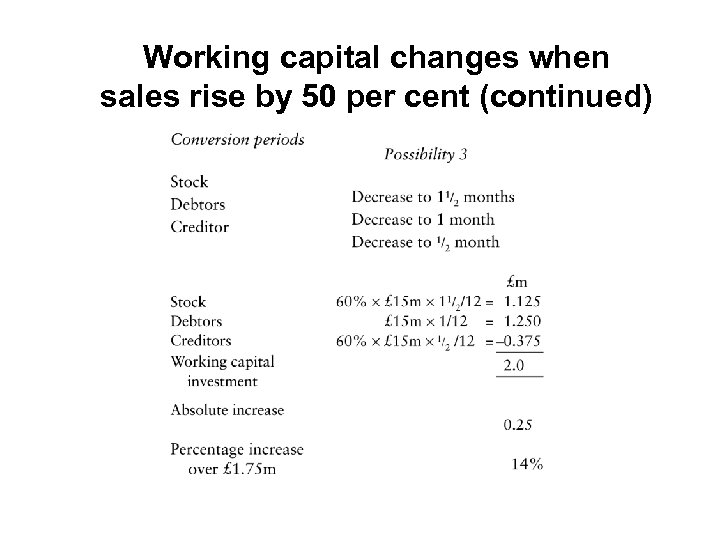Working capital changes when sales rise by 50 per cent (continued)

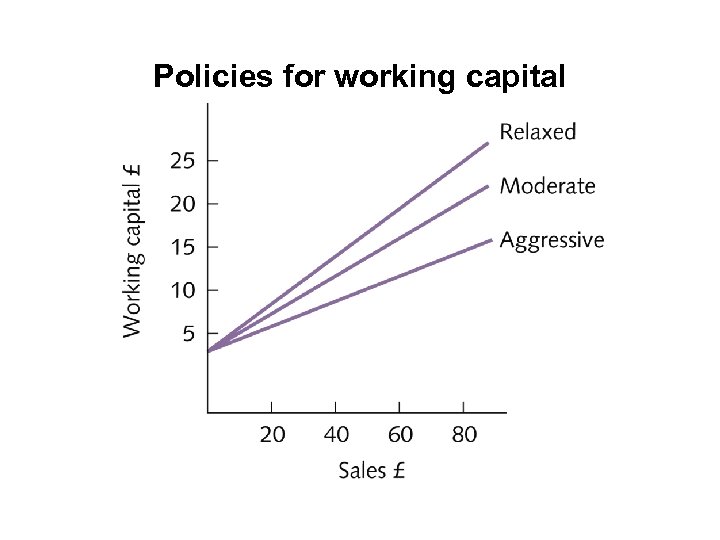Policies for working capital

Overtrading • Overtrading occurs when a business has insufficient finance for working capital to sustain its level of trading • A business is said to be overtrading when it tries to engage in more business than its working capital will allow • Bits and Rams Ltd which in 2004 had a turnover of £ 2 m and a profit of £ 200, 000: £ 000 Turnover 2, 000 Cost of goods sold 1, 800 –––––– 200 –––––– Profit

Cash flow for Bits and Rams Ltd in 2005

Why is cash important? • There are three categories of motives ascribed to the holding of cash: – 1 Transaction motive – 2 Precautionary motive – 3 Speculative motive • Operating cash is money held for operating purposes which is earning below-market interest rates because the firm needs quick access to it on a regular basis • Money held in cheque accounts is considered cash

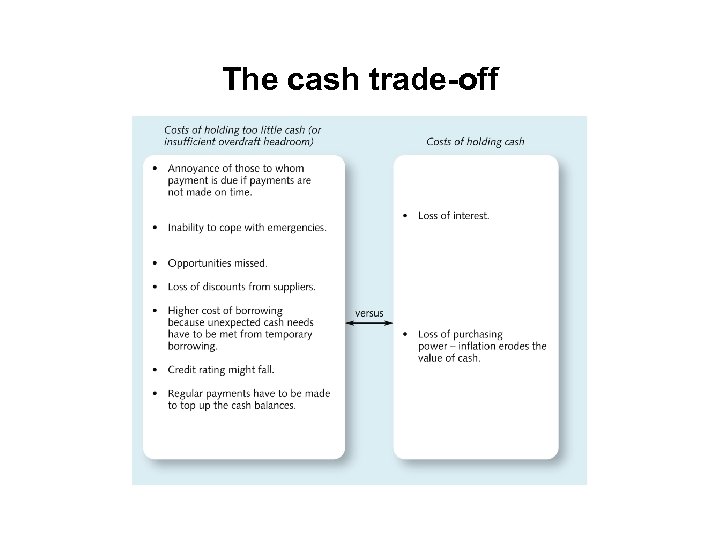The cash trade-off

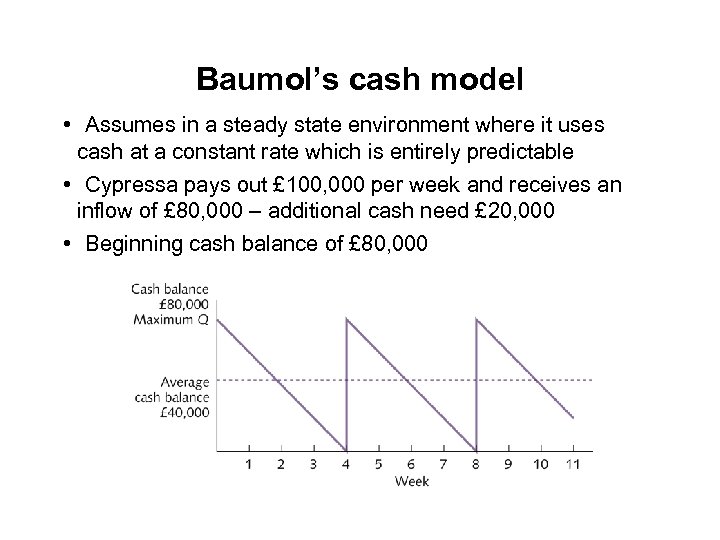Baumol’s cash model • Assumes in a steady state environment where it uses cash at a constant rate which is entirely predictable • Cypressa pays out £ 100, 000 per week and receives an inflow of £ 80, 000 – additional cash need £ 20, 000 • Beginning cash balance of £ 80, 000

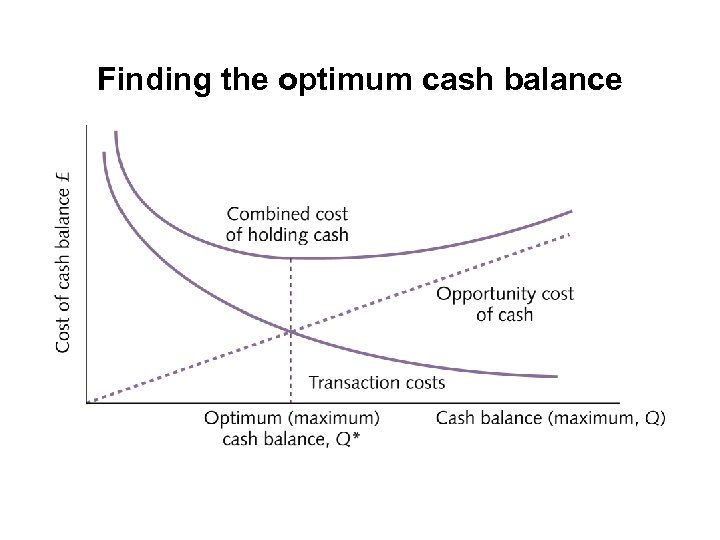Finding the optimum cash balance

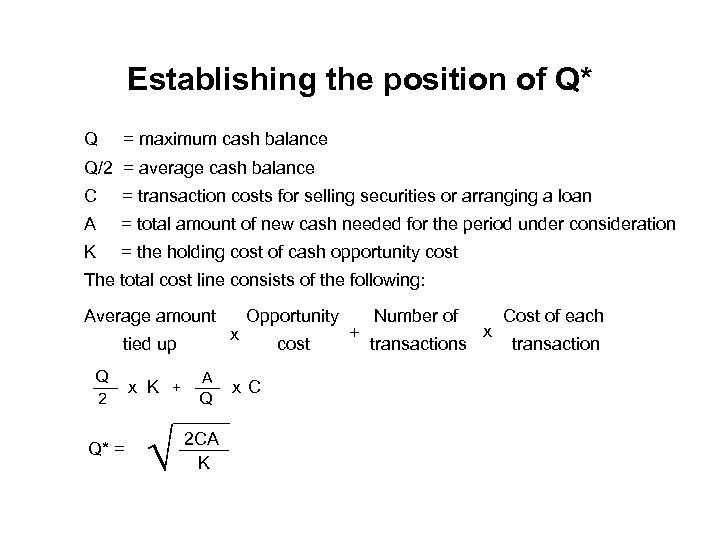Establishing the position of Q* Q = maximum cash balance Q/2 = average cash balance C = transaction costs for selling securities or arranging a loan A = total amount of new cash needed for the period under consideration K = the holding cost of cash opportunity cost The total cost line consists of the following: Average amount tied up Q 2 x K + Q* = Ö A Q 2 CA ––––– K x Opportunity x. C cost + Number of transactions x Cost of each transaction

Cypressa • Interest rate forgone, K, is 7 per cent • Annual need for cash is (£ 20, 000 × 52) = £ 1, 040, 000 Q* = Ö 2 × £ 500 × £ 1, 040, 000 ––––––––– = £ 121, 890 0. 07 • Number of times replenishment will take place each year: A/Q* = £ 1, 040, 000 / £ 121, 890

Some considerations for cash management • Create a policy framework – Establish a set of policies – Simpler and quicker decisions to be taken at lower levels in the organisation – Retain some flexibility for exceptional circumstances • Plan cash flows – Management need to know when cash is likely to be in surplus and when it is necessary to borrow – Volume and length of time of surpluses or deficits need to be known in advance to obtain the best terms and select the most appropriate instruments

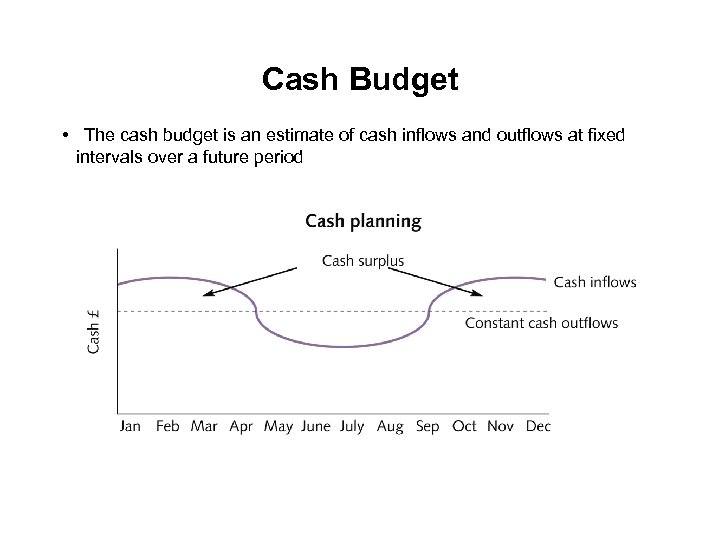Cash Budget • The cash budget is an estimate of cash inflows and outflows at fixed intervals over a future period

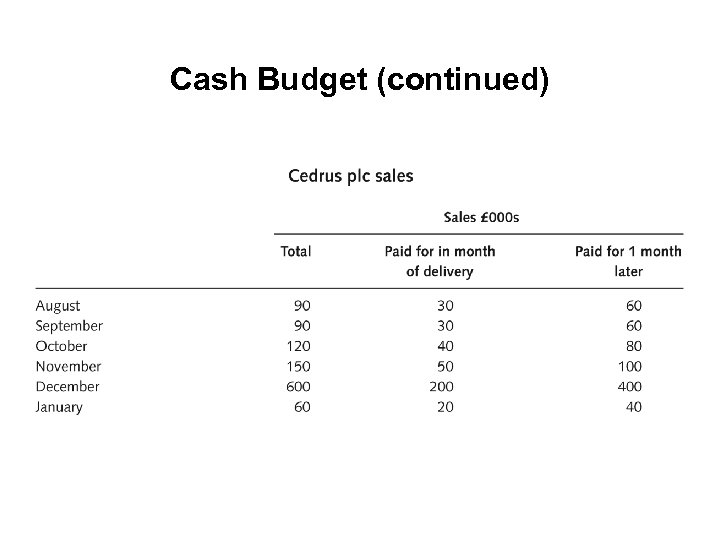Cash Budget (continued)

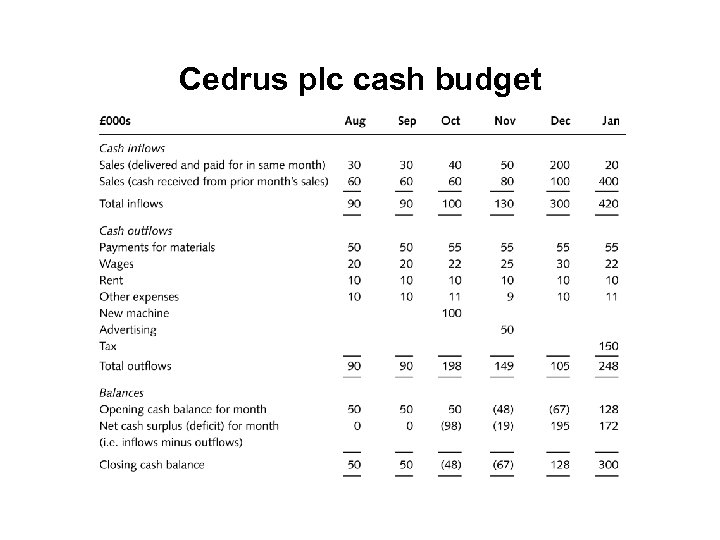Cedrus plc cash budget

Control cash flows • Firms have numerous bank accounts so that some banking transactions can take place near to the point of business • Problem: some bank accounts have high inflows others, high outflows • Firms need a co-ordinating system • Also an efficient mechanism is needed to funnel money to the centre • Cash flow synchronisation • Delays in the cheque-clearing system • The float is the difference between the cash balance shown on the firm’s cheque book and the bank account • Most banks offer an automated pooling of balances from many bank accounts into one master account

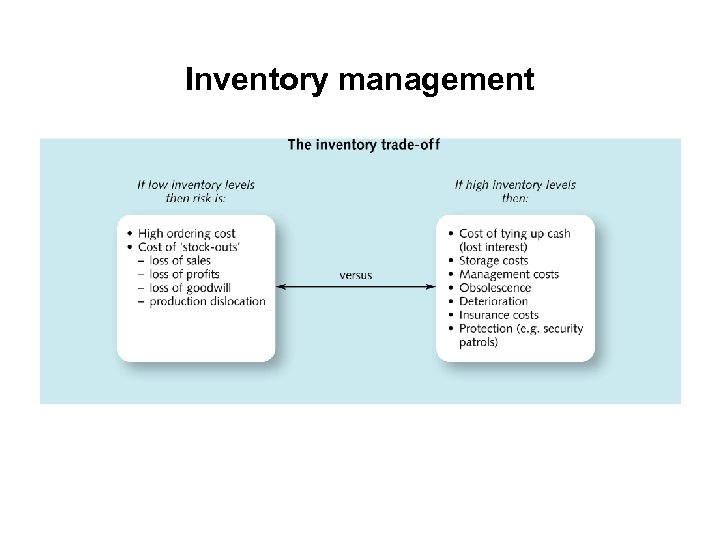Inventory management

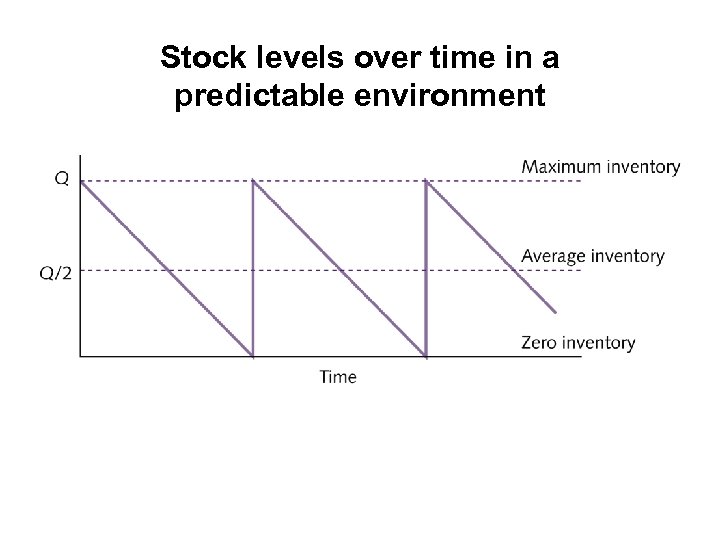Stock levels over time in a predictable environment

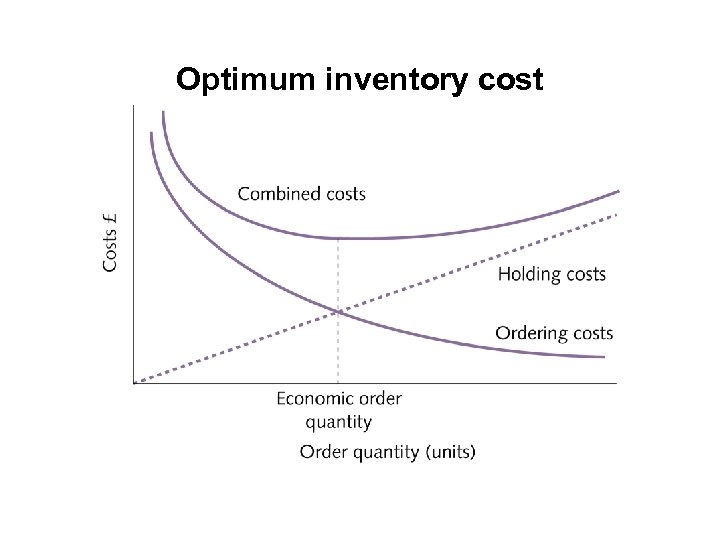Optimum inventory cost

Economic order quantity, EOQ • If C is the cost of placing each order, A is the annual usage of the inventory items, and H is the cost of holding one unit of stock for one year then: The annual ordering costs = Number of orders of per year x cost of each order = A/Q x C or AC Q The costs of holding stock = Average stock level (in units) x Cost of holding each unit per year = Q/2 x H HQ or 2 The total cost is: AC HQ + Q 2 EOQ = Ö 2 AC ––– H

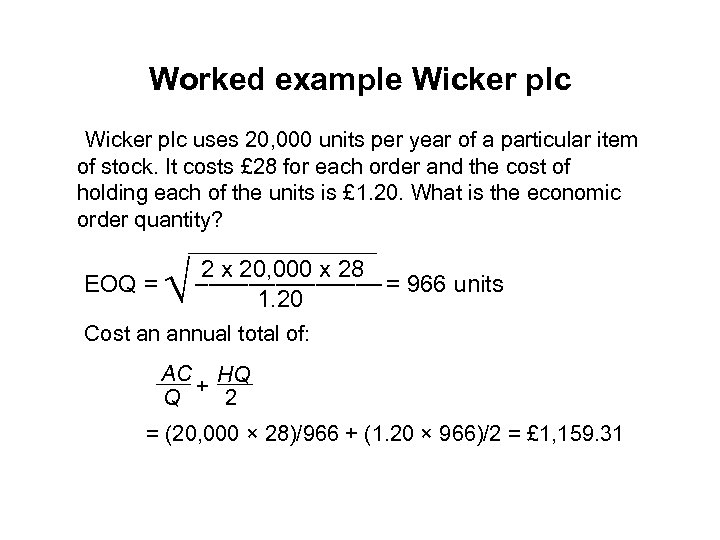Worked example Wicker plc uses 20, 000 units per year of a particular item of stock. It costs £ 28 for each order and the cost of holding each of the units is £ 1. 20. What is the economic order quantity? EOQ = Ö 2 x 20, 000 x 28 ––––––– = 966 units 1. 20 Cost an annual total of: AC HQ Q + 2 = (20, 000 × 28)/966 + (1. 20 × 966)/2 = £ 1, 159. 31

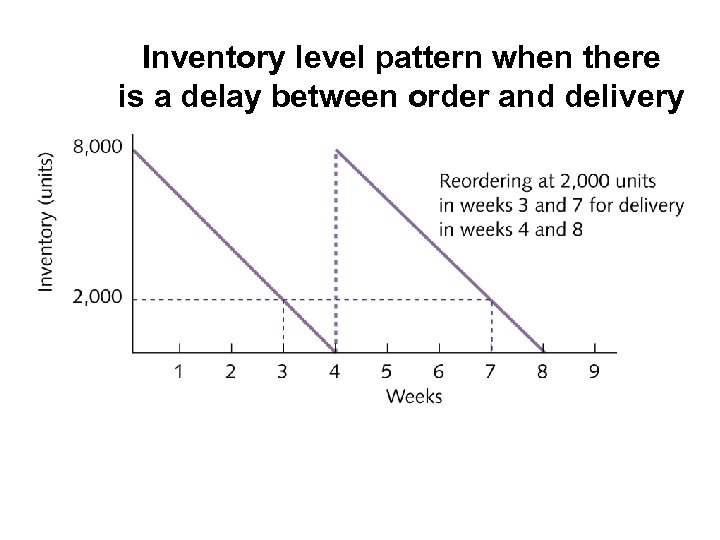Inventory level pattern when there is a delay between order and delivery

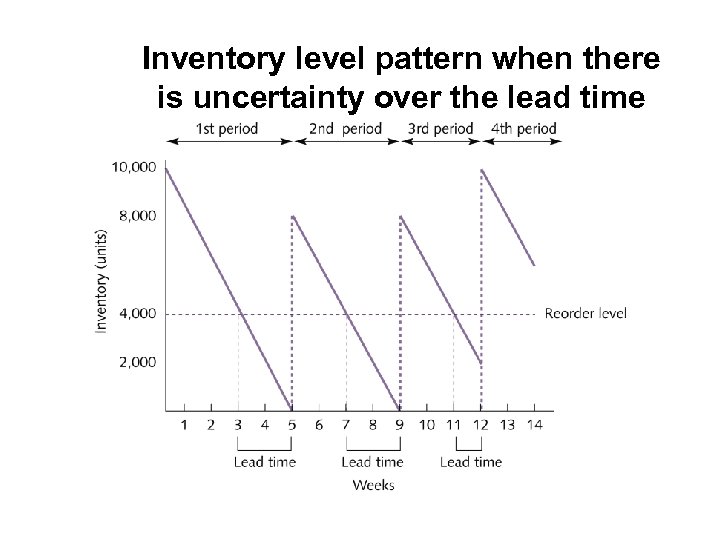Inventory level pattern when there is uncertainty over the lead time

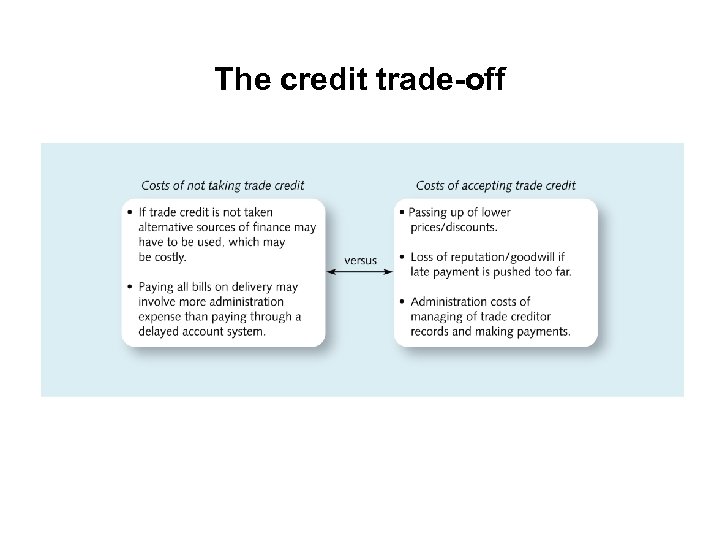The credit trade-off

The cost of capital • The cost of debt capital, both before and after tax considerations • The difficulties in estimating the equity cost of capital and the key elements that require informed judgement • The weighted average cost of capital (WACC) for a company • Evidence concerning how UK companies actually calculate the WACC • The outstanding difficulties in this area of finance

Cost of capital The cost of capital is the rate of return that a company has to offer finance providers to induce them to buy and hold a financial security. This rate is determined by the returns offered on alternative securities with the same risk • A word of warning – Behind any final number generated lies an enormous amount of subjective assessment – Good decision making comes from knowing the limitations of the input variables to the decision – Knowing where informed judgement has been employed in the cost of capital calculation is required to make value-enhancing decisions and thus assist the art of management – Precision is less important than knowledge of what is a reasonable range

The required rate of return • The capital provided to large firms comes in many forms • The rate of return offered on government bonds and Treasury bills is the bedrock rate that is used to benchmark other interest rates. It is called the risk-free rate of return, given the symbol rf • The cost of debt capital for a corporation k. D, is: k. D = rf + RP • If the current risk free rate is 6 per cent, then k. D = 7 per cent for a company paying 100 basis point over the Treasury rate • If the firm already has a high level of debt it may need to offer, say, 300 basis points above the risk-free rate k. D = rf + RP = 6 + 3 = 9%

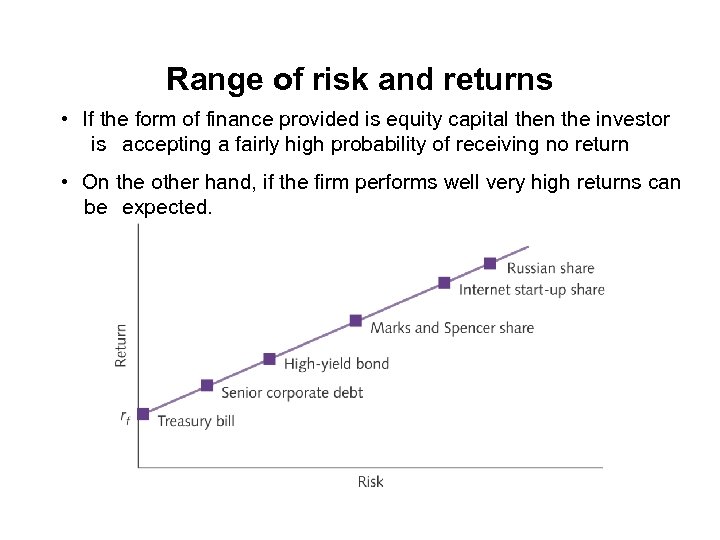Range of risk and returns • If the form of finance provided is equity capital then the investor is accepting a fairly high probability of receiving no return • On the other hand, if the firm performs well very high returns can be expected.

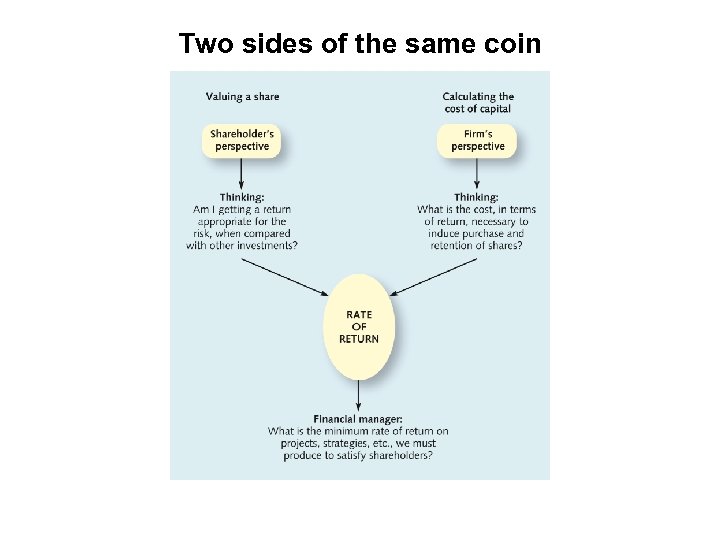Two sides of the same coin

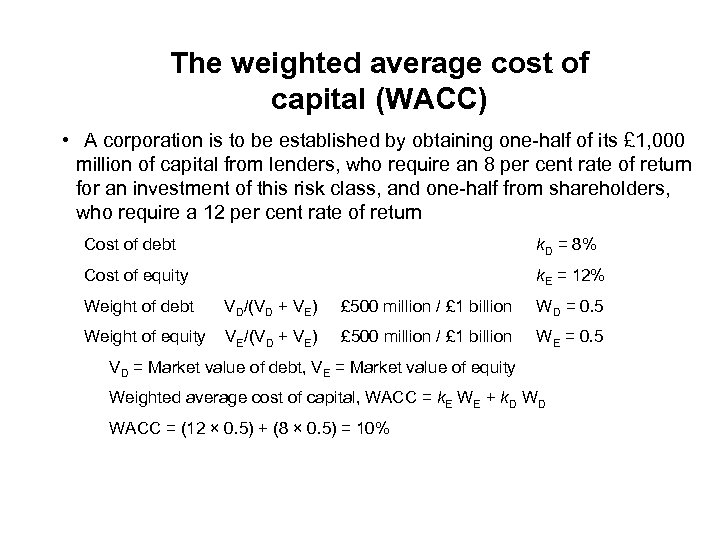The weighted average cost of capital (WACC) • A corporation is to be established by obtaining one-half of its £ 1, 000 million of capital from lenders, who require an 8 per cent rate of return for an investment of this risk class, and one-half from shareholders, who require a 12 per cent rate of return Cost of debt k. D = 8% Cost of equity k. E = 12% Weight of debt VD/(VD + VE) £ 500 million / £ 1 billion WD = 0. 5 Weight of equity VE/(VD + VE) £ 500 million / £ 1 billion WE = 0. 5 VD = Market value of debt, VE = Market value of equity Weighted average cost of capital, WACC = k. E WE + k. D WD WACC = (12 × 0. 5) + (8 × 0. 5) = 10%

Illustration of WACC • A firm invested £ 100, 000 in a project that produced a net cash flow per year of £ 10, 000 to infinity • Debt holders require £ 4, 000 per annum (8 per cent) • Leaves £ 6, 000 for equity holders – an annual return of 12 per cent on the £ 50, 000 they provided • An overall return of 10 per cent (the WACC) provides an 8 per cent return on the capital supplied by lenders and 12 per cent on the capital supplied by shareholders • A return of £ 11, 000 (i. e. 11 per cent) is generated • Debt holders receive £ 4, 000 • Equity holders get a 14 per cent return: £ 7, 000 on their £ 50, 000

Lowering the WACC and increasing shareholder returns • If the company is expected to produce £ 100 million cash flow per year (to infinity), and its WACC is 10 per cent, its total corporate value (‘enterprise’ value that is, the value of the debt and equity) is: £ 100 million / 0. 10 = £ 1, 000 million • Firm set up with 70 per cent debt WACC = k. EWE + k. DWD WACC = (12 × 0. 3) + (8 × 0. 7) = 9. 2% Firm value = £ 100 million /0. 092 = £ 1, 086. 96 million

Lowering the WACC? • If a rise in k. E exactly offset the benefit from the increase in the debt proportion; leaving the WACC constant WACC = k. E WE + k. D WD WACC = (14. 67 × 0. 3) + (8 × 0. 7) = 10% • Modigliani and Miller left out at least two important factors: – Tax – Financial distress

The benefit of tax

Lowering the WACC due to the tax shield k. DBT = Cost of debt before tax benefit = 8% k. DAT = Cost of debt after tax benefit = 8 (1 – T) = 8 (1 – 0. 30) = 5. 6% • If we assume a 50 : 50 capital structure the WACC is: WACC = k. E WE + k. DAT WD WACC = (12 × 0. 5) + (5. 6 × 0. 5) = 8. 8% • Investment project cash flows discounted at this lower rate will have a higher present value than if discounted at 10 per cent • This extra value flows to shareholders

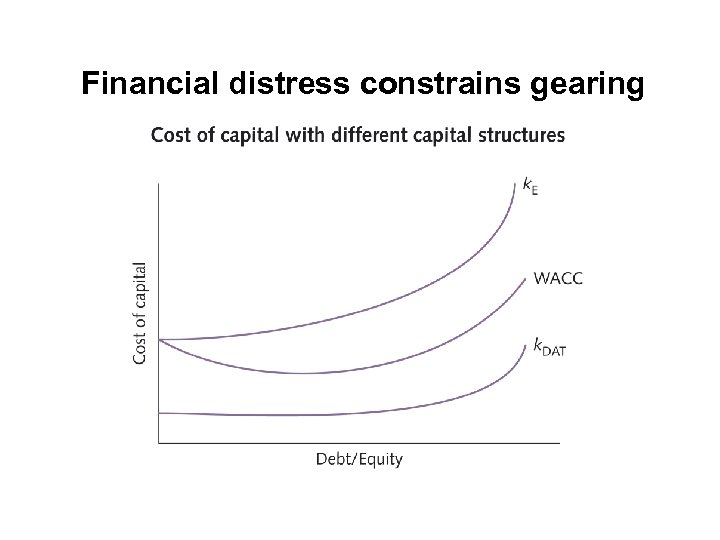Financial distress constrains gearing

WACC with tax and financial distress • The required return on equity rises from 12 per cent to 13 per cent when the proportion of the debt in the capital structure rises to 65 per cent • The effective rate of return payable on debt is 5. 6 per cent after the tax shield benefit • The WACC falls and the value available for shareholders rises WACC = k. E WE + k. DAT WD WACC = (13 × 0. 35) + (5. 6 × 0. 65) = 8. 19% • Assume that 65 per cent gearing is the optimum debt/equity ratio • If we go to 80 per cent debt we find this reduces shareholder wealth WACC = k. E WE + k. DAT WD WACC = (30 × 0. 2) + (7 × 0. 8) = 11. 6%

Worked example: Poise plc k. DBT = 10% k. E = 20% V = £ 2 m VE = £ 1. 4 m VD = £ 0. 6 m VE 1. 4 WE = ––– = 0. 7 V 2. 0 VD 0. 6 WD = ––– = 0. 3 V 2. 0

Poise: WACC calculation k. DAT = k. DBT (1 – T) k. DAT = 10 (1 – 0. 30) = 7% WACC = k. E WE + k. DAT WD = 20% × 0. 7 + 7% × 0. 3 = 16. 1% • An investment of £ 1 m at Time 0 produces after tax annual cash flows before interest payments of £ 161, 000 as a perpetuity a 16. 1 per cent rate of return • The net cost of satisfying the debt holders after the tax shield benefit is £ 21, 000 • Shareholders receive £ 140, 000 per year, a 20 per cent return on the £ 700, 000 they supplied • If the project produces £ 100, 000 the debt holders receive £ 21, 000, leaving only £ 79, 000 for the shareholders a mere 11. 3 per cent return

The cost of equity capital • Ordinary shareholders are not explicitly offered payments. However, there is an implicit rate of return Rate of return on shares = Risk-free rate + Risk premium k. E = rf + RP • Risk-free rate gives a return sufficient to compensate for both impatience to consume and inflation • To estimate the relevant risk premium on a firm’s equity we generally take two steps • Stage one is to estimate the average extra return demanded by investors above the risk-free return to induce them to buy a portfolio of average-risk level shares (rm – rf ) • Second stage is to adjust the risk premium for a typical (average-risklevel) share to suit the risk level for the particular company’s shares under consideration, (rm – rf) is multiplied by a systematic risk factor

The capital-asset pricing model (CAPM) • The risk premium has generally been adjusted by a beta based on the extent to which a share had moved when a market index moved k. E = rf + b (rm – rf ) • Beta is less than perfect

The Gordon growth model method for estimating the cost of equity capital • A company’s shares, priced at P, produce earnings of E per share and pay a dividend of d per share • The company has a policy of retaining a fraction, b, of its earnings each year • Under certain restrictive conditions, it can be shown that earnings, dividends and reinvestment will all grow continuously, at a rate of g = br, where r is the rate of return on the reinvestment of earnings d 1 P = –––––– k. E – g d 1 k. E = ––– + g P • We can derive g in other ways • Problem obtaining a trustworthy estimate of the future growth rate

Retained earnings and debt • The cost of retained earnings • The cost of debt capital The cost of debt is generally determined by the following factors: – The prevailing interest rates – The risk of default – The benefit derived from interest being tax deductible

Traded debt • UK bonds are normally issued with a nominal value of £ 100 n i Rn PD = –––––– + ––––––– t (1 + k. D)n t = 1 (1 + k. D) S i = annual nominal interest (coupon payment) Rn = amount payable upon redemption k. D = cost of debt capital (pre-tax benefit) PD = current market price of bond

Cost of traded debt example - Elm plc • Elm plc issued £ 100 m of bonds six years ago carrying an annual coupon rate of 8 per cent • Due to be redeemed in four years for the nominal value of £ 100 each • The next coupon is payable in one year and the current market price of a bond is £ 93 Year Cash flow 0 +£ 93 1 –£ 8 2 –£ 8 3 –£ 8 4 –£ 108 8 93 = –––––– + –––––––– + –––– 108 (1 + k )2 (1 + k )3 (1 + k )4 1+k D D

Elm plc With k. D at 11 per cent the discounted cash flow on the right hand side = 90. 69. With k. D at 10 per cent the discounted cash flow on the right hand side = 93. 66 – 93. 00 k. D = 10% + ––––––– ( 11 – 10) = 10. 22% 93. 66 – 90. 69 £ 93 VD = £ 100 m × ––––– = £ 93 m £ 100 • It would be wrong to use the coupon rate of 8 per cent on the bond for the cost of debt k. DAT = k. DAT (1 – T) k. DAT = 10. 22 (1 – 0. 30) = 7. 15%

Cost of finance • Financial Times, www. ic-community. co. uk/bonds, www. bondsonline. com • Untraded debt • Floating-rate debt • The cost of preference share capital d 1 Pp = ––– kp • Hybrid securities d 1 kp = ––– Pp

WACC • Calculating the weights – Book (accounting) values for debt, equity and hybrid securities should not be used in calculating the weighted average cost of capital. Market values should be used – Market capitalisation figure available in Monday editions of the Financial Times for quoted companies – also websites • The WACC with three or more types of finance WACC = k. EWE + k. DATWD + kp. Wp VE VD VP WE = ––––––– WD = ––––––– WP = ––––––– VE + V D + V P V E + VD + VP

WACC • Classic error: managers are sometimes tempted to use the cost of the latest capital raised to discount projects, SBUs, etc • What about short-term debt? – Should be included – However, to the extent that this debt is temporary or offset by cash and marketable securities it may be excluded • Finance and operating leases

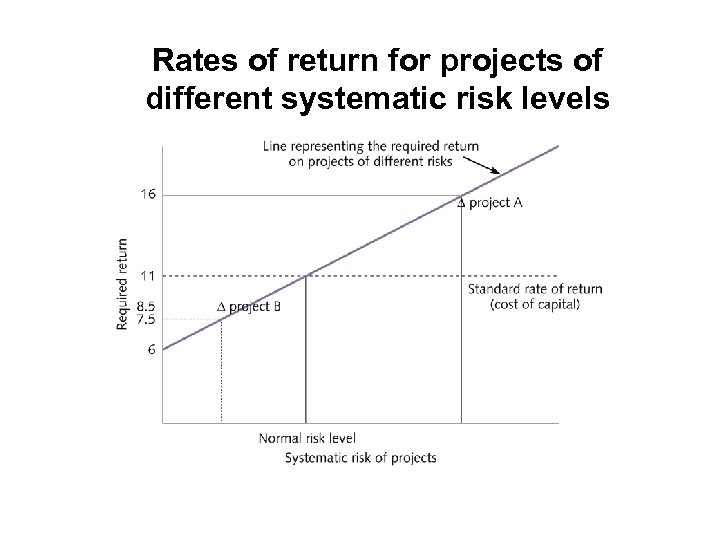Rates of return for projects of different systematic risk levels

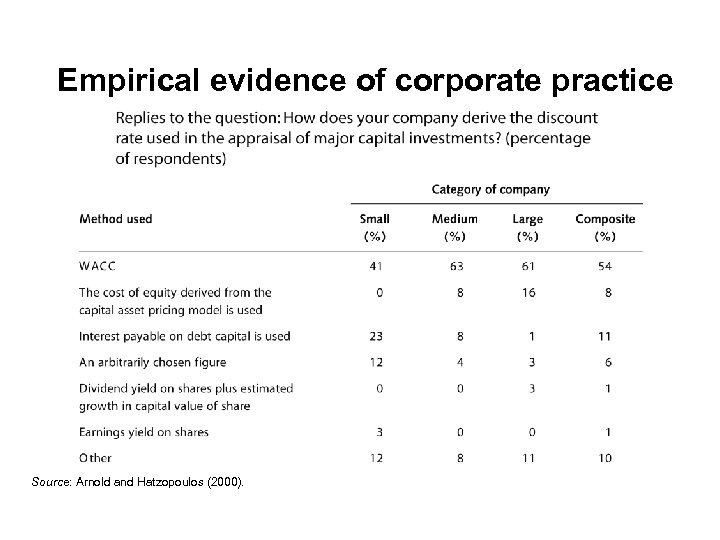Empirical evidence of corporate practice Source: Arnold and Hatzopoulos (2000).

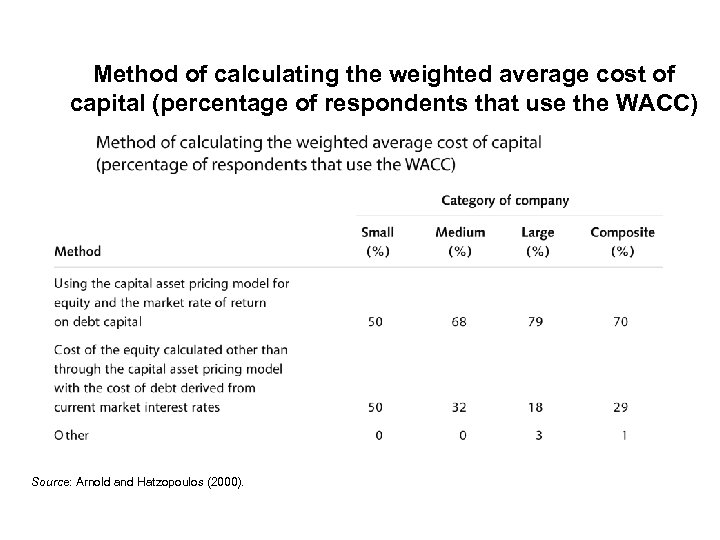Method of calculating the weighted average cost of capital (percentage of respondents that use the WACC) Source: Arnold and Hatzopoulos (2000).

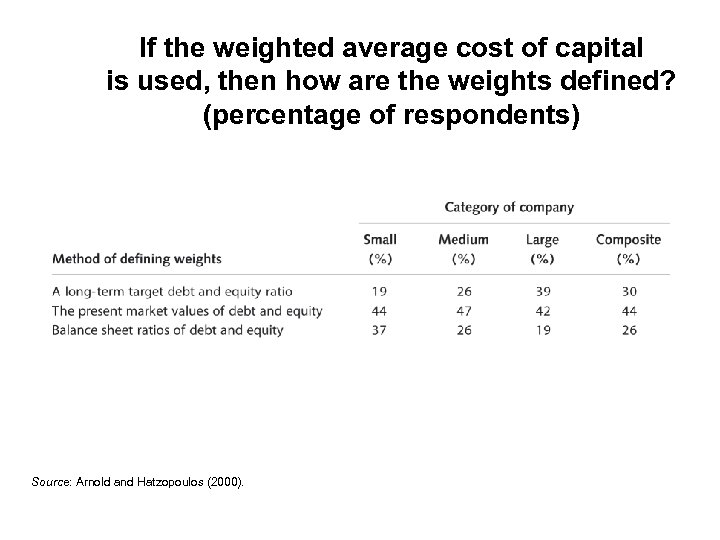If the weighted average cost of capital is used, then how are the weights defined? (percentage of respondents) Source: Arnold and Hatzopoulos (2000).

Gregory and Rutterford interviews • 14 companies made use of the CAPM to estimate the equity cost of capital, five used the dividend yield plus growth method • Four used the historic real rate of return on equity and five used more than one method • 12 out of 14 using the CAPM used the yield on UK government bonds as the risk-free rate • The remainder used a real (excluding inflation) rate of interest. None used the Treasury bill rate • Two out of the 13 firms which estimated an equity risk premium chose a figure from a mid-1990 s Barclays Capital Equity Gilt Study • 11 firms chose a number in a narrow range of 4. 5 per cent to 6 per cent

Gregory and Rutterford interviews • All 11 firms that explicitly consider the cost of debt allow for the corporate tax rate to reduce the effective cost • All the companies used the cost of long-term debt • The majority chose to base the cost of debt on the cost of government debt and either take this as the cost of debt or add a credit risk premium • Three companies took the yield on their own outstanding bonds and the remainder chose a long-term bond yield • Ten out of 15 firms that calculated the WACC used a long-run target debt/equity ratio, five used the actual debt/equity ratio and one used both • Ten companies chose to estimate a nominal WACC • Five used a real WACC and three used both a nominal and a real WACC • Corporations seem to make a distinction between the WACC and the hurdle rate

Implementation issues How large is the equity risk premium? • The equity risk premium is a subjective estimate. • In using historic data we are making at least two implicit assumptions: – There has been no systematic change in the risk aversion of investors over time. – The index being used as a benchmark has had an average riskiness that has not altered in a systematic way over time. • Differing views – Some City analysts – Plump for 2 per cent – Barclays Capital around 4 per cent, Competition Commission 3. 5 and 5 per cent, Ofgem 2. 5 per cent to 4. 5 per cent.

Implementation issues How reliable is CAPM’s beta? • The use of historic betas for future analysis • The breakdown in the relationship between beta and return Source: Thomson Financial Datastream.

Fundamental beta 1 The type of business that the company (SBU or project) is engaged in 2 Degree of operating gearing 3 Degree of financial gearing

Some thoughts on the cost of capital • Progress • Outstanding issues – The current risk-free rate is the bedrock – Return should be increased to allow for the risk of a share with average systematic risk – Risk premium increased or decreased depending on the company’s systematic risk level • Major difficulty calculating the systematic risk level

Capital structure: An introduction to the debate • Different types of gearing • The effect of gearing • Differentiate business and financial risk • The underlying assumptions, rationale and conclusions of Modigliani and Miller’s models in a world without tax

The balance between debt and ordinary share captial • Bristol Water announced plans to hand out £ 50 m of cash to shareholders in 2003 – ‘Bristol Water was overcapitalised and it was time to do something for the shareholders’ • In 2001 BT had accumulated debt of over £ 30 bn – Sir Peter Bonfield recognised that he had allowed the debt to rise too high. ‘We identified the need to introduce new equity capital into the business to support the reduction in the unsustainable level of group debt’ – Raised £ 5. 9 bn through a rights issue • Next implemented a share buy-back plan for up to 19 per cent of its shares in 2002, following the return of £ 435 m to shareholders through buy-backs in the 2000– 2 period – David Jones, chairman, said the share buy-backs represented the best way to enhance earnings per share

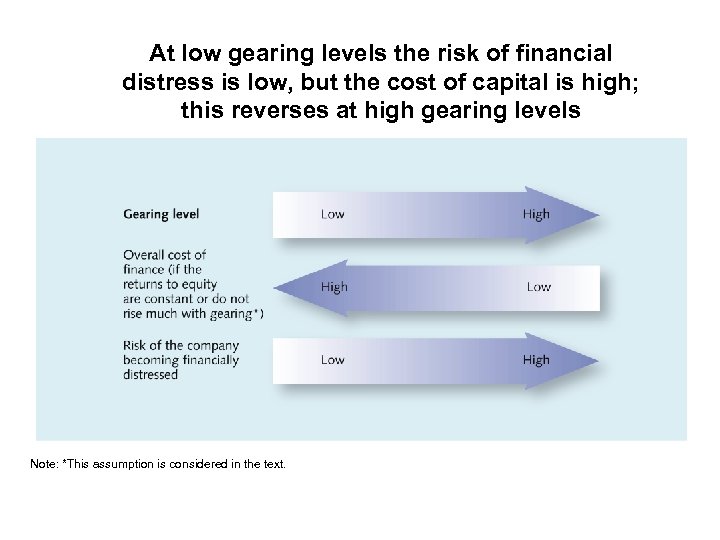At low gearing levels the risk of financial distress is low, but the cost of capital is high; this reverses at high gearing levels Note: *This assumption is considered in the text.

What do we mean by ‘gearing’? • Operating gearing refers to the extent to which the firm’s total costs are fixed • Financial gearing concerns the proportion of debt in the capital structure • Gearing and leverage are used interchangeably • Balance sheet (book) figures • Market values of debt and equity • Capital gearing focuses on the extent to which a firm’s total capital is in the form of debt • Income gearing is concerned with the proportion of the annual income stream (that is, the pre-interest profits) which is devoted to the prior claims of debtholders

Capital gearing (1) = Capital gearing (2) = Capital gearing (3) = Long-term debt Shareholders’ funds Long-term debt + Shareholders’ funds All borrowing + Shareholders’ funds Long-term debt Capital gearing (4) = Total market capitalisation

Income gearing • It may be erroneous to focus exclusively on assets when trying to judge a company’s ability to repay debts Profit before interest and tax Interest cover = –––––––––––––– Interest charges The inverse of interest cover measures the proportion of profits paid out in interest – this is called income gearing

The effect of gearing • If operating profits are high, the geared firm’s shareholders will experience a more than proportional boost in their returns compared to the ungeared firm’s shareholders • Harby plc is shortly to be established • Capital structures: – 1 All equity – 10 million shares sold at a nominal value of £ 1 – 2 £ 3 m debt (carrying 10 per cent interest) and £ 7 m equity – 3 £ 5 m debt (carrying 10 per cent interest) and £ 5 m equity

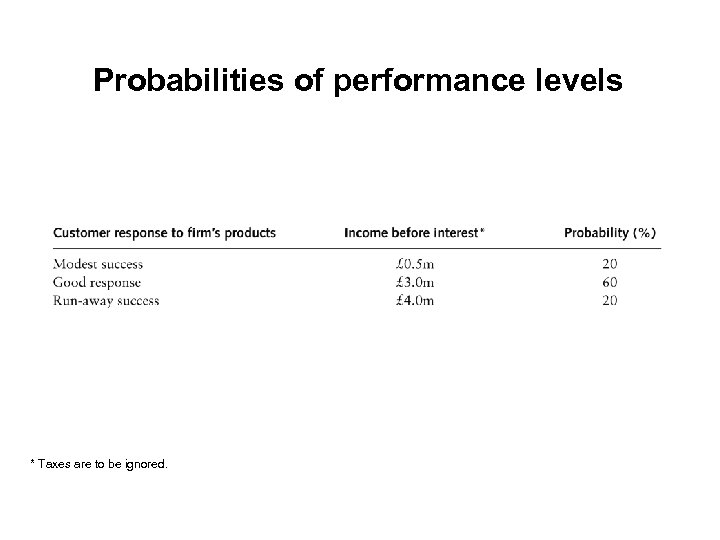Probabilities of performance levels * Taxes are to be ignored.

The effect of gearing

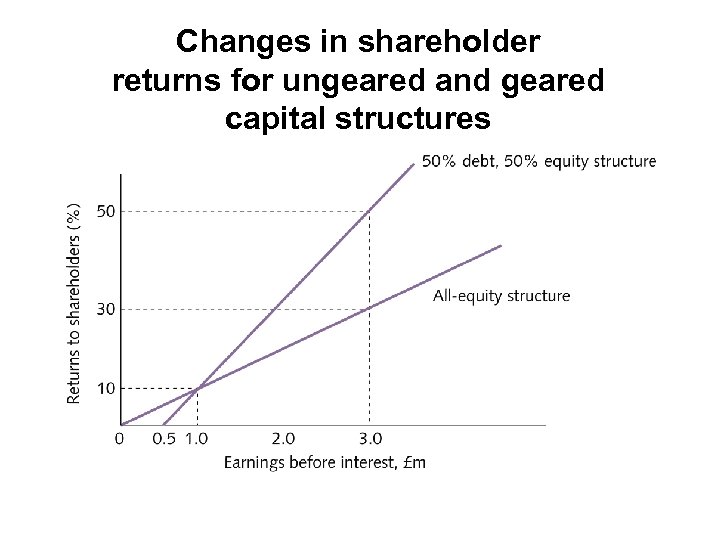Changes in shareholder returns for ungeared and geared capital structures

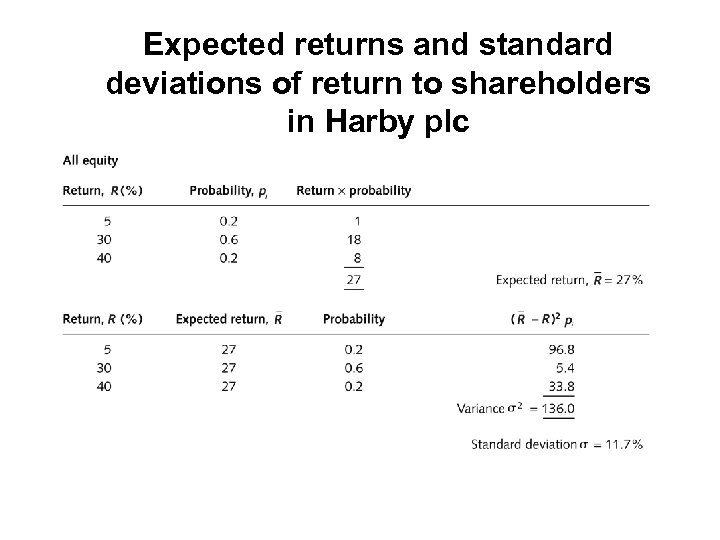Expected returns and standard deviations of return to shareholders in Harby plc

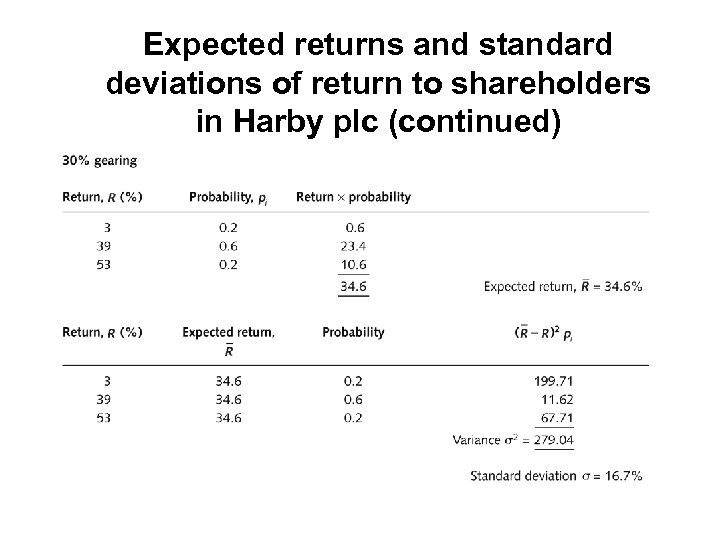Expected returns and standard deviations of return to shareholders in Harby plc (continued)

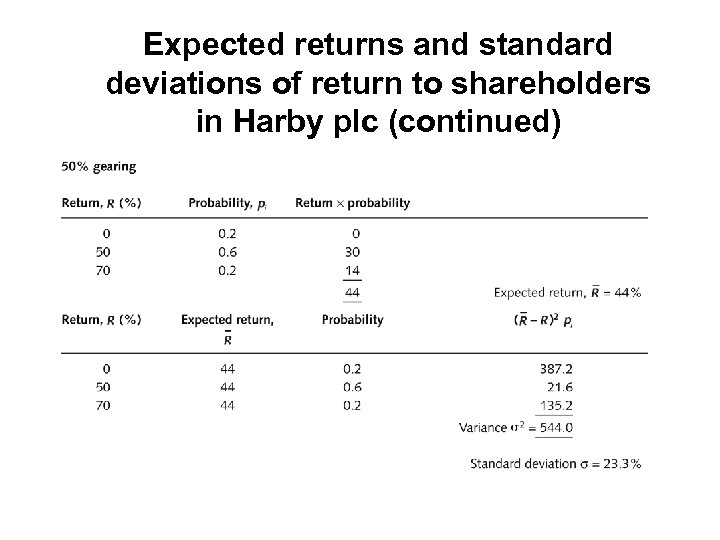Expected returns and standard deviations of return to shareholders in Harby plc (continued)

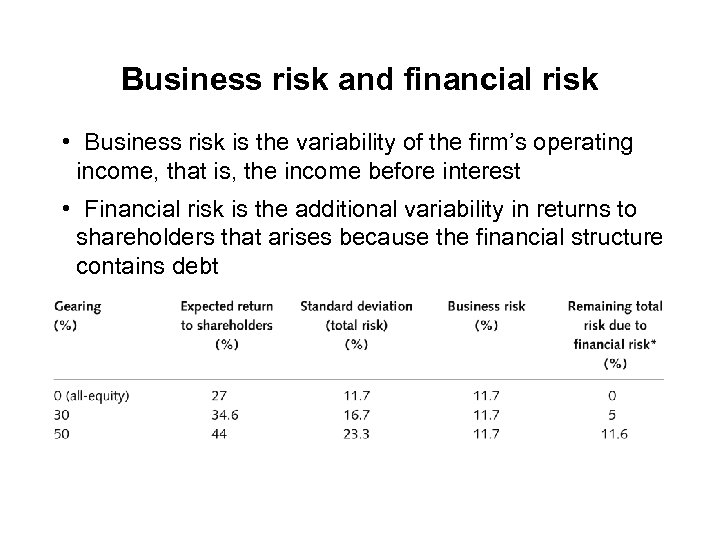Business risk and financial risk • Business risk is the variability of the firm’s operating income, that is, the income before interest • Financial risk is the additional variability in returns to shareholders that arises because the financial structure contains debt

The value of the firm and the cost of capital C 1 V = ––––––– WACC Value of the firm, V = VE + VD WACC = k. E WE + k. D WD Assume the cost of equity capital is 20 per cent, the cost of debt capital is 10 per cent, and the equity and debt weights are both 50 per cent WACC = (20% × 0. 5) + (10% × 0. 5) = 15% • The firm is expected to generate a perpetual annual cash flow of £ 1 m C 1 £ 1 m V = ––––– = £ 6. 667 m 0. 15 WACC

Does the cost of capital (WACC) decrease with higher debt levels? • Let us assume that the debt ratio is increased to 70 per cent through the substitution of debt for equity • Scenario 1 The cost of equity capital remains at 20 per cent WACC = k. E WE + k. D WD WACC = (20% × 0. 3) + (10% × 0. 7) = 13% C 1 £ 1 m V = ––––– = £ 7. 69 m WACC 0. 13 • Scenario 2 The cost of equity capital rises due to the increased financial risk to exactly offset the effect of the lower cost of debt WACC = k. E WE + k. D WD WACC = (26. 67% × 0. 3) + (10% × 0. 7) = 15%

Change the WACC • Scenario 3 The cost of equity capital rises, but this does not completely offset all the benefits of the lower cost of debt capital WACC = k. E WE + k. D WD WACC = (22% × 0. 3) + (10% × 0. 7) = 13. 6% C 1 £ 1 m V = ––––––– = £ 7. 35 m 0. 136 WACC • Scenario 4 The cost of equity rises to more than offset the effect of the lower cost of debt WACC = (40% × 0. 3) + (10% × 0. 7) = 19% C 1 £ 1 m V = ––––––– = £ 5. 26 m WACC 0. 19

Modigliani and Miller’s argument in a world with no taxes Proposition 1 • The total market value of any company is independent of its capital structure • The total market value of the firm is the net present value of the income stream. For a firm with a constant perpetual income stream: C 1 V = ––––––– WACC The WACC is constant because the cost of equity capital rises to exactly offset the effect of cheaper debt

MM: The assumptions 1 There is no taxation 2 There are perfect capital markets, with perfect information available to all economic agents and no transaction costs 3 There are no costs of financial distress and liquidation 4 Firms can be classified into distinct risk classes 5 Individuals can borrow as cheaply as corporations

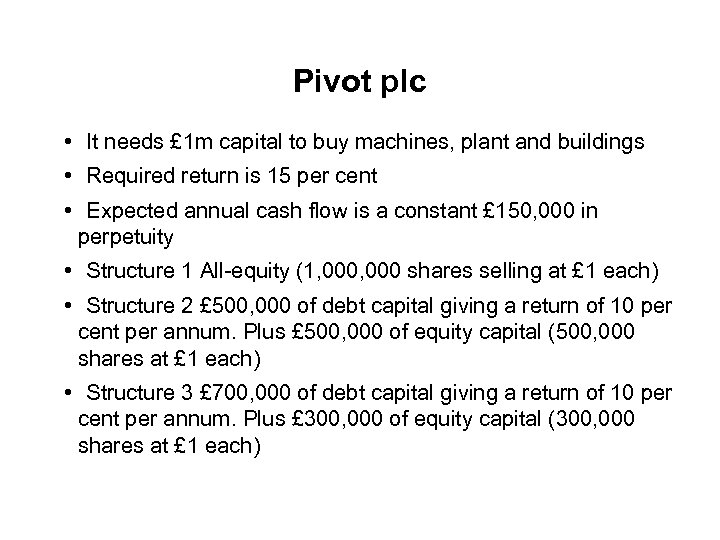Pivot plc • It needs £ 1 m capital to buy machines, plant and buildings • Required return is 15 per cent • Expected annual cash flow is a constant £ 150, 000 in perpetuity • Structure 1 All-equity (1, 000 shares selling at £ 1 each) • Structure 2 £ 500, 000 of debt capital giving a return of 10 per cent per annum. Plus £ 500, 000 of equity capital (500, 000 shares at £ 1 each) • Structure 3 £ 700, 000 of debt capital giving a return of 10 per cent per annum. Plus £ 300, 000 of equity capital (300, 000 shares at £ 1 each)

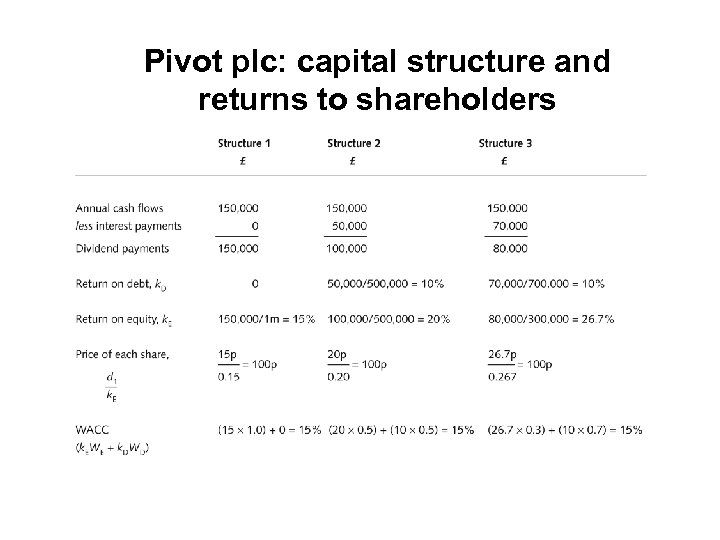Pivot plc: capital structure and returns to shareholders

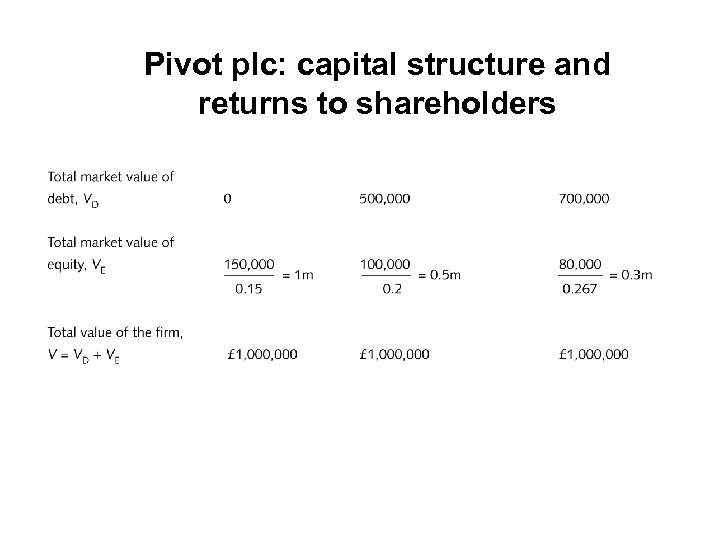Pivot plc: capital structure and returns to shareholders

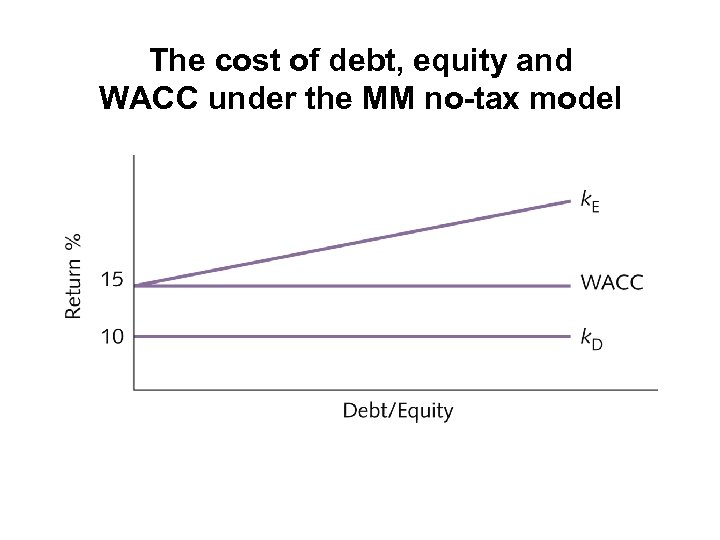The cost of debt, equity and WACC under the MM no-tax model

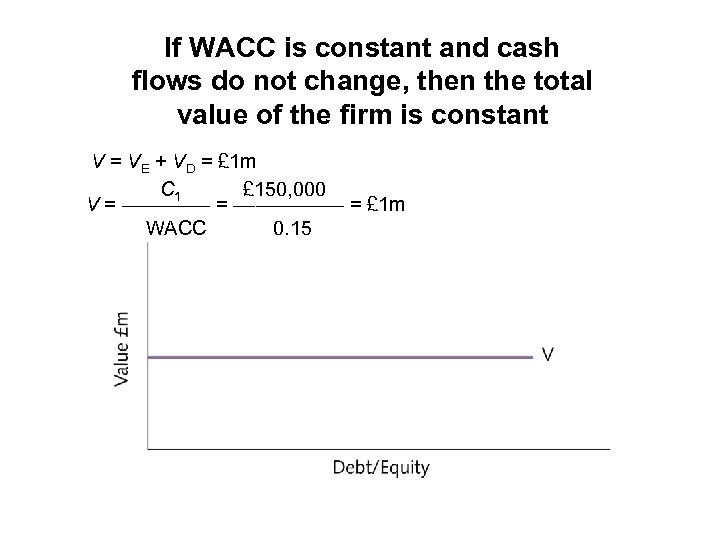If WACC is constant and cash flows do not change, then the total value of the firm is constant V = VE + VD = £ 1 m C 1 £ 150, 000 V = –––––––––– = £ 1 m WACC 0. 15

MM’s propositions • Proposition 2 – The expected rate of return on equity increases proportionately with the gearing ratio • Proposition 3 – The cut-off rate of return for new projects is equal to the weighted average cost of capital – which is constant regardless of gearing

Cost of equity capital for a geared firm that becomes an all-equity financed firm in a world with no taxes What would the cost of equity capital be if the firm described below is transformed into being all equity financed rather than geared? Perpetual future cash flow of £ 2. 5 m Market value of debt ––––––––––––––––––– = 0. 40 Market value of debt + Market value of equity k. D = 9% regardless of gearing ratio. At a gearing level of 40%, k. E = 22%. WACC = k. E WE + k. D WD WACC = (22 × 0. 6) + (9 × 0. 4) = 16. 8%

Capital structure: further considerations • Capital structure in a world with tax • Financial distress • Agency costs • Borrowing capacity • Managerial preferences • Pecking order • Financial slack • Signalling • Control • Industry group gearing • Motivation, reinvestment risk, operating and strategic efficiency

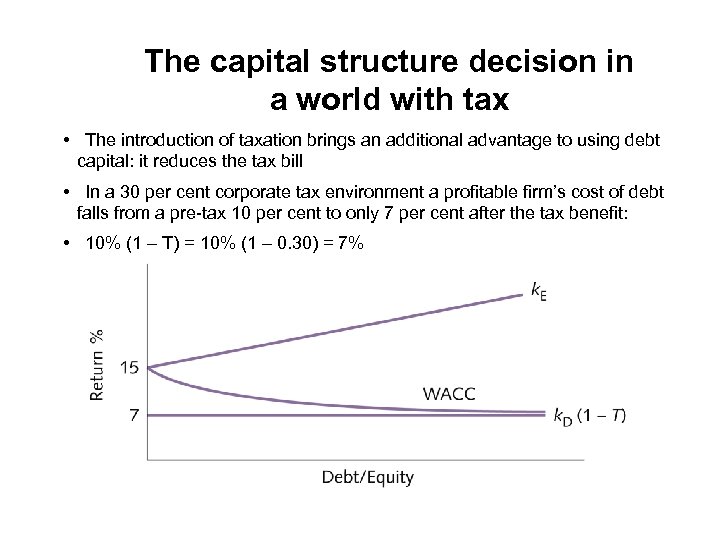The capital structure decision in a world with tax • The introduction of taxation brings an additional advantage to using debt capital: it reduces the tax bill • In a 30 per cent corporate tax environment a profitable firm’s cost of debt falls from a pre-tax 10 per cent to only 7 per cent after the tax benefit: • 10% (1 – T) = 10% (1 – 0. 30) = 7%

Financial distress: where obligations to creditors are not met or are met with difficulty.

Costs of financial distress

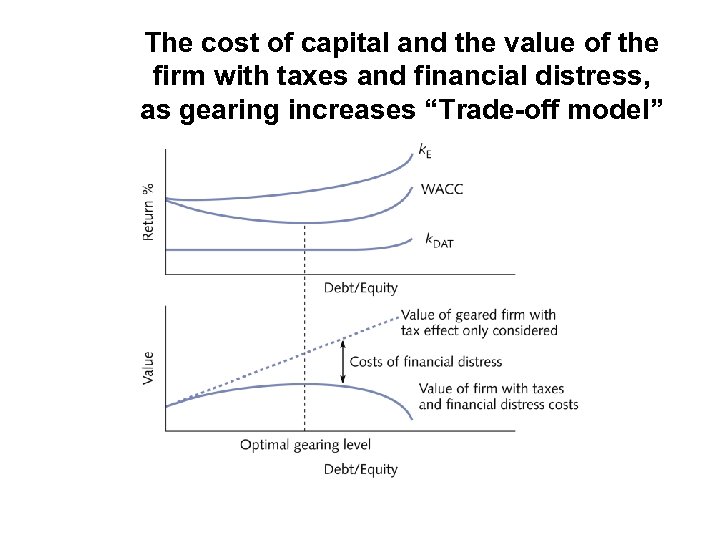The cost of capital and the value of the firm with taxes and financial distress, as gearing increases “Trade-off model”

Some factors influencing the risk of financial distress costs 1 The sensitivity of the company’s revenues to the general level of economic activity 2 The proportion of fixed to variable costs 3 The liquidity and marketability of the firm’s assets 4 The cash-generative ability of the business

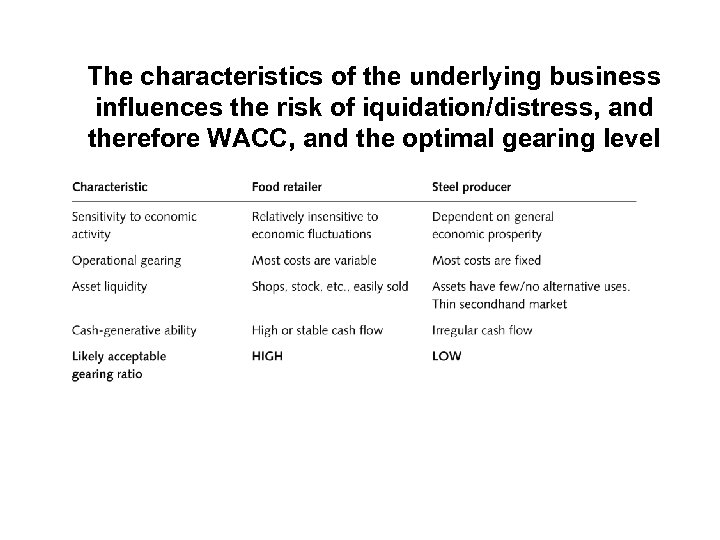The characteristics of the underlying business influences the risk of iquidation/distress, and therefore WACC, and the optimal gearing level

Agency costs • Agency costs are the direct and indirect costs of attempting to ensure that agents act in the best interest of principals as well as the loss resulting from failure to get them to act this way • Agency costs for lenders • Information asymmetry • Lenders will require a premium on the debt interest to compensate for the additional cost of monitoring • Restrictions (covenants) built into a lending agreement • Psychological element related to agency costs; managers do not like restrictions placed on their freedom of action

A few more factors • Borrowing capacity • Managerial preferences • Financial slack • Signalling • Control • Industry group gearing

Pecking order • Firms prefer to finance with internally generated funds • If still more funds are needed, the debt market is called on first • Only as a last resort will companies raise equity finance • Myers (1984): ‘In this story, there is no well-defined target debt–equity mix, because there are two kinds of equity, internal and external, one at the top of the pecking order and one at the bottom’ • Supposedly stock markets perceive an equity issue as a sign of problems – an act of desperation • Adverse selection problem • Line of least resistance • Shares are more expensive to issue than debt capital, which is more expensive than applying previously generated profits

Some further thoughts on debt finance • Motivation • Reinvestment risk • Operating and strategic efficiency

The WACC is U-shaped and value can be altered by changing the gearing level

Lecture review • The risk of financial distress • Short-term financing • Borrowing capacity • Gearing decisions • MM models • Financial slack, signalling, control, industry group gearing • High gearing motivates managers to perform • Reinvestment risk • Operating and strategic efficiency