Workflow Discovery from Empirical Data Laura Maruster Stefan

Workflow Discovery from Empirical Data Laura Maruster, Stefan Maruster, Silviu Nanau

Some question marks… § What is workflow management? § Why using Petri Nets? § What is wrong with today’s methods? § An overview of our method § Discussion and future development

What is Workflow Management? § It is the solution for problems as: § Controlling § Monitoring § Optimizing § Supporting a business process Many organizations with complex business processes have identified the need for concepts, techniques, and tools to support the management of work flows. Thus, the term of workflow management was born.

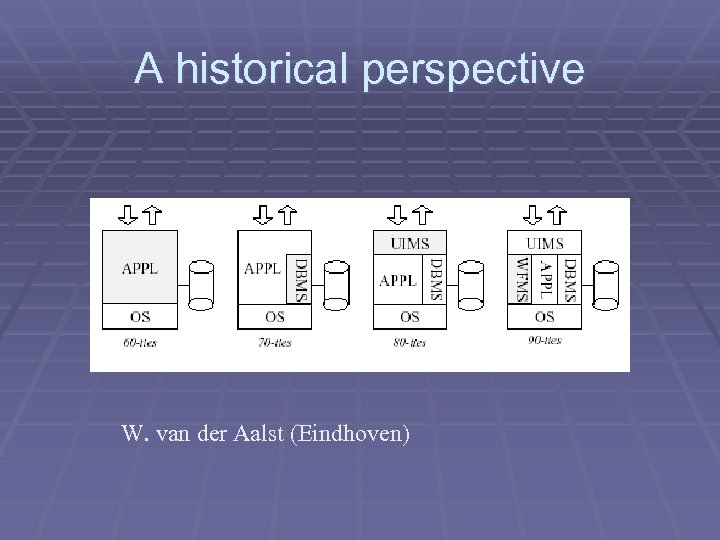A historical perspective W. van der Aalst (Eindhoven)

Why using Petri Nets? Four main reasons: § Possible mathematical model for complex processes (parallel branches) § Formal semantics despite the graphical nature. § State-based instead of event-based. § Abundance of analysis techniques.

What is wrong with today’s methods? § Takes a lot of time § Models are often incomplete § Models are not flexible enough

An overview of our method The basic idea of our algorithm supposes three main steps: § Identify the pairs (x, y) that are in direct succession according with an abstract preordering operator. § Using selected pairs (x, y) built a preliminary net. § Merge all places that have non-concurrent input or output transitions.

Step 1 § These pairs are put into tow sets: § The set of pairs where y appears after x, but x does not appear after y (R ) § The set of pairs where y appears after x, and x appears after y (R )

Step 2 Using pairs from R , built the preliminary net. At this stage, the selected pairs are connected and a place is inserted between the connected relations.

Step 3 Apply the following algorithm to build the final net, which merges all places that have non-concurrent input or output transitions. § N: =(P, T, F) § While M(N)≠Φ do (P 1, P 2)? M(N) N: =merge(N, {P 1, P 2}) od § NWL=N

Definitions 1. Let A be a set of observable actions. A workflow log is a set of sequences over A, i. e. WL A*, where A* is the set of all sequences that are composed of zero or more actions of A.

Definitions 2. For any sequence s A*, with s=(a 1, a 2, …, an) we have: § (s)={a 1, a 2, …, an} is the alphabet of s § (s)={(a 1, a 2), (a 1, a 3), …, (a 1, an), (a 2, a 3), …, (an-1, an)} § first(s)=a 1 § last(s)=an

Definitions 3. (R , ): Let WL be a workflow over A. We consider the following relations: § Let pref be the normal ordering on sequences and (a; b) the projection on {a; b}*. Define a preorder on A* which requires the relative order of elements a and b which are in conflict, i. e. , (a; b) I, to be the same when ignoring other elements of the sequences. Formally: u v if and only if ( (a; b) I: (a; b)(u) pref (a; b)(v))

Definitions 3 (cont. ) § R ={(x, y) A×A | s WL, (x, y) (s) s WL, (y, x) (s)}

Definitions 4. (N 0 WL) Let WL be a workflow log, and R , R Defined. Then: N 0 WL=(P, T, F) where as T= (s) s WL P=R {i, o} F={(i, t) (P×T)| s WL, t=first(s)} {(t, o) (T×P)| s WL, t=last(s)} {((x, y), t) (R ×T) | y=t, x y} {(t, (x, y)) (T×R )|x=t, x y} § § §

Definitions 5. Let N=(P, T, F) be a Petri net and X P a set of places. Then merge(N, X)=(P', T, F'), where § P'=(PX) {PX} § F'=F (P'×P') {(PX, t)}|t T p X, (p, t) F} {(t, PX)}|t T p X, (t, p) F}

Definitions 6. Let WL be a workflow log, N 0 WL and R as defined. § M(N): ={(P 1, P 2) P×P|(P 1 P 2 t 1 P 1, t 2 P 2, (t 1, t 2) R ) (P 1, P 2) P×P|( P 1 P 2 t 1 P 1 , t 2 P 2 , (t 1, t 2) R )} for any Petri net N=(P, T, F)

An Example Practically, we have a set of traces: § {s, f, h, g, i, k, o} § {s, b, c, d, e, j, o} §. . .

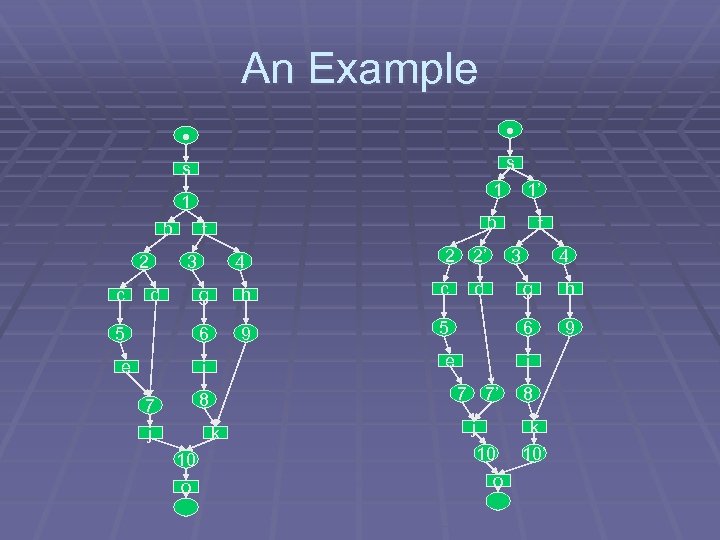An Example s s 1 1 b 2 c b f 3 4 2 2’ g 5 e h c 6 d 9 5 k f 3 4 g h 6 9 i 7 7’ 8 10 o d e i 7 j 1’ j 10 o 8 k 10’

Discussion § Preliminary work § Works well for sound WF without cycles § Future directions § Final goal: a robust tool

References § Laura Maruster – Automated discovery of Workflow § § § Models from Hospital Data K. Hayes and K. Lavery. Workflow management software: the business opportunity. T. M. Koulopoulos. The Workflow Imperative. Van Nostrand Reinhold, New York, 1995. W. M. P. van der Aalst. Three Good reasons for Using a Petri-net based Work on Management System. Proceedings of the International Working Conference on Information and Process Integration in Enterprises (IPIC 96), pp. 179: 201, Camebridge, Massachusetts, Nov 1996.

References § W. M. P. van der Aalst: The Application of Petri Nets to Workflow Management. The Journal of Circuits, Systems and Computers 1998 § C. A. Ellis, K. Keddara, G. Rozenberg. Dynamic Change within Workflow Systems. Conf. on Organizational Computing Systems, pp. 10: 21, ACM SIGOIS, Aug. 1995