318a43578b4aefd6e2bdf9dc5f4dee16.ppt
- Количество слайдов: 106

Work, Energy, and Power Lesson 1: Basic Terminology and Concepts – Definition and Mathematics of Work – Calculating the Amount of Work Done by Forces – Power – Potential Energy – Kinetic Energy – Internal Energy – Mechanical Energy Lesson 2 - The Work-Energy Relationship – Work-Energy Principle – Internal vs. External Forces – Analysis of Situations Involving External Forces – Analysis of Situations in Which Mechanical Energy is Conserved – Application and Practice Questions

Definition and Mathematics of Work force • In physics, work is defined as a _____ acting upon an object to ______ a cause displacement _________. • In order for a force to qualify as having done work on an object, there must be a displacement cause and the force must ______ the displacement Work done Work not done

Let’s practice – work or no work 1. A student applies a force to a wall and becomes exhausted. no work 2. A calculator falls off a table and free falls to the ground. work 3. A waiter carries a tray full of beverages above his head by one arm across the room no work 4. A rocket accelerates through space. work

Calculating the Amount of Work Done by Forces F θ • F - is the force in Newton, which causes the displacement of the object. • d - is the displacement in meters • θ = angle between force and displacement d Fy • W - is work in N∙m or Joule (J). 1 J = 1 N∙m = 1 kg∙m 2/s 2 F θ d • Work is a scalar quantity Fx • Work is independent of time the force acts on the object. Only the horizontal component of the force (Fcosθ) causes a horizontal displacement.

Example • How much work is done on a vacuum cleaner pulled 3. 0 m by a force of 50. 0 N at an angle of 30 o above the horizontal? .

Work for vertical motion • How much work is done in lifting a 5. 0 kg box from the floor to a height of 1. 2 m above the floor? Given: d = h = 1. 2 meters; m = 5. 0 kg; θ = 0 Unknown: W=? W = F∙dcosθ F = mg = (5. 0 kg)(9. 81 m/s 2) cos 0 o = 49 N W = F∙d = (49 N) (1. 2 m) = 59 J
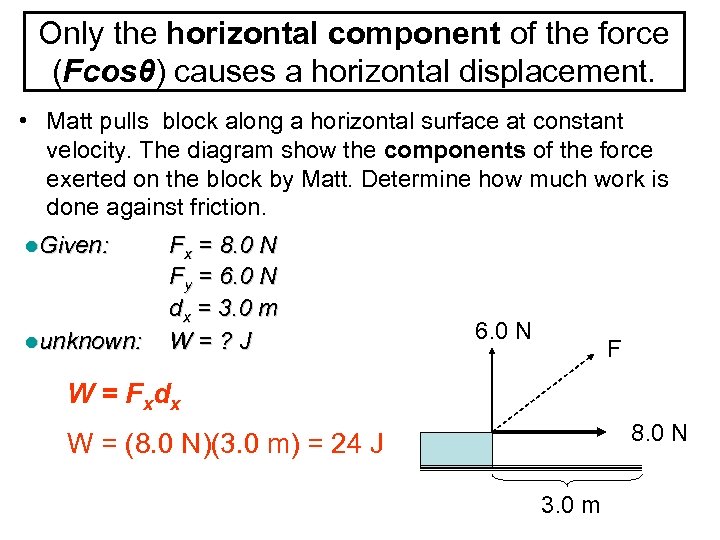
Only the horizontal component of the force (Fcosθ) causes a horizontal displacement. • Matt pulls block along a horizontal surface at constant velocity. The diagram show the components of the force exerted on the block by Matt. Determine how much work is done against friction. l. Given: lunknown: Fx = 8. 0 N Fy = 6. 0 N dx = 3. 0 m W=? J 6. 0 N F W = F xd x 8. 0 N W = (8. 0 N)(3. 0 m) = 24 J 3. 0 m

Relationships between work, force and displacement • A neighbor pushes a lawnmower four times as far as you do but exert only half the force, which one of you does more work and by how much? Wyou = Fd Wneighbor = (½ F)(4 d) = 2 Fd = 2 Wyou The neighbor, twice as much
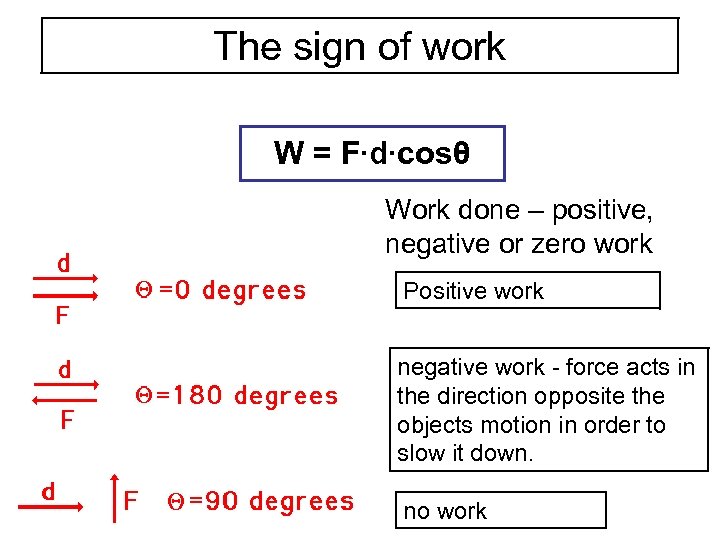
The sign of work W = F∙d∙cosθ Work done – positive, negative or zero work Positive work negative work - force acts in the direction opposite the objects motion in order to slow it down. no work

When F is ┴ to d, W = 0 To Do Work, Forces Must Cause Displacements On the force parallel to the displacement causes displacement W = F∙d∙cos 0 o = 0

Force vs. displacement graph Example: a block is pulled along a table with 10. N over a distance of 1. 0 m. W = Fd = (10. N)(1. 0 m) = 10. J height base area Force (N) • The area under a force versus displacement graph is the work done by the force. work Displacement (m)
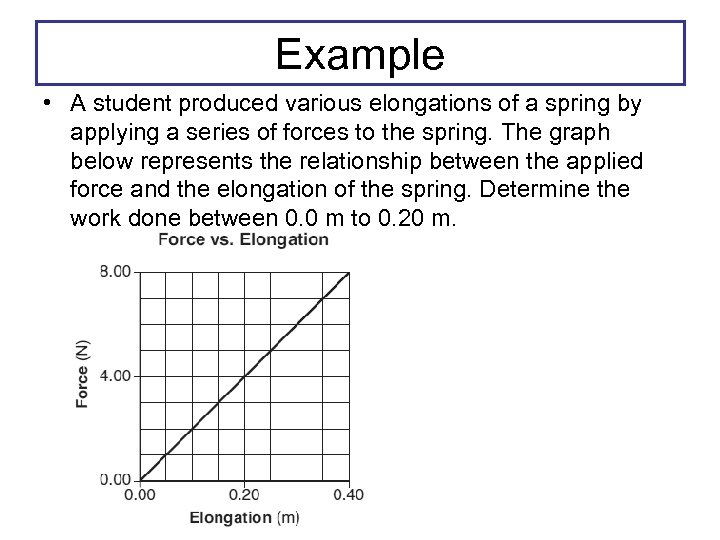
Example • A student produced various elongations of a spring by applying a series of forces to the spring. The graph below represents the relationship between the applied force and the elongation of the spring. Determine the work done between 0. 0 m to 0. 20 m.
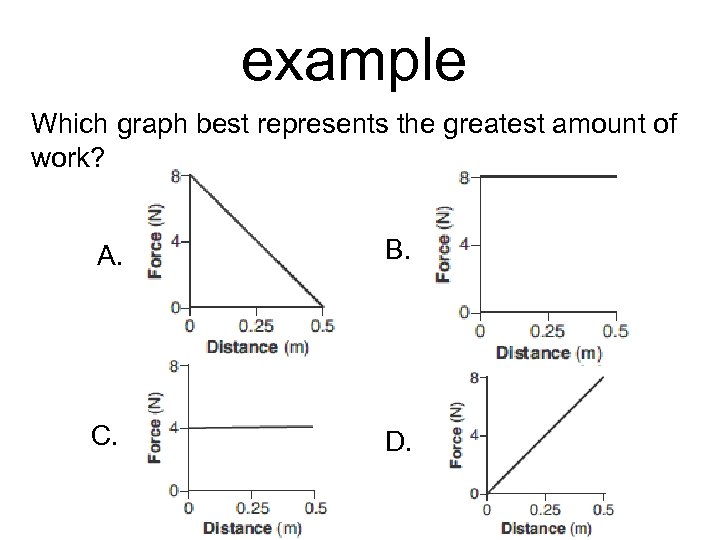
example Which graph best represents the greatest amount of work? A. B. C. D.
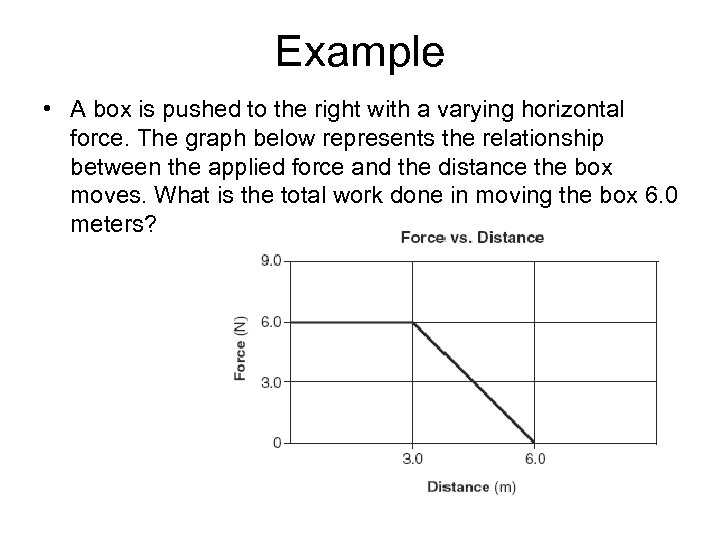
Example • A box is pushed to the right with a varying horizontal force. The graph below represents the relationship between the applied force and the distance the box moves. What is the total work done in moving the box 6. 0 meters?

The angle in work equation • The angle in the equation is the angle between the force and the displacement vectors. If F & d are in the same direction, θ is 0 o. d F
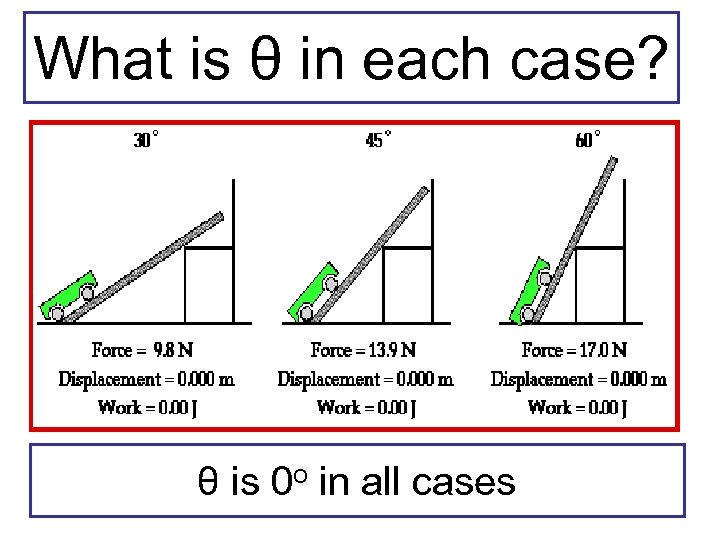
What is θ in each case? θ is 0 o in all cases

What have we learned? 1. What is definition of work? 2. What is the work equation? DAP to indicate variables in your equation. 3. Give examples of positive, negative and zero work 4. How to find work in F vs. d graph?

Power • Power is the rate at which work is done. It is the work/time ratio. Mathematically, it is computed using the following equation. • The standard metric unit of power is the Watt. All machines are typically described by a power rating. For example, a 60 Watt light bulb indicates 60 J of electrical energy is transferred to light energy every second. A high power car indicates that it can be accelerated very rapidly. Some people are more power-full than others because they are capable of doing the same amount of work in less time or more work in the same amount of time

example • Ben Pumpiniron elevates his 80 -kg body up the 2. 0 -meter stairwell in 1. 8 seconds. What is his power? It can be assumed that Ben must apply an (80 kg x 9. 81 m/s 2) -Newton downward force upon the stairs to elevate his body.

Another equation for power

example • Two physics students, Will N. Andable and Ben Pumpiniron, are in the weightlifting room. Will lifts the 100 -pound barbell over his head 10 times in one minute; Ben lifts the 100 -pound barbell over his head 10 times in 10 seconds. Which student does the most work? _______ Which student delivers the most power? _______ Explain your answers.

example • When doing a chin-up, a physics student lifts her 42. 0 -kg body a distance of 0. 25 meters in 2 seconds. What is the power delivered by the student's biceps?

kilowatt-hour is unit for energy • Your household's monthly electric bill is often expressed in kilowatt-hours. One kilowatt-hour is the amount of energy delivered by the flow of l kilowatt of electricity for one hour. Use conversion factors to show many joules of energy you get when you buy 1 kilowatt-hour of electricity.

Work and Energy are related • When work is done on a system, that system’s change in energy equals to the amount of work done on it. • Work and energy have the same unit: Joule • For example, if you push a cart, you do work on the cart, the cart is going to speed up and its temperature may increase, its energy is increased. If you lift a rock, you do work on the rock and you increase the rock’s energy. • There are many forms of energy. – Potential energy – Kinetic energy – Internal energy
Potential energy • An object can store energy as the result of its position. Potential energy is the stored energy of position possessed by an object. • Two form: – Gravitational – Elastic

Gravitational potential energy 1. When you lift an object, you apply a force equals to gravity. As a result, its position is higher, and it has more gravitational potential energy. 2. Gravitational potential energy is the energy stored in an object as the result of its height 3. The energy is stored as the result of the gravitational attraction of the Earth for the object. 4. Gravitational depends on a. mass, in kg b. acceleration due to gravity, 9. 81 m/s 2 c. height, in m

Gravitational potential energy Equation Gravitation potential energy equals to work done against gravity. change in height, Gravitational attraction between Earth and in meters the object: m: mass, in kilograms g: acceleration due to gravity = 9. 81 m/s 2

Unit of energy • The unit of energy is the same as work: Joules • 1 joule = 1 (kg)∙(m/s 2)∙(m) = 1 Newton ∙ meter • 1 joule = 1 (kg)∙(m 2/s 2) Work and energy has the same unit
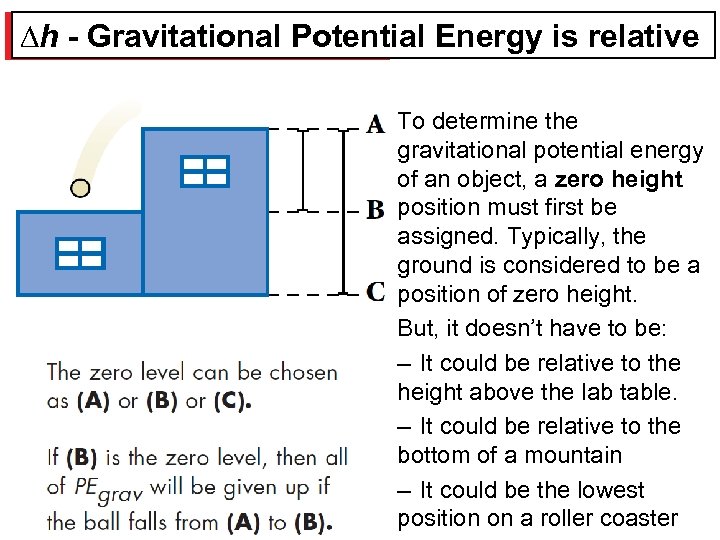
∆h - Gravitational Potential Energy is relative To determine the gravitational potential energy of an object, a zero height position must first be assigned. Typically, the ground is considered to be a position of zero height. But, it doesn’t have to be: – It could be relative to the height above the lab table. – It could be relative to the bottom of a mountain – It could be the lowest position on a roller coaster

Change in GPE only depends on change in height, not path As long as the object starts and ends at the same height, the object has the same change in GPE because gravity does the same amount of work regardless of which path is taken.

Example • The diagram shows points A, B, and C at or near Earth’s surface. As a mass is moved from A to B, 100. joules of work are done against gravity. What is the amount of work done against gravity as an identical mass is moved from A to C? 100 J As long as the object starts and ends at the same height, the object has the same change in GPE because gravity does the same amount of work regardless of which path is taken.

Work done against gravity = ∆GPE • • • How much potential energy is gained by an object with a mass of 2. 00 kg that is lifted from the floor to the top of 0. 92 m high table? Known: Solve: m = 2. 00 kg ∆PE = mg∆h h = 0. 92 m ∆PE = (2. 00 kg)(9. 81 m/s 2)(0. 92 m) = 18 J g = 9. 81 m/s 2 • unknown: • PE = ? J
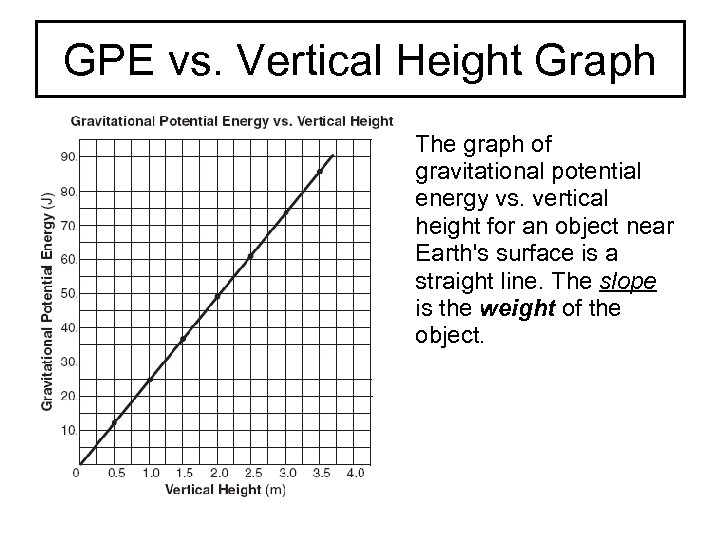
GPE vs. Vertical Height Graph The graph of gravitational potential energy vs. vertical height for an object near Earth's surface is a straight line. The slope is the weight of the object.

Elastic potential energy • Elastic potential energy is the energy stored in elastic materials as the result of their stretching or compressing when a force is applied. • Elastic potential energy can be stored in – Rubber bands – Bungee cores – Springs – trampolines
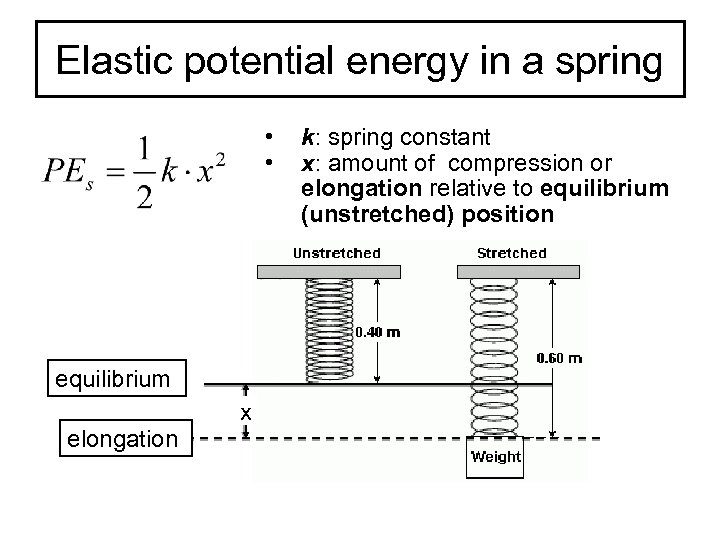
Elastic potential energy in a spring • • equilibrium x elongation k: spring constant x: amount of compression or elongation relative to equilibrium (unstretched) position
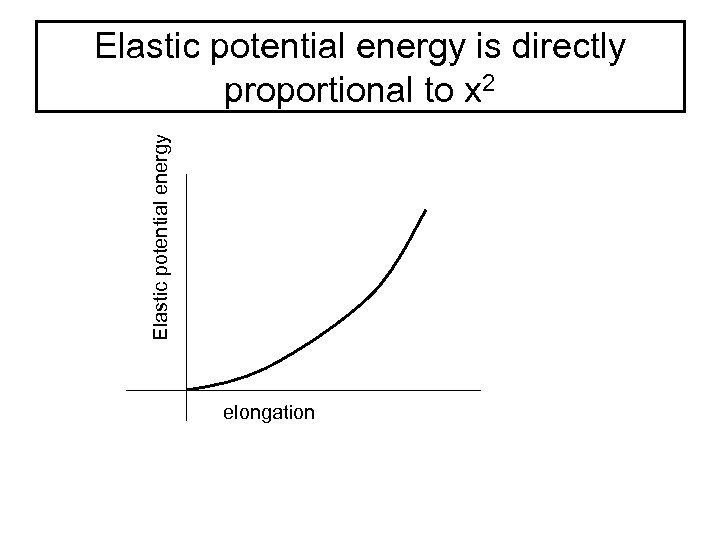
Elastic potential energy is directly proportional to x 2 elongation
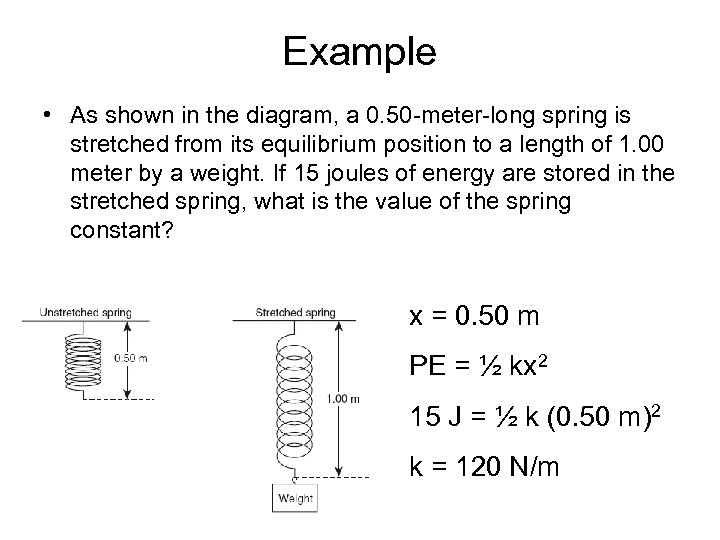
Example • As shown in the diagram, a 0. 50 -meter-long spring is stretched from its equilibrium position to a length of 1. 00 meter by a weight. If 15 joules of energy are stored in the stretched spring, what is the value of the spring constant? x = 0. 50 m PE = ½ kx 2 15 J = ½ k (0. 50 m)2 k = 120 N/m

Example • The unstretched spring in the diagram has a length of 0. 40 meter and a spring constant k. A weight is hung from the spring, causing it to stretch to a length of 0. 60 meter. In terms of k, how many joules of elastic potential energy are stored in this stretched spring? x = 0. 20 m PEs = ½ kx 2 PEs = ½ k(0. 20 m)2 PEs = (0. 020 k) J

Elongation ( or compression) depends on force • For certain springs, the amount of force (F) is directly proportional to the amount of elongation or compression (x); the constant of proportionality is known as the spring constant (k).

Hooke’s Law • F in the force needed to displace (by stretching or compressing) a spring x meters from the equilibrium (relaxed) position. The SI unit of F is Newton. • k is spring constant. It is a measure of stiffness of the spring. The greater value of k means a stiffer spring because more force is needed to stretch or compress it that spring. The SI units of k are N/m. • x the distance difference between the length of stretched/compressed spring and its relaxed (equilibrium) spring.

The slope of Fs vs. x • Spring force is directly proportional to the elongation of the spring (displacement) force The slope represents spring constant: k = F / x (N/m) elongation
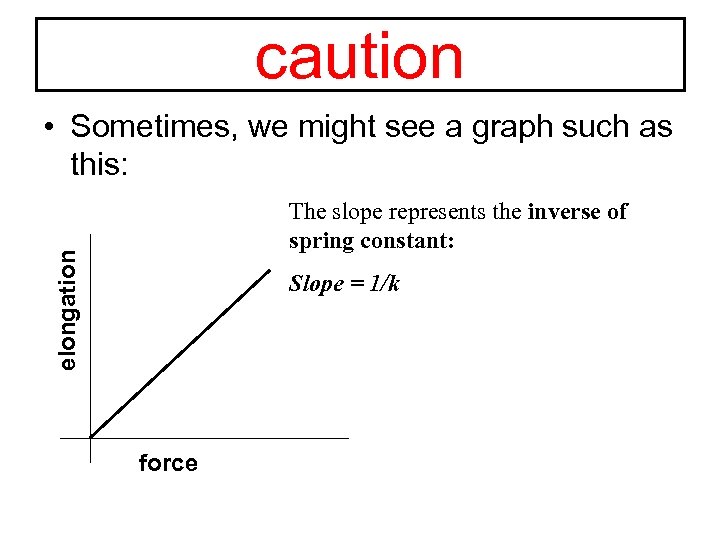
caution • Sometimes, we might see a graph such as this: elongation The slope represents the inverse of spring constant: Slope = 1/k force
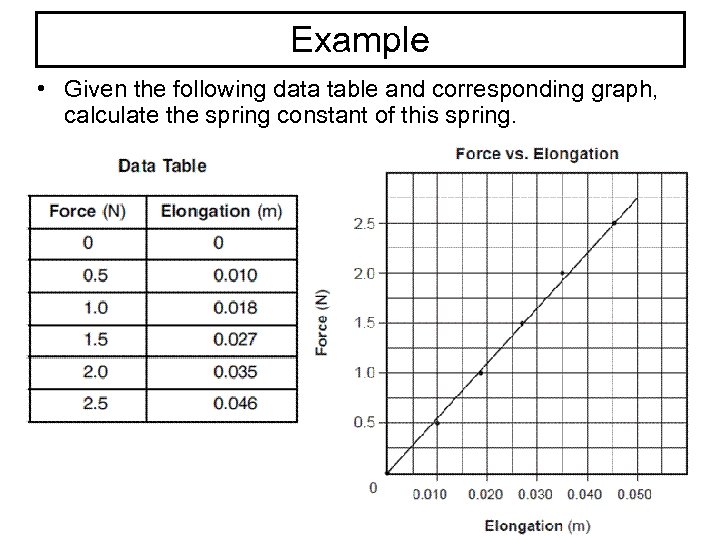
Example • Given the following data table and corresponding graph, calculate the spring constant of this spring.
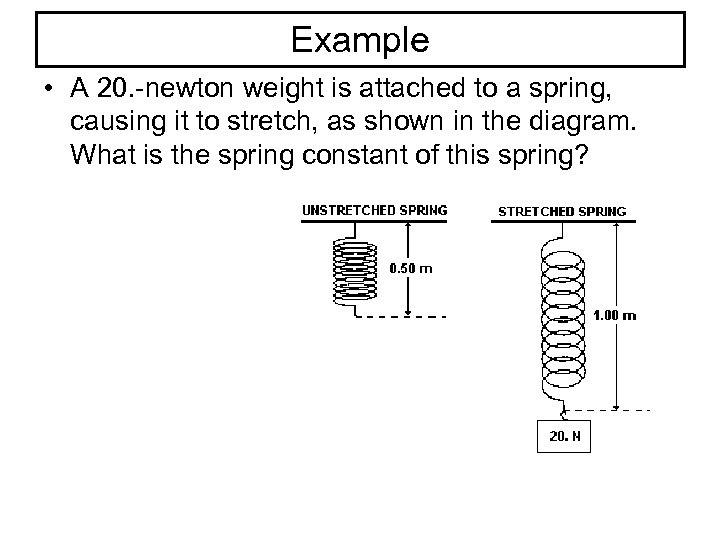
Example • A 20. -newton weight is attached to a spring, causing it to stretch, as shown in the diagram. What is the spring constant of this spring?
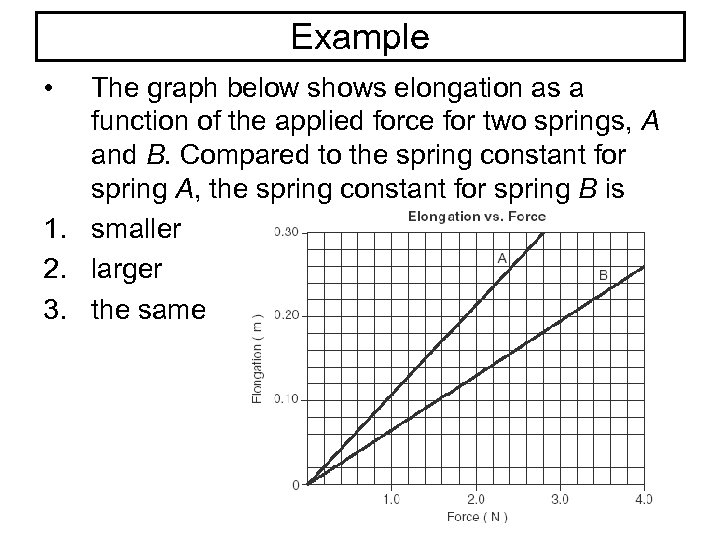
Example • The graph below shows elongation as a function of the applied force for two springs, A and B. Compared to the spring constant for spring A, the spring constant for spring B is 1. smaller 2. larger 3. the same
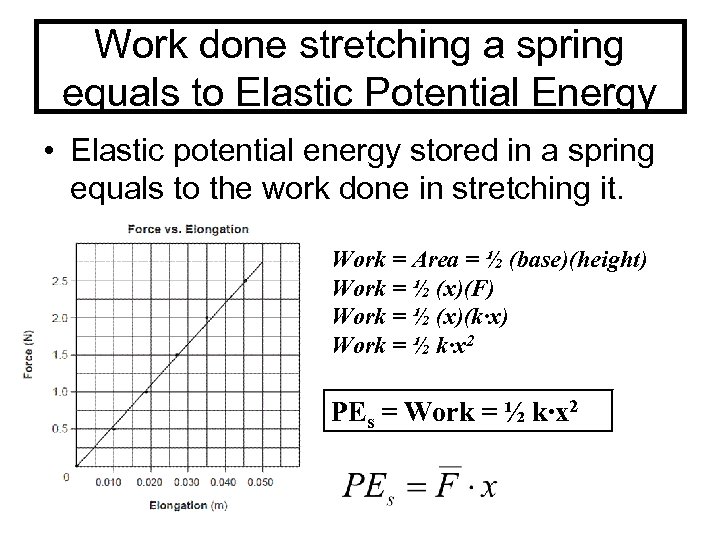
Work done stretching a spring equals to Elastic Potential Energy • Elastic potential energy stored in a spring equals to the work done in stretching it. Work = Area = ½ (base)(height) Work = ½ (x)(F) Work = ½ (x)(k∙x) Work = ½ k∙x 2 PEs = Work = ½ k∙x 2

Example • If a mass of 0. 55 kg attached to a vertical spring stretches the spring 2. 0 cm from its original equilibrium position, what is the spring constant?

Example • Determine the potential energy stored in the spring with a spring constant of 25. 0 N/m when a force of 2. 50 N is applied to it. Solve: Given: PEs = ½ k∙x 2 Fs = 2. 50 N To find x, use Fs = kx, k = 25. 0 N/m (2. 50 N) = (25. 0 N/m)(x) Unknown: x = 0. 100 m PEs = ? J PEs = ½ (25. 0 N/m)(0. 100 m)2 PEs = 0. 125 J

Example • A 10. -newton force is required to hold a stretched spring 0. 20 meter from its rest position. What is the potential energy stored in the stretched spring?

Kinetic energy • Kinetic energy is the energy of motion. • An object which has motion - whether it be vertical or horizontal motion - has kinetic energy. • The equation for kinetic energy is: KE = ½ mv 2 – Where KE is kinetic energy, in joules – v is the speed of the object, in m/s – m is the mass of the object, in kg • Like potential energy, kinetic energy is a scalar quantity.

Questions 1. Which of the following has kinetic energy? a. a falling sky diver b. a parked car c. a shark chasing a fish d. a calculator sitting on a desk 2. If a bowling ball and a volleyball are traveling at the same speed, do they have the same kinetic energy? 3. Car A and car B are identical and are traveling at the same speed. Car A is going north while car B is going east. Which car has greater kinetic energy?
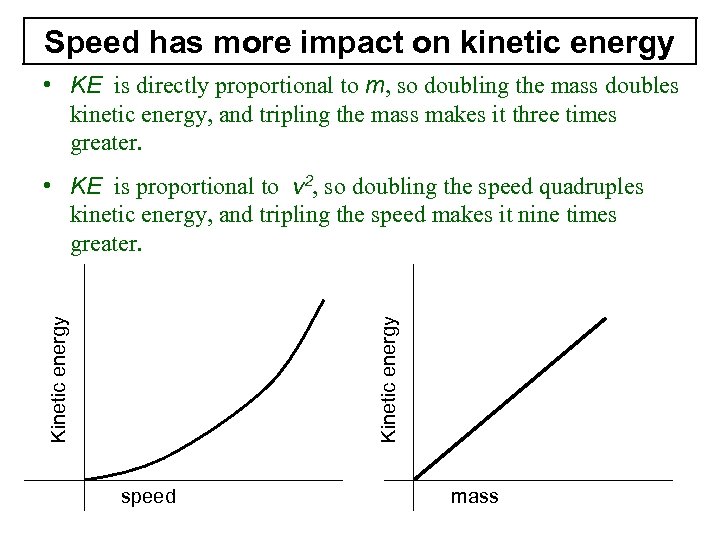
Speed has more impact on kinetic energy • KE is directly proportional to m, so doubling the mass doubles kinetic energy, and tripling the mass makes it three times greater. Kinetic energy • KE is proportional to v 2, so doubling the speed quadruples kinetic energy, and tripling the speed makes it nine times greater. speed mass

Example • A 7. 00 kg bowling ball moves at 3. 00 m/s. How much kinetic energy does the bowling ball heave? How fast must a 2. 45 g tabletennis ball move in order to have the same kinetic energy as the bowling ball? Is this speed reasonable for a table-tennis ball?

Example • An object moving at a constant speed of 25 meters per second possesses 450 joules of kinetic energy. What is the object's mass? Known: • KE = 450 J • v = 25 m/s Unknown: • m = ? kg Solve: KE = ½ mv 2 450 J = ½ (m)(25 m/s)2 m = 1. 4 kg

Example • a. b. c. d. A cart of mass m traveling at a speed v has kinetic energy KE. If the mass of the cart is doubled and its speed is halved, the kinetic energy of the cart will be half as great twice as great one-fourth as great four times as great
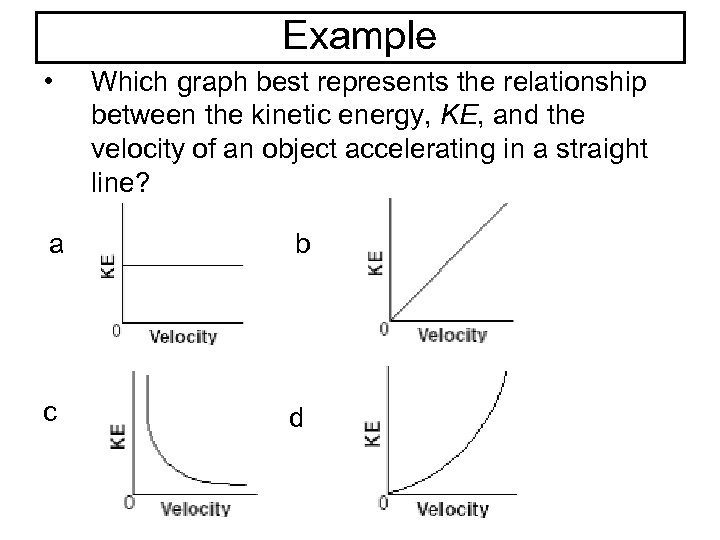
Example • Which graph best represents the relationship between the kinetic energy, KE, and the velocity of an object accelerating in a straight line? a b c d

Total Mechanical Energy • Mechanical energy is the energy that is possessed by an object due to its motion or due to its position. Mechanical energy can be either kinetic energy (energy of motion) or potential energy (stored energy of position) or both. The total amount of mechanical energy is merely the sum of the potential energy and the kinetic energy TME = KE + PE TME = PEgrav + PEspring + KE Note: PE includes both gravitational potential energy and elastic potential energy.

Mechanical Energy as the Ability to Do Work • Any object that possesses mechanical energy - whether it is in the form of potential energy or kinetic energy - is able to do work.

Internal Energy • internal energy: TEMPERATURE/HEAT Resistance force, such as friction, air resistance, or any force stopping motion, produce internal energy. When resistance force is zero, internal energy does not change.
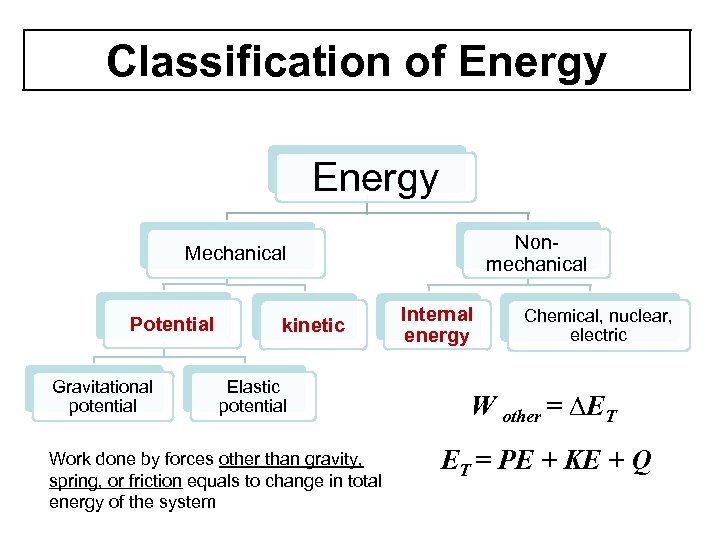
Classification of Energy Nonmechanical Mechanical Potential Gravitational potential kinetic Elastic potential Work done by forces other than gravity, spring, or friction equals to change in total energy of the system Internal energy Chemical, nuclear, electric W other = ∆ET ET = PE + KE + Q
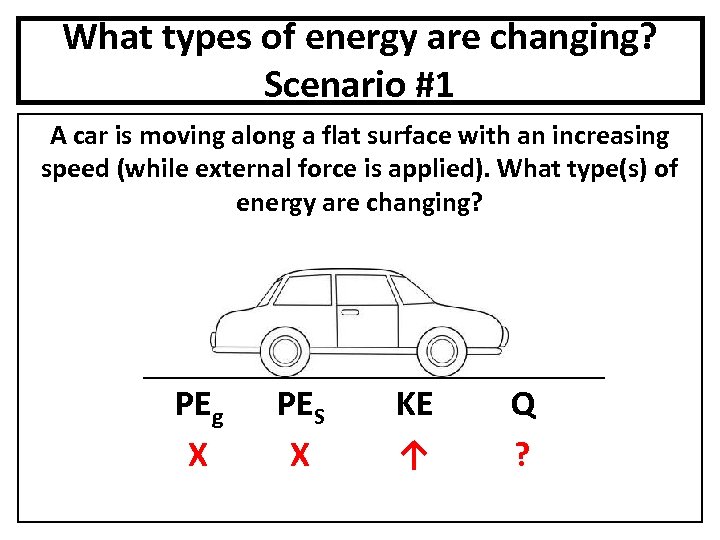
What types of energy are changing? Scenario #1 A car is moving along a flat surface with an increasing speed (while external force is applied). What type(s) of energy are changing? PEg X PES X KE ↑ Q ?
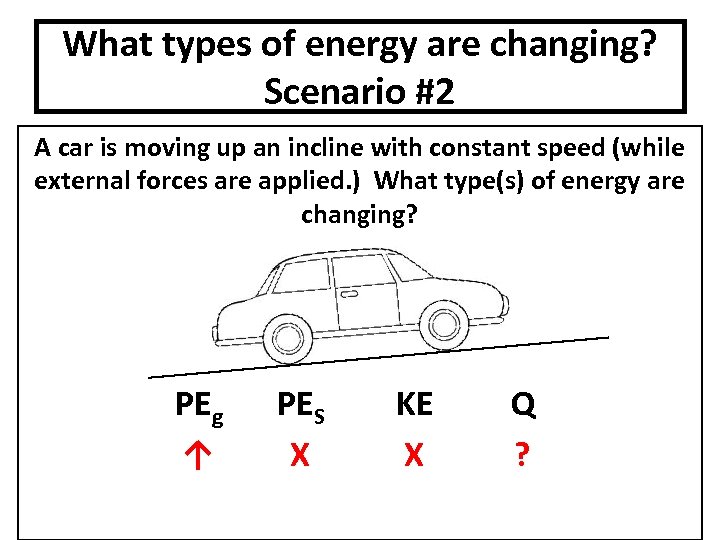
What types of energy are changing? Scenario #2 A car is moving up an incline with constant speed (while external forces are applied. ) What type(s) of energy are changing? PEg ↑ PES X KE X Q ?
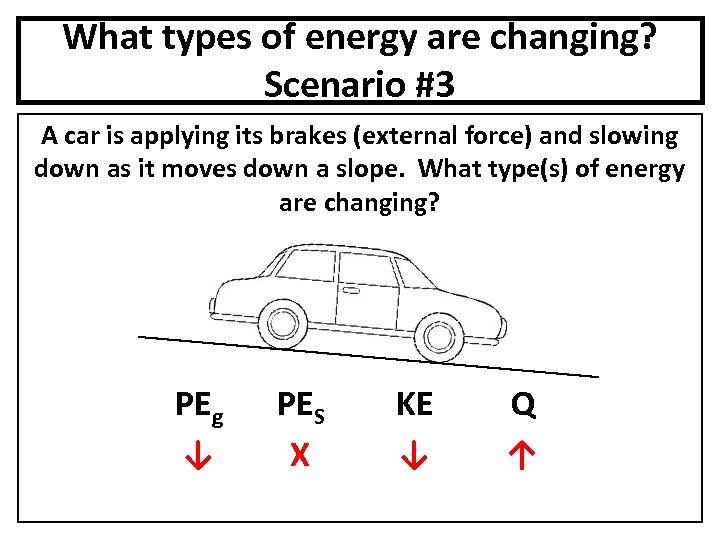
What types of energy are changing? Scenario #3 A car is applying its brakes (external force) and slowing down as it moves down a slope. What type(s) of energy are changing? PEg ↓ PES X KE ↓ Q ↑
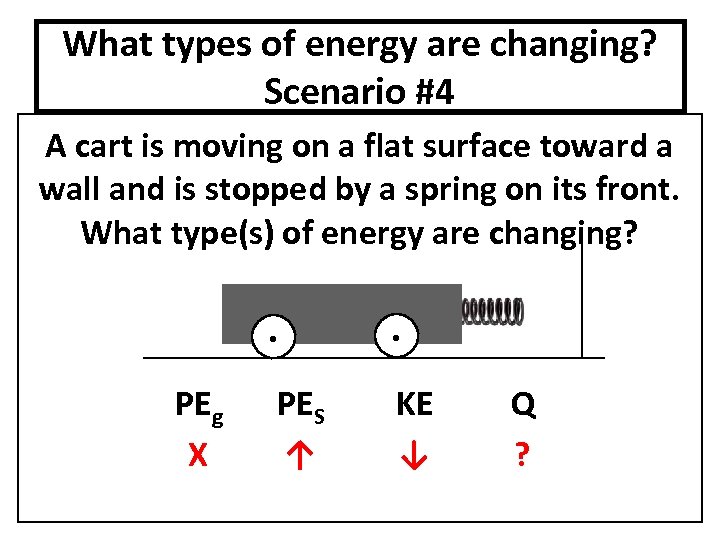
What types of energy are changing? Scenario #4 A cart is moving on a flat surface toward a wall and is stopped by a spring on its front. What type(s) of energy are changing? PEg X PES ↑ KE ↓ Q ?
What types of energy are changing? Scenario #5 A rocket flies upward with an increasing velocity [ignore air resistance]. What type(s) of energy are changing? PEg ↑ PES X KE ↑ Q X

Lesson 2: The Work-Energy Theorem • • • Work and Energy principle Analysis of Situations Involving external forces Analysis of Situations Involving a closed system Analysis of Situations Involving an ideal system Application and Practice Questions
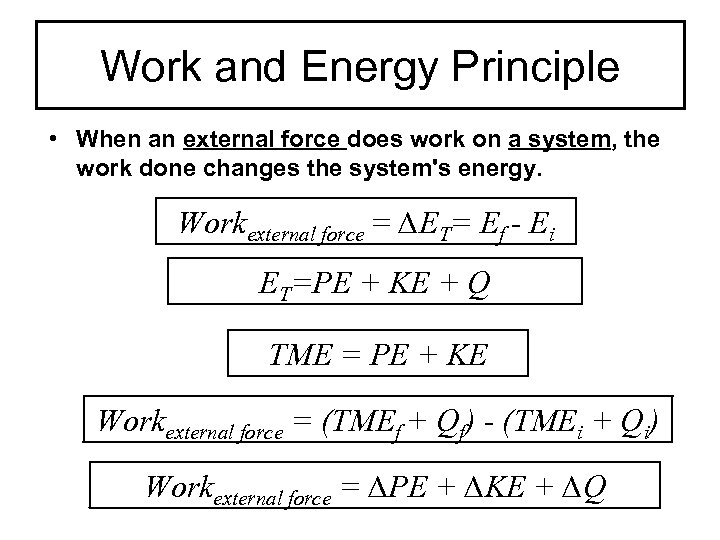
Work and Energy Principle • When an external force does work on a system, the work done changes the system's energy. Workexternal force = ∆ET= Ef - Ei ET=PE + KE + Q TME = PE + KE Workexternal force = (TMEf + Qf) - (TMEi + Qi) Workexternal force = ∆PE + ∆KE + ∆Q

What is a system? And what are internal, external forces? • Any sets of objects can be considered A SYSTEM. The definition of system can be arbitrary. However, according to New York State Regents Physics, examples of a system are apple and Earth, two cars in a collision, two cars connected by a spring, rifle and bullets, cannon and cannon ball, spring and its launched toy, car and road. • The forces within a system are called internal forces. Example of internal forces include gravity (between apple and Earth), force by the spring between two connected cars, force of friction between car and road. • Applied force to a system is an example external force
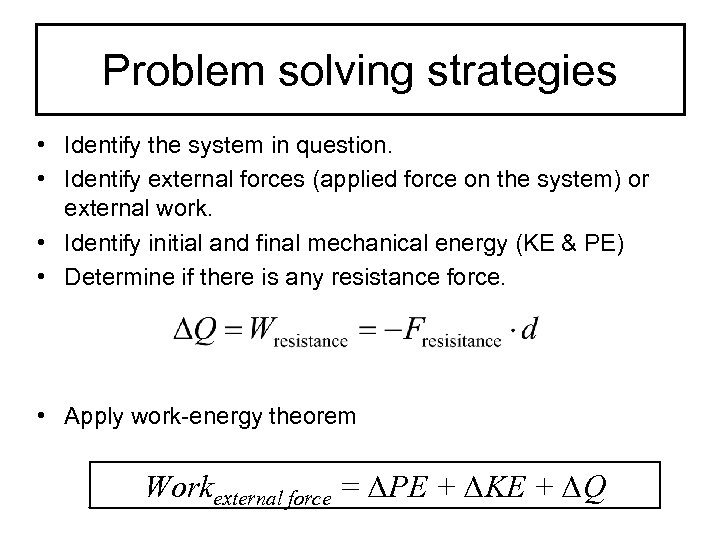
Problem solving strategies • Identify the system in question. • Identify external forces (applied force on the system) or external work. • Identify initial and final mechanical energy (KE & PE) • Determine if there is any resistance force. • Apply work-energy theorem Workexternal force = ∆PE + ∆KE + ∆Q
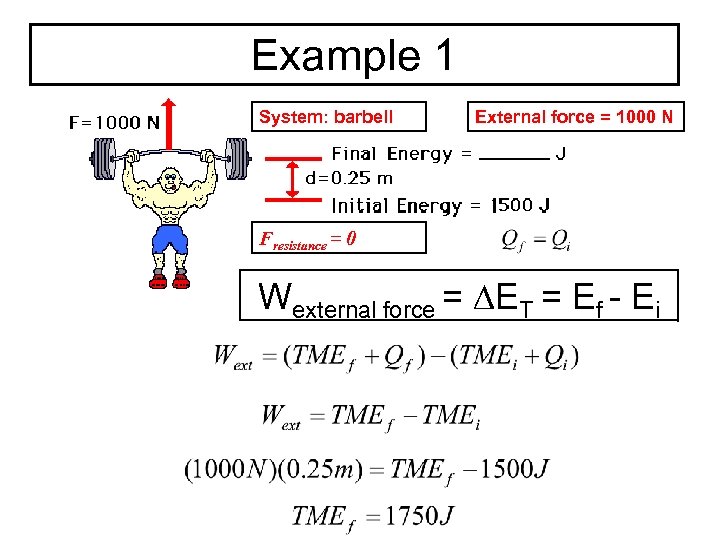
Example 1 System: barbell External force = 1000 N Fresistance = 0 Wexternal force = ∆ET = Ef - Ei
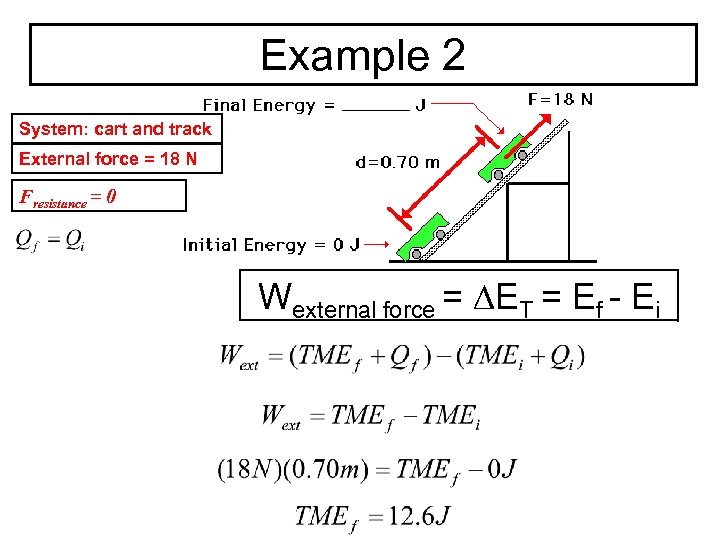
Example 2 System: cart and track External force = 18 N Fresistance = 0 Wexternal force = ∆ET = Ef - Ei

Example 3 • A person does 100 joules of work in pulling back the string of a bow. What will be the initial speed of a 0. 5 -kilogram arrow when it is fired from the bow? System: bow External work = 100 J Fresistance = 0

ENERGY IS CONSERVED IN A CLOSED SYSTEM • A closed system is one in which there are no external forces doing work on the system, no external work being done by the system, an no transfer of energy into or out of the system. • Although the energy within a closed system may be transformed from one type to anther, the total amount of energy in a closed system must remain constant – energy is never created or destroyed. Wext = ∆ET = 0
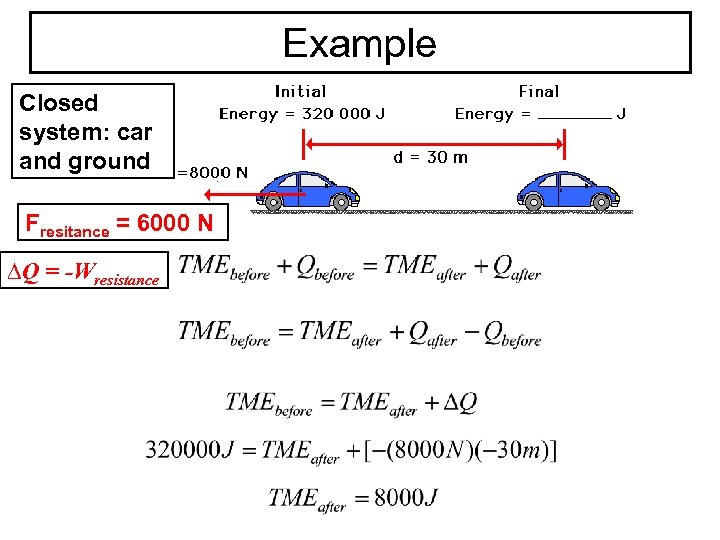
Example Closed system: car and ground Fresitance = 6000 N ∆Q = -Wresistance
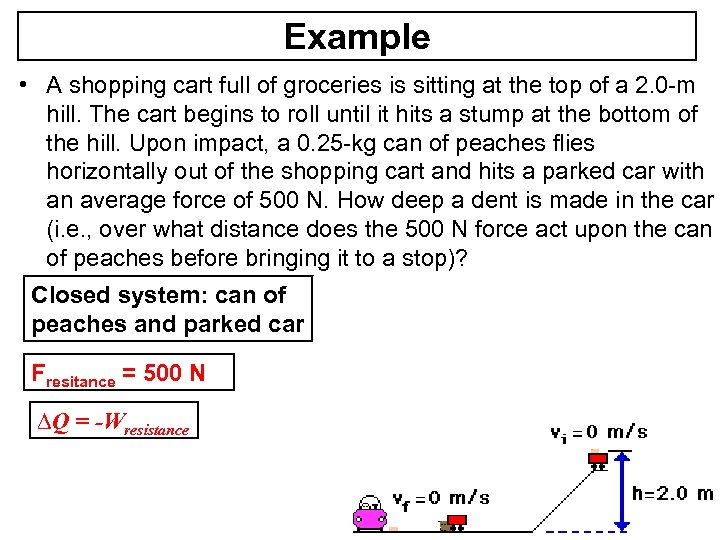
Example • A shopping cart full of groceries is sitting at the top of a 2. 0 -m hill. The cart begins to roll until it hits a stump at the bottom of the hill. Upon impact, a 0. 25 -kg can of peaches flies horizontally out of the shopping cart and hits a parked car with an average force of 500 N. How deep a dent is made in the car (i. e. , over what distance does the 500 N force act upon the can of peaches before bringing it to a stop)? Closed system: can of peaches and parked car Fresitance = 500 N ∆Q = -Wresistance
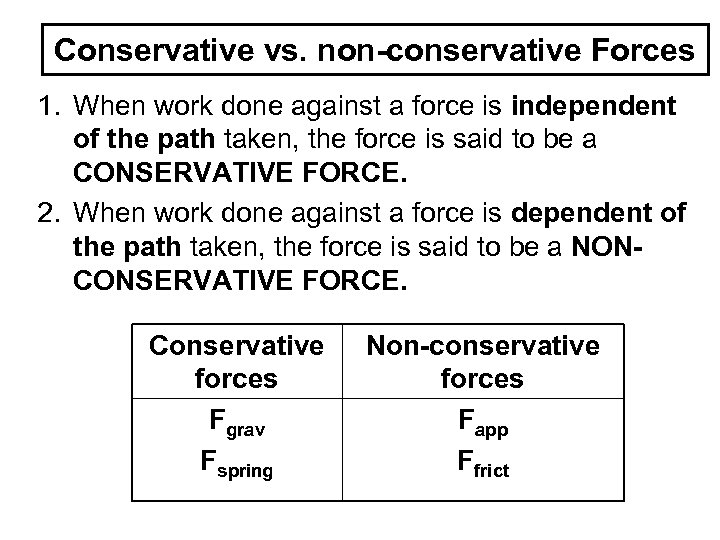
Conservative vs. non-conservative Forces 1. When work done against a force is independent of the path taken, the force is said to be a CONSERVATIVE FORCE. 2. When work done against a force is dependent of the path taken, the force is said to be a NONCONSERVATIVE FORCE. Conservative forces Fgrav Fspring Non-conservative forces Fapp Ffrict

Ideal Mechanical System • An ideal mechanical system is a closed system in which no friction or other non-conservative force acts. The only forces doing work are gravity, or force of a spring. • In an ideal mechanical system total mechanical energy remains the same: Wext = ∆ET = 0
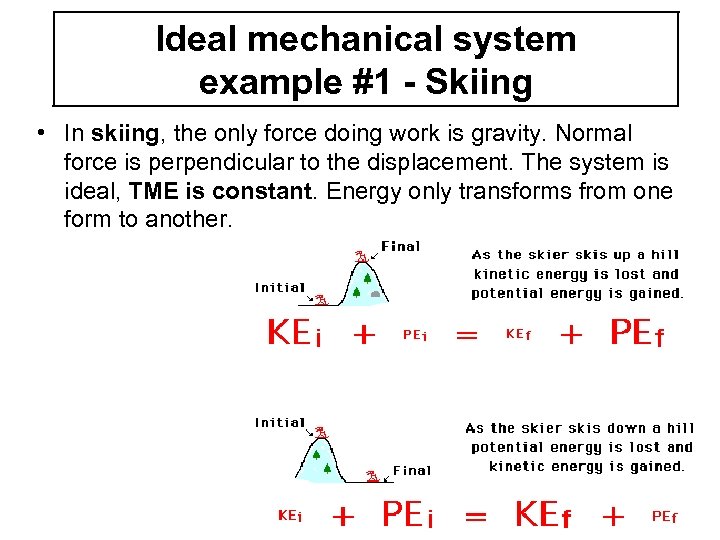
Ideal mechanical system example #1 - Skiing • In skiing, the only force doing work is gravity. Normal force is perpendicular to the displacement. The system is ideal, TME is constant. Energy only transforms from one form to another.
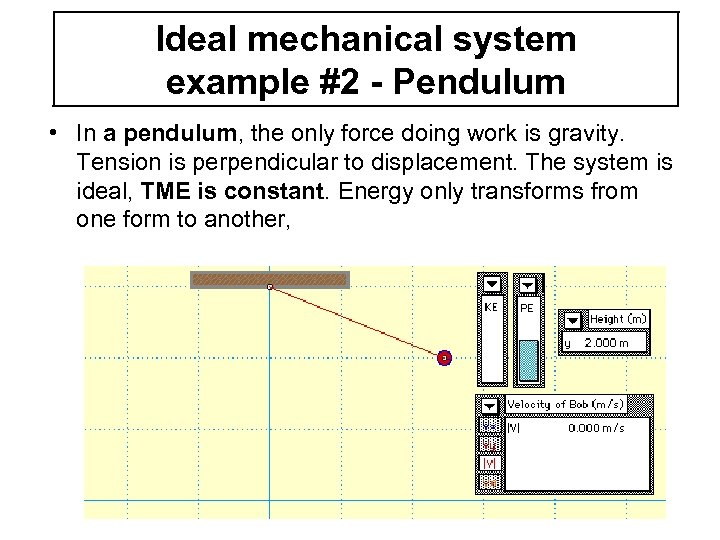
Ideal mechanical system example #2 - Pendulum • In a pendulum, the only force doing work is gravity. Tension is perpendicular to displacement. The system is ideal, TME is constant. Energy only transforms from one form to another,
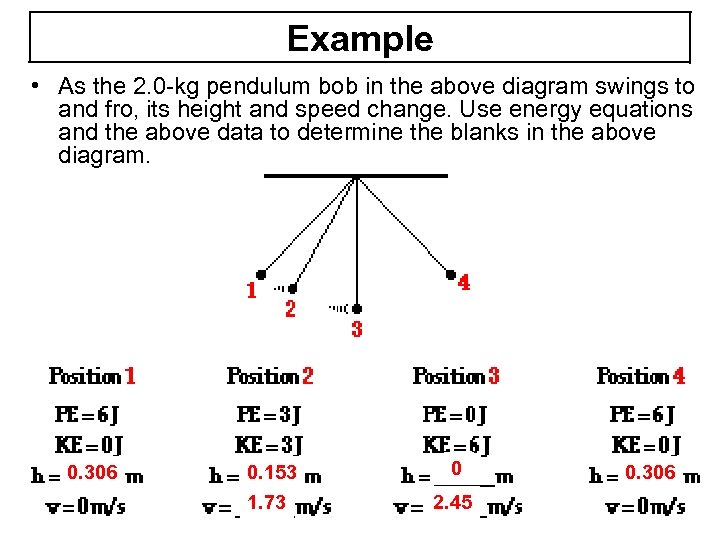
Example • As the 2. 0 -kg pendulum bob in the above diagram swings to and fro, its height and speed change. Use energy equations and the above data to determine the blanks in the above diagram. 0. 306 0. 153 1. 73 0 2. 45 0. 306

Example • 1. 2. 3. 4. As the pendulum swings from position A to position C as shown in the diagram, what is the relationship of kinetic energy to potential energy? [Neglect friction. ] The kinetic energy decreases more than the potential energy increases. The kinetic energy increases more than the potential energy decreases. The kinetic energy decrease is equal to the potential energy increase. The kinetic energy increase is equal to the potential energy decrease.
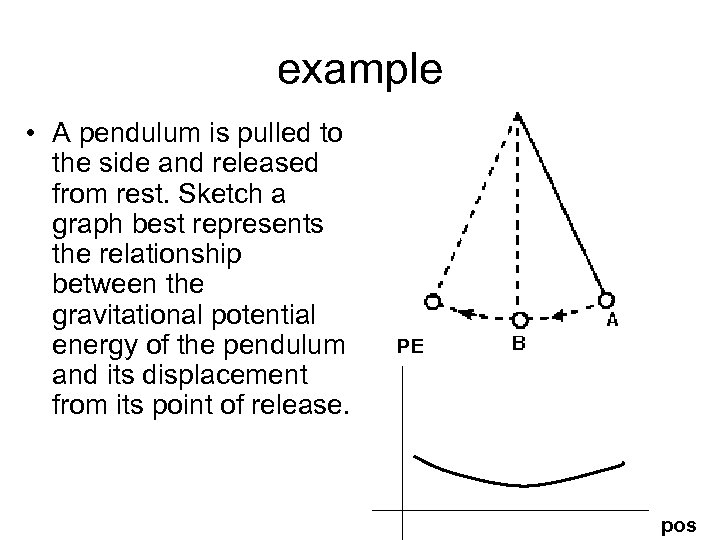
example • A pendulum is pulled to the side and released from rest. Sketch a graph best represents the relationship between the gravitational potential energy of the pendulum and its displacement from its point of release. PE pos
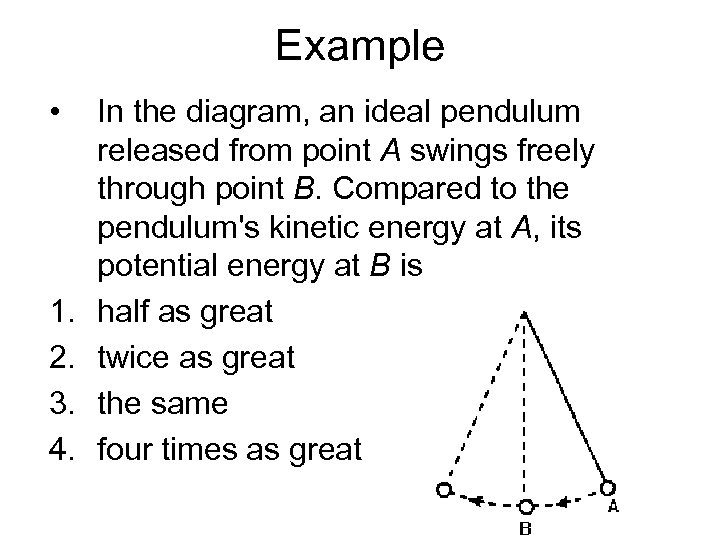
Example • 1. 2. 3. 4. In the diagram, an ideal pendulum released from point A swings freely through point B. Compared to the pendulum's kinetic energy at A, its potential energy at B is half as great twice as great the same four times as great
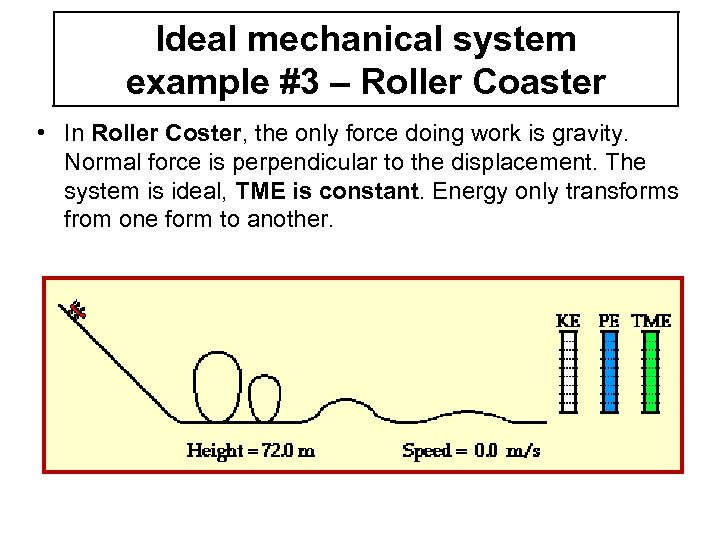
Ideal mechanical system example #3 – Roller Coaster • In Roller Coster, the only force doing work is gravity. Normal force is perpendicular to the displacement. The system is ideal, TME is constant. Energy only transforms from one form to another.
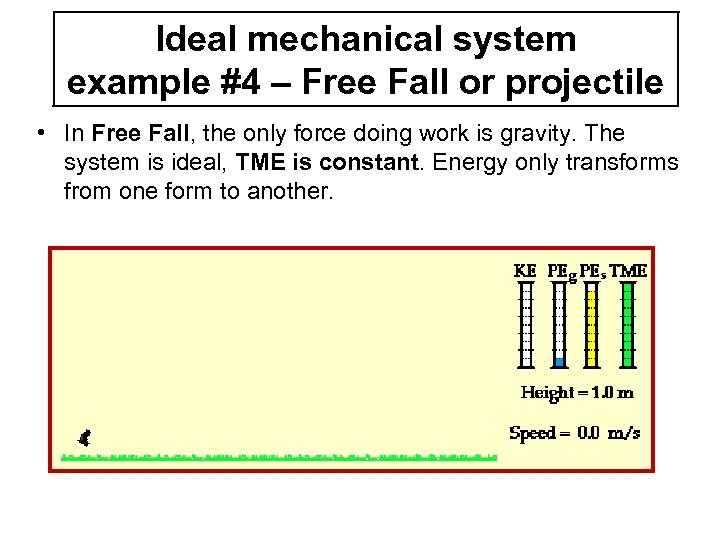
Ideal mechanical system example #4 – Free Fall or projectile • In Free Fall, the only force doing work is gravity. The system is ideal, TME is constant. Energy only transforms from one form to another.
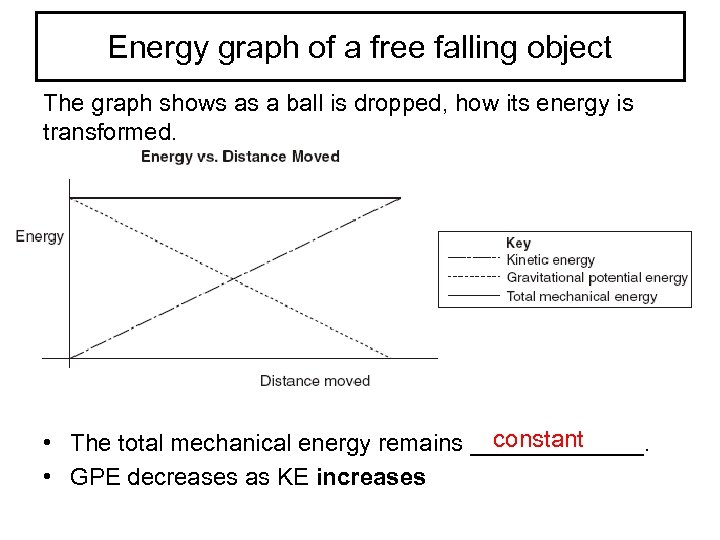
Energy graph of a free falling object The graph shows as a ball is dropped, how its energy is transformed. constant • The total mechanical energy remains _______. • GPE decreases as KE increases
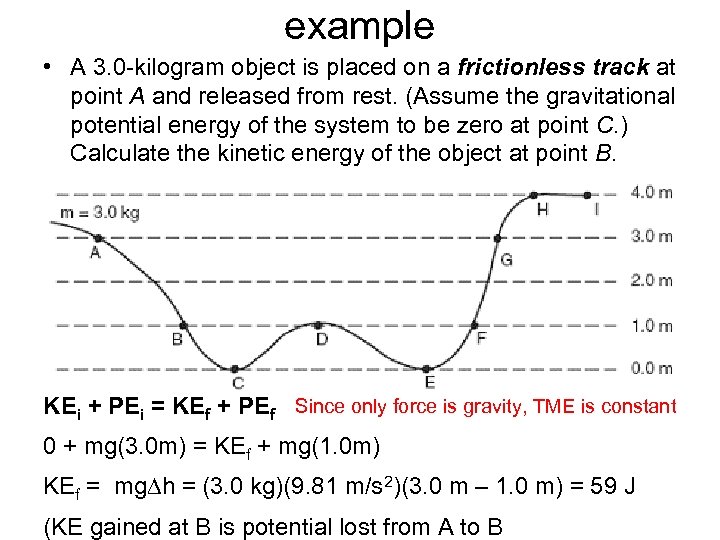
example • A 3. 0 -kilogram object is placed on a frictionless track at point A and released from rest. (Assume the gravitational potential energy of the system to be zero at point C. ) Calculate the kinetic energy of the object at point B. KEi + PEi = KEf + PEf Since only force is gravity, TME is constant 0 + mg(3. 0 m) = KEf + mg(1. 0 m) KEf = mg∆h = (3. 0 kg)(9. 81 m/s 2)(3. 0 m – 1. 0 m) = 59 J (KE gained at B is potential lost from A to B
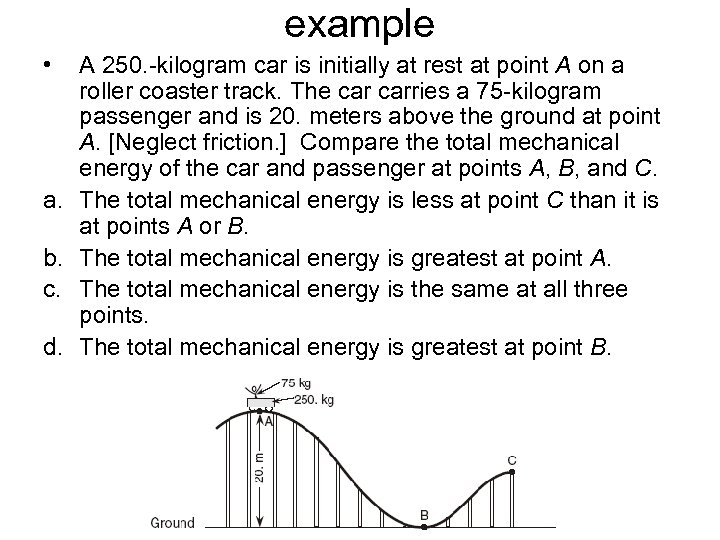
example • a. b. c. d. A 250. -kilogram car is initially at rest at point A on a roller coaster track. The carries a 75 -kilogram passenger and is 20. meters above the ground at point A. [Neglect friction. ] Compare the total mechanical energy of the car and passenger at points A, B, and C. The total mechanical energy is less at point C than it is at points A or B. The total mechanical energy is greatest at point A. The total mechanical energy is the same at all three points. The total mechanical energy is greatest at point B.
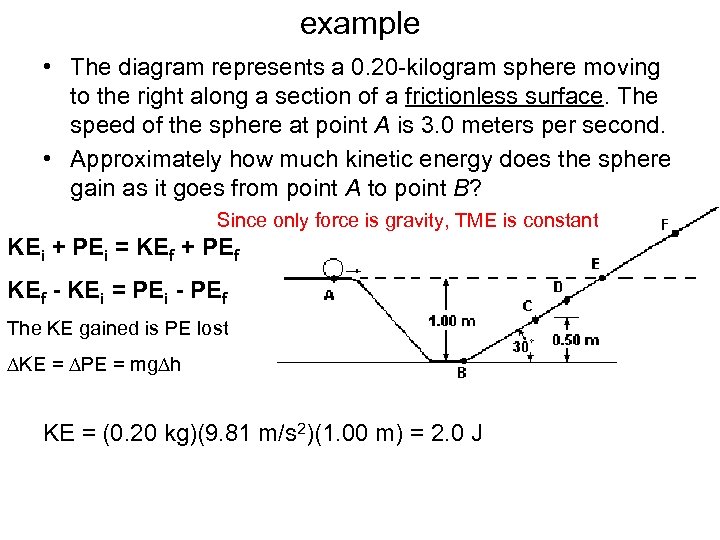
example • The diagram represents a 0. 20 -kilogram sphere moving to the right along a section of a frictionless surface. The speed of the sphere at point A is 3. 0 meters per second. • Approximately how much kinetic energy does the sphere gain as it goes from point A to point B? Since only force is gravity, TME is constant KEi + PEi = KEf + PEf KEf - KEi = PEi - PEf The KE gained is PE lost ∆KE = ∆PE = mg∆h KE = (0. 20 kg)(9. 81 m/s 2)(1. 00 m) = 2. 0 J

example • A 1. 0 kg mass falls freely for 20. meters near the surface of Earth. What is the total KE gained by the object during its free fall? Since only force is gravity, TME is constant KEi + PEi = KEf + PEf KEf - KEi = PEi - PEf ∆KE (gained) = GPE (lost) ∆KE = (1. 0 kg)(9. 81 m/s 2)(20. m-0) = 2. 0 x 102 J

Ideal mechanical system example #5 – Pop Up toy • In Pop Up toy, the only force doing work is gravity and force on a spring. The system is ideal, TME is constant. Energy only transforms from one form to another. Initially, at the bottom: TMEi = ½ kx 2 Finally, at the top: TMEf = mgh TMEf = TMEi ½ kx 2 = mgh

Work and Energy Thorem 1. When external force does work on a system, its total energy is changed. 2. When external force is zero, the system is closed, its total energy is conserved. 3. In a closed system, if the only force doing work are conservative forces (no friction), the total mechanical energy is conserved.
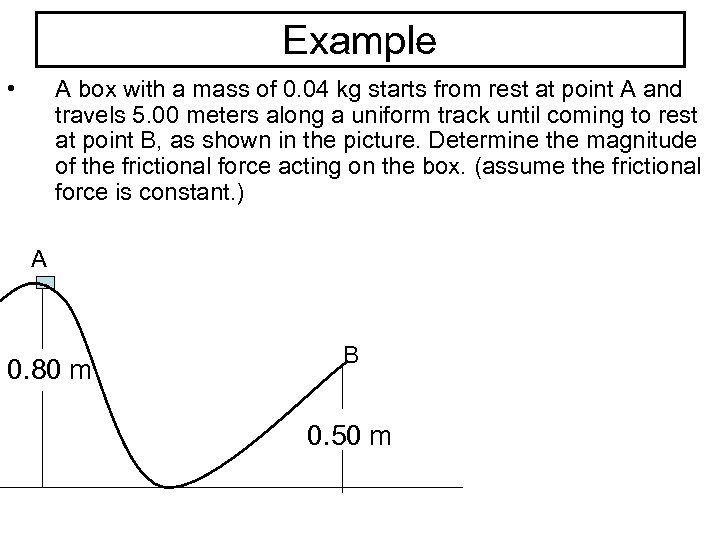
Example • A box with a mass of 0. 04 kg starts from rest at point A and travels 5. 00 meters along a uniform track until coming to rest at point B, as shown in the picture. Determine the magnitude of the frictional force acting on the box. (assume the frictional force is constant. ) A 0. 80 m B 0. 50 m
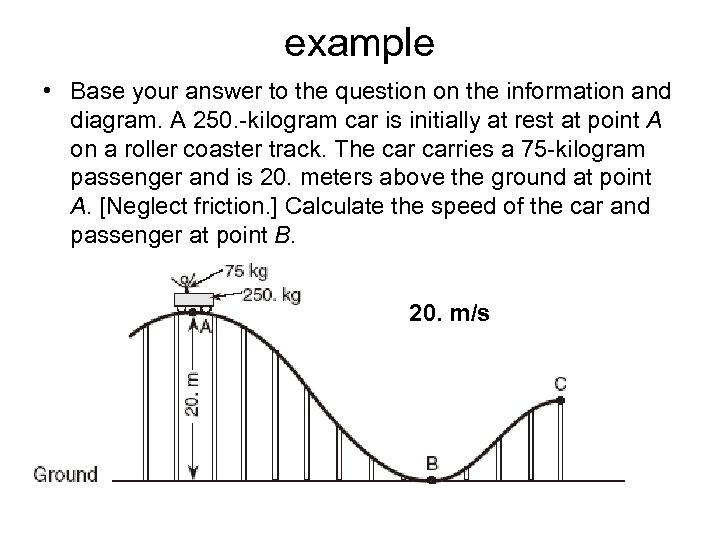
example • Base your answer to the question on the information and diagram. A 250. -kilogram car is initially at rest at point A on a roller coaster track. The carries a 75 -kilogram passenger and is 20. meters above the ground at point A. [Neglect friction. ] Calculate the speed of the car and passenger at point B. 20. m/s
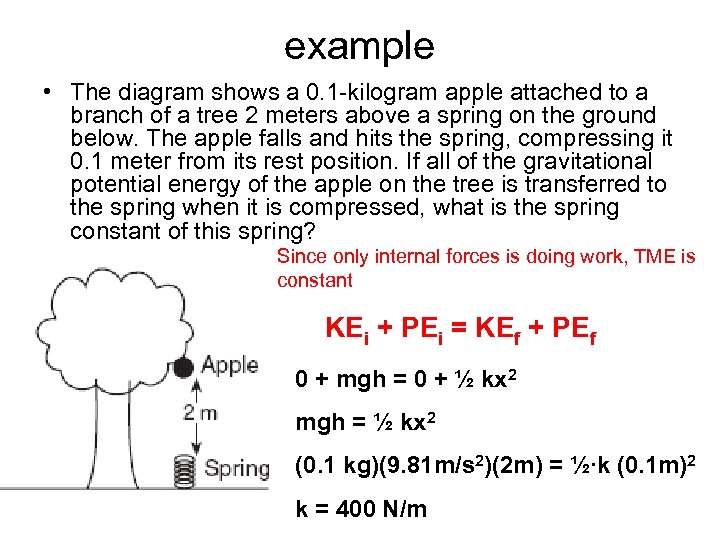
example • The diagram shows a 0. 1 -kilogram apple attached to a branch of a tree 2 meters above a spring on the ground below. The apple falls and hits the spring, compressing it 0. 1 meter from its rest position. If all of the gravitational potential energy of the apple on the tree is transferred to the spring when it is compressed, what is the spring constant of this spring? Since only internal forces is doing work, TME is constant KEi + PEi = KEf + PEf 0 + mgh = 0 + ½ kx 2 mgh = ½ kx 2 (0. 1 kg)(9. 81 m/s 2)(2 m) = ½∙k (0. 1 m)2 k = 400 N/m
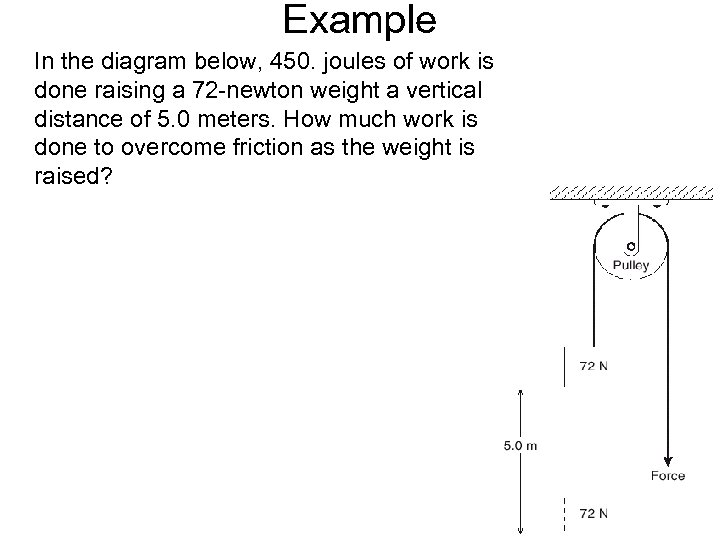
Example In the diagram below, 450. joules of work is done raising a 72 -newton weight a vertical distance of 5. 0 meters. How much work is done to overcome friction as the weight is raised?

Lab 15 – Power Purpose: To determine my power requirement for climbing a staircase - both by walking and by running. Compare the two results. Material: stop watch, ruler. Data section: should contain colomns of measured and calculated data for both walking and running up a flight of stairs. The rows and columns should be labeled; units should be identified. Work should be shown for each calculation; the work should be labeled and easy to follow. Conclusion/discussion of results: The Conclusion should (as always) answer the questions posed in the Purpose.
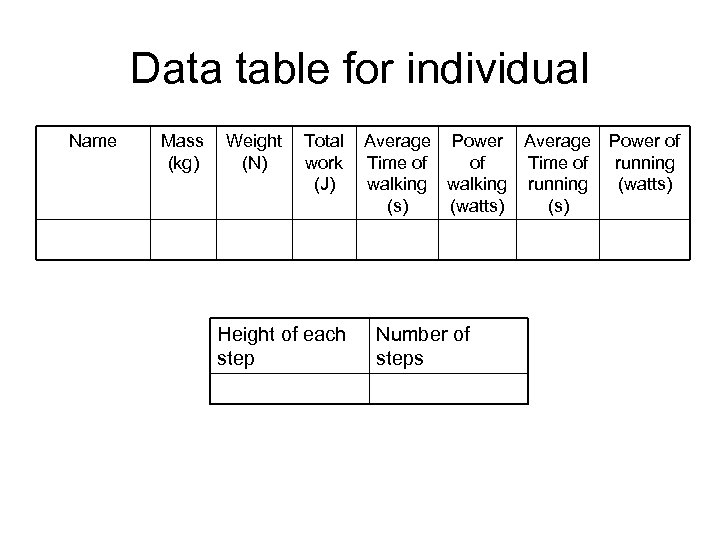
Data table for individual Name Mass Weight Total Average Power of (kg) (N) work Time of of Time of running (J) walking running (watts) (s) Height of each step Number of steps
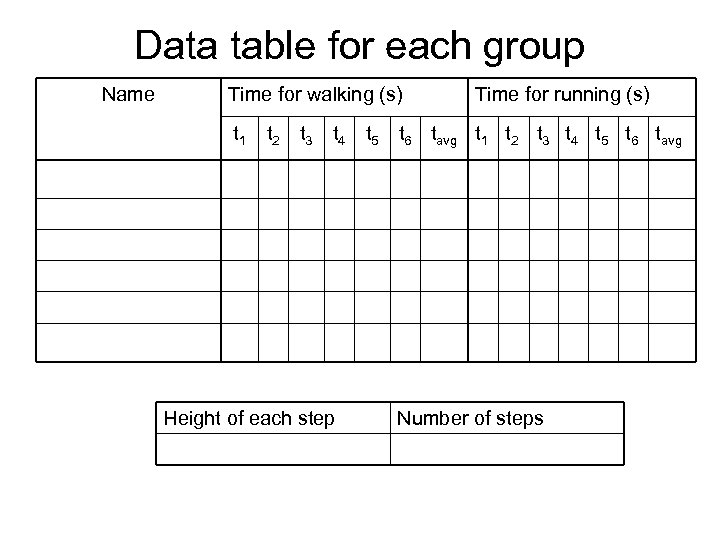
Data table for each group Name Time for walking (s) t 1 t 2 t 3 t 4 Height of each step t 5 Time for running (s) t 6 tavg t 1 t 2 t 3 t 4 t 5 t 6 tavg Number of steps

Lab 16 - Energy of a Tossed Ball OBJECTIVES 1. Measure the change in the kinetic and potential energies as a ball moves in free fall. 2. See how the total energy of the ball changes during free fall. MATERIALS computer Vernier computer interface Vernier Motion Detector ball Logger Pro wire basket

PRELIMINARY QUESTIONS • For each question, consider the free-fall portion of the motion of a ball tossed straight upward, starting just as the ball is released to just before it is caught. Assume that there is very little air resistance. 1. What form or forms of energy does the ball have while momentarily at rest at the top of the path? 2. What form or forms of energy does the ball have while in motion near the bottom of the path? 3. Sketch a graph of postion vs. time for the ball. 4. Sketch a graph of velocity vs. time for the ball. 5. Sketch a graph of kinetic energy vs. time for the ball. 6. Sketch a graph of potential energy vs. time for the ball. 7. Sketch a graph of total energy vs. time for the ball. 8. If there are no frictional forces acting on the ball, how is the change in the ball’s potential energy related to the change in kinetic energy?
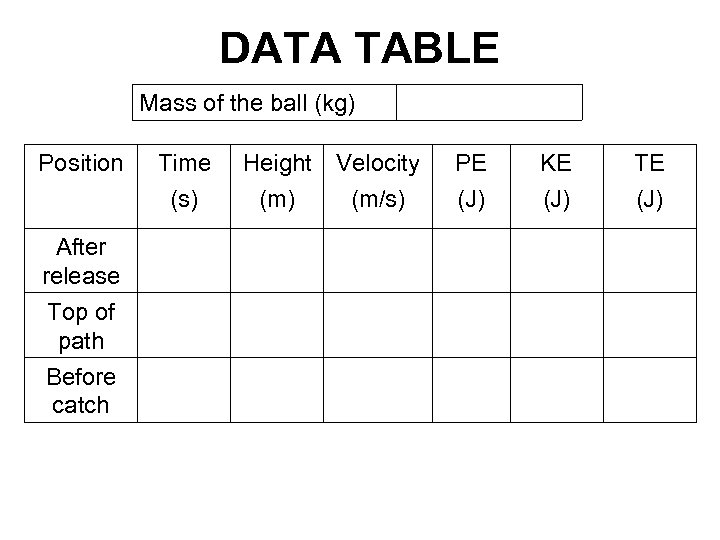
DATA TABLE Mass of the ball (kg) Position Time (s) After release Top of path Before catch Height Velocity (m) (m/s) PE KE TE (J) (J)

ANALYSIS 1. Inspect kinetic energy vs. time graph for the toss of the ball. 2. Inspect potential energy vs. time graph for the free-fall flight of the ball. 3. Inspect Total energy vs. time graph for the free-fall flight of the ball. 4. Your conclusion from this lab 1. How does the kinetic and potential energy change? 2. How does the total energy change?

Lab 14 – Hooke’s Law (1) 1. 2. 3. 4. 5. Purpose: To determine the spring constant of a given spring. Material: spring, masses, meter stick. Procedure: Hook different masses on the spring, record the force Fs (mg) and corresponding elongation x. Plot the graph of Force vs. elongation Data section: should contain colomns: force applied, elongation. – Data measured directly from the experiment. The units of measurements in a data table should be specified in column heading only. Data analysis: Graph force vs. elongation on graph paper, answer following questions: – What does the slope mean in Force vs. elongation graph? – Determine the spring constant
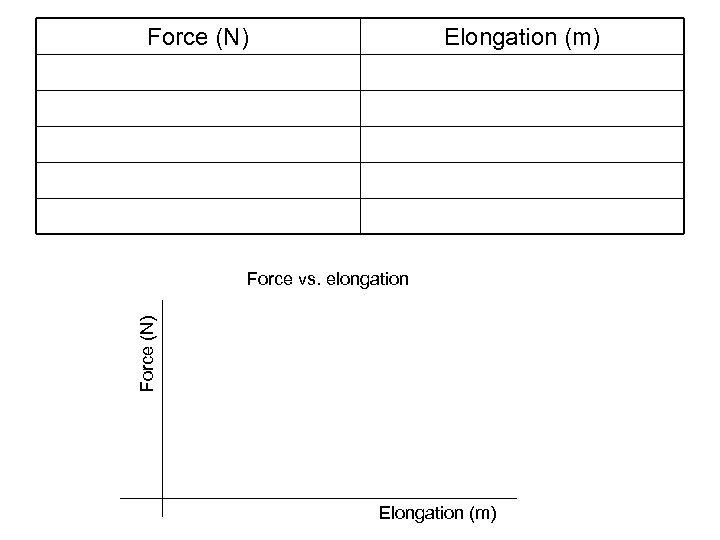
Force (N) Elongation (m) Force (N) Force vs. elongation Elongation (m)

Do now • A 1. 2 -kilogram block and a 1. 8 -kilogram block are initially at rest on a frictionless, horizontal surface. When a compressed spring between the blocks is released, the 1. 8 -kilogram block moves to the right at 2. 0 meters per second, as shown. • What is the speed of the 1. 2 -kilogram block after the spring is released?
318a43578b4aefd6e2bdf9dc5f4dee16.ppt