Work and Energy An Introduction Introduction to

Work and Energy An Introduction

Introduction to Work

Work ¢ ¢ ¢ Work tells us how much a force or combination of forces changes the energy of a system. Work is the bridge between force (a vector) and energy (a scalar). W = F r cos l l l F: force (N) r : displacement (m) : angle between force and displacement

Units of Work ¢ SI System: Joule (N m) l ¢ ¢ ¢ 1 Joule of work is done when 1 N acts on a body moving it a distance of 1 meter British System: foot-pound cgs System: erg (dyne-cm) Atomic Level: electron-Volt (e. V)

Force and direction of motion both matter in defining work! ¢ ¢ There is no work done by a force if it causes no displacement. Forces can do positive, negative, or zero work. When an box is pushed on a flat floor, for example… l l l The normal force and gravity do no work, since they are perpendicular to the direction of motion. The person pushing the box does positive work, since she is pushing in the direction of motion. Friction does negative work, since it points opposite the direction of motion.

Question ¢ If a man holds a 50 kg box at arms length for 2 hours as he stands still, how much work does he do on the box?

Question ¢ If a man holds a 50 kg box at arms length for 2 hours as he walks 1 km forward, how much work does he do on the box?

Question ¢ If a man lifts a 50 kg box 2. 0 meters, how much work does he do on the box?

Work and Energy ¢ ¢ Work changes mechanical energy! If an applied force does positive work on a system, it tries to increase mechanical energy. If an applied force does negative work, it tries to decrease mechanical energy. The two forms of mechanical energy are called potential and kinetic energy.

Sample problem Jane uses a vine wrapped around a pulley to lift a 70 -kg Tarzan to a tree house 9. 0 meters above the ground. a)How much work does Jane do when she lifts Tarzan? b)How much work does gravity do when Jane lifts Tarzan?

Sample problem Joe pushes a 10 -kg box and slides it across the floor at constant velocity of 3. 0 m/s. The coefficient of kinetic friction between the box and floor is 0. 50. a) How much work does Joe do if he pushes the box for 15 meters? b) How much work does friction do as Joe pushes the box?

Sample problem A father pulls his child in a little red wagon with constant speed. If the father pulls with a force of 16 N for 10. 0 m, and the handle of the wagon is inclined at an angle of 60 o above the horizontal, how much work does the father do on the wagon?

Kinetic Energy

Kinetic Energy due to motion ¢ K = ½ m v 2 ¢ K: Kinetic Energy l m: mass in kg l v: speed in m/s l ¢ Unit: Joules

Sample problem A 10. 0 g bullet has a speed of 1. 2 km/s. a) What is the kinetic energy of the bullet? b) What is the bullet’s kinetic energy if the speed is halved? c) What is the bullet’s kinetic energy if the speed is doubled?

The Work-Energy Theorem ¢ The net work due to all forces equals the change in the kinetic energy of a system. ¢ Wnet = K l Wnet: work due to all forces acting on an object l K: change in kinetic energy (Kf – Ki)

Sample problem An 8. 0 -g acorn falls from a tree and lands on the ground 10. 0 m below with a speed of 11. 0 m/s. a) What would the speed of the acorn have been if there had been no air resistance? b) Did air resistance do positive, negative or zero work on the acorn? Why?

Sample problem An 8. 0 -g acorn falls from a tree and lands on the ground 10. 0 m below with a speed of 11. 0 m/s. c) How much work was done by air resistance? d) What was the average force of air resistance?

Work done by variable forces

Constant force and work ¢ ¢ ¢ The force shown is a F(x) constant force. W = F r can be used to calculate the work done by this force when it moves an object from xa to xb. The area under the curve from xa to xb can also be used to calculate the work done by the force when it moves an object from xa to xb xa xb x

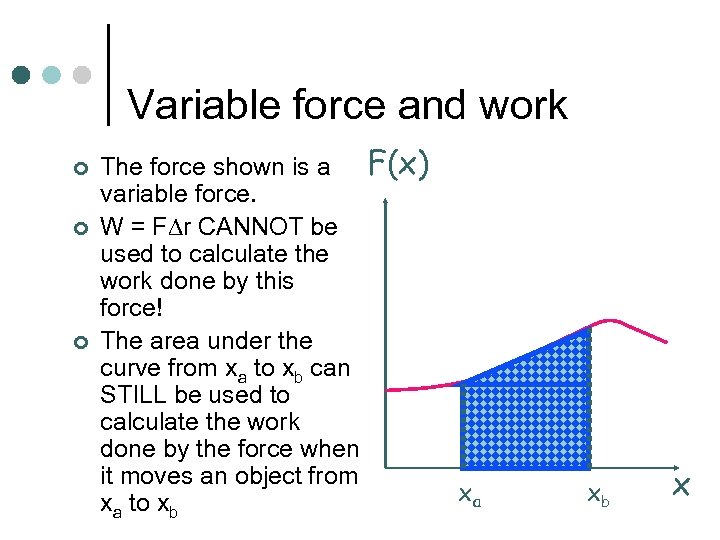Variable force and work ¢ ¢ ¢ The force shown is a F(x) variable force. W = F r CANNOT be used to calculate the work done by this force! The area under the curve from xa to xb can STILL be used to calculate the work done by the force when it moves an object from xa to xb xa xb x

Springs ¢ ¢ When a spring is stretched or compressed from its equilibrium position, it does negative work, since the spring pulls opposite the direction of motion. Ws = - ½ k x 2 l Ws: work done by spring (J) l k: force constant of spring (N/m) l x: displacement from equilibrium (m) The force doing the stretching does positive work equal to the magnitude of the work done by the spring. Wapp = - Ws = ½ k x 2

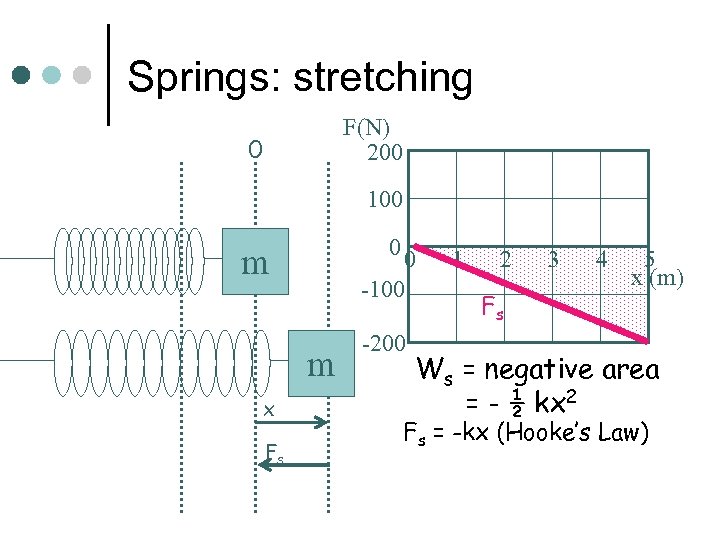Springs: stretching F(N) 200 0 100 0 m 0 -100 m x Fs -200 1 2 Fs 3 4 5 x (m) Ws = negative area = - ½ kx 2 Fs = -kx (Hooke’s Law)

Sample problem A spring with force constant 250 N/m is initially at its equilibrium length. a) How much work must you do to stretch the spring 0. 050 m? b) How much work must you do to compress it 0. 050 m?

Sample problem It takes 1000 J of work to compress a certain spring 0. 10 m. a) What is the force constant of the spring? b) To compress the spring an additional 0. 10 m, does it take 1000 J, more than 1000 J, or less than 1000 J? Verify your answer with a calculation.

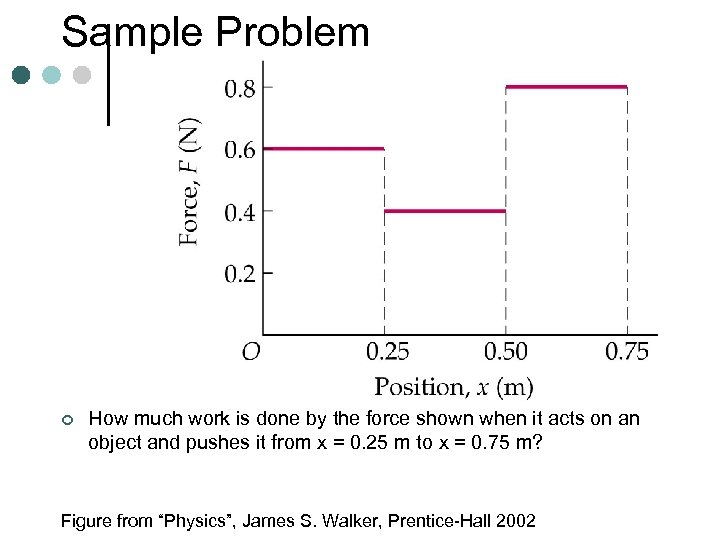Sample Problem ¢ How much work is done by the force shown when it acts on an object and pushes it from x = 0. 25 m to x = 0. 75 m? Figure from “Physics”, James S. Walker, Prentice-Hall 2002

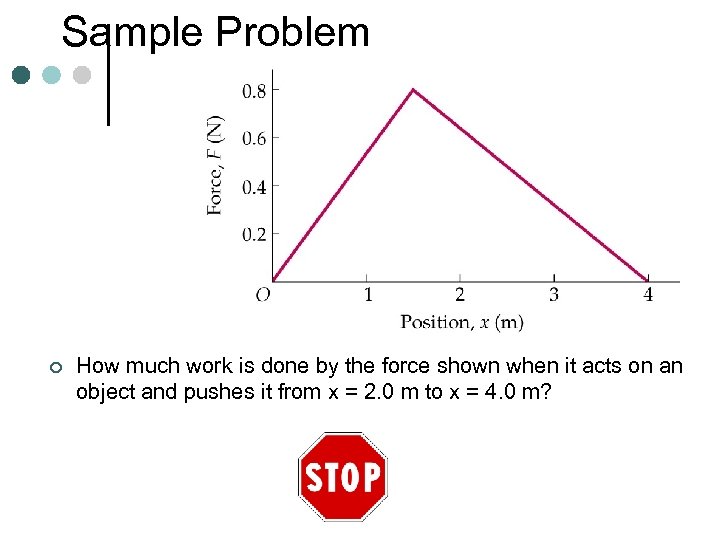Sample Problem ¢ How much work is done by the force shown when it acts on an object and pushes it from x = 2. 0 m to x = 4. 0 m?

Power

Power is the rate of which work is done. ¢ P = W/ t ¢ W: work in Joules l t: elapsed time in seconds l When we run upstairs, t is small so P is big. ¢ When we walk upstairs, t is large so P is small. ¢

Unit of Power ¢ SI unit for Power is the Watt. 1 Watt = 1 Joule/s l Named after the Scottish engineer James Watt (1776 -1819) who perfected the steam engine. l ¢ British system horsepower l 1 hp = 746 W l

How We Buy Energy… The kilowatt-hour is a commonly used unit by the electrical power company. ¢ Power companies charge you by the kilowatt-hour (k. Wh), but this not power, it is really energy consumed. ¢ 1 k. W = 1000 W ¢ 1 h = 3600 s ¢ 1 k. Wh = 1000 J/s • 3600 s = 3. 6 x 106 J ¢

Sample problem A man runs up the 1600 steps of the Empire State Building in 10 minutes and 59 seconds. If the height gain of each step was 0. 20 m, and the man’s mass was 70. 0 kg, what was his average power output during the climb? Give your answer in both watts and horsepower.

Sample problem Calculate the power output of a 1. 0 g fly as it walks straight up a window pane at 2. 0 cm/s.

Force types Forces acting on a system can be divided into two types according to how they affect potential energy. ¢ Conservative forces can be related to potential energy changes. ¢ Non-conservative forces cannot be related to potential energy changes. ¢ So, how exactly do we distinguish between these two types of forces? ¢

Conservative forces ¢ Work is path independent. l l ¢ Work along a closed path is zero. l ¢ ¢ If the starting and ending points are the same, no work is done by the force. Work changes potential energy. Examples: l l ¢ Work can be calculated from the starting and ending points only. The actual path is ignored in calculations. Gravity Spring force Conservation of mechanical energy holds!

Non-conservative forces ¢ Work is path dependent. l ¢ ¢ ¢ Work along a closed path is NOT zero. Work changes mechanical energy. Examples: l l ¢ Knowing the starting and ending points is not sufficient to calculate the work. Friction Drag (air resistance) Conservation of mechanical energy does not hold!

Potential energy Energy of position or configuration ¢ “Stored” energy ¢ For gravity: PE = mgh ¢ m: mass l g: acceleration due to gravity l h: height above the “zero” point l ¢ For springs: PEs = ½ k x 2 k: spring force constant l x: displacement from equilibrium position l

Conservative forces and Potential energy ¢ ¢ Wc = - U If a conservative force does positive work on a system, potential energy is lost. If a conservative force does negative work, potential energy is gained. For gravity l ¢ Wg = - Ug = -(mghf – mghi) For springs l Ws = - Us = -(½ k xf 2 – ½ k xi 2)

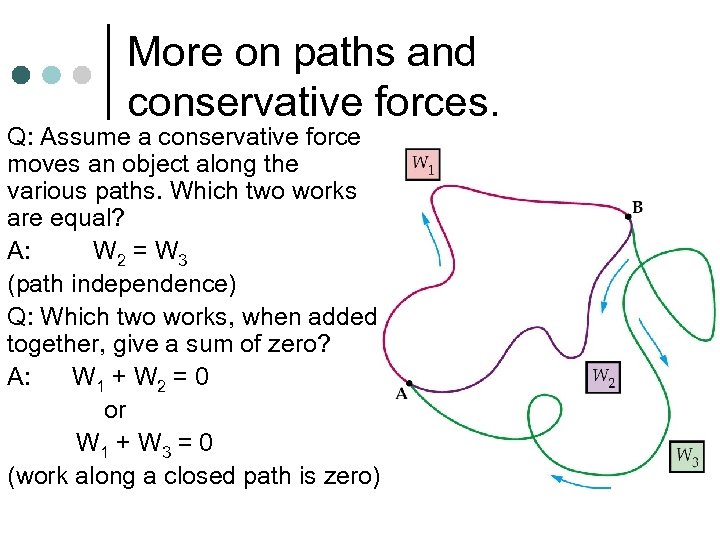More on paths and conservative forces. Q: Assume a conservative force moves an object along the various paths. Which two works are equal? A: W 2 = W 3 (path independence) Q: Which two works, when added together, give a sum of zero? A: W 1 + W 2 = 0 or W 1 + W 3 = 0 (work along a closed path is zero)

Conservative vs non -conservative forces

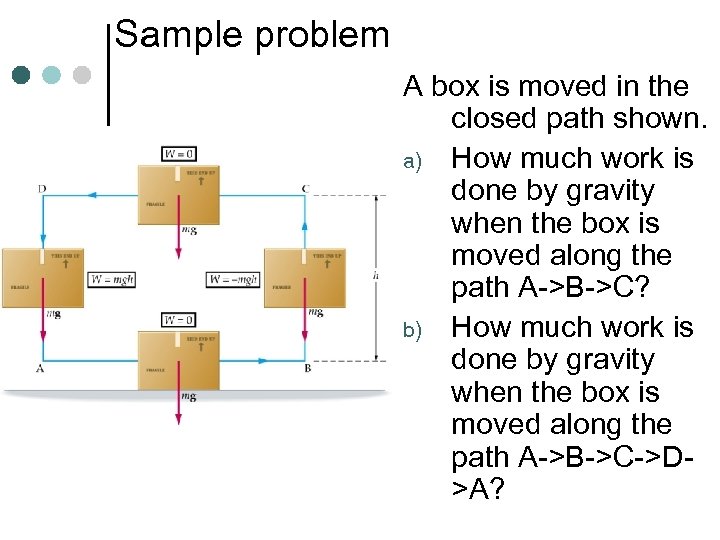Sample problem A box is moved in the closed path shown. a) How much work is done by gravity when the box is moved along the path A->B->C? b) How much work is done by gravity when the box is moved along the path A->B->C->D>A?

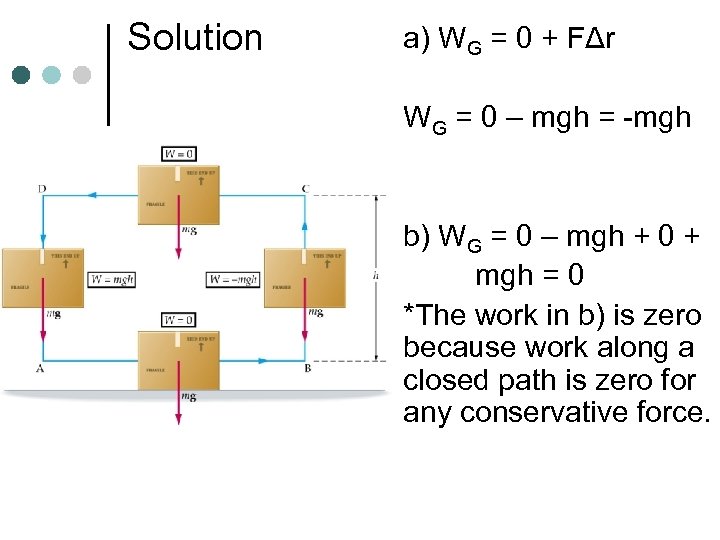Solution a) WG = 0 + FΔr WG = 0 – mgh = -mgh b) WG = 0 – mgh + 0 + mgh = 0 *The work in b) is zero because work along a closed path is zero for any conservative force.

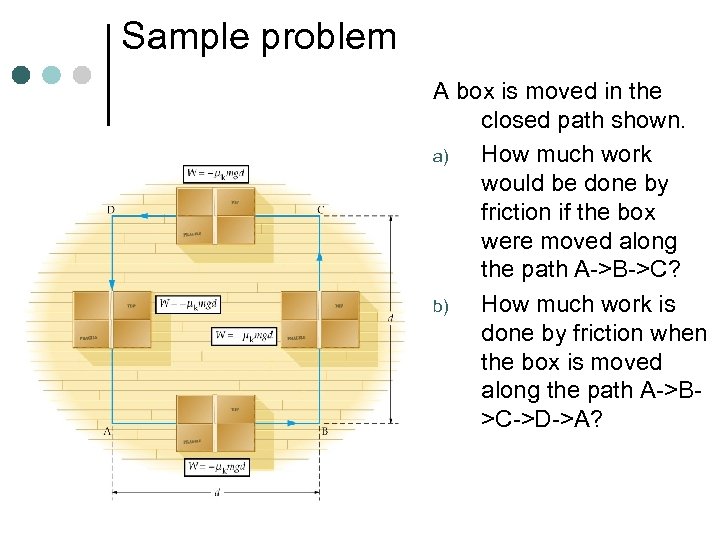Sample problem A box is moved in the closed path shown. a) How much work would be done by friction if the box were moved along the path A->B->C? b) How much work is done by friction when the box is moved along the path A->B>C->D->A?

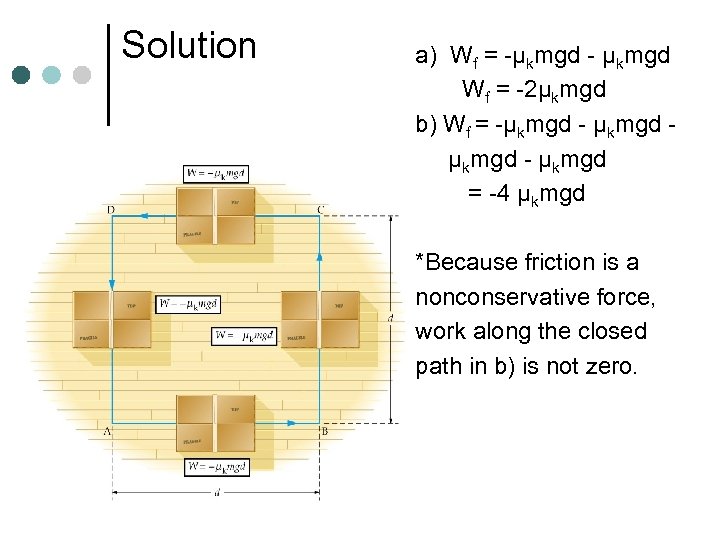Solution a) Wf = -µkmgd - µkmgd Wf = -2µkmgd b) Wf = -µkmgd - µkmgd = -4 µkmgd *Because friction is a nonconservative force, work along the closed path in b) is not zero.

Sample problem A diver drops to the water from a height of 20. 0 m, his gravitational potential energy decreases by 12, 500 J. How much does the diver weigh?

Sample problem If 30. 0 J of work are required to stretch a spring from a 2. 00 cm elongation to a 4. 00 cm elongation, how much work is needed to stretch it from a 4. 00 cm elongation to a 6. 00 cm elongation?

Conservation of Mechanical Energy

Law of Conservation of Energy In any isolated system, the total energy remains constant. ¢ Energy can neither be created nor destroyed, but can only be transformed from one type of energy to another. ¢

Law of Conservation of Mechanical Energy ¢ E = K + U = Constant K: Kinetic Energy (1/2 mv 2) l U: Potential Energy (gravity or spring) l ¢ E = U + K = 0 K: Change in kinetic energy l U: Change in gravitational or spring potential energy l

Roller Coaster Simulation Roller Coaster Physics Simulation (demonstrates gravitational potential energy and kinetic energy) Energy Skate Park

Pendulums and Energy Conservation Energy goes back and forth between K and U. ¢ At highest point, all energy is U. ¢ As it drops, U goes to K. ¢ At the bottom, energy is all K. ¢

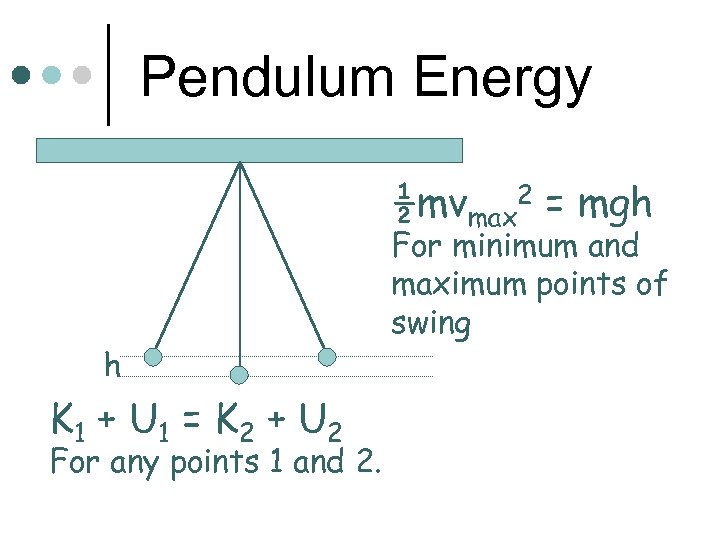Pendulum Energy ½mvmax 2 = mgh h K 1 + U 1 = K 2 + U 2 For any points 1 and 2. For minimum and maximum points of swing

Springs and Energy Conservation Transforms energy back and forth between K and U. ¢ When fully stretched or extended, all energy is U. ¢ When passing through equilibrium, all its energy is K. ¢ At other points in its cycle, the energy is a mixture of U and K. ¢

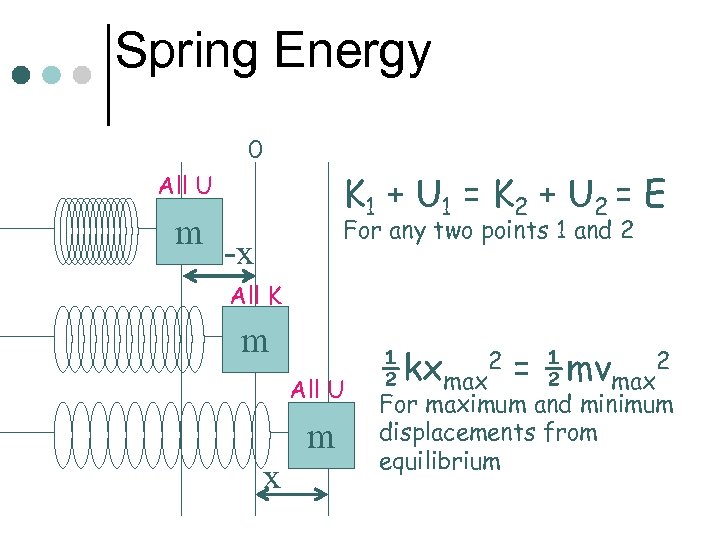Spring Energy 0 K 1 + U 1 = K 2 + U 2 = E All U m For any two points 1 and 2 -x All K m All U m x ½kxmax 2 = ½mvmax 2 For maximum and minimum displacements from equilibrium

Spring Simulation Spring Physics Simulation

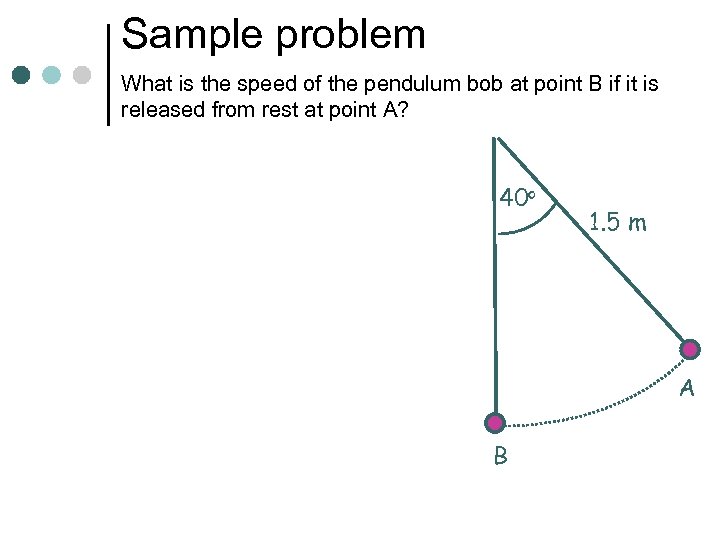Sample problem What is the speed of the pendulum bob at point B if it is released from rest at point A? 40 o 1. 5 m A B

Sample problem A 0. 21 kg apple falls from a tree to the ground, 4. 0 m below. Ignoring air resistance, determine the apple’s gravitational potential energy, U, kinetic energy, K, and total mechanical energy, E, when its height above the ground is each of the following: 4. 0 m, 2. 0 m, and 0. 0 m. Take ground level to be the point of zero potential energy.

Sample problem A 1. 60 kg block slides with a speed of 0. 950 m/s on a frictionless, horizontal surface until it encounters a spring with a force constant of 902 N/m. The block comes to rest after compressing the spring 4. 00 cm. Find the spring potential energy, U, the kinetic energy of the block, K, and the total mechanical energy of the system, E, for the following compressions: 0 cm, 2. 00 cm, 4. 00 cm.

Non-conservative forces and the Law of Conservation of Energy

Law of Conservation of Energy ¢ E = U + K + Eint= Constant l Eint is thermal energy. U + K + Eint = 0 ¢ Mechanical energy may be converted to and from heat. ¢

Work done by nonconservative forces ¢ Wnet = Wc + Wnc l Net work is done by conservative and non-conservative forces l Wc = - U • Potential energy is related to conservative forces only! l Wnet = K • Kinetic energy is related to net force (work-energy theorem) l K = - U + Wnc • From substitution ¢ Wnc = U + K = E l Nonconservative forces change mechanical energy. If nonconservative work is negative, as it often is, the mechanical energy of the system will drop.

Sample problem Catching a wave, a 72 -kg surfer starts with a speed of 1. 3 m/s, drops through a height of 1. 75 m, and ends with a speed of 8. 2 m/s. How much non-conservative work was done on the surfer?

Solution Wnc = ∆U + ∆K = Uf – Ui + K f – K i = mghf – mghi + ½ mvf 2 – ½ mvi 2 = m[g(hf – hi) + ½ (vf 2 – vi 2)] = 72[(9. 8)(0 - 1. 75) + ½ (8. 22 – 1. 32)] = 1125 J

Sample problem A 1. 75 -kg rock is released from rest at the surface of a pond 1. 00 m deep. As the rock falls, a constant upward force of 4. 10 N is exerted on it by water resistance. Calculate the nonconservative work, Wnc, done by the water resistance on the rock, the gravitational potential energy of the system, U, the kinetic energy of the rock, K, and the total mechanical energy of the system, E, for the following depths below the water’s surface: d = 0. 00 m, d = 0. 500 m, d = 1. 00 m. Let potential energy be zero at the bottom of the pond.

Solution for 0. 00 m Wnc = FΔr = 0 E=U+K = mgh + 0 = mgh = (1. 75 kg)(9. 8 m/s 2)(1. 00 m) = 17. 15 J Therefore Wnc = 0 (the rock hasn’t moved yet) E = 17. 15 J (will be reduced by the drag force of water) K = 0 (minimum value)

Solution for 0. 50 m Wnc = F∆r = (-4. 10 N)(0. 50 m) = -2. 05 J = ∆E E = 17. 15 J – ∆E = 17. 15 J - 2. 05 J = 15. 1 J E = U + K = mgh + K 15. 1 J = (1. 75 kg)(9. 8 m/s 2)(0. 50 m) + K 15. 1 J = 8. 6 J + K K = 15. 1 – 8. 6 J = 6. 5 J Therefore Wnc = -2. 05 J E = 15. 1 J (reduced by the drag force of water) U = 8. 6 J (determined by height) K = 6. 5 J (reduced by the drag force of water)

Solution for 1. 00 m Wnc = F∆r = (-4. 10 N)(1. 00 m) = -4. 10 J = ∆E E = 17. 15 J – ∆E = 17. 15 J - 4. 10 J = 13. 05 J E =U+K =0+K=K 13. 05 J = K Therefore Wnc = -4. 10 J E = 13. 05 J (reduced by the drag force of water) U = 0 (lowest point in problem) K = 13. 05 J (maximum value)

Conservation of Energy Laboratory

Pendulum lab ¢ ¢ Figure out how to demonstrate conservation of energy with a pendulum using the equipment provided. The photo-gates must be set up in “gate” mode this time. The width of the pendulum bob is an important number. To get it accurately, use the caliper. Turn in just your data, calculations, and result. Clearly show the speed you predict for the pendulum bob from conservation of energy, the speed you measure using the caliper and photo-gate data, and a % difference for the two.

Test