12a961c1459b03abc0ba4525527fa684.ppt
- Количество слайдов: 50
 Why ER Model? • ER modeling is relatively easy to learn and use • ERD shows a concise representation of the realworld in terms of entities and relationships • We know how to translate ERDs into relational schema • Most CASE tools support one or more variation of ERDs.
Why ER Model? • ER modeling is relatively easy to learn and use • ERD shows a concise representation of the realworld in terms of entities and relationships • We know how to translate ERDs into relational schema • Most CASE tools support one or more variation of ERDs.
 ER Model (Peter Chen 1976) • Representation • Constraints • Operations
ER Model (Peter Chen 1976) • Representation • Constraints • Operations
 Representation • Entity and Relationship. • The three main concepts of ER modeling at a lower level: Entity, Relationships, and Attributes. - Types of Entity: . . (Regular) entity: Has its own identifier . . Weak entity: Its identifier is the concatenation of the identifier of owner entity and its partial key. - Types of Relationships: . By degree: . . . Recursive relationship . . . Binary relationships . . . Ternary relationships
Representation • Entity and Relationship. • The three main concepts of ER modeling at a lower level: Entity, Relationships, and Attributes. - Types of Entity: . . (Regular) entity: Has its own identifier . . Weak entity: Its identifier is the concatenation of the identifier of owner entity and its partial key. - Types of Relationships: . By degree: . . . Recursive relationship . . . Binary relationships . . . Ternary relationships
 Constraints - Constraints of ER Models: (1) Cardinality constraints: 1: 1. 1: N, and M: N (2) Participation constraints: TOTAL (Mandatory) and PARTIAL (Optional) - Entity constraints -- The identifier of an entity cannot be null -- Weak entity constraints -- The concatenated identifier of the weak entity -- Existence dependency
Constraints - Constraints of ER Models: (1) Cardinality constraints: 1: 1. 1: N, and M: N (2) Participation constraints: TOTAL (Mandatory) and PARTIAL (Optional) - Entity constraints -- The identifier of an entity cannot be null -- Weak entity constraints -- The concatenated identifier of the weak entity -- Existence dependency
 Operations - What kinds of operations does the ER model inherently support? - There have been many research proposals that automatically navigate the ERD to process queries. - However, since we use the ERD as a high level design tool and translate the ERD into RDB, they are not important to our discussion.
Operations - What kinds of operations does the ER model inherently support? - There have been many research proposals that automatically navigate the ERD to process queries. - However, since we use the ERD as a high level design tool and translate the ERD into RDB, they are not important to our discussion.
 Characteristics of Next Generation Databases In this part, we will briefly look at recent trends in database technology. Database systems which will come in next decade is referred to as Next Generation database systems.
Characteristics of Next Generation Databases In this part, we will briefly look at recent trends in database technology. Database systems which will come in next decade is referred to as Next Generation database systems.
 Characteristics of Next Generation Databases • Rich data model-- which means the new data models will have more data modeling components than ER or relational data model - Object-oriented - Multimedia data - Choices for structures, unstructures • Highly distributed - Heterogeneous environment, WWW - Self-installing, self-managed, highly robust and automatic coordination
Characteristics of Next Generation Databases • Rich data model-- which means the new data models will have more data modeling components than ER or relational data model - Object-oriented - Multimedia data - Choices for structures, unstructures • Highly distributed - Heterogeneous environment, WWW - Self-installing, self-managed, highly robust and automatic coordination
 Cont. • Large storage and memory - Will have more RAM - Many commercial DB systems will have tera/peta/exa/ zetta/yotta bytes or more • Component DBMS, DB applications may be built by buying components as we buy HW components - Supportable DBMSs - Need to have public interfaces • High-level environment - High level query languages and supporting tools • Intelligent processing
Cont. • Large storage and memory - Will have more RAM - Many commercial DB systems will have tera/peta/exa/ zetta/yotta bytes or more • Component DBMS, DB applications may be built by buying components as we buy HW components - Supportable DBMSs - Need to have public interfaces • High-level environment - High level query languages and supporting tools • Intelligent processing
 Technologies for Next Generation Databases • Traditional Database Technology: Extended RDBMS (Relational Technology, Semantic Data models, 4 GL, CASE) • Object-oriented Technology: OODBMS, ORDBMS, OOA&D, OOP (Rich data model, Natural representation, SW development, Integration, Productivity, Reusability, Component-based) • Knowledge Based Techniques: Expert DBMS (Inference, AI Technology, Tools for User Interface, Data Mining, and Knowledge Acquisition, etc. ) • Hypermedia: Multimedia DBMS (User Interface, Multimedia data, GIS, Imaging DB, VOD (Video on demand)) • Online Information Retrieval: (Text database, Information Retrieval, Intelligent Retrieval)
Technologies for Next Generation Databases • Traditional Database Technology: Extended RDBMS (Relational Technology, Semantic Data models, 4 GL, CASE) • Object-oriented Technology: OODBMS, ORDBMS, OOA&D, OOP (Rich data model, Natural representation, SW development, Integration, Productivity, Reusability, Component-based) • Knowledge Based Techniques: Expert DBMS (Inference, AI Technology, Tools for User Interface, Data Mining, and Knowledge Acquisition, etc. ) • Hypermedia: Multimedia DBMS (User Interface, Multimedia data, GIS, Imaging DB, VOD (Video on demand)) • Online Information Retrieval: (Text database, Information Retrieval, Intelligent Retrieval)
 Cont’ • Internet, Networking & Distributed systems (WWW interface, internet/intranet, Heterogeneous, Resourcesharing, Robust and automatic coordination, Legacy systems, Client/Server) • Mass Storage (Optical disks, Scanning, Electronic publishing, Digital library, DIS) • Other trends - Standards (SQL 3, OMG, ODMG, CORBA, DCOM. . . ) - High-level environment (HLQL, supporting tools) - Component databases (public interface, interoperable, portable) - Larger memory - Parallelism - New applications (Data Warehousing, Electronic Commerce, Health-care systems, EOSDIS, . . . )
Cont’ • Internet, Networking & Distributed systems (WWW interface, internet/intranet, Heterogeneous, Resourcesharing, Robust and automatic coordination, Legacy systems, Client/Server) • Mass Storage (Optical disks, Scanning, Electronic publishing, Digital library, DIS) • Other trends - Standards (SQL 3, OMG, ODMG, CORBA, DCOM. . . ) - High-level environment (HLQL, supporting tools) - Component databases (public interface, interoperable, portable) - Larger memory - Parallelism - New applications (Data Warehousing, Electronic Commerce, Health-care systems, EOSDIS, . . . )
 Normalization - Basic concepts of normalization - Functional Dependency (FD) -- Definitions and Semantics -- FD as integrity constraints -- Armstrong's axioms -- Minimal cover - Lossless join and spurious tuples - Normal forms (1, 2, 3, 4, 5) -- Multi-valued dependencies & 4 NF -- Join dependencies & 5 NF - Practical ways to use normalization - Denormaliztion techniques
Normalization - Basic concepts of normalization - Functional Dependency (FD) -- Definitions and Semantics -- FD as integrity constraints -- Armstrong's axioms -- Minimal cover - Lossless join and spurious tuples - Normal forms (1, 2, 3, 4, 5) -- Multi-valued dependencies & 4 NF -- Join dependencies & 5 NF - Practical ways to use normalization - Denormaliztion techniques
 What is the normalization? A process to design a highly desirable relational schemas using relational theory
What is the normalization? A process to design a highly desirable relational schemas using relational theory
 Why Normalization? - Normal forms are guidelines for relational database design -- Minimize redundancy -- Avoid potential inconsistency - Can predict the behavior (problems) of database systems - Avoid update anomalies discussed below
Why Normalization? - Normal forms are guidelines for relational database design -- Minimize redundancy -- Avoid potential inconsistency - Can predict the behavior (problems) of database systems - Avoid update anomalies discussed below
 What if we don't normalize our DB schema? • Your DB will have the following update anomalies. • Insertion problem • Deletion problem • Update problem
What if we don't normalize our DB schema? • Your DB will have the following update anomalies. • Insertion problem • Deletion problem • Update problem
 Hierarchy of normal forms • The normal forms from less strict to more strict: 1 NF, 2 NF, 3 NF, BCNF, 4 NF, 5 NF • We can directly decompose into BCNF or 3 NF without going through 2 NF. • Note that BCNF (Boyce-Codd normal form) is a variation of 3 NF. In most cases, 3 NF and BCNF are the same and we will not discuss it in this course.
Hierarchy of normal forms • The normal forms from less strict to more strict: 1 NF, 2 NF, 3 NF, BCNF, 4 NF, 5 NF • We can directly decompose into BCNF or 3 NF without going through 2 NF. • Note that BCNF (Boyce-Codd normal form) is a variation of 3 NF. In most cases, 3 NF and BCNF are the same and we will not discuss it in this course.
 FD (Functional Dependency) • FD is a way of representing relationships among attributes in a relation. • Notation: X --> Y, where both X and Y can be a group of attributes, X: LHS, Y: RHS We say that 1. X uniquely determines Y, 2. For a given value of X, there is at most one value of Y associated with X at a time.
FD (Functional Dependency) • FD is a way of representing relationships among attributes in a relation. • Notation: X --> Y, where both X and Y can be a group of attributes, X: LHS, Y: RHS We say that 1. X uniquely determines Y, 2. For a given value of X, there is at most one value of Y associated with X at a time.
 Example Suppose we have R(A, B, C, D, E, F) and data instances as follows: A B C D E F a 1 b 1 c 1 d 1 e 1 f 1 a 1 b 2 c 1 d 1 e 2 f 2 a 2 b 2 c 2 d 1 e 2 f 2 a 3 b 3 c 1 d 2 e 3 f 1
Example Suppose we have R(A, B, C, D, E, F) and data instances as follows: A B C D E F a 1 b 1 c 1 d 1 e 1 f 1 a 1 b 2 c 1 d 1 e 2 f 2 a 2 b 2 c 2 d 1 e 2 f 2 a 3 b 3 c 1 d 2 e 3 f 1
 Which one is valid? Based on relation above, which of the following FDs are valid? (a) A -> C (b) C -> A (c) B -> E (d) C -> D (e) B -> F (f) BD -> E (g) CD -> E (h) F -> B
Which one is valid? Based on relation above, which of the following FDs are valid? (a) A -> C (b) C -> A (c) B -> E (d) C -> D (e) B -> F (f) BD -> E (g) CD -> E (h) F -> B
 SELECTIVE ANSWERS: (a) A --> C: This is True since for each a 1 value, we have the same c 1. Note that it doesn't matter that both a 1 and a 3 ends up with the same c 1. This is similar to the fact that two different employees may have the same age. (b) C --> A: This is false since c 1 maps to both a 1 and a 3. The examples of (a) and (b) show that FDs are not symmetric. That is, the fact that A-->C is true doesn't mean C--> A is true. (c) B --> E is True (d) C --> D is False. (f) BD--> E is True. Since we have two attributes in LHS, we have to consider the pair of value together as a single of the LHS. (g) CD -> E is False.
SELECTIVE ANSWERS: (a) A --> C: This is True since for each a 1 value, we have the same c 1. Note that it doesn't matter that both a 1 and a 3 ends up with the same c 1. This is similar to the fact that two different employees may have the same age. (b) C --> A: This is false since c 1 maps to both a 1 and a 3. The examples of (a) and (b) show that FDs are not symmetric. That is, the fact that A-->C is true doesn't mean C--> A is true. (c) B --> E is True (d) C --> D is False. (f) BD--> E is True. Since we have two attributes in LHS, we have to consider the pair of value together as a single of the LHS. (g) CD -> E is False.
 FD The FDs in a given relation are determined by semantics of the relation, not by data instances.
FD The FDs in a given relation are determined by semantics of the relation, not by data instances.
 Example TEACH (Teacher, Course, Text) Teacher Course Text Smith DS Bartram Smith DBMS Al-nour Hall Compilers Hoffman Brown DS Augen
Example TEACH (Teacher, Course, Text) Teacher Course Text Smith DS Bartram Smith DBMS Al-nour Hall Compilers Hoffman Brown DS Augen
 Example - TEACH looks to satisfy TEXT --> COURSE since each text ends up with different course. - However, it doesn't semantically make sense to determine the course by the text book since two different courses could use the same book. SO, TEXT --> COURSE is False. - However, instances can be used to disprove a FD TEACHER --> COURSE since two teacher (Smith) teaches two different courses. - The correct FD of this relation is TEACHER+COURSE --> TEXT. - What else can be disproved from the above data instances?
Example - TEACH looks to satisfy TEXT --> COURSE since each text ends up with different course. - However, it doesn't semantically make sense to determine the course by the text book since two different courses could use the same book. SO, TEXT --> COURSE is False. - However, instances can be used to disprove a FD TEACHER --> COURSE since two teacher (Smith) teaches two different courses. - The correct FD of this relation is TEACHER+COURSE --> TEXT. - What else can be disproved from the above data instances?
 FD FD as an integrity constraint Example WORK (EMP#, DEPT, LOC) FDs of WORK are: EMP# --> DEPT --> LOC
FD FD as an integrity constraint Example WORK (EMP#, DEPT, LOC) FDs of WORK are: EMP# --> DEPT --> LOC
 Example Suppose WORK table has the following three instances: EMP# E 1 E 2 E 3 DEPT D 1 D 2 D 1 LOC Market Walnut Market
Example Suppose WORK table has the following three instances: EMP# E 1 E 2 E 3 DEPT D 1 D 2 D 1 LOC Market Walnut Market
 Example Which of the following are valid or invalid? and why? (Hints: check whether or not your insertion or update would violate any existing FD!) INSERT UPDATE (1) E 1 D 1 Walnut (2) E 1 D 2 Walnut (3) E 5 D 3 Market
Example Which of the following are valid or invalid? and why? (Hints: check whether or not your insertion or update would violate any existing FD!) INSERT UPDATE (1) E 1 D 1 Walnut (2) E 1 D 2 Walnut (3) E 5 D 3 Market
 SOLUTION for INSERTION (1) The first insertion is invalid since doing so would violate the FD DEPT--> LOC. (2) The second insertion is also invalid since doing so would violate the FD EMP#--> DEPT (3) The third insertion is allowed since doing so does not violate any FD.
SOLUTION for INSERTION (1) The first insertion is invalid since doing so would violate the FD DEPT--> LOC. (2) The second insertion is also invalid since doing so would violate the FD EMP#--> DEPT (3) The third insertion is allowed since doing so does not violate any FD.
 SOLUTION FOR UPDATE (1) This means changing Market to Walnut. This update would violate FD DEPT --> LOC. (2) This means changing E 2 of the 2 nd tuple to E 1. This update would violate FD EMP# --> DEPT (3) The third update is INSERTION and valid
SOLUTION FOR UPDATE (1) This means changing Market to Walnut. This update would violate FD DEPT --> LOC. (2) This means changing E 2 of the 2 nd tuple to E 1. This update would violate FD EMP# --> DEPT (3) The third update is INSERTION and valid
 Example BORROW (Loan#, Bname, Cname, Amount) and FDs: Loan# --> Amount Loan# --> Bname What is the semantic difference between the following two FDs? (1) Loan# --> Cname (2) Loan# --> Cname
Example BORROW (Loan#, Bname, Cname, Amount) and FDs: Loan# --> Amount Loan# --> Bname What is the semantic difference between the following two FDs? (1) Loan# --> Cname (2) Loan# --> Cname
 Example (1) means there is only one customer for each loan, which means a loan cannot be checked out by the husband wife together, for example. (2) means for each loan, they may be more than customers
Example (1) means there is only one customer for each loan, which means a loan cannot be checked out by the husband wife together, for example. (2) means for each loan, they may be more than customers
 How to find FDs? - List only most direct FDs, not indirect FDs (e. g. , SSN --> DLOC is an indirect FD) - List only non-trivial FDs (e. g. , SSN --> SSN is a trivial FD) - Do not include redundant attributes in an FD in either LHS or RHS (e. g. , SSN, ENAME --> ENAME, BDATE, ADDRESS has a redundant attribute in LHS (ENAME))
How to find FDs? - List only most direct FDs, not indirect FDs (e. g. , SSN --> DLOC is an indirect FD) - List only non-trivial FDs (e. g. , SSN --> SSN is a trivial FD) - Do not include redundant attributes in an FD in either LHS or RHS (e. g. , SSN, ENAME --> ENAME, BDATE, ADDRESS has a redundant attribute in LHS (ENAME))
 Example from Book: EMP_DEPT (ENAME, SSN, BDATE, ADDRESS, DNUMBER, DNAME, DMGRSSN, DLOC) The valid FDs in this relation are: (1) SSN --> ENAME, BDATE, ADDRESS, DNUMBER (2) DNUMBER --> DNAME, DMGRSSN, DLOC
Example from Book: EMP_DEPT (ENAME, SSN, BDATE, ADDRESS, DNUMBER, DNAME, DMGRSSN, DLOC) The valid FDs in this relation are: (1) SSN --> ENAME, BDATE, ADDRESS, DNUMBER (2) DNUMBER --> DNAME, DMGRSSN, DLOC
 Transitive dependency (TD) If A --> B and B --> C, then A --> C is called a TD.
Transitive dependency (TD) If A --> B and B --> C, then A --> C is called a TD.
 Find a TD in the above EMP_DEPT One TD is: SSN --> DNAME since SSN --> DNUMBER and DNUMBER --> DNAME. Two other TDs are SSN --> DMGRSSN and SSN --> DLOC
Find a TD in the above EMP_DEPT One TD is: SSN --> DNAME since SSN --> DNUMBER and DNUMBER --> DNAME. Two other TDs are SSN --> DMGRSSN and SSN --> DLOC
 Candidate key (CK) and FDs The CK can determine all other attributes of the R(A, B, C, D, E, F). Suppose we have two CKs, CK = {A, BD} Then, A --> B, C, D, E. F BD --> A, C, E, F
Candidate key (CK) and FDs The CK can determine all other attributes of the R(A, B, C, D, E, F). Suppose we have two CKs, CK = {A, BD} Then, A --> B, C, D, E. F BD --> A, C, E, F
 Algorithm for Finding a Key Once we find a minimal cover, we can find a key using the following algorithm. • (1) Find attributes not appearing in the RHS of any FDs. Then, these are part of any candidate keys. • (2) Check whether they can determine all other attributes by using FDs. • (3) If not, what other attributes do I need to add to determine all other attributes?
Algorithm for Finding a Key Once we find a minimal cover, we can find a key using the following algorithm. • (1) Find attributes not appearing in the RHS of any FDs. Then, these are part of any candidate keys. • (2) Check whether they can determine all other attributes by using FDs. • (3) If not, what other attributes do I need to add to determine all other attributes?
 Examples STORE (SNAME, ADDR, ZIP, ITEM, PRICE) FDs: SNAME --> ADDR --> ZIP SNAME, ITEM --> PRICE
Examples STORE (SNAME, ADDR, ZIP, ITEM, PRICE) FDs: SNAME --> ADDR --> ZIP SNAME, ITEM --> PRICE
 Finding a key: (1) SNAME does not appear in RHS, so SNAME must be a part of the key. (2) since SNAME --> ADDR --> ZIP, we know SNAME --> ADDR, ZIP (3) But SNAME alone cannot determine any more. How can we determine ITEM and PRICE ? If we have ITEM, then we can determine PRICE So, SNAME, ITEM --> SNAME, ADDR, ZIP, ITEM, PRICE so it satisfies the definition of the key.
Finding a key: (1) SNAME does not appear in RHS, so SNAME must be a part of the key. (2) since SNAME --> ADDR --> ZIP, we know SNAME --> ADDR, ZIP (3) But SNAME alone cannot determine any more. How can we determine ITEM and PRICE ? If we have ITEM, then we can determine PRICE So, SNAME, ITEM --> SNAME, ADDR, ZIP, ITEM, PRICE so it satisfies the definition of the key.
 Examples of Finding a Key for relation R (A, B, C, D) FDs A--> C B --> D C --> D (a) (b) A -->B B --> C A --> D D --> A (c) A --> D D --> A C --> B Key
Examples of Finding a Key for relation R (A, B, C, D) FDs A--> C B --> D C --> D (a) (b) A -->B B --> C A --> D D --> A (c) A --> D D --> A C --> B Key
 ANSWER • (a) {AB} • (b) {A, D} Note that A and D are in 1: 1 relationship since A --> D and D --> A. • (c) {CA, CD} Note that A-->D and D --> A.
ANSWER • (a) {AB} • (b) {A, D} Note that A and D are in 1: 1 relationship since A --> D and D --> A. • (c) {CA, CD} Note that A-->D and D --> A.
 Lossless-Decomposition and Spurious Tuples - Decomposition means dividing a table into multiple tables. - Decomposition is lossless if it is possible to reconstruct R from decomposed relations using JOINs. • Condition for Lossless Join when R was decomposed into R 1, R 2, . . , Rn • R = R 1¥ R 2 ¥ R 3 ¥. . ¥ Rn, where ¥ means JOIN operation. •
Lossless-Decomposition and Spurious Tuples - Decomposition means dividing a table into multiple tables. - Decomposition is lossless if it is possible to reconstruct R from decomposed relations using JOINs. • Condition for Lossless Join when R was decomposed into R 1, R 2, . . , Rn • R = R 1¥ R 2 ¥ R 3 ¥. . ¥ Rn, where ¥ means JOIN operation. •
 Cont. • Why need it ? To maintain the accurate database • What if not ? Cause wrong answers for queries • How to check ? It is sufficient if any Ri contains a candidate key of R • when we used the normalization algorithms for 3 NF/BCNF
Cont. • Why need it ? To maintain the accurate database • What if not ? Cause wrong answers for queries • How to check ? It is sufficient if any Ri contains a candidate key of R • when we used the normalization algorithms for 3 NF/BCNF
 Cont. This means that if any of the decomposed relation contains a CK (or PK) of the original relation, then the decomposition is called lossless. This means by joining all the decomposed relations, we can reconstruct the original relation
Cont. This means that if any of the decomposed relation contains a CK (or PK) of the original relation, then the decomposition is called lossless. This means by joining all the decomposed relations, we can reconstruct the original relation
 Example LOAN_ACC (L#, AMT, ACC#, BAL) L# --> AMT ACC# --> BAL Key ? L# + ACC# Possible decomposition: R 1(L#, AMT) R 2 (ACC#, BAL) The decomposition is not loss-less, since R 1 or R 2 does not have a candidate key. (Note that we cannot correlate L# and ACC#)
Example LOAN_ACC (L#, AMT, ACC#, BAL) L# --> AMT ACC# --> BAL Key ? L# + ACC# Possible decomposition: R 1(L#, AMT) R 2 (ACC#, BAL) The decomposition is not loss-less, since R 1 or R 2 does not have a candidate key. (Note that we cannot correlate L# and ACC#)
 Example) WORK (EMP#, DEPT, LOC) EMP# --> DEPT --> LOC Key ? EMP#, since EMP# --> DEPT, LOC Decomposition R 1 (EMP#, DEPT) R 2(DEPT, LOC) The decomposition is lossless, since R 1 contains a candidate key.
Example) WORK (EMP#, DEPT, LOC) EMP# --> DEPT --> LOC Key ? EMP#, since EMP# --> DEPT, LOC Decomposition R 1 (EMP#, DEPT) R 2(DEPT, LOC) The decomposition is lossless, since R 1 contains a candidate key.
 Spurious Tuples • Spurious Tuples are those that appear in the result of lossy decomposition, but that do not exist in the original relation R. •
Spurious Tuples • Spurious Tuples are those that appear in the result of lossy decomposition, but that do not exist in the original relation R. •
 Example) A a 1 a 2 a 3 B b 1 b 2 C c 1 c 2
Example) A a 1 a 2 a 3 B b 1 b 2 C c 1 c 2
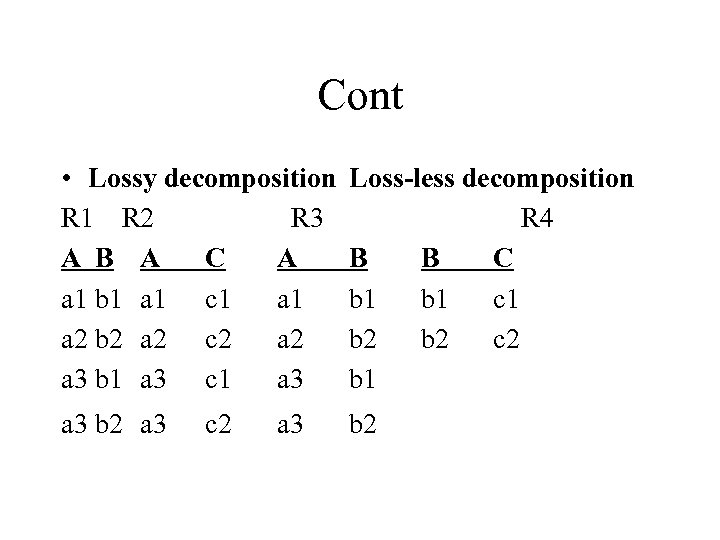 Cont • Lossy decomposition R 1 R 2 R 3 A B A C A a 1 b 1 a 1 c 1 a 2 b 2 a 2 c 2 a 3 b 1 a 3 c 1 a 3 Loss-less decomposition R 4 B B C b 1 c 1 b 2 c 2 b 1 a 3 b 2 c 2 a 3
Cont • Lossy decomposition R 1 R 2 R 3 A B A C A a 1 b 1 a 1 c 1 a 2 b 2 a 2 c 2 a 3 b 1 a 3 c 1 a 3 Loss-less decomposition R 4 B B C b 1 c 1 b 2 c 2 b 1 a 3 b 2 c 2 a 3
 Perform the join between R 1(A, B) ¥ R 2(A, C): A a 1 a 2 a 3 a 3 B b 1 b 2 C c 1 c 2* c 1* c 2
Perform the join between R 1(A, B) ¥ R 2(A, C): A a 1 a 2 a 3 a 3 B b 1 b 2 C c 1 c 2* c 1* c 2
 Cont The two tuples with * are spurious tuples that do not exist in the original relation R. - Perform the join between R 3(A, B)¥ R 4(B, C): The result should be the same as the original R.
Cont The two tuples with * are spurious tuples that do not exist in the original relation R. - Perform the join between R 3(A, B)¥ R 4(B, C): The result should be the same as the original R.
 Questions: Why does R 1 JOIN R 2 cause lossy decomposition and result in spurious tuples? • Because the decomposition of R into R 1 and R 2 didn't follow the FDs. • The FDs in R are: A --> B B --> C • The decomposition that follows the FDs are lossless as shown in R 3(A, B) and R 4(B, C). • This means: - When we normalize we decompose based on FDs, not randomly. - After decomposition, one of decomposed relation Ri must contain a CK to be lossless.
Questions: Why does R 1 JOIN R 2 cause lossy decomposition and result in spurious tuples? • Because the decomposition of R into R 1 and R 2 didn't follow the FDs. • The FDs in R are: A --> B B --> C • The decomposition that follows the FDs are lossless as shown in R 3(A, B) and R 4(B, C). • This means: - When we normalize we decompose based on FDs, not randomly. - After decomposition, one of decomposed relation Ri must contain a CK to be lossless.


