Why Canadian fur trappers should stay in bed

Why Canadian fur trappers should stay in bed when they have the flu: modeling the geographic spread of infectious diseases Lisa Sattenspiel Department of Anthropology University of Missouri-Columbia

Major approaches to modeling the transmission of infectious diseases • Deterministic compartmental models (systems of differential equations) • Statistical approaches (e. g. , regression analysis, time series analysis, generalized linear models, spatial statistics) • Stochastic compartmental models (e. g. chain binomial model) • Individual-based mathematical models • Computer-based models – Microsimulations – Agent-based models

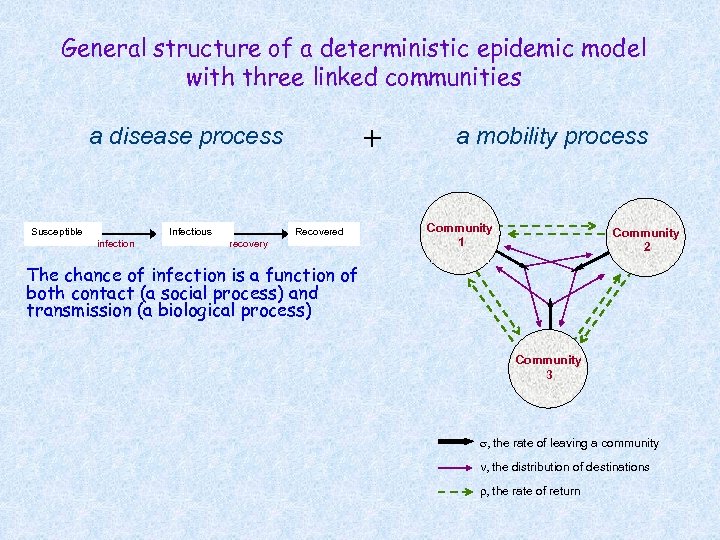
General structure of a deterministic epidemic model with three linked communities + a disease process Susceptible Infectious infection Recovered recovery a mobility process Community 1 Community 2 The chance of infection is a function of both contact (a social process) and transmission (a biological process) Community 3 , the rate of leaving a community , the distribution of destinations , the rate of return

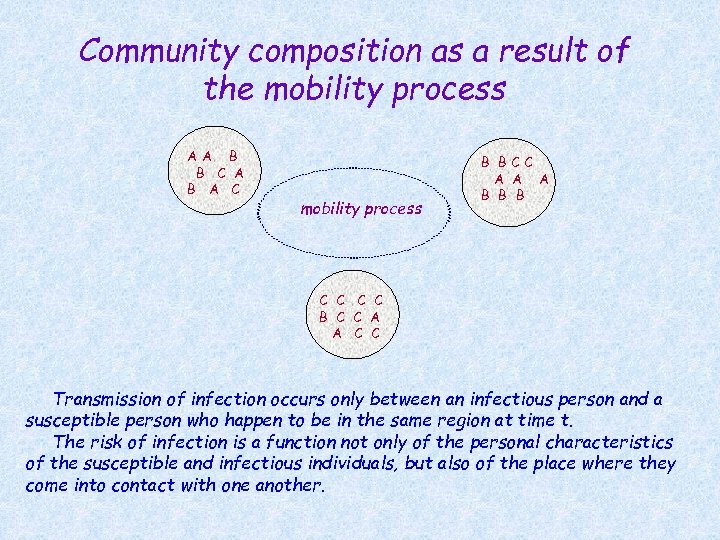
Community composition as a result of the mobility process AA B B C A B A C mobility process B BCC A A A B B B C C A A C C Transmission of infection occurs only between an infectious person and a susceptible person who happen to be in the same region at time t. The risk of infection is a function not only of the personal characteristics of the susceptible and infectious individuals, but also of the place where they come into contact with one another.

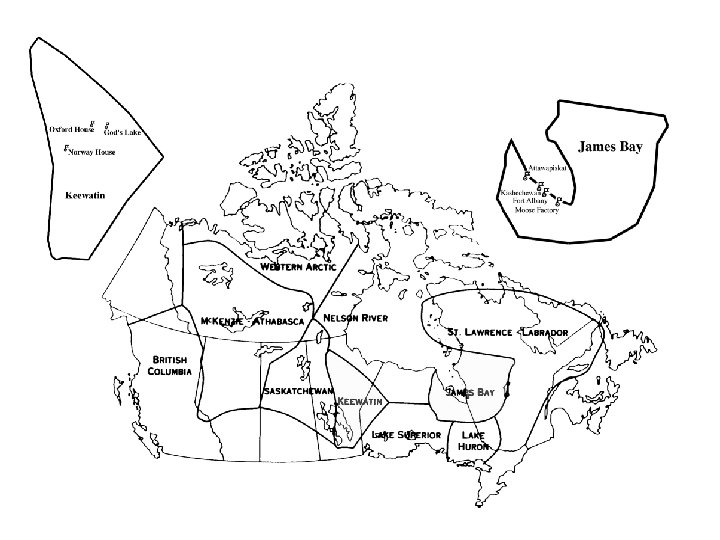
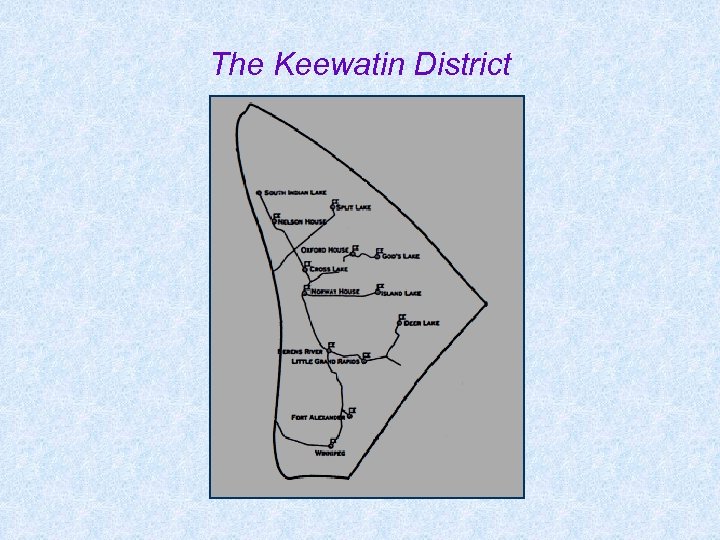
The Keewatin District

The environment at and near Norway House

Mortality before, during, and after the flu epidemic

Mortality among communities within Manitoba

Distribution of deaths by family Norway House 1919 237 families significantly fewer observed G-value = 17. 33, p < 0. 05, df = 2

Families with three to five deaths Norway House 1919

Initial questions a) b) How do changes in the rates and patterns of mobility affect epidemic spread? How do changes in rates of contact within communities affect epidemic spread?

Changing social organization by varying the contact rate within communities DOES lead to significant changes in the size and timing of epidemic peaks

Some of the questions addressed in the project 1) 2) 3) 4) 5) How do changes in frequency and direction of travel among socially linked communities influence patterns of disease spread within and among those communities? How do differences in rates of contact and other aspects of social structure within communities affect epidemic transmission within and among communities? What is the effect of different types of settlement structures and economic relationships among communities on patterns of epidemic spread? What was the impact of quarantine policies on the spread of the flu through the study communities? Do we see the same kinds of results with other diseases and in other locations and time periods?

BUT the real study populations are so small that the deterministic models presented so far are not really the best ones to use. Solution: Develop an individual-based epidemic model that can deal with the variability of individual behaviors and the stochasticity that results when populations are small

Seasonal differences in social organization in the northern fur trade • • Social group size and composition Dispersal on the land Resource availability Modes of travel Travel routes Numbers traveling Time to complete a journey

Stage 1 Develop a single-post agentbased model that captures significant aspects of the community structure at the main post, Norway House

Summer Epidemics: short duration, high peak, peak quickly Winter Epidemics: long duration, low peak, peak slowly

Stage 2 Extend the Stage 1 model to three posts so that results can be compared directly to those from the deterministic model

NHOHGL Model NHODE Model Predicted Number Infected at NH 717 190 Predicted Number Infected at OH 7 7 Predicted Number Infected at GL 0 7 Predicted Extent of Epidemic Spread Rarely reaches OH, never reaches GL Epidemic routinely reaches both OH and GL Shape of the Epidemic Curve an initial case building up to a rather short and defined epidemic peak. Timing of the epidemic peaks First at NH Predicted Impact of Seasonality Summer epidemic has earlier and more severe peak Result of the Introduction of the flu at OH or GL instead of NH Epidemic fails to spread; nearly all epidemic totals are impacted Epidemic spreads more readily; timing of the epidemic is affected but not the severity Parameters that influence the timing of the epidemic mobility, travel patterns, contact rates, and population parameters Mobility, travel patterns, and contact rates Parameters that Influence the spread of the epidemic mobility, travel patterns, contact rates, and population parameters Mobility and travel patterns Parameters that Influence Epidemic severity mobility, travel patterns, contact rates, and population parameters Contact rates

Major potential contributions of mathematical models to human disease research • Focus research efforts on factors most likely to have a significant impact on patterns of epidemic spread. – Simulation results illuminated relative roles of population mobility and social contact within communities on infectious disease spread and shifted focus to factors influencing social contact. • Identify critical areas with insufficient data. – Results stimulated new archival searches to find data on settlement structure and seasonal activities. • Help to understand conditions under which infectious diseases emerge and spread across a landscape. – Simulations showed, for example, that patterns of mobility influence the timing of epidemic peaks and the patterns of an epidemic’s spread across space.

Major potential contributions of mathematical models to human disease research (cont. ) • • • May help to identify potential hot spots for the evolution of new diseases. – Simulations indicated the importance of communities taking a central role in a region, suggesting that these communities are potential hot spots in their regions. Allow for “experimentation” on human populations that would be impossible or unethical in the real world. – Infectious disease simulations follow the progress of potential epidemics within communities. Well-structured models that are grounded in high quality data provide valuable inferences with which to predict the impact of future epidemics within communities. Can be used to evaluate the efficacy of potential control strategies before attempting costly and/or risky field trials. – Simulations pointed out the difficulty of achieving success with quarantine measures alone.

Acknowledgements Collaborators and colleagues: Mc. Master University — Ann Herring, Dick Preston University of Manitoba — Rob Hoppa University of Missouri — Carrie Ahillen, Connie Carpenter, Nate Green, Suman Kanuganti, Melissa Stoops, Emily Williams Funding: The National Science Foundation The Canadian Social Sciences and Humanities Research Council Special thanks to the Norway House First Cree Nation who generously gave permission to work with their historical documents. Leonard Mc. Kay, in particular, was a constant source of encouragement and assistance.