Where do partitions come from informational Tho

Where do partitions come from? informational

Tho saugh I. . . alle the mervelous signals Of the goddys celestials Chaucer, The House of Fame (c 1384) . . . . States Signal = player’s information = player’s knowledge

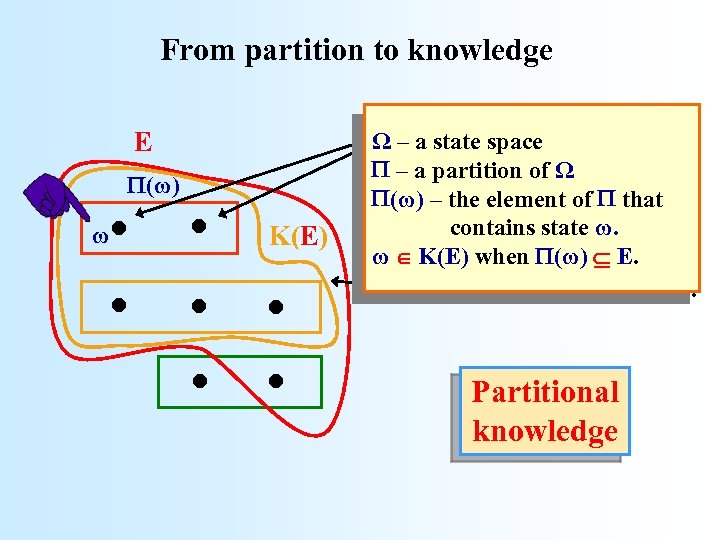From partition to knowledge E . . . . (ω) ω K(E) Here the player knows the Ω – element of the partition a state space – that contains the states. a partition of Ω (ω) – thealso E. of that. . . and element contains state ω. ω K(E) when (ω) E. The event that she knows E. Partitional knowledge

From knowledge to partition Syntax vs. Semantics Sentences Bob knows that G. W. Bush is the president of the US and he does not know that Barbara is G. W. ’s wife. Deduction rules A family of sets closed The set of all sentences form a Boolean algebra under intersection and (w. r. t “and”, “or”, “not”) with an operator (know) complement Language: An algebra of subsets, A with an operator K: A A.

From knowledge to partition The axioms of S 5 knowledge: 0. The axioms of Boolean algebra 1. K( ) = 2. K(E) K(F) = K(E F) 3. K(E) E 4. ¬ K(E) = K(¬ K(E))

British Panel Gives Rumsfeld 'Foot In Mouth' Award Defense Secretary's Comment On 'Known Unknowns' Is Most Baffling LONDON -- He may not know it -- or he may know that he knows it -- but Secretary of Defense Donald Rumsfeld has won this year's "Foot in Mouth" award for the most baffling statement by a public figure. Britain's Plain English Campaign cited Rumsfeld's comment on Iraq, when he said the following during a Pentagon briefing: "Reports that say that something hasn't happened are always interesting to me, because as we know, there are knowns , there are things we know. "We also know there are known unknowns. That is to say we know there are some things we do not know. But there also unknowns: the ones we don't know. ”

From knowledge to partition The axioms of S 5 knowledge: 0. The axioms of Boolean algebra 1. K( ) = 2. K(E) K(F) = K(E F) 3. K(E) E 4. ¬ K(E) = K(¬ K(E)) Partitional knowledge satisfies S 5. Is S 5 -knowledge partitional?

S 5 . Fairy tale: Hard facts: S 5 implies partition Words alone do not bring about partitions

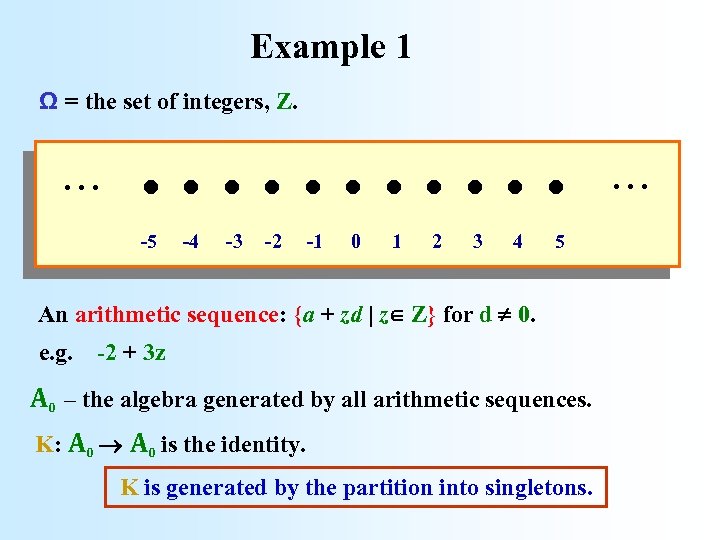Example 1 Ω = the set of integers, Z. . . . -5 -4 -3 -2 -1 0 1 2 3 4 5 An arithmetic sequence: {a + zd | z Z} for d 0. e. g. -2 + 3 z A 0 – the algebra generated by all arithmetic sequences. K: A 0 is the identity. K is generated by the partition into singletons. .

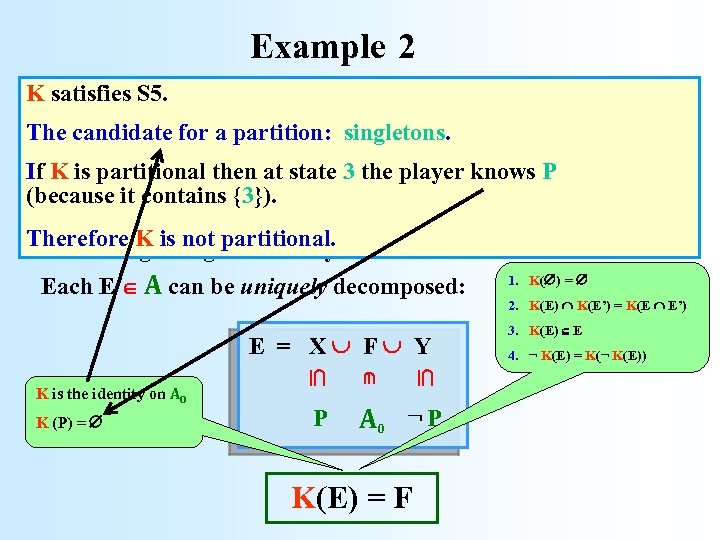Example 1 2 . . . K satisfies S 5. . . The. candidate for a partition: singletons. P . . . If K is partitional then at state 30 the 1 player knows P 5 -5 -4 -3 -2 -1 2 3 4 (because it contains {3}). Therefore K is not partitional. A and the set P. A – the algebra generated by 0 Each E A can be uniquely decomposed: E = X F Y P A 0 ¬ P K(E) = F K (P) = K is the identity on A 0 1. K( ) = 2. K(E) K(E’) = K(E E’) 3. K(E) E 4. ¬ K(E) = K(¬ K(E))

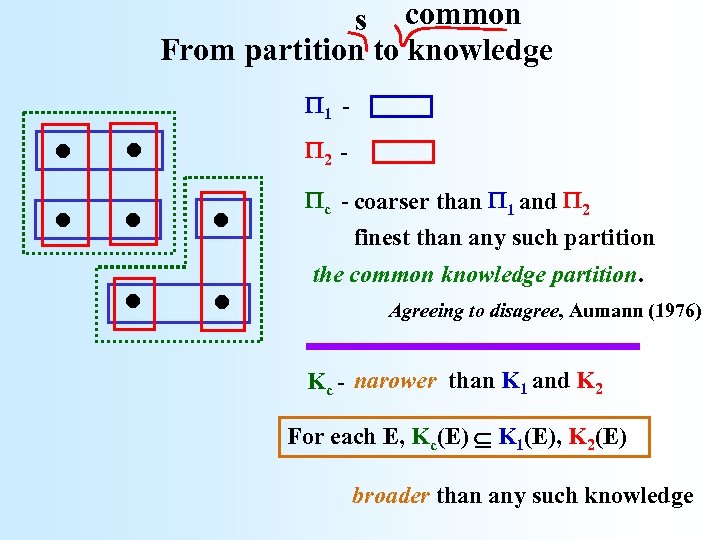s common From partition to knowledge . . . . 1 2 c - coarser than 1 and 2 finest than any such partition the common knowledge partition. Agreeing to disagree, Aumann (1976) Kc - narower than K 1 and K 2 For each E, Kc(E) K 1(E), K 2(E) broader than any such knowledge

s common From partition to knowledge 1 Is it possible to prove syntactically the existence of Kc for S 5 knowledge K 1 and K 2 ? 2 c - coarser than 1 and 2 finest than any such partition the common knowledge partition. Agreeing to disagree, Aumann (1976) NO! Kc - narower than K 1 and K 2 For each E, Kc(E) K 1(E), K 2(E) broader than any such knowledge

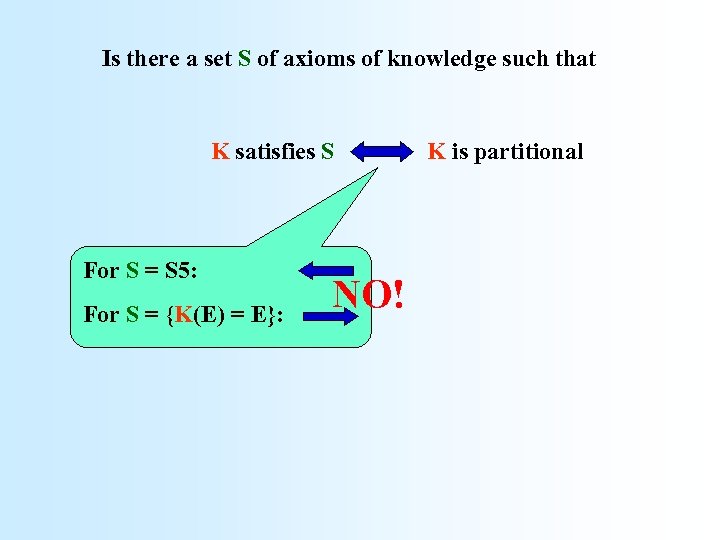Is there a set S of axioms of knowledge such that K satisfies S For S = S 5: For S = {K(E) = E}: NO! K is partitional