e6b4a20c3a11ca267ebd0bbfb9902775.ppt
- Количество слайдов: 94

What You See May Not Be What You Get: A Primer on Regression Artifacts Michael A. Babyak, Ph. D Duke University Medical Center


Topics to Cover 1. 2. 3. 4. 5. 6. 7. Models: what and why? Preliminaries—requirements for a good model Dichotomizing a graded or continuous variable is dumb Using degrees of freedom wisely Covariate selection Transformations and smoothing techniques for non-linear effects Resampling as a superior method of model validation

What is a model ? Y = f(x 1, x 2, x 3…xn) Y = a + b 1 x 1 + b 2 x 2…bnxn Y = e a + b 1 x 1 + b 2 x 2…bnxn

Why Model? (instead of test) 1. Can capture theoretical/predictive system 2. Estimates of population parameters 3. Allows prediction as well as hypothesis testing 4. More information for replication

Preliminaries 1. Correct model 2. Measure well and don’t throw information away 3. Adequate Sample Size

Correct Model • Gaussian: General Linear Model • Multiple linear regression • Binary (or ordinal): Generalized Linear Model • Logistic Regression • Proportional Odds/Ordinal Logistic • Time to event: • Cox Regression • Distribution of predictors generally not important

Measure well and don’t throw information away • Reliable, interpretable • Use all the information about the variables of interest • Don’t create “clinical cutpoints” before modeling • Model with ALL the data first, then use prediction to make decisions about cutpoints

Dichotomizing for Convenience Can Destroy a Model
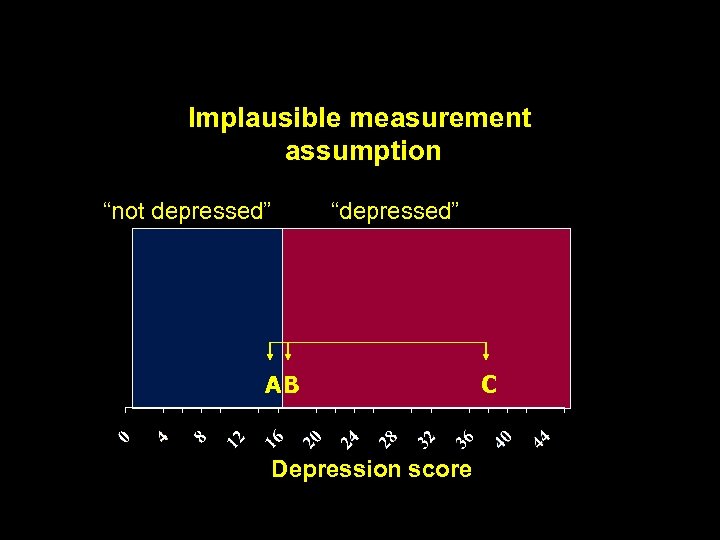
Implausible measurement assumption “not depressed” “depressed” AB Depression score C

Dichotomization, by definition, reduces power by a minimum of about 30% http: //psych. colorado. edu/~mcclella/Median. Split/

Dichotomization, by definition, reduces power by a minimum of about 30% Dear Project Officer, In order to facilitate analysis and interpretation, we have decided to throw away about 30% of our data. Even though this will waste about 3 or 4 hundred thousand dollars worth of subject recruitment and testing money, we are confident that you will understand. Sincerely, Dick O. Tomi, Ph. D Prof. Richard Obediah Tomi, Ph. D

Examples from the WCGS Study: Correlations with CHD Mortality (n = 750)

Dichotomizing does not reduce measurement error Gustafson, P. and Le, N. D. (2001). A comparison of continuous and discrete measurement error: is it wise to dichotomize imprecise covariates? Submitted. Available at http: //www. stat. ubc. ca/people/gustaf.

Simulation: Dichotomizing makes matters worse when measure is unreliable b 1 =. 4 X 1 Y True Model: X 1 continuous

Simulation: Dichotomizing makes matters worse when measure is unreliable b 1 =. 4 X 1 Y Same Model with X 1 dichotomized
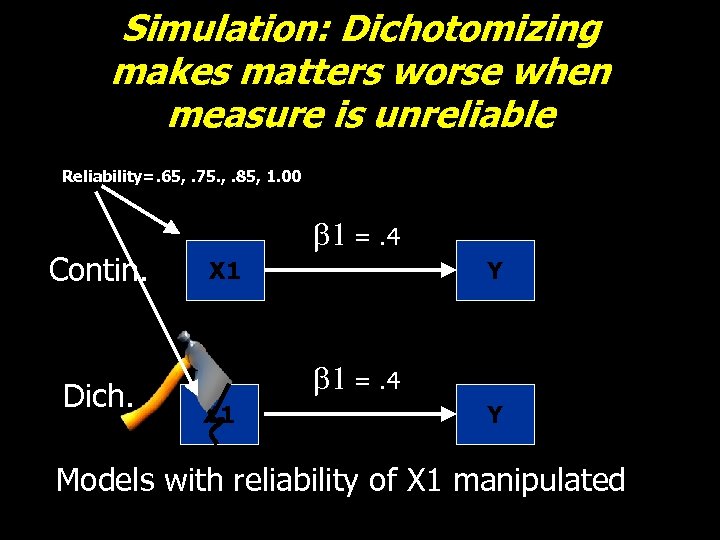
Simulation: Dichotomizing makes matters worse when measure is unreliable Reliability=. 65, . 75. , . 85, 1. 00 Contin. Dich. b 1 =. 4 X 1 Y Models with reliability of X 1 manipulated
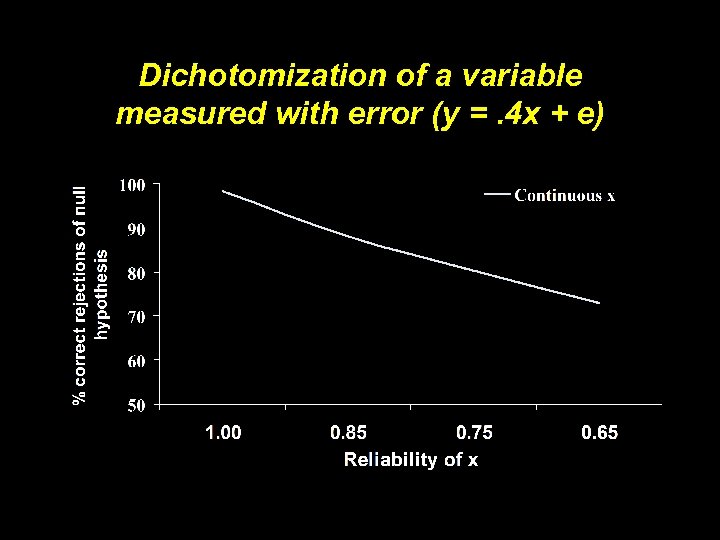
Dichotomization of a variable measured with error (y =. 4 x + e)
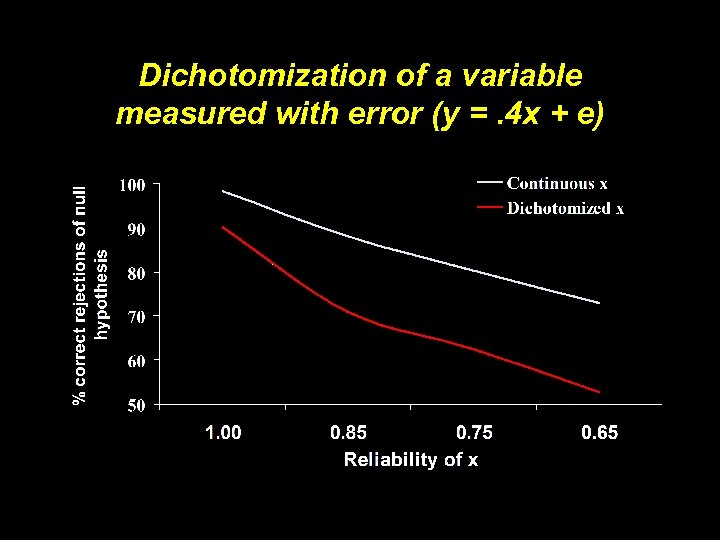
Dichotomization of a variable measured with error (y =. 4 x + e)
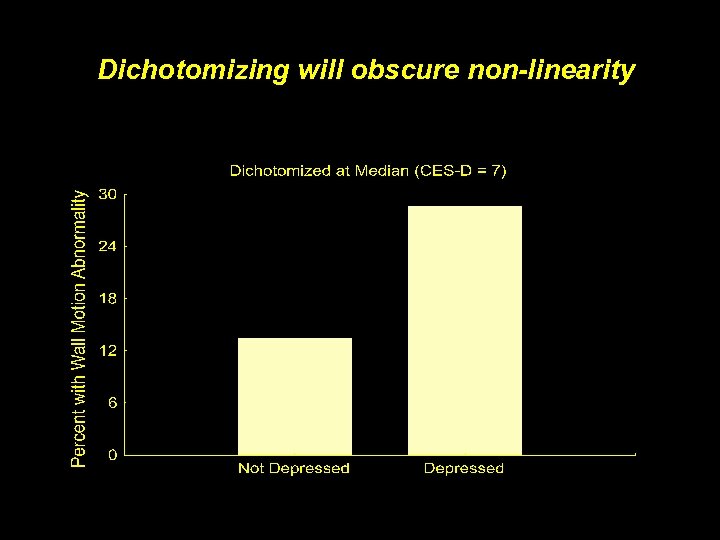
Dichotomizing will obscure non-linearity
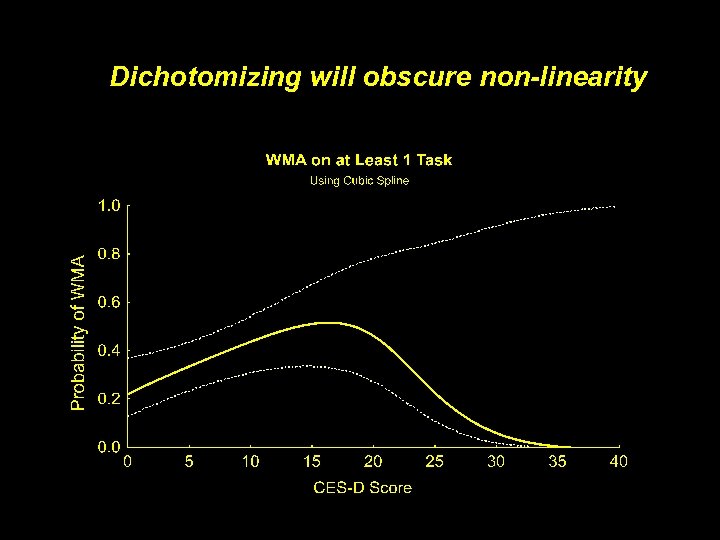
Dichotomizing will obscure non-linearity
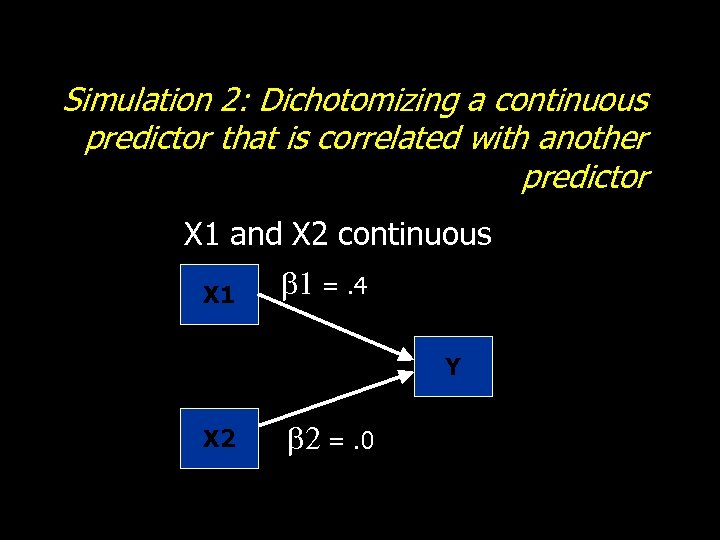
Simulation 2: Dichotomizing a continuous predictor that is correlated with another predictor X 1 and X 2 continuous X 1 b 1 =. 4 Y X 2 b 2 =. 0
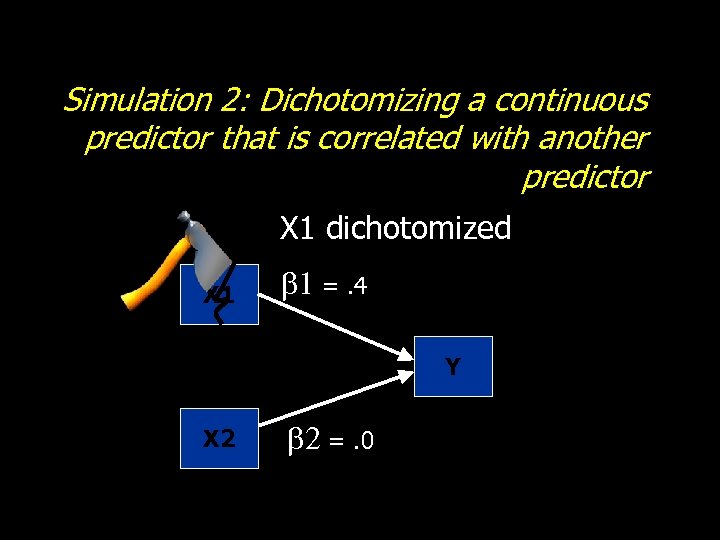
Simulation 2: Dichotomizing a continuous predictor that is correlated with another predictor X 1 dichotomized X 1 b 1 =. 4 Y X 2 b 2 =. 0
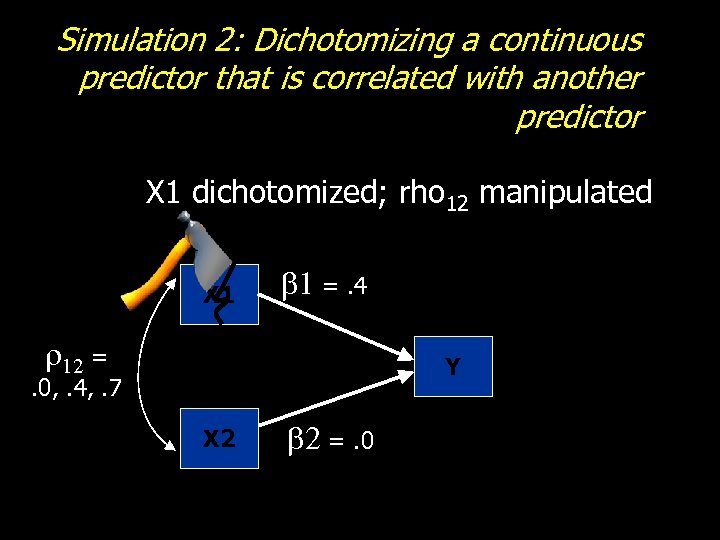
Simulation 2: Dichotomizing a continuous predictor that is correlated with another predictor X 1 dichotomized; rho 12 manipulated X 1 b 1 =. 4 r 12 = Y . 0, . 4, . 7 X 2 b 2 =. 0

Simulation 2: Dichotomizing a continuous predictor that is correlated with another predictor
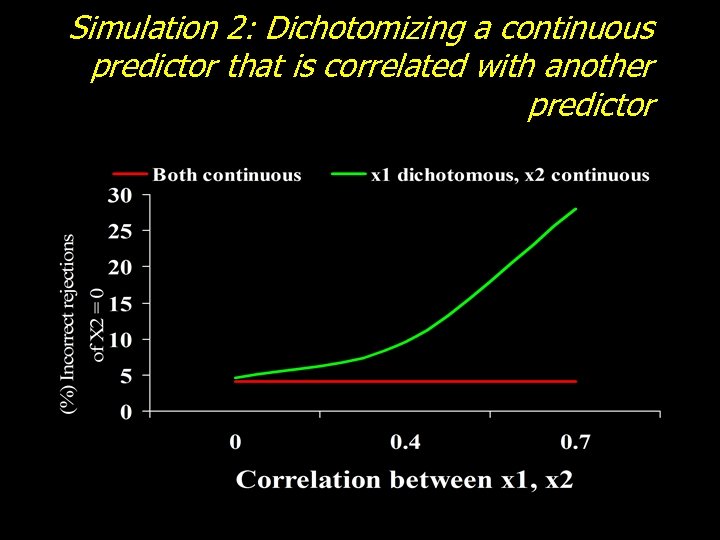
Simulation 2: Dichotomizing a continuous predictor that is correlated with another predictor

Is it ever a good idea to categorize quantitatively measured variables? • Yes: – when the variable is truly categorical – for descriptive/presentational purposes – for hypothesis testing, if enough categories are made. • However, using many categories can lead to problems of multiple significance tests and still run the risk of misclassification

CONCLUSIONS • Cutting: – Doesn’t always make measurement sense – Almost always reduces power – Can fool you with too much power in some instances – Can completely miss important features of the underlying function • Modern computing/statistical packages can “handle” continuous variables • Want to make good clinical cutpoints? Model first, cut later.
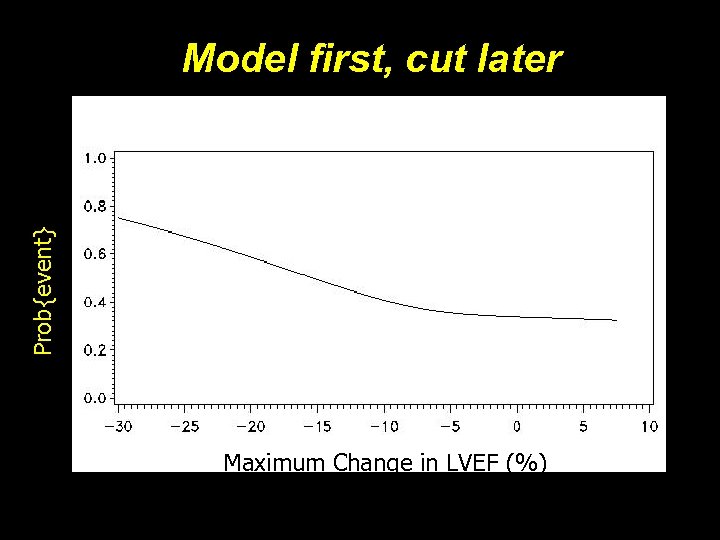
Clinical Events and LVEF Change during Mental Stress: 5 Year follow-up Prob{event} Model first, cut later Maximum Change in LVEF (%)

Requirements: Sample Size • Linear regression – minimum of N = 50 + 8: predictor (Green, 1990) • Logistic Regression – Minimum of N = 10 -15/predictor among smallest group (Peduzzi et al. , 1990 a) • Survival Analysis – Minimum of N = 10 -15/predictor (Peduzzi et al. , 1990 b)
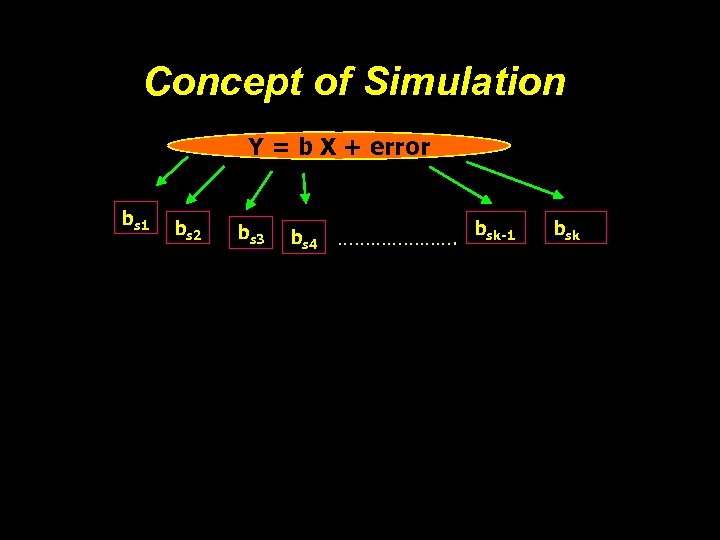
Concept of Simulation Y = b X + error bs 1 bs 2 bs 3 bs 4 …………………. bsk-1 bsk
Concept of Simulation Y = b X + error bs 1 bs 2 bs 3 bs 4 …………………. bsk-1 Evaluate bsk
Simulation Example Y =. 4 X + error bs 1 bs 2 bs 3 bs 4 …………………. bsk-1 bsk
Simulation Example Y =. 4 X + error bs 1 bs 2 bs 3 bs 4 …………………. bsk-1 Evaluate bsk
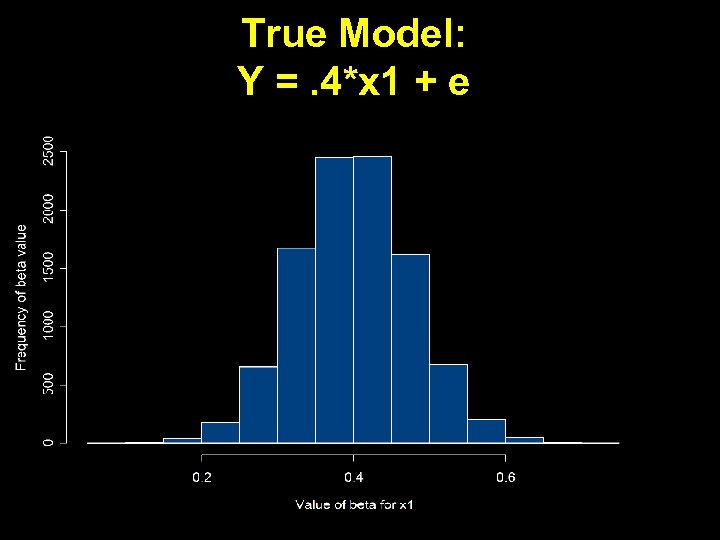
True Model: Y =. 4*x 1 + e

Sample Size • Linear regression – minimum of N = 50 + 8: predictor (Green, 1990) • Logistic Regression – Minimum of N = 10 -15/predictor among smallest group (Peduzzi et al. , 1990 a) • Survival Analysis – Minimum of N = 10 -15/predictor (Peduzzi et al. , 1990 b)
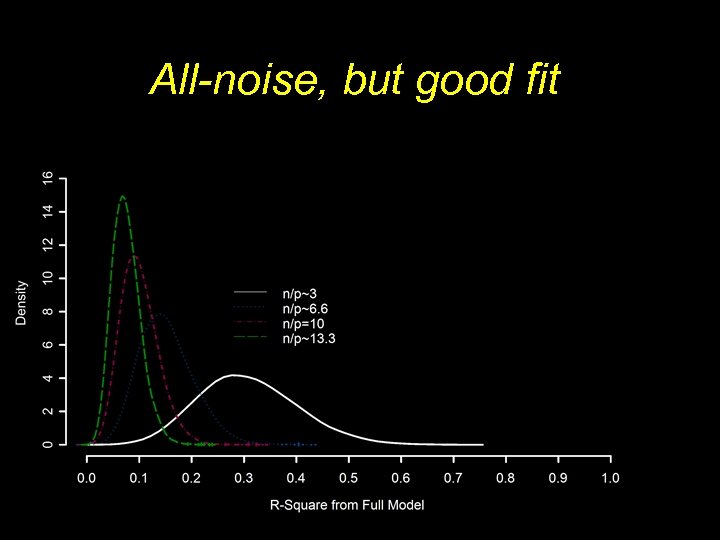
All-noise, but good fit

Simulation: number of events/predictor ratio Y =. 5*x 1 + 0*x 2 +. 2*x 3 + 0*x 4 -- Where r x 1 x 4 =. 4 -- N/p = 3, 5, 10, 20, 50
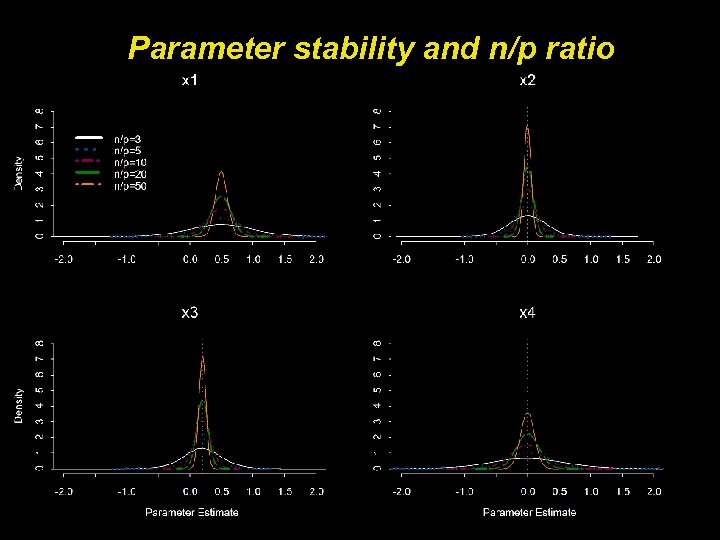
Parameter stability and n/p ratio

Peduzzi’s Simulation: number of events/predictor ratio P(survival) =a + b 1*NYHA + b 2*CHF + b 3*VES +b 4*DM + b 5*STD + b 6*HTN + b 7*LVC --Events/p = 2, 5, 10, 15, 20, 25 --% relative bias = (estimated b – true b/true b)*100
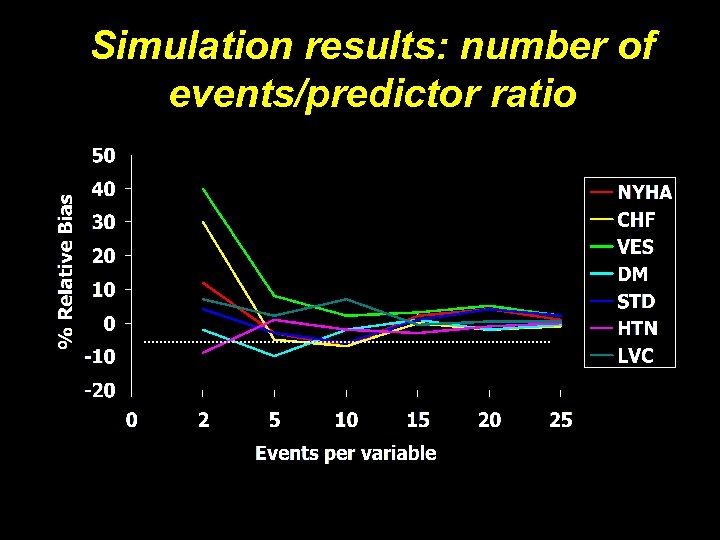
Simulation results: number of events/predictor ratio
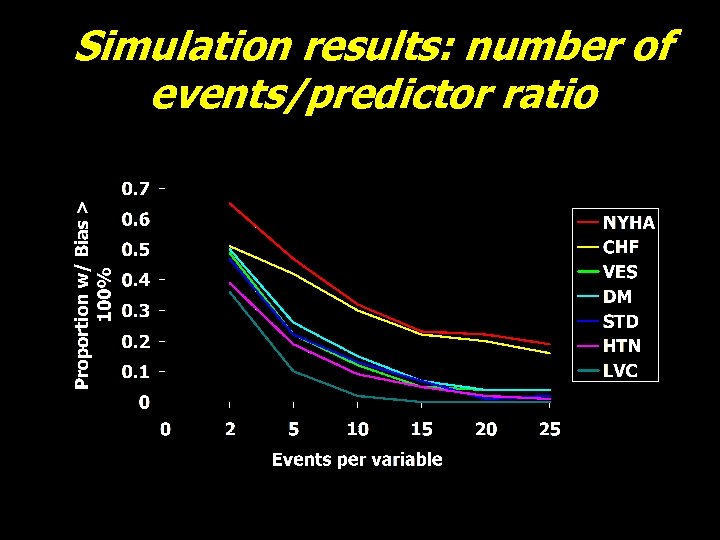
Simulation results: number of events/predictor ratio

Predictor (covariate) selection 1. 2. 3. 4. Theory, substantive knowledge, prior models Testing for confounding Univariate testing Last (and least), automated methods, aka stepwise and best subset regression

Searching for Confounders • Fundamental tension between underfitting and overfitting • Underfitting = not adjusting for important confounders • Overfitting = capitalizing on chance relations (sample fluctuation)

Covariate selection • Overfitting has been studied extensively • “Scariest” study is by Faraway (1992)— showed that any pre-modeling strategy cost a df over and above df used later in modeling. • Premodeling strategies included: variable selection, outlier detection, linearity tests, residual analysis.

Covariate selection • Therefore, if you transform, select, etc. , you must include the DF in (i. e. , penalize for) the “Final Model”

Covariate selection: Univariate Testing • Non-Significant tests also cost a DF • Variables may not behave the same way in a multivariable model—variable “not significant” at univariate test may be very important in the presence of other variables

Covariate selection • Despite the convention, testing for confounding has not been systematically studied—likely leads to overadjustment and underestimate of true effect of variable of interest. • At the very least, pulling variables in and out of models inflates the Type I error rate, sometimes dramatically

SOME of the problems with stepwise variable selection. 1. It yields R-squared values that are badly biased high

SOME of the problems with stepwise variable selection. 1. It yields R-squared values that are badly biased high 2. The F and chi-squared tests quoted next to each variable on the printout do not have the claimed distribution

SOME of the problems with stepwise variable selection. 1. It yields R-squared values that are badly biased high 2. The F and chi-squared tests quoted next to each variable on the printout do not have the claimed distribution 3. The method yields confidence intervals for effects and predicted values that are falsely narrow (See Altman and Anderson Stat in Med)

SOME of the problems with stepwise variable selection. 1. It yields R-squared values that are badly biased high 2. The F and chi-squared tests quoted next to each variable on the printout do not have the claimed distribution 3. The method yields confidence intervals for effects and predicted values that are falsely narrow (See Altman and Anderson Stat in Med) 4. It yields P-values that do not have the proper meaning and the proper correction for them is a very difficult problem

SOME of the problems with stepwise variable selection. 1. It yields R-squared values that are badly biased high 2. The F and chi-squared tests quoted next to each variable on the printout do not have the claimed distribution 3. The method yields confidence intervals for effects and predicted values that are falsely narrow (See Altman and Anderson Stat in Med) 4. It yields P-values that do not have the proper meaning and the proper correction for them is a very difficult problem 5. It gives biased regression coefficients that need shrinkage (the coefficients for remaining variables are too large; see Tibshirani, 1996)

SOME of the problems with stepwise variable selection. 1. It yields R-squared values that are badly biased high 2. The F and chi-squared tests quoted next to each variable on the printout do not have the claimed distribution 3. The method yields confidence intervals for effects and predicted values that are falsely narrow (See Altman and Anderson Stat in Med) 4. It yields P-values that do not have the proper meaning and the proper correction for them is a very difficult problem 5. It gives biased regression coefficients that need shrinkage (the coefficients for remaining variables are too large; see Tibshirani, 1996). 6. It has severe problems in the presence of collinearity

SOME of the problems with stepwise variable selection. 1. It yields R-squared values that are badly biased high 2. The F and chi-squared tests quoted next to each variable on the printout do not have the claimed distribution 3. The method yields confidence intervals for effects and predicted values that are falsely narrow (See Altman and Anderson Stat in Med) 4. It yields P-values that do not have the proper meaning and the proper correction for them is a very difficult problem 5. It gives biased regression coefficients that need shrinkage (the coefficients for remaining variables are too large; see Tibshirani, 1996). 6. It has severe problems in the presence of collinearity 7. It is based on methods (e. g. F- tests for nested models) that were intended to be used to test pre-specified hypotheses

SOME of the problems with stepwise variable selection. 1. It yields R-squared values that are badly biased high 2. The F and chi-squared tests quoted next to each variable on the printout do not have the claimed distribution 3. The method yields confidence intervals for effects and predicted values that are falsely narrow (See Altman and Anderson Stat in Med) 4. It yields P-values that do not have the proper meaning and the proper correction for them is a very difficult problem 5. It gives biased regression coefficients that need shrinkage (the coefficients for remaining variables are too large; see Tibshirani, 1996). 6. It has severe problems in the presence of collinearity 7. It is based on methods (e. g. F tests for nested models) that were intended to be used to test pre-specified hypotheses. 8. Increasing the sample size doesn't help very much (see Derksen and Keselman)

SOME of the problems with stepwise variable selection. 1. It yields R-squared values that are badly biased high 2. The F and chi-squared tests quoted next to each variable on the printout do not have the claimed distribution 3. The method yields confidence intervals for effects and predicted values that are falsely narrow (See Altman and Anderson Stat in Med) 4. It yields P-values that do not have the proper meaning and the proper correction for them is a very difficult problem 5. It gives biased regression coefficients that need shrinkage (the coefficients for remaining variables are too large; see Tibshirani, 1996). 6. It has severe problems in the presence of collinearity 7. It is based on methods (e. g. F tests for nested models) that were intended to be used to test pre-specified hypotheses. 8. Increasing the sample size doesn't help very much (see Derksen and Keselman) 9. It allows us to not think about the problem

SOME of the problems with stepwise variable selection. 1. It yields R-squared values that are badly biased high 2. The F and chi-squared tests quoted next to each variable on the printout do not have the claimed distribution 3. The method yields confidence intervals for effects and predicted values that are falsely narrow (See Altman and Anderson Stat in Med) 4. It yields P-values that do not have the proper meaning and the proper correction for them is a very difficult problem 5. It gives biased regression coefficients that need shrinkage (the coefficients for remaining variables are too large; see Tibshirani, 1996). 6. It has severe problems in the presence of collinearity 7. It is based on methods (e. g. F tests for nested models) that were intended to be used to test pre-specified hypotheses. 8. Increasing the sample size doesn't help very much (see Derksen and Keselman) 9. It allows us to not think about the problem 10. It uses a lot of paper

“I now wish I had never written the stepwise selection code for SAS. ” --Frank Harrell, author of forward and backwards selection algorithm for SAS PROC REG

Automated Selection: Derksen and Keselman (1992) Simulation Study • Studied backward and forward selection • Some authentic variables and some noise variables among candidate variables • Manipulated correlation among candidate predictors • Manipulated sample size

Automated Selection: Derksen and Keselman (1992) Simulation Study • “The degree of correlation between candidate predictors affected the frequency with which the authentic predictors found their way into the model. ” • “The greater the number of candidate predictors, the greater the number of noise variables were included in the model. ” • “Sample size was of little practical importance in determining the number of authentic variables contained in the final model. ”
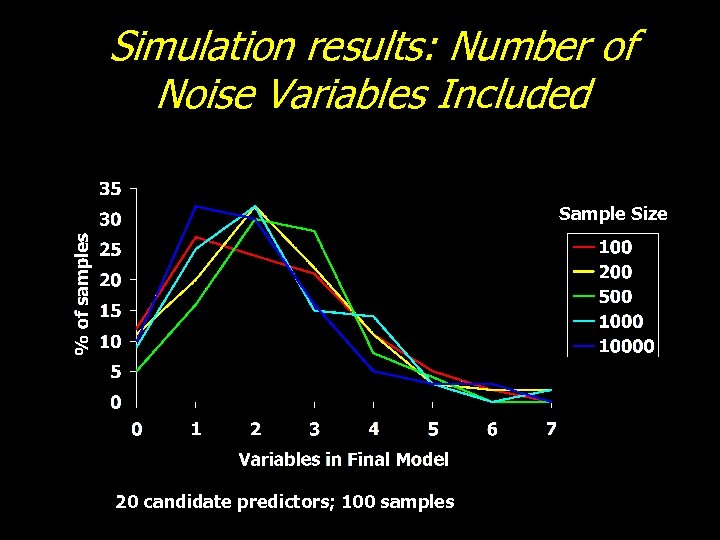
Simulation results: Number of Noise Variables Included Sample Size 20 candidate predictors; 100 samples
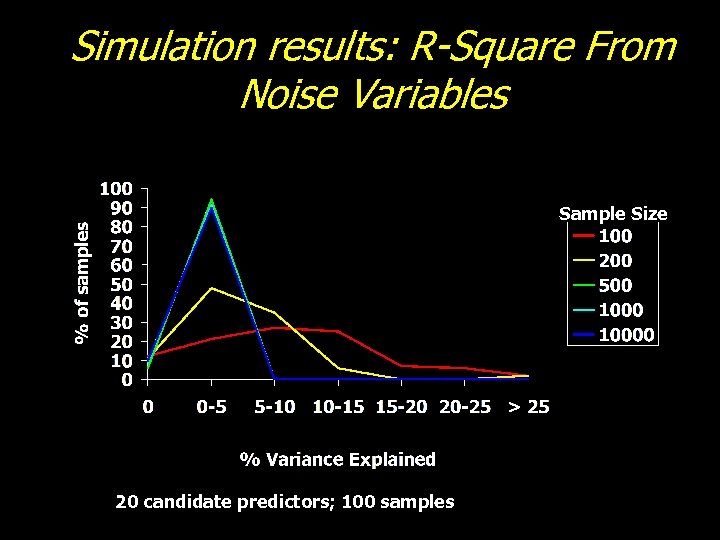
Simulation results: R-Square From Noise Variables Sample Size 20 candidate predictors; 100 samples
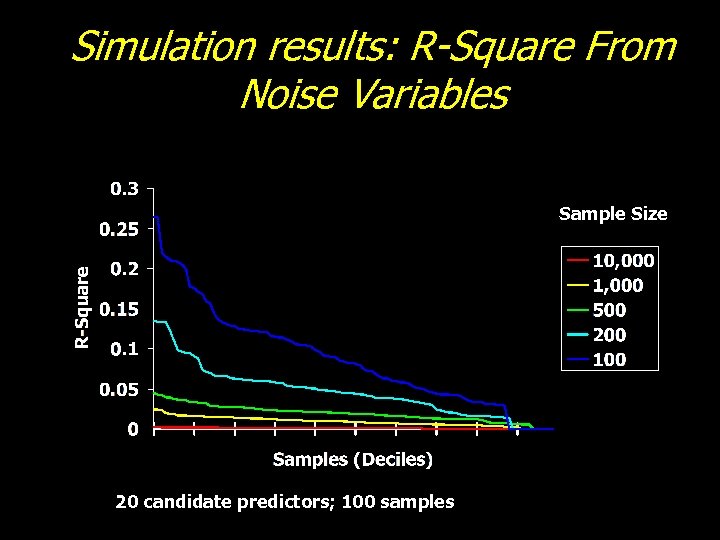
Simulation results: R-Square From Noise Variables Sample Size 20 candidate predictors; 100 samples

Variable Selection • Pick variables a priori • Stick with them • Penalize appropriately for any datadriven decision about how to model a variable

Spending DF wisely • Select variables of most importance • Use DF to assess non-linearity using flexible curve approach (more about this later) • If not enough N/predictor, combine covariates using techniques that do not look at Y in the sample, PCA, FA, conceptual clustering, collapsing, scoring, established indexes, propensity scores.

Can use data to determine where to spend DF • Use Spearman’s Rho to test “importance” • Not peeking because we have chosen to include the term in the model regardless of relation to Y • Use more DF for non-linearity

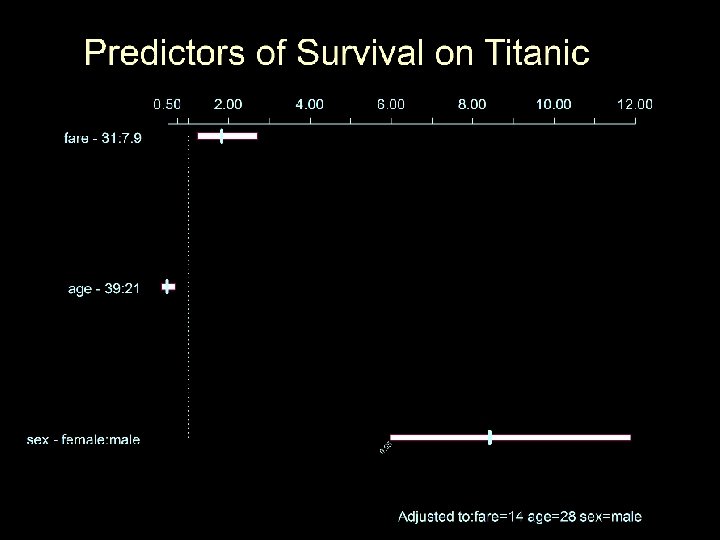
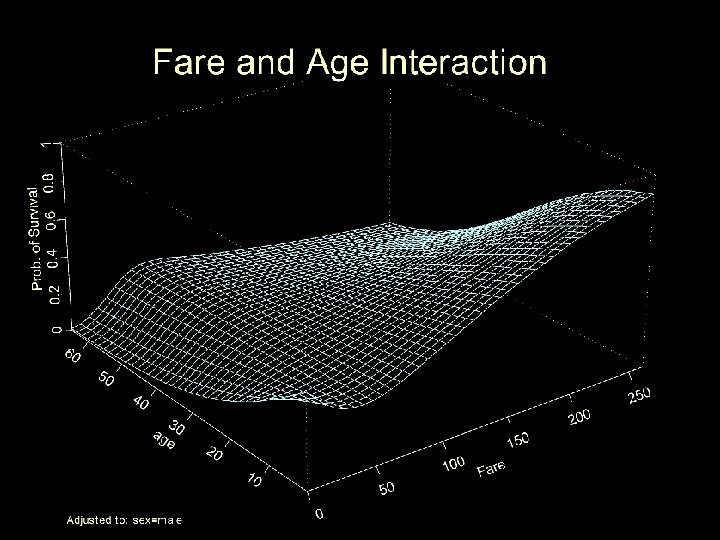
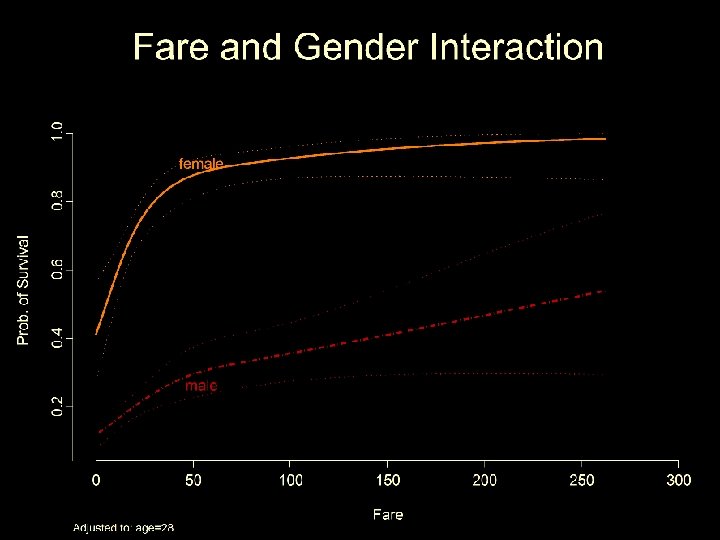
Example-Predict Survival from age, gender, and fare on Titanic

If you have already decided to include them (and promise to keep them in the model) you can peek at predictors in order to see where to add complexity
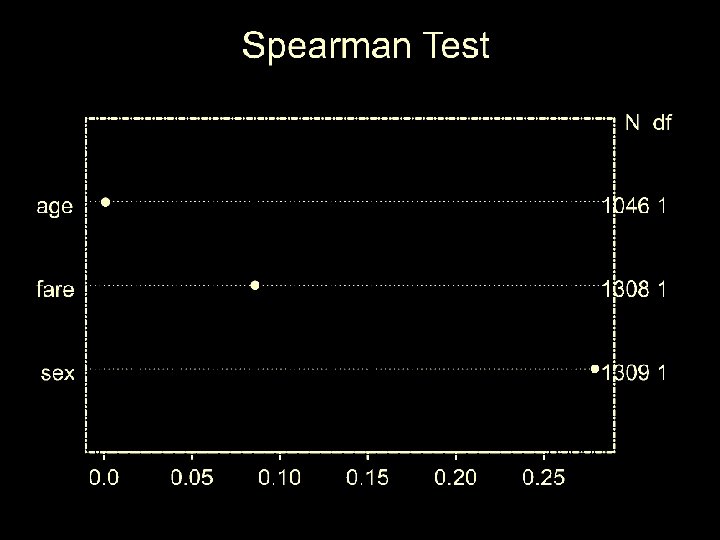

Non-linearity using splines
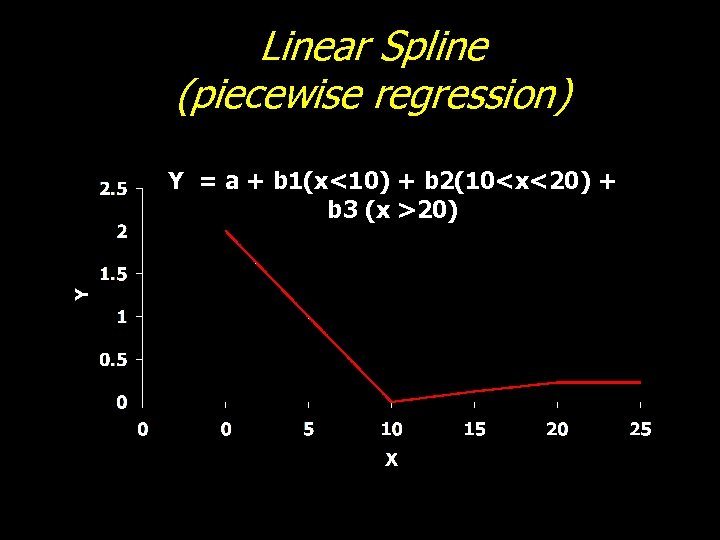
Linear Spline (piecewise regression) Y = a + b 1(x<10) + b 2(10<x<20) + b 3 (x >20)
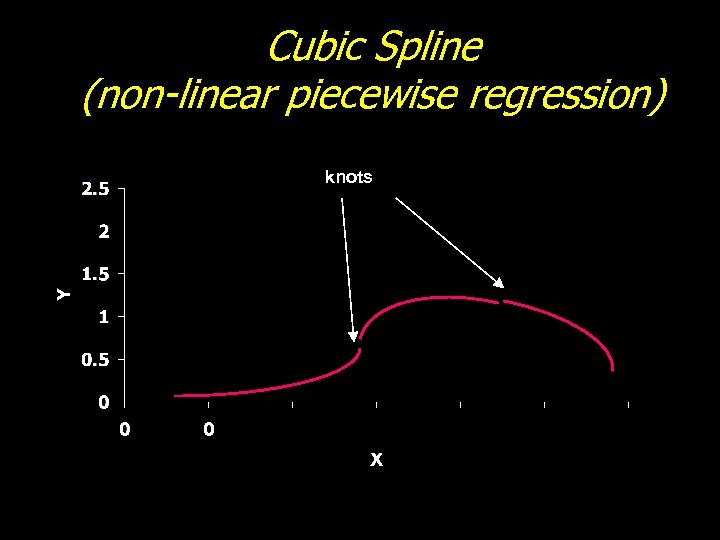
Cubic Spline (non-linear piecewise regression) knots
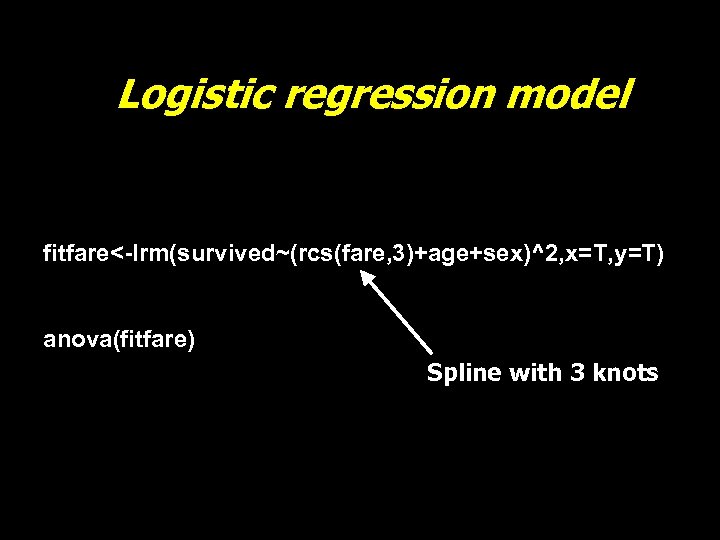
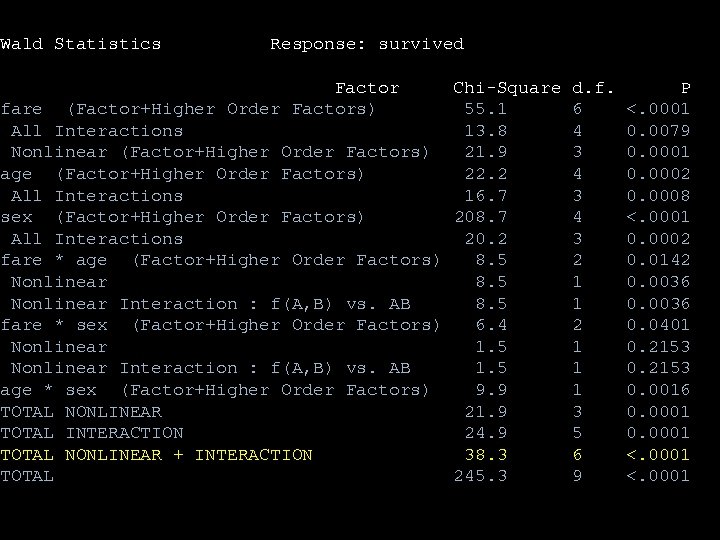
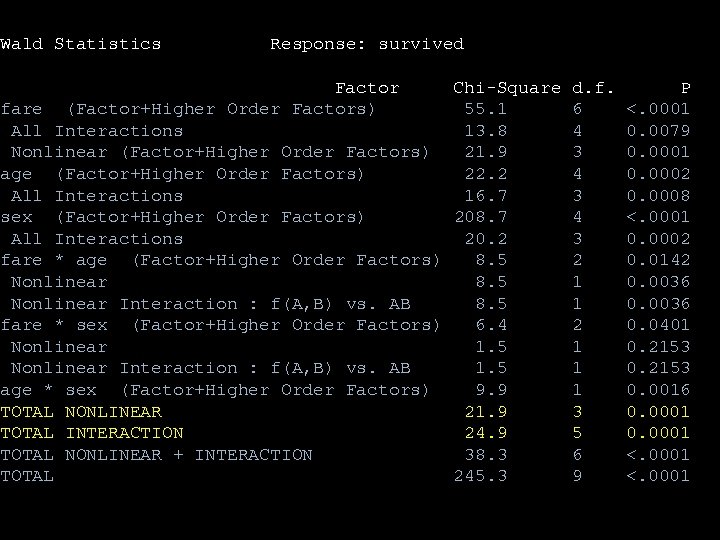
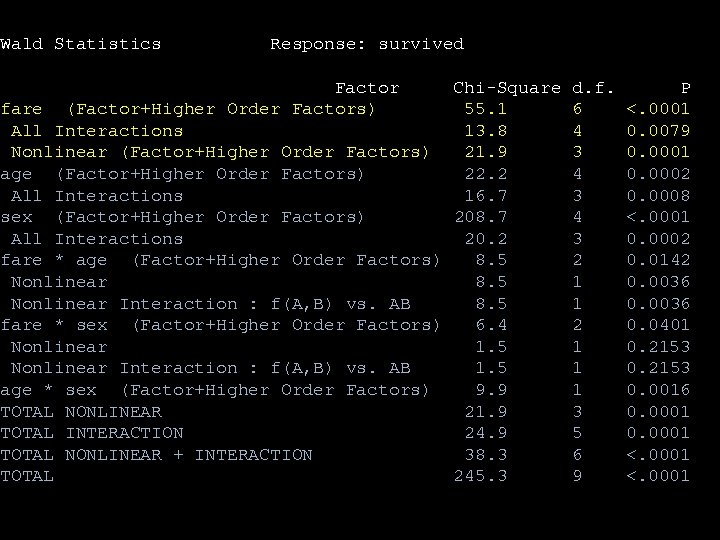
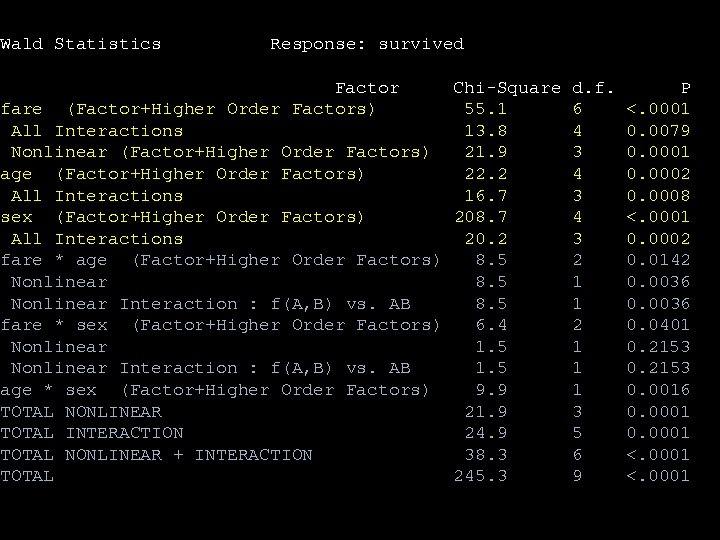
Logistic regression model fitfare<-lrm(survived~(rcs(fare, 3)+age+sex)^2, x=T, y=T) anova(fitfare) Spline with 3 knots
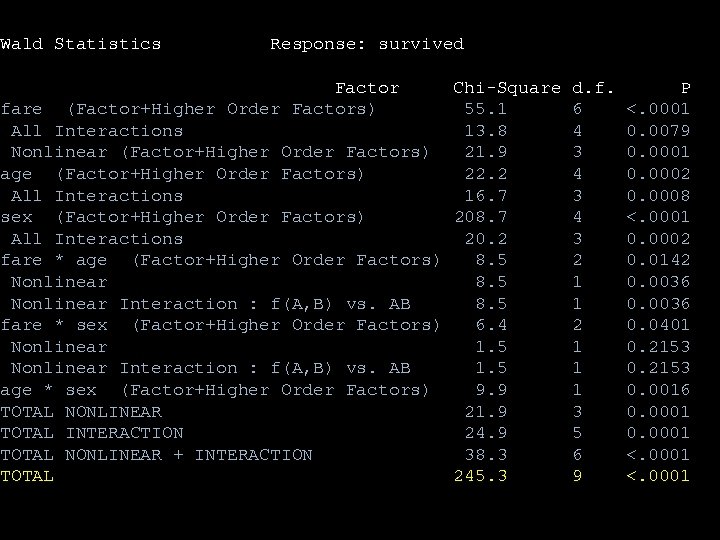
Wald Statistics Response: survived Factor Chi-Square d. f. fare (Factor+Higher Order Factors) 55. 1 6 All Interactions 13. 8 4 Nonlinear (Factor+Higher Order Factors) 21. 9 3 age (Factor+Higher Order Factors) 22. 2 4 All Interactions 16. 7 3 sex (Factor+Higher Order Factors) 208. 7 4 All Interactions 20. 2 3 fare * age (Factor+Higher Order Factors) 8. 5 2 Nonlinear 8. 5 1 Nonlinear Interaction : f(A, B) vs. AB 8. 5 1 fare * sex (Factor+Higher Order Factors) 6. 4 2 Nonlinear 1. 5 1 Nonlinear Interaction : f(A, B) vs. AB 1. 5 1 age * sex (Factor+Higher Order Factors) 9. 9 1 TOTAL NONLINEAR 21. 9 3 TOTAL INTERACTION 24. 9 5 TOTAL NONLINEAR + INTERACTION 38. 3 6 TOTAL 245. 3 9 P <. 0001 0. 0079 0. 0001 0. 0002 0. 0008 <. 0001 0. 0002 0. 0142 0. 0036 0. 0401 0. 2153 0. 0016 0. 0001 <. 0001
Wald Statistics Response: survived Factor Chi-Square d. f. fare (Factor+Higher Order Factors) 55. 1 6 All Interactions 13. 8 4 Nonlinear (Factor+Higher Order Factors) 21. 9 3 age (Factor+Higher Order Factors) 22. 2 4 All Interactions 16. 7 3 sex (Factor+Higher Order Factors) 208. 7 4 All Interactions 20. 2 3 fare * age (Factor+Higher Order Factors) 8. 5 2 Nonlinear 8. 5 1 Nonlinear Interaction : f(A, B) vs. AB 8. 5 1 fare * sex (Factor+Higher Order Factors) 6. 4 2 Nonlinear 1. 5 1 Nonlinear Interaction : f(A, B) vs. AB 1. 5 1 age * sex (Factor+Higher Order Factors) 9. 9 1 TOTAL NONLINEAR 21. 9 3 TOTAL INTERACTION 24. 9 5 TOTAL NONLINEAR + INTERACTION 38. 3 6 TOTAL 245. 3 9 P <. 0001 0. 0079 0. 0001 0. 0002 0. 0008 <. 0001 0. 0002 0. 0142 0. 0036 0. 0401 0. 2153 0. 0016 0. 0001 <. 0001
Wald Statistics Response: survived Factor Chi-Square d. f. fare (Factor+Higher Order Factors) 55. 1 6 All Interactions 13. 8 4 Nonlinear (Factor+Higher Order Factors) 21. 9 3 age (Factor+Higher Order Factors) 22. 2 4 All Interactions 16. 7 3 sex (Factor+Higher Order Factors) 208. 7 4 All Interactions 20. 2 3 fare * age (Factor+Higher Order Factors) 8. 5 2 Nonlinear 8. 5 1 Nonlinear Interaction : f(A, B) vs. AB 8. 5 1 fare * sex (Factor+Higher Order Factors) 6. 4 2 Nonlinear 1. 5 1 Nonlinear Interaction : f(A, B) vs. AB 1. 5 1 age * sex (Factor+Higher Order Factors) 9. 9 1 TOTAL NONLINEAR 21. 9 3 TOTAL INTERACTION 24. 9 5 TOTAL NONLINEAR + INTERACTION 38. 3 6 TOTAL 245. 3 9 P <. 0001 0. 0079 0. 0001 0. 0002 0. 0008 <. 0001 0. 0002 0. 0142 0. 0036 0. 0401 0. 2153 0. 0016 0. 0001 <. 0001
Wald Statistics Response: survived Factor Chi-Square d. f. fare (Factor+Higher Order Factors) 55. 1 6 All Interactions 13. 8 4 Nonlinear (Factor+Higher Order Factors) 21. 9 3 age (Factor+Higher Order Factors) 22. 2 4 All Interactions 16. 7 3 sex (Factor+Higher Order Factors) 208. 7 4 All Interactions 20. 2 3 fare * age (Factor+Higher Order Factors) 8. 5 2 Nonlinear 8. 5 1 Nonlinear Interaction : f(A, B) vs. AB 8. 5 1 fare * sex (Factor+Higher Order Factors) 6. 4 2 Nonlinear 1. 5 1 Nonlinear Interaction : f(A, B) vs. AB 1. 5 1 age * sex (Factor+Higher Order Factors) 9. 9 1 TOTAL NONLINEAR 21. 9 3 TOTAL INTERACTION 24. 9 5 TOTAL NONLINEAR + INTERACTION 38. 3 6 TOTAL 245. 3 9 P <. 0001 0. 0079 0. 0001 0. 0002 0. 0008 <. 0001 0. 0002 0. 0142 0. 0036 0. 0401 0. 2153 0. 0016 0. 0001 <. 0001
Wald Statistics Response: survived Factor Chi-Square d. f. fare (Factor+Higher Order Factors) 55. 1 6 All Interactions 13. 8 4 Nonlinear (Factor+Higher Order Factors) 21. 9 3 age (Factor+Higher Order Factors) 22. 2 4 All Interactions 16. 7 3 sex (Factor+Higher Order Factors) 208. 7 4 All Interactions 20. 2 3 fare * age (Factor+Higher Order Factors) 8. 5 2 Nonlinear 8. 5 1 Nonlinear Interaction : f(A, B) vs. AB 8. 5 1 fare * sex (Factor+Higher Order Factors) 6. 4 2 Nonlinear 1. 5 1 Nonlinear Interaction : f(A, B) vs. AB 1. 5 1 age * sex (Factor+Higher Order Factors) 9. 9 1 TOTAL NONLINEAR 21. 9 3 TOTAL INTERACTION 24. 9 5 TOTAL NONLINEAR + INTERACTION 38. 3 6 TOTAL 245. 3 9 P <. 0001 0. 0079 0. 0001 0. 0002 0. 0008 <. 0001 0. 0002 0. 0142 0. 0036 0. 0401 0. 2153 0. 0016 0. 0001 <. 0001

Validation • Apparent • too optimistic • Internal • cross-validation, bootstrap • honest estimate for model performance • provides an upper limit to what would be found on external validation • External validation • replication with new sample, different circumstances

Validation • Steyerburg, et al. (1999) compared validation methods • Found that split-half was far too conservative • Bootstrap was equal or superior to all other techniques
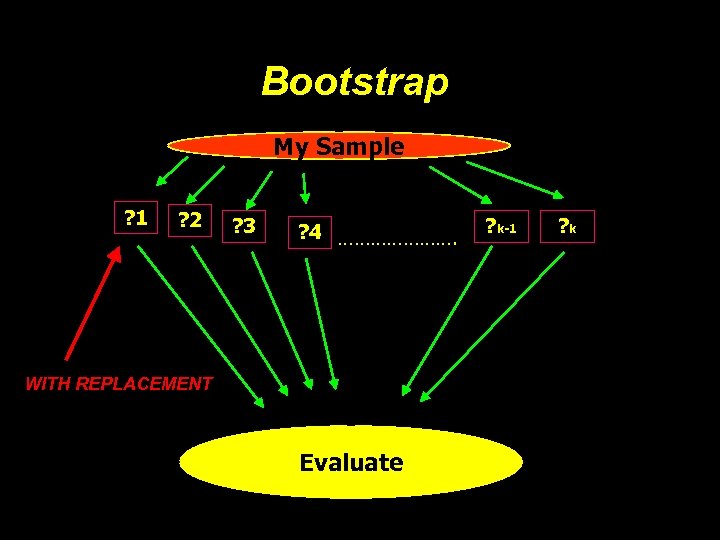
Bootstrap My Sample ? 1 ? 2 ? 3 ? 4 …………………. WITH REPLACEMENT Evaluate ? k-1 ? k
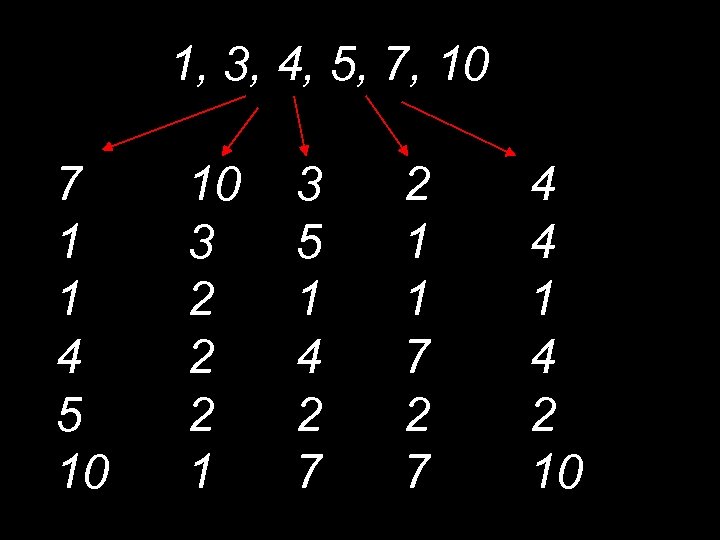
1, 3, 4, 5, 7, 10 7 1 1 4 5 10 10 3 2 2 2 1 3 5 1 4 2 7 2 1 1 7 2 7 4 4 1 4 2 10
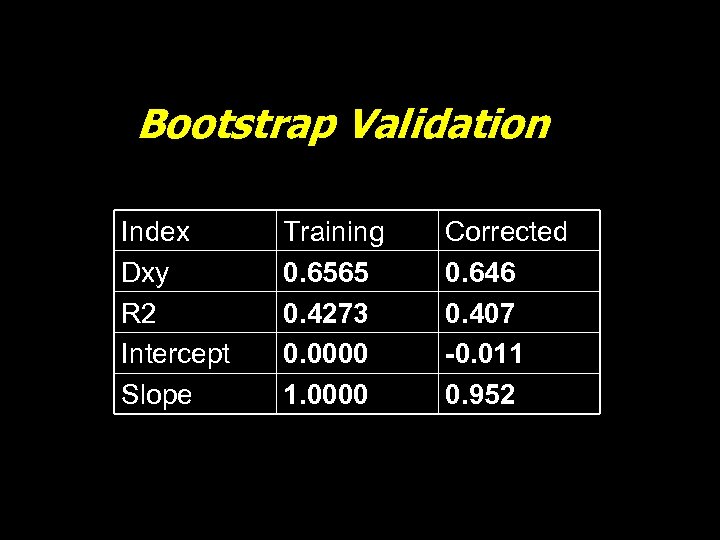
Bootstrap Validation Index Dxy R 2 Intercept Slope Training 0. 6565 0. 4273 0. 0000 1. 0000 Corrected 0. 646 0. 407 -0. 011 0. 952

Summary • Think about your model • Collect enough data

Summary • Measure well • Don’t destroy what you’ve measured

Summary • Pick your variables ahead of time and collect enough data to test the model you want • Keep all your variables in the model unless extremely unimportant

Summary • Use more df on important variables, fewer df on “nuisance” variables • Don’t peek at Y to combine, discard, or transform variables

Summary • Estimate validity and shrinkage with bootstrap

Summary • By all means, tinker with the model later, but be aware of the costs of tinkering • Don’t forget to say you tinkered • Go collect more data

Web links for references, software, and more • Harrell’s regression modeling text – http: //hesweb 1. med. virginia. edu/biostat/rms/ • SAS Macros for spline estimation – http: //hesweb 1. med. virginia. edu/biostat/SAS/survrisk. txt • Some results comparing validation methods – http: //hesweb 1. med. virginia. edu/biostat/reports/logistic. val. pdf • SAS code for bootstrap – ftp: //ftp. sas. com/pub/neural/jackboot. sas • S-Plus home page – insightful. com • Mike Babyak’s e-mail – michael. babyak@duke. edu • This presentation – http: //www. duke. edu/~mbabyak
e6b4a20c3a11ca267ebd0bbfb9902775.ppt