What is inclining experiment The inclining experiment is

What is inclining experiment The inclining experiment is a method of determining the vertical position of a vessel’s center of gravity, KG, usually for the light ship.

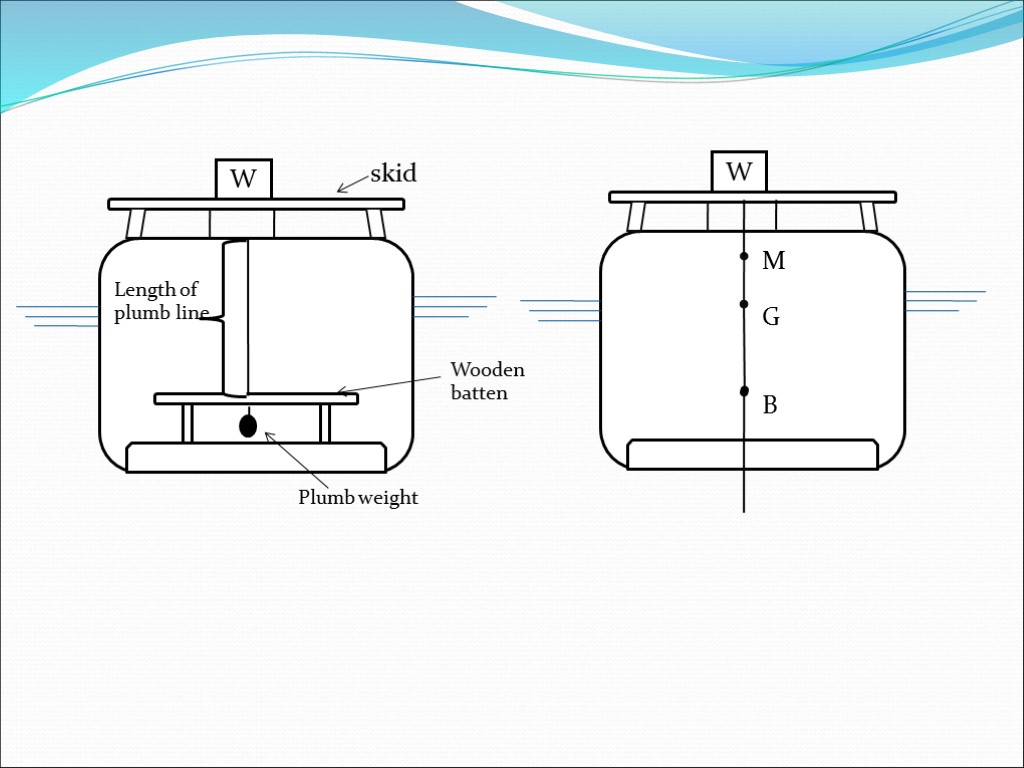
Required gear and data 1. A weight large enough to list the vessel 2⁰ to 3⁰ when moved across the deck 2. A method to move the weight across the vessel. 3. A plumb line suspended from the hatch cover to the lower hold. 4. A wooden batten placed horizontally across the ship lower hold. 5. The displacement of the vessel must be accurately known. 6. The value of KM for the displacement at the time of inclining experiment as determined from the hydrostatic data for the ship

Performing the inclining experiment Formula : GM = (w x d)/(displacement)(tanθ) w = the weight moved in tons d = the distance the weight moved in feet displacement = the vessel’s displacement in tons Tanθ = the tangent function of angle of inclination

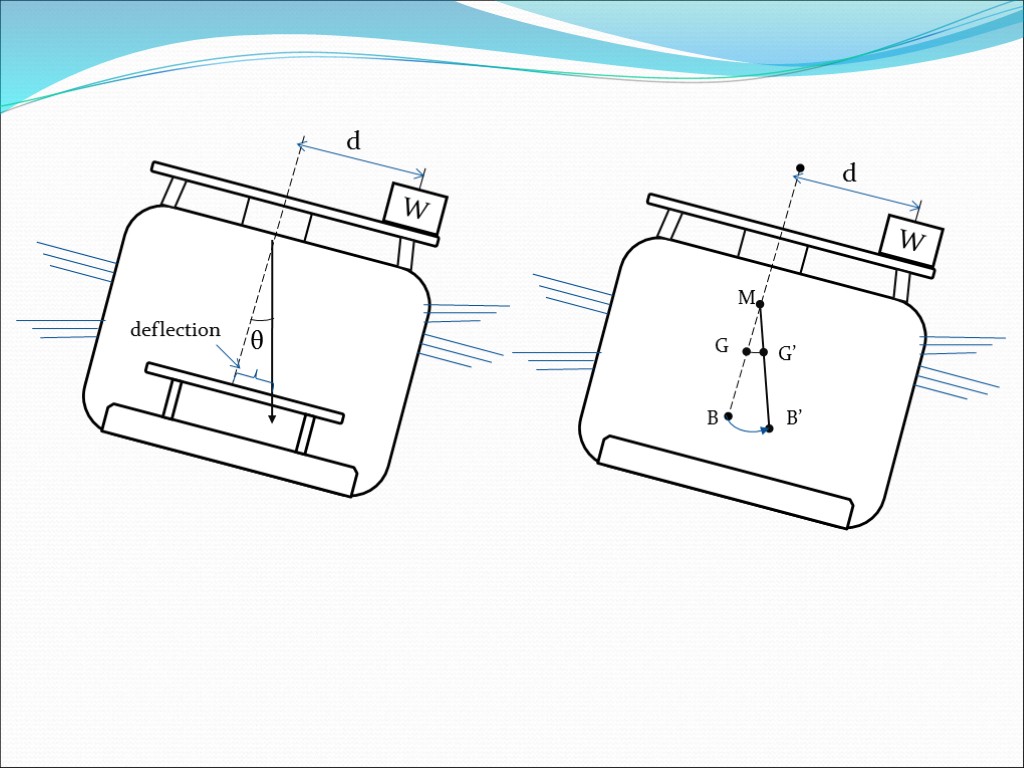
Derivation of inclining experiment formula In any weight is shifted onboard a vessel, the center of gravity of the vessel will shift in a direction parallel to the weight movement. The distance is found by formulas: GG’ = (w x d)/displacement Tanθ = GG’/GM GG’ = GMtanθ

Precautions to take during experiment 1. All tanks should be either full or empty. 2. All weights that might be boarded must be known. 3. The vessel should not have a list at the start of the experiment. 4. A calm day should be chosen 5. Soundings should be taken to ensure that there is adequate water depth to float the vessel 6. Members of crews should be sent ashore and during all readings, everyone aboard should be on the centerline.

7. The inclining weight must be shifted horizontally. 8. Averaging the result for accuracy.

Example 1 A ship is inclined by moving a weight of 20 tons a distance of 25 feet from the centerline. A 30-foot pendulum shows a deflection of 13 inches. Displacement of the ship is 3,700 tons. If the KM is 27.87 feet, what is the KG? tanθ = deflection of pendulum/length of pendulum KG = KM – KG = 27.87 – 3.74 feet= 24.13 feet

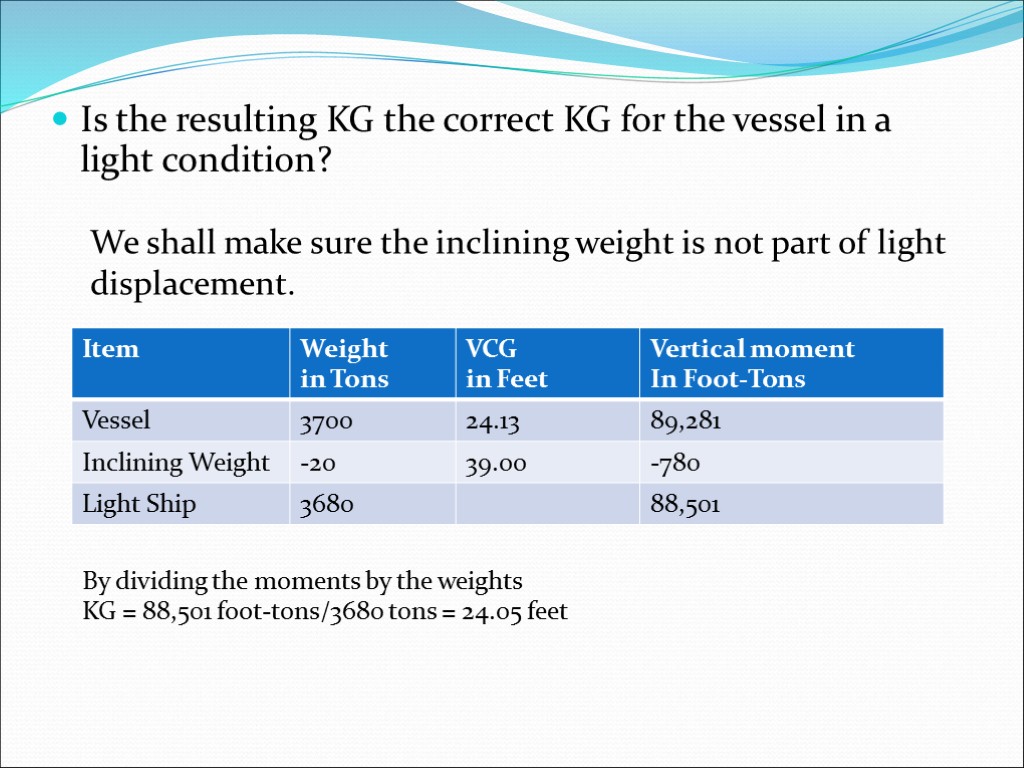
Is the resulting KG the correct KG for the vessel in a light condition? We shall make sure the inclining weight is not part of light displacement. By dividing the moments by the weights KG = 88,501 foot-tons/3680 tons = 24.05 feet

Practical applications 1. To find the angle of list, θ, a vessel will take by moving a weight transversely a distance, d tan θ = (w x d)/GM(displacement) θ = arc tan［(w x d)］/(GM)(displacement) 2. To find the weight, w, necessary to remove or produce a list by moving it a transverse distance d. w= (GM x tan θ x displacement)/d 3. To find the distance necessary to move a weight in order to remove or produce a heel d = (GM x tan θ x displacement)/w

Example1 A vessel is preparing to enter a dry dock and has a 4⁰ list to port. The displacement of the vessel is 6,150 tons with a GM of 3.7 feet. How many tons of ballast must be pumped from the port double bottoms to the starboard double bottoms to remove the list? The horizontal distance between the centers of gravity of these tanks is 30 feet. w = (GM x tanθ x displacement)/d W = (3.7 feet x 0.06993 x 6,150 tons)/30 feet = 53.0 tons

Example 2 How much of a list will a vessel of 12,000 tons take after a weight of 200 tons is shifted 40 feet across the deck? GM is 2 feet. Tan θ = (w x d)/(GM)(displacment) tan θ = (200 tons x 40 feet)/(2 feet)(12,000 tons)= 0.333 Θ = arc tan (0.333) = 18.42⁰

Example 3 What distance will a weight of 150 tons have to be moved in order to remove a 2⁰ list from a vessel? Displacement is 9,000 tons and GM is 3.4 feet. d = (GM x tan θ x displacement)/w d = (3.4 feet x 0.03492 x 9,000)/150 tons D= 7.1 feet

The moment to heel 1⁰ The moment to heel 1⁰ is a specific application of the inclining experiment formula where the transverse weight moment, (w x d), is solved for knowing the displacement, GM, and assuming an angle of inclination 1 ⁰. Transverse center of gravity, TCG, and transverse heeling moments

Example Calculate the moment to heel 1 ⁰ if your vessel’s displacement is 12,000 tons and GM is 2 feet. tan θ = (w x d)(GM)/(displacement) (w x d)=(tan 1 ⁰)(GM)(displacement) (w x d)= (0.01746)(2 feet)(12,000 tons) = 419.04 foot-tons

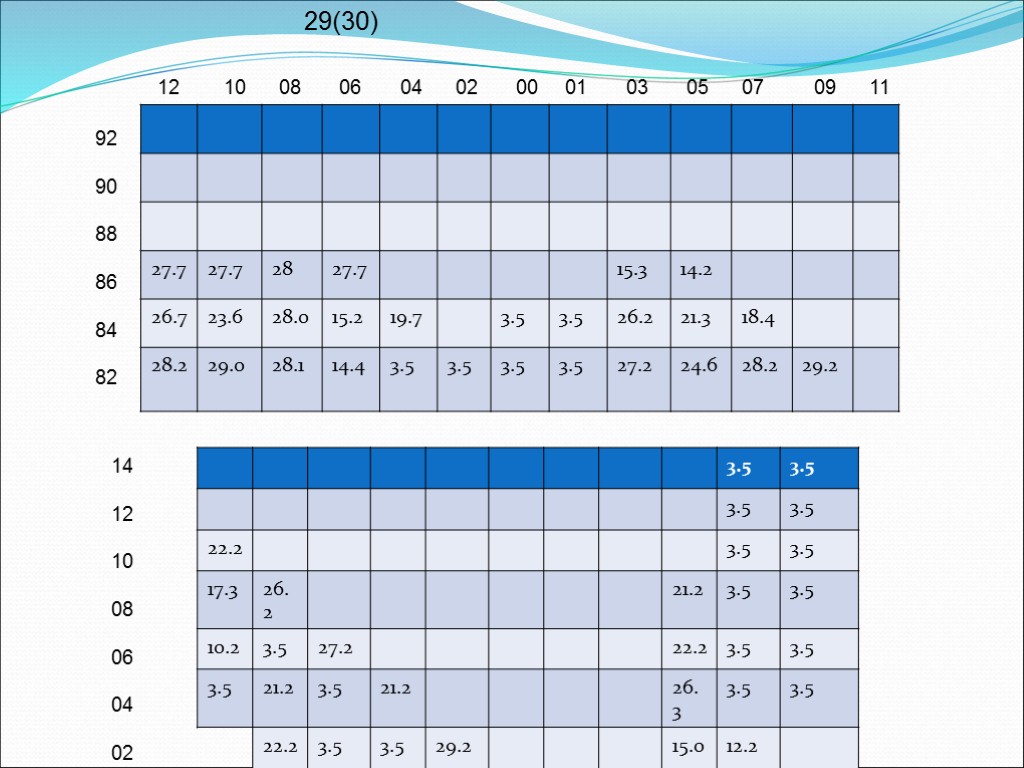
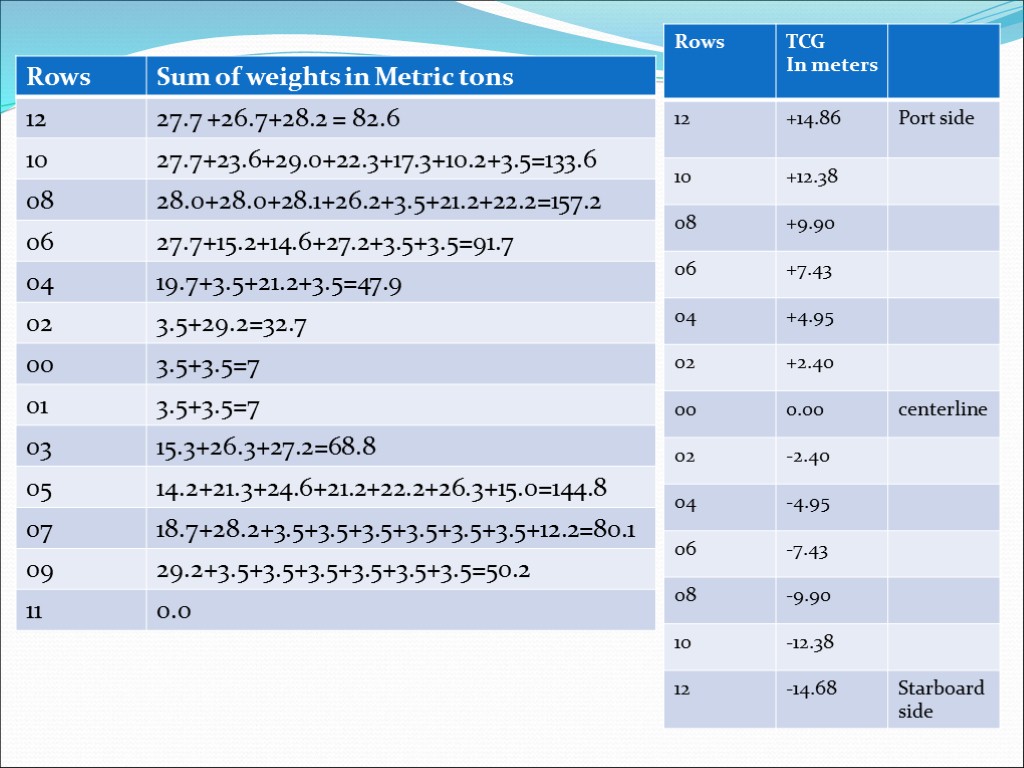
Example According to the bay plane shown in diagram, calculate the transverse heeling moment if the cargo was indicated as shown in metric tons. Assume prior to loading bay 30 the vessel is upright. If the moment to heel 1⁰ is equal to 3,500 meter-metric tons/degree, how much would this container bay list the vessel and to which direction?

12 10 08 06 04 02 00 01 03 05 07 09 11 92 90 88 86 84 82 29(30) 14 12 10 08 06 04 02

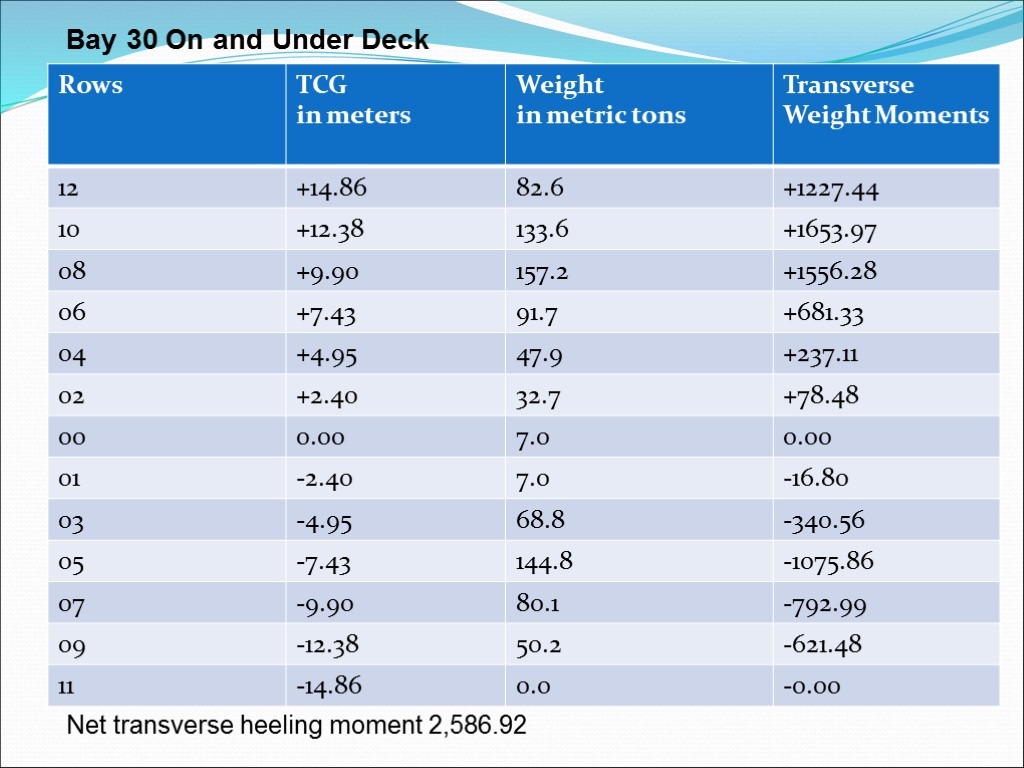
Bay 30 On and Under Deck Net transverse heeling moment 2,586.92

Estimate the angle of list Divide the net transverse heeling moment by moment to heel 1⁰ = 3,500 meter-metric tons/1⁰ Angle of list = (Net transverse heeling moment)/ (moment to heel 1⁰) = 2,586.92/3,500 = 0.74⁰ to port