What is Computer Vision Finding meaning in images

What is Computer Vision? Finding “meaning” in images How many cells are on this slide? Is there a brain tumor here? Find me some pictures of horses. Where is the road? Is there a safe path to the refrigerator? Where is the “widget” on the conveyor belt? Is there a flaw in the "widget"? 1 Where’s Waldo? Who is at the door? Ellen L. Walker

Some Applications of Computer Vision Scanning parts for defects (machine inspection) Highlighting suspect regions on CAT scans (medical imaging) Creating 3 D models of objects (or the earth!) based on multiple images Alerting a driver of dangerous situations (or steering the vehicle) Fingerprint recognition (or other biometrics) 2 Sorting envelopes with handwritten addresses (OCR) Creating performances of CGI (computer generated imagery) characters based on real actors’ movements Ellen L. Walker

Why is vision so difficult? The bar is high – consider what a toddler ‘knows’ about vision Vision is an ‘inverse problem’. Forward: one scene => one image Reverse: one image => many possible scenes ! The human visual system makes assumptions 3 Why optical illusions work (see fig. 1. 3) Ellen L. Walker

3 Approaches to Computer Vision (Szeliski) Scientific: derive algorithms from detailed models of the image formation process Vision as “reverse graphics” Statistical: use probabilistic models to describe the unknowns and noise, derive ‘most likely’ results Engineering: Find techniques that are (relatively) simple to describe and implement, but work. 4 Requires careful testing to understand limitations and costs Ellen L. Walker

Testing Vision Algorithms Pitfall: developing an algorithm that “works” on your small set of test images used during development Surprisingly common in early systems Suggested 3 -part strategy 1. 2. Add noise to your data and study degradation 3. 5 Test on clean synthetic data (e. g. graphics output) Test on real-world data, preferably from a wide range of sources (e. g. internet data, multiple ‘standard’ datasets) Ellen L. Walker

Engineering Approach to Vision Applications Start with a problem to solve Consider constraints and features of the problem Choose candidate techniques We will cover many techniques in class ! If you’re doing an IRC, I’ll try to point you in the right directions to get started 6 Implement & evaluate one or more techniques (careful testing!) Choose the combination of techniques that works best and finish implementation of system Ellen L. Walker

Scientific and Statistical Approaches Find or develop the best possible model of the physics of the system of image formation Scene geometry, light, atmospheric effects, sensors … Scientific: Invert the model mathematically to create recognition algorithms Simplify as necessary to make it mathematically tractable Take advantage of constraints / appropriate assumptions (e. g. right angles) Statistical: Determine model (distribution) parameters and/or unknowns using Bayesian techniques 7 Many machine learning techniques are relevant here Ellen L. Walker

Levels of Computer Vision Low level (image processing) Use similar algorithms for all images Nearly always required as preprocessing for HL vision Makes no assumptions about image content Techniques from signal processing, “linear systems” High level (image understanding) Often specialized for particular types of images 8 Requires models or other knowledge about image content Techniques from artificial intelligence (especially nonsymbolic AI) Ellen L. Walker

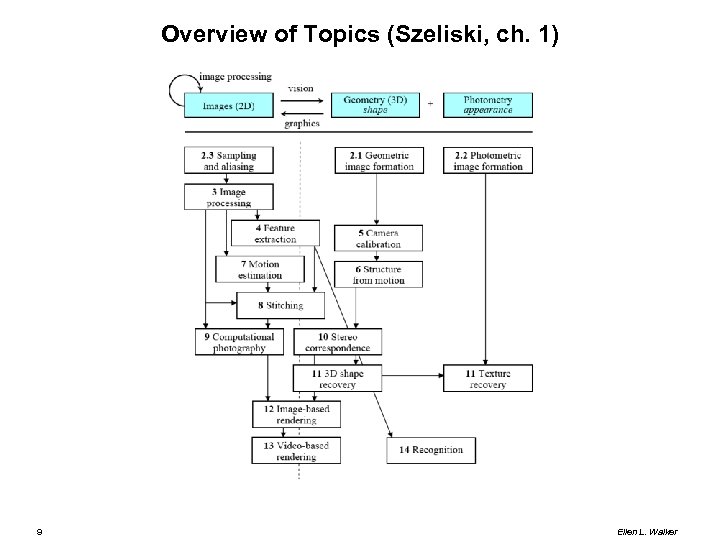Overview of Topics (Szeliski, ch. 1) 9 Ellen L. Walker

Operations on Images Low-level operators Neighborhood operations Pixel operations Whole image operations (often neighborhood in a loop) Multiple-image combination operations Image subtraction (to highlight motion) Higher-level operations 10 Compute features from an image (e. g. holes, perimeter) Compute non-iconic representations Ellen L. Walker

Object Recognition I have a model (something I want to find) Image (iconic) Geometric (2 D or 3 D) Pattern (image or features) Generic model (“idea”) I have an image (1 or more) I have questions 11 Where is M in I (if at all)? What are parameters of M that can be determined from I? Ellen L. Walker

Top-Down vs. Bottom up Top-down Example: image of “balls” - search for circles Use knowledge to guide image processing Danger: Too much top-down reasoning leads to hallucination! Bottom-up Example: edge detection -> thresholding -> feature detection 12 Extract as much from image as possible without any models Danger: “Correct” results might have nothing to do with the actual image contents Ellen L. Walker

Geometry: Point Coordinates 2 D Point x = (x, y) Actually a column vector (for matrix multiplication) Homogeneous 2 D point (includes a scale factor) x = (x, y, w) (2, 1, 1) = (4, 2, 2) = (6, 3, 3) = … Transformation: 13 (x, y) => (x, y, 1) (x, y, w) => (x/w, y/w) Special case: (x, y, 0) is “point at infinity” Ellen L. Walker

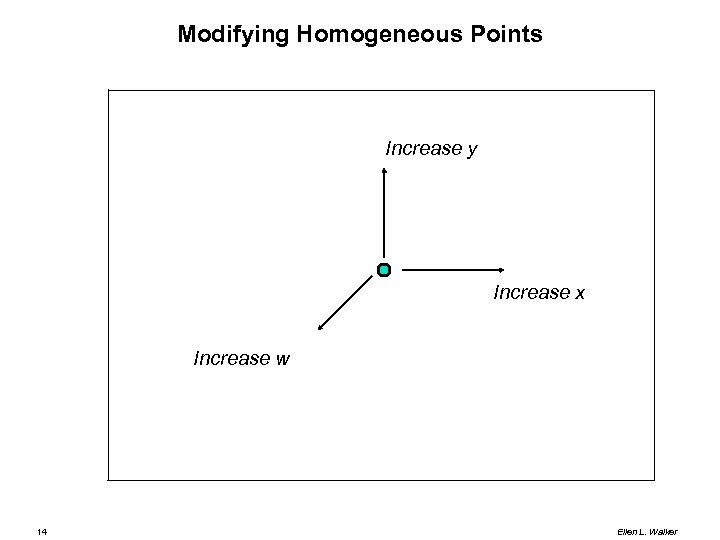Modifying Homogeneous Points Increase y Increase x Increase w 14 Ellen L. Walker

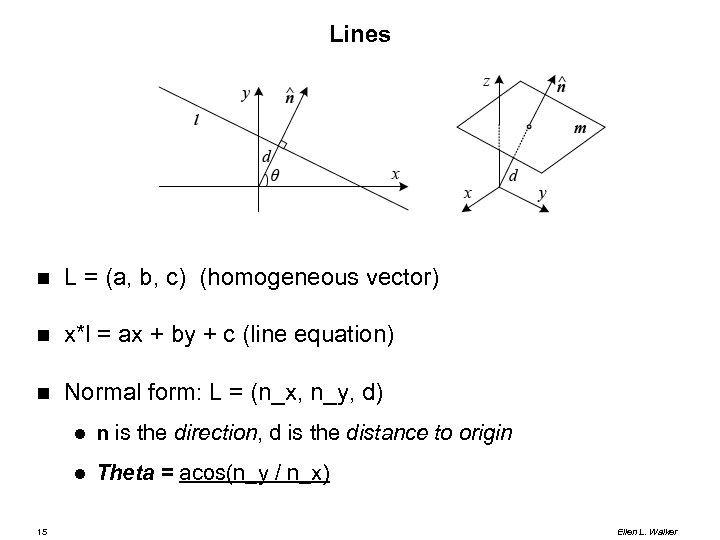Lines L = (a, b, c) (homogeneous vector) x*l = ax + by + c (line equation) Normal form: L = (n_x, n_y, d) 15 n is the direction, d is the distance to origin Theta = acos(n_y / n_x) Ellen L. Walker

Transformations 2 D to 2 D (3 x 3 matrix, multiply by homogeneous point) Coordinates r 00, r 01, r 10, r 11 specify rotation or shearing For rotation: r 00 and r 11 are cos(theta), r 01 is –sin(theta) and r 11 is sin(theta) Coordinates tx and ty are translation in x and y Coordinate s adjusts overall scale; sx and sy are 0 except for projective transform (next slide) 16 Ellen L. Walker

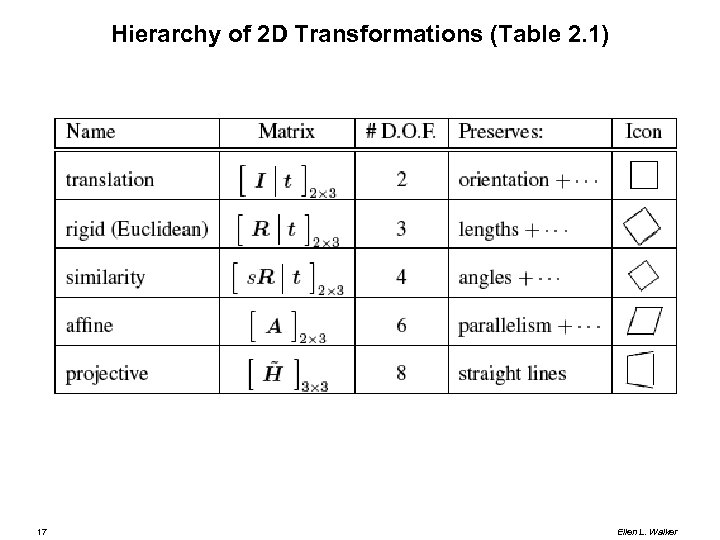Hierarchy of 2 D Transformations (Table 2. 1) 17 Ellen L. Walker

3 D Geometry Points: add another coordinate, (x, y, z, w) Planes: like lines in 2 D with an extra coordinate Lines are more complicated Possibility: represent line by 2 points on the line Any point on the line can be represented by combination of the points 18 r = (lambda)p 1 + (1 -lambda)p 2 If 0<=lambda<=1, then r is on the segment from p 1 to p 2 See 2. 1 for more details and more geometric primitives! Ellen L. Walker

3 D to 2 D Transformations These describe ways that 3 D reality can be viewed on a 2 D plane. Each is a 3 x 4 matrix Many options, see Section 2. 1. 4 19 Multiply by 3 D Homogeneous vector (4 coordinates) to get a 2 D homogeneous vector (3 coordinates) Most common is perspective projection Ellen L. Walker

Perspective Projection Geometry (Simplified) See Figure 2. 7 20 Ellen L. Walker

Simplifications of "Pinhole Model" Image plane is between the center of projection and the object rather than behind the lens as in a camera or an eye Objects are really imaged upside-down All angles, etc. are the same, though Center of projection is a virtual point (focal point of a lens) rather than a real point (pinhole) 21 Real lenses collect more light than pinholes Real lenses cause some distortion (see Figure 2. 13) Ellen L. Walker

Photometric Image Formation A surface element Reflects radiation from a single source 22 (with angle to N) Toward the sensor (with normal N) (This is called irradiance) Which senses and records it Figure 2. 14 Ellen L. Walker

Light Sources Geometry (point vs. area) Location Spectrum (white light, or only some wavelengths) Environment map (measure ambient light from all directions) Model depends on needs 23 Typical: sun = point at infinity More complex model needed for soft shadows, etc. Ellen L. Walker

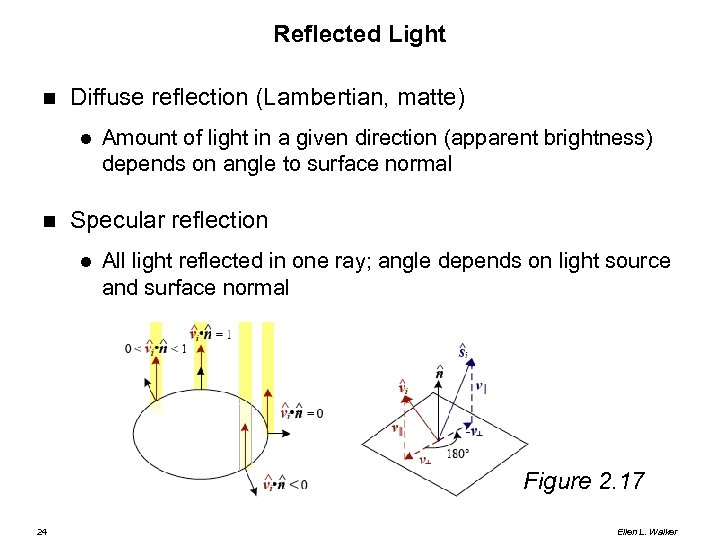Reflected Light Diffuse reflection (Lambertian, matte) Amount of light in a given direction (apparent brightness) depends on angle to surface normal Specular reflection All light reflected in one ray; angle depends on light source and surface normal Figure 2. 17 24 Ellen L. Walker

Image Sensors Charge couple device (CCD) Count photons (unit of light) that hit (one counter pixel) (Light energy converted to electrical charge) “Bleed” from neighboring pixels Each pixel reports its value (scaled by resolution) Result is a stream of numbers (0=black, MAX=white) 25 Ellen L. Walker

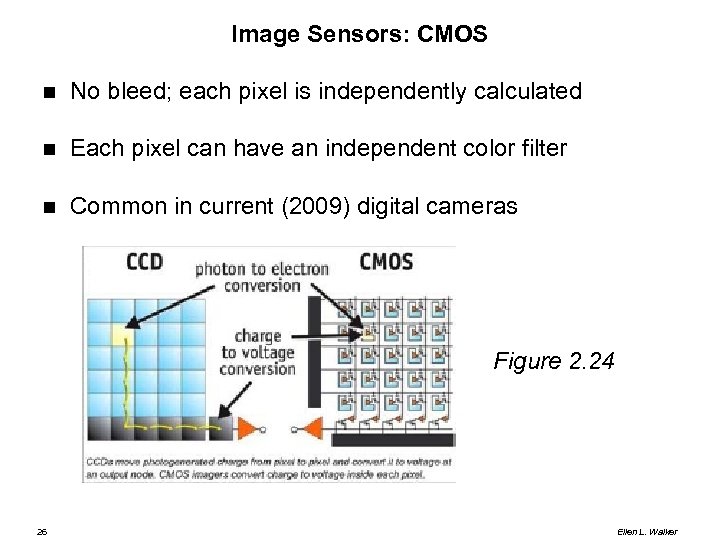Image Sensors: CMOS No bleed; each pixel is independently calculated Each pixel can have an independent color filter Common in current (2009) digital cameras Figure 2. 24 26 Ellen L. Walker

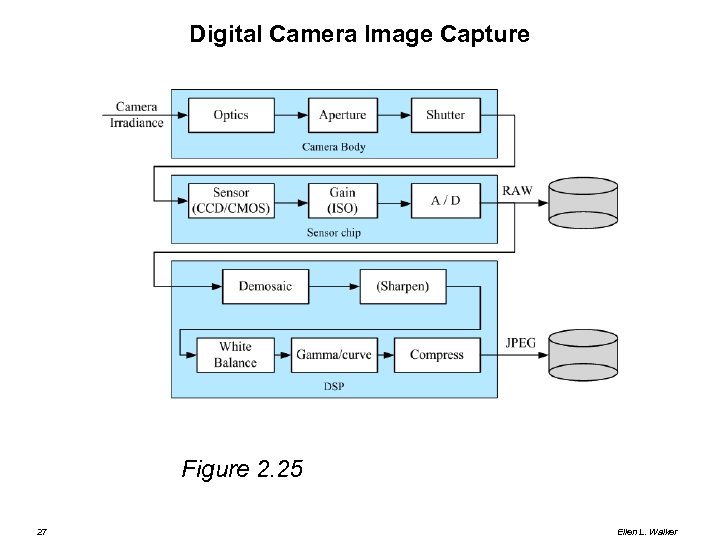Digital Camera Image Capture Figure 2. 25 27 Ellen L. Walker

Color Image Color requires 3 values to specify (3 images) Cyan, Magenta, Yellow, Black (CMYK): printing YIQ (Y is intensity, I is “lightness”): color TV signal (Y is B/W signal) Red, green, blue (RGB) : computer monitor Hue, Saturation, Intensity: Hue = pure color, saturation = density of color, intensity = b/w signal (“color-picker”) Visible color depends on color of object, color of light, material of object, and colors of nearby objects! (There is a whole subfield of vision that “explains” color in images. See section 2. 3. 2 for more details and pointers) 28 Ellen L. Walker

Problems with Images Geometric Distortion (e. g. barrel distortion) - from lenses Scattering - e. g. thermal "lens" in atmosphere - fog is an extreme case Blooming - CCD cells affect each other Sensor cell variations - "dead cell" is an extreme case Discretization effects (clipping or wrap around) - (256 becomes 0) Chromatic distortion (color "spreading" effect) Quantization effects (fitting a circle into squares, e. g. ) 29 Ellen L. Walker

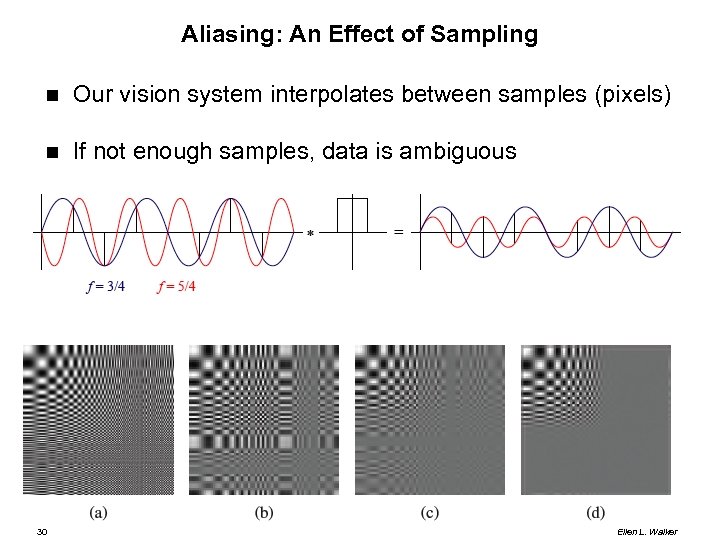Aliasing: An Effect of Sampling Our vision system interpolates between samples (pixels) If not enough samples, data is ambiguous 30 Ellen L. Walker

Image Types Analog image - the ideal image, with infinite precision spatial (x, y) and intensity f(x, y) is called the picture function Digital image - sampled analog image; a discrete array I[r, c] with limited precision (rows, columns, max I) If all pixel values are 0 or 1, I[r, c] is a binary image M[r, c] is a multispectral image. Each pixel is a vector of values, e. g. (R, G, B) 31 I[r, c] is a gray-scale image L[r, c] is a labeled image. Each pixel is a symbol denoting the outcome of a decision, e. g. grass vs. sky vs. house Ellen L. Walker

Coordinate systems Raster coordinate system Origin (0, 0) is at upper left Derives from printing an array on a line printer Row (R) increases downward; Column (C) increase to right Cartesian coordinate system Origin (0, 0) is at lower left Typical system used in mathematics X increases to the right; Y increases upward Conversions 32 Y = Max. Rows - R ; X = C Or, pretend X=R, Y=C then rotate your printout 90 degrees! Ellen L. Walker

Resolution In general, resolution is related to a sensor's measurement precision or ability to detect fine features Nominal resolution of a sensor is the size of the scene element that images to a singel pixel on the image plane Resolution of a camera (or an image) is also the number of rows & columns it contains (or their product), e. g. "8 megapixel resolution" Subpixel Resolution means that the precision of measurement is less than the nominal resolution (e. g. subpixel resolution of positions on a line segment) 33 Ellen L. Walker

Variation in Resolution 34 Ellen L. Walker

Quantization Errors One pixel contains a mixture of materials 10 m x 10 m area in a satellite photo Across the edge of a painted stripe or character Subpixel shift in location has major effect on image! Shape distortions caused by quantization ("jaggies") Change / loss in features 35 Thin stripe lost Area varies based on resolution (e. g. circle) Ellen L. Walker

Representing an Image file header Type (binary, grayscale, color, video sequence) Creation date Title Dimensions (#rows, #cols, #bits / pixel) History (nice) Data 36 Values for all pixels, in a pre-defined order based on the format Might be compressed (e. g. JPEG is lossy compression) Ellen L. Walker

PNM: a simple image representation Portable N Map Pgm = portable gray map Pbm = portable bit map Ppm = portable pixel map (color image) Image. J reads, displays, and converts PNM images. (pbm, pgm, ppm) – and much more! 37 GIF, JPG and other formats can be converted (both ways) Image. J does not appear to convert color to grayscale Irfanview (Windows only) reads, displays and converts Ellen L. Walker

PNM Details Comments can be anywhere after Px - lines begin with # First Px (where x is an integer from 1 -6) P 1/4 = binary, P 2/5 = gray, P 3/6 = color P 1 -P 3: data in ascii, P 4 -P 6: data in binary Next come 2 integers (#cols, #rows) Next (unless it’s P 1 or P 4) comes 1 integer (#greylevels) The rest of the image is pixel values from 0 to #greylevels – 1 (If color: red image, then green, then blue) 38 Ellen L. Walker

PGM image example This one is really boring! P 2 32 4 000123 39 Ellen L. Walker

Other Image Formats GIF (Compuserve - commercial) 8 -bit color (uses a colormap) LZW lossless compression available TIFF (Aldus Corp. , for scanners) Multiple images, 1 -24 bits / pixel color Lossy or lossless compression available JPEG (Joint Photographic Experts Group - free) Real-time encoding/decoding in hardware 40 Lossy compression Up to 64 K x 24 bits Ellen L. Walker

Specifying a vision system Inputs Environment (e. g. light(s), fixtures for holding objects, etc. ) OR unconstrained environments Sensor(s) OR someone else's images Resolution & formats of image(s) Algorithms To be studied in detail later(!) Results 41 Image(s) Non-iconic results Ellen L. Walker

If you're doing an IRC… (Example from 2002) What is the goal of your project? How will you get data (see "Inputs" last slide) Camera above monitor; user at (relatively) fixed distance Determine what kind of results you need Eye-tracking to control a cursor - hands-free game operation Outputs to control cursor How will you judge success? 42 User is satisfied that cursor does what he/she wants Works for many users, under range of conditions Ellen L. Walker

Staging your project What can be done in 3 weeks? 6 weeks? 9 weeks? 1. 2. Reliably track eye direction between a single pair of images (output "left", "right", "up", "down") [DONE] 3. Find the eyes in a single image [DONE] Use a continuous input stream (preferably real time) [NOT DONE] Program defensively Keep printouts as last-ditch backups When a milestone is reached, make a copy of the code and freeze it! (These can be smaller than the 3 -week ideas above) 43 Back up early and often! (and in many places) When time runs out, submit and present your best frozen milestone. Ellen L. Walker