What is a NP problem n n Given

What is a NP problem? n n Given an instance of the problem, V, and a ‘certificate’, C, we can verify V is in the language in polynomial time All problems in P are NP problems n Why?

What is NP-Complete? n A problem is NP-Complete if: It is in NP n Every other NP problem has a polynomial time reduction to this problem n n NP-Complete problems: 3 -SAT n VERTEX-COVER n CLIQUE n HAMILTONIAN-PATH (HAMPATH) n

Dilemma n n n NP problems need solutions in real-life We only know exponential algorithms What do we do?

A Solution n There are many important NP-Complete problems n n There is no fast solution ! But we want the answer … If the input is small use backtrack. n Isolate the problem into P-problems ! n Find the Near-Optimal solution in polynomial time. n 5

Accuracy n n n NP problems are often optimization problems It’s hard to find the EXACT answer Maybe we just want to know our answer is close to the exact answer?

Approximation Algorithms n n Can be created for optimization problems The exact answer for an instance is OPT The approximate answer will never be far from OPT We CANNOT approximate decision problems

Performance ratios n n We are going to find a Near-Optimal solution for a given problem. We assume two hypothesis : Each potential solution has a positive cost. n The problem may be either a maximization or a minimization problem on the cost. n 8

Performance ratios … n n If for any input of size n, the cost C of the solution produced by the algorithm is within a factor of ρ(n) of the cost C* of an optimal solution: Max ( C/C* , C*/C ) ≤ ρ(n) We call this algorithm as an ρ(n)approximation algorithm. 9

Performance ratios … n n In Maximization problems: C*/ρ(n) ≤ C* In Minimization Problems: C* ≤ C ≤ ρ(n)C* n n n ρ(n) is never less than 1. A 1 -approximation algorithm is the optimal solution. The goal is to find a polynomial-time approximation algorithm with small constant approximation ratios.

Approximation scheme n n Approximation scheme is an approximation algorithm that takes Є>0 as an input such that for any fixed Є>0 the scheme is (1+Є)-approximation algorithm. Polynomial-time approximation scheme is such algorithm that runs in time polynomial in the size of input. n As the Є decreases the running time of the algorithm can increase rapidly: n For example it might be O(n 2/Є) 11

Approximation scheme n We have Fully Polynomial-time approximation scheme when its running time is polynomial not only in n but also in 1/Є n For example it could be O((1/Є)3 n 2) 12

Some examples: n n n Vertex cover problem. Traveling salesman problem. Set cover problem. 13

VERTEX-COVER n Given a graph, G, return the smallest set of vertices such that all edges have an end point in the set

The vertex-cover problem n n n A vertex-cover of an undirected graph G is a subset of its vertices such that it includes at least one end of each edge. The problem is to find minimum size of vertex-cover of the given graph. This problem is an NP-Complete problem. 15

The vertex-cover problem … n n Finding the optimal solution is hard (it’s NP!) but finding a near-optimal solution is easy. There is an 2 -approximation algorithm: n It returns a vertex-cover not more than twice of the size optimal solution. 16

The vertex-cover problem … APPROX-VERTEX-COVER(G) 1 C←Ø 2 E′ ← E[G] 3 while E′ ≠ Ø 4 do let (u, v) be an arbitrary edge of E′ 5 C ← C U {u, v} 6 remove every edge in E′ incident on u or v 7 return C 17

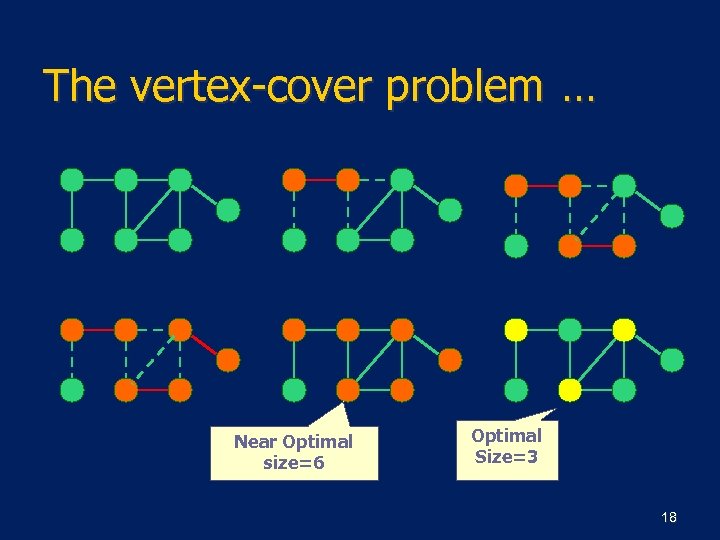
The vertex-cover problem … Near Optimal size=6 Optimal Size=3 18

The vertex-cover problem … n This is a polynomial-time 2 -aproximation algorithm. (Why? ) n Because: n n Optimal APPROX-VERTEX-COVER is O(V+E) |C*| ≥ |A| Selected Edges |C| = 2|A| |C| ≤ 2|C*| Selected Vertices 19

Minimum Spanning Tree n n Given a graph, G, a Spanning Tree of G is a subgraph with no cycles that connects every vertex together A MST is a Spanning Tree with minimal weight

Finding a MST n n Finding a MST can be done in polynomial time using PRIM’S ALGORITHM or KRUSKAL’S ALGORITHM Both are greedy algorithms

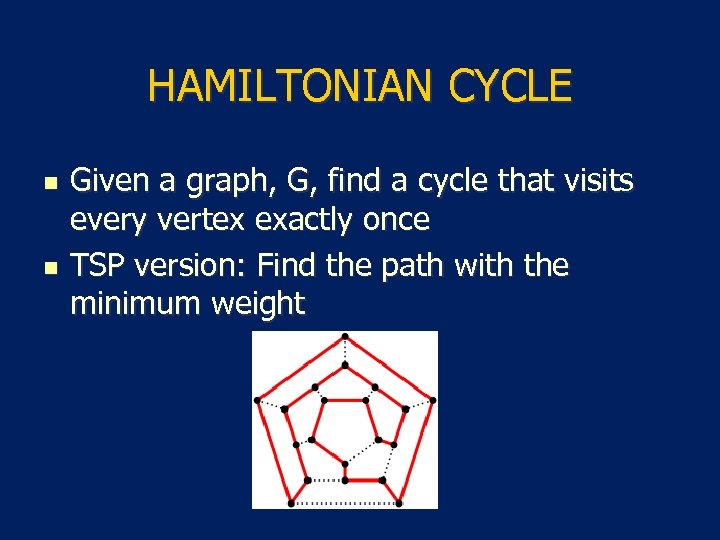
HAMILTONIAN CYCLE n n Given a graph, G, find a cycle that visits every vertex exactly once TSP version: Find the path with the minimum weight

MST vs HAM-CYCLE n n Any HAM-CYCLE becomes a Spanning Tree by removing an edge cost(MST) ≤ cost(min-HAM-CYCLE)

Traveling salesman problem n n n Given an undirected complete weighted graph G we are to find a minimum cost Hamiltonian cycle. Satisfying triangle inequality or not this problem is NP-Complete. The problem is called Euclidean TSP. 24

Traveling salesman problem n Near Optimal solution Faster n Easier to implement. n 25

Euclidian Traveling Salesman Problem APPROX-TSP-TOUR(G, W) 1 2 3 4 select a vertex r Є V[G] to be root. compute a MST for G from root r using Prim Alg. L=list of vertices in preorder walk of that MST. return the Hamiltonian cycle H in the order L. 26

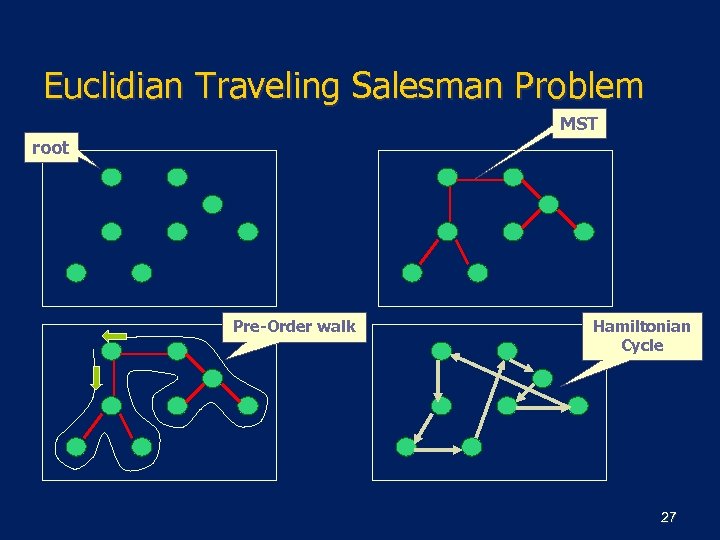
Euclidian Traveling Salesman Problem MST root Pre-Order walk Hamiltonian Cycle 27

Traveling salesman problem n This is polynomial-time 2 -approximation algorithm. (Why? ) n Because: n n Pre-order Solution APPROX-TSP-TOUR is O(V 2) C(MST) ≤ C(H*) C(W)=2 C(MST) C(W)≤ 2 C(H*) C(H)≤C(W) C(H)≤ 2 C(H*) Optimal H*: optimal soln W: Preorder walk H: approx soln & triangle inequality 28

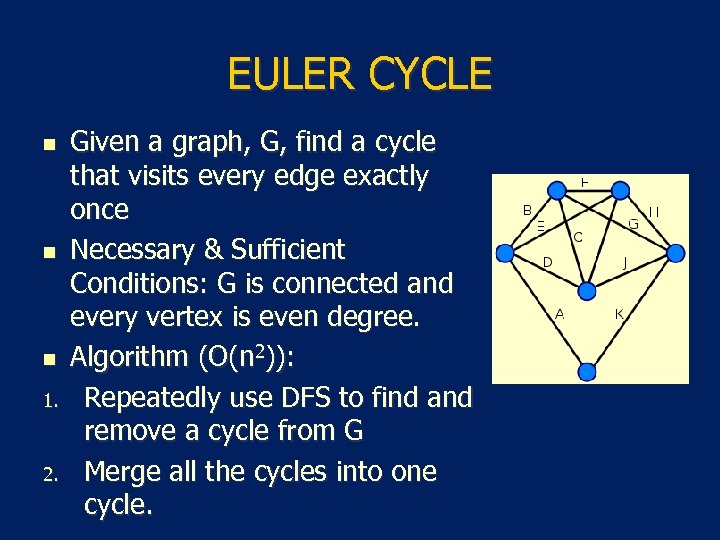
EULER CYCLE n n n 1. 2. Given a graph, G, find a cycle that visits every edge exactly once Necessary & Sufficient Conditions: G is connected and every vertex is even degree. Algorithm (O(n 2)): Repeatedly use DFS to find and remove a cycle from G Merge all the cycles into one cycle.

Min-Weight Matching n n Given a complete weighted graph of even nodes, G, find a perfect matching of minimum total weight Algorithm (O(n 3)): Formulated as a linear programming problem, but solved using a special algorithm.

Euclidian Traveling Salesman Problem APPROX-TSP-TOUR 2(G, c) 1 Select a vertex r Є V[G] to be root. 2 Compute a MST T for G from root r using Prim Alg. 3 Find a minimal-weight matching M for vertices of odd degree in T. 4 Find an Euler cycle C in G’ = (V, T U M). 5 L=list of vertices in preorder walk of C. 6 return the Hamiltonian cycle H in the order L. 31

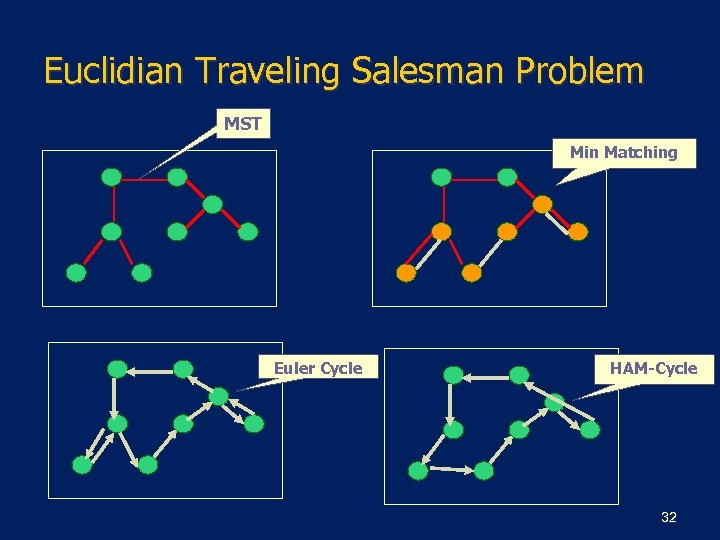
Euclidian Traveling Salesman Problem MST Min Matching Euler Cycle HAM-Cycle 32

Time Complexity APPROX-TSP-TOUR 2(G, c) 1 2 3 4 5 6 Select a vertex r Є V[G] to be root. Compute a MST T for G from root r using Prim Alg. Find a minimal-weight matching M for vertices of odd degree in T. Find an Euler cycle A in G’ = (V, T U M). L=list of vertices in preorder walk of A. return the Hamiltonian cycle H in order L. O(1) O(n lg n) O(n 3) O(n 2) O(n) 33

Traveling salesman problem n This is polynomial-time 3/2 -approximation algorithm. (Why? ) n Because: n n Min match Euler cycle Solution APPROX-TSP-TOUR 2 is O(n 3) C(MST) ≤ C(H*) Optimal C(M) ≤ 0. 5 C(H*) C(A) = C(MST)+C(M) C(H) ≤ C(A) C(H) ≤ 1. 5 C(H*) H*: optimal soln M: min matching A: Euler cycle H: approx soln & triangle inequality 34

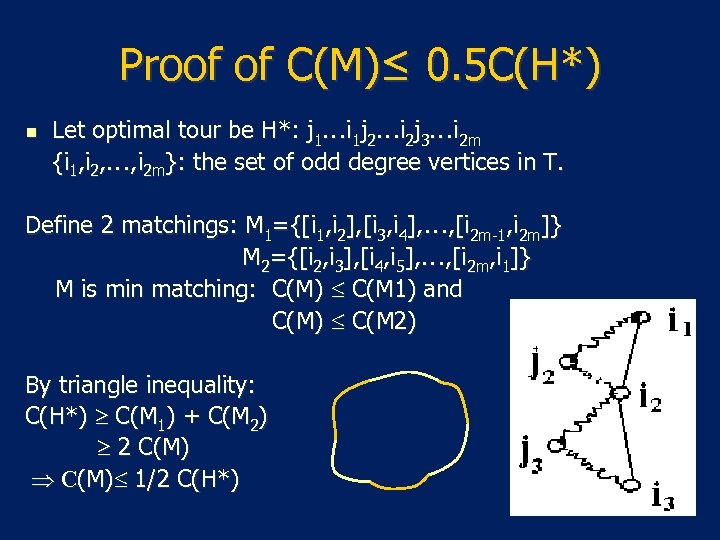
Proof of C(M)≤ 0. 5 C(H*) n Let optimal tour be H*: j 1…i 1 j 2…i 2 j 3…i 2 m {i 1, i 2, …, i 2 m}: the set of odd degree vertices in T. Define 2 matchings: M 1={[i 1, i 2], [i 3, i 4], …, [i 2 m-1, i 2 m]} M 2={[i 2, i 3], [i 4, i 5], …, [i 2 m, i 1]} M is min matching: C(M) C(M 1) and C(M) C(M 2) By triangle inequality: C(H*) C(M 1) + C(M 2) 2 C(M) 1/2 C(H*)

TSP In General n n Theorem: If P ≠ NP, then for any constant ρ>1, there is no polynomial time ρ-approximation algorithm. Proof: If we have a polynomial time ρ-approximation algorithm for TSP, we can find a tour of cost ρH*. n c(u, w) = if ((u, w) in E) then 1 else ρ|V|+1 n The optimal cost H* of a TSP tour is |V|. n G has a Ham-cycle iff TSP has a tour of cost ρ|V|. n If a TSP tour has one edge of cost ρ|V|+1, then the total cost is (ρ|V|+1)+|V|-1>ρ|V| Selected edge not in E Rest of edges 36

The Set-Cover Problem n Instance (X, F) : X : a finite set of elements. n F : family of subsets of X. n Solution C : subset of F that includes all the members of X. n n n Set-Cover is in NP Set-Cover is NP-hard, as it’s a generalization of vertex-cover problem. 37

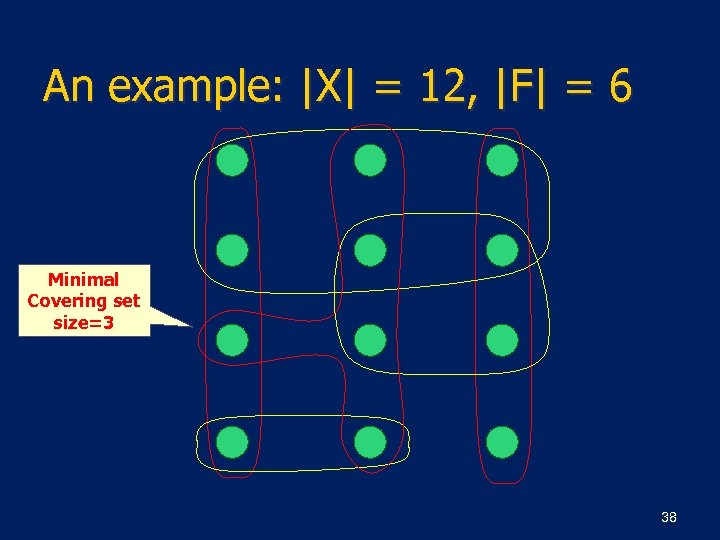
An example: |X| = 12, |F| = 6 Minimal Covering set size=3 38

A Greedy Algorithm GREEDY-SET-COVER(X, F) 1 M←X 2 C←Ø 3 while M ≠ Ø do 4 select S Є F that maximizes |S ח M| 5 M←M–S 6 C ← C U {S} 7 return C 39

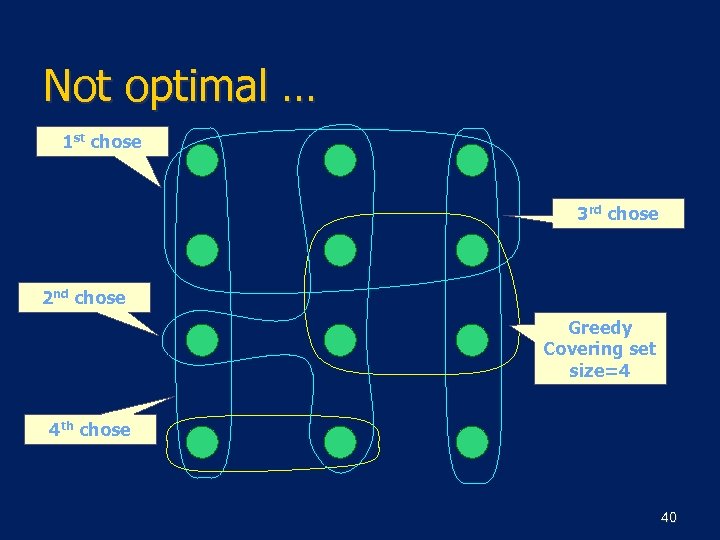
Not optimal … 1 st chose 3 rd chose 2 nd chose Greedy Covering set size=4 4 th chose 40

Set-Cover … n This greedy algorithm is polynomialtime ρ(n)-approximation algorithm n ρ(n)=lg(n) 41

The bin packing problem n n n items a 1, a 2, …, an, 0 ai 1, 1 i n, to determine the minimum number of bins of unit capacity to accommodate all n items. E. g. n = 5, {0. 3, 0. 5, 0. 8, 0. 2 0. 4} n The bin packing problem is NP-hard.

APPROXIMATE BIN PACKING n Problem: fill in objects each of size<= 1, in minimum number of bins (optimal) each of size=1 (NP-complete). Online problem: do not have access to the full set: incremental; Offline problem: can order the set before starting. n Theorem: No online algorithm can do better than n n 4/3 of the optimal #bins, for any given input set.

NEXT-FIT ONLINE BIN-PACKING n n n If the current item fits in the current bin put it there, otherwise move on to the next bin. Linear time with respect to #items - O(n), for n items. Theorem: Suppose, M optimum number of bins are needed for an input. Next-fit never needs more than 2 M bins. Proof: Content(Bj) + Content(Bj+1) >1, So, Wastage(Bj) + Wastage(Bj+1)<2 -1, Average wastage<0. 5, less than half space is wasted, so, should not need more than 2 M bins.

FIRST-FIT ONLINE BIN-PACKING n n Scan the existing bins, starting from the first bin, to find the place for the next item, if none exists create a new bin. O(N 2) naïve, O(N log. N) possible, for N items. Obviously cannot need more than 2 M bins! Wastes less than Next-fit. Theorem: Never needs more than Ceiling(1. 7 M). Proof: too complicated. For random (Gaussian) input sequence, it takes 2% more than optimal, observed empirically. Great!

BEST-FIT ONLINE BIN-PACKING n n Scan to find the tightest spot for each item (reduce wastage even further than the previous algorithms), if none exists create a new bin. Does not improve over First-Fit in worst case in optimality, but does not take more worst-case time either! Easy to code.

OFFLINE BIN-PACKING n n Create a non-increasing order (larger to smaller) of items first and then apply some of the same algorithms as before. Theorem: If M is optimum #bins, then First-fit-offline will not take more than M + (1/3)M #bins.

Polynomial-Time Approximation Schemes n n A problem L has a fully polynomial-time approximation scheme (FPTAS) if it has a polynomial-time (in n and 1/ε) (1+ε)-approximation algorithm, for any fixed ε >0. 0/1 Knapsack has a FPTAS, with a running time that is O(n 3 / ε).

Knapsack Problem Knapsack problem. Given n objects and a "knapsack. " we'll assume w i W Item i has value vi > 0 and weighs wi > 0. Knapsack can carry weight up to W. Goal: fill knapsack so as to maximize total value. n n Item W = 11 Value Weight 1 Ex: { 3, 4 } has value 40. 1 1 2 6 2 3 18 5 4 22 6 5 28 7 49

Knapsack is NP-Complete KNAPSACK: Given a finite set X, nonnegative weights wi, nonnegative values vi, a weight limit W, and a target value V, is there a subset S X such that: SUBSET-SUM: Given a finite set X, nonnegative values ui, and an integer U, is there a subset S X whose elements sum to exactly U? Claim. SUBSET-SUM P KNAPSACK. Pf. Given instance (u 1, …, un, U) of SUBSET-SUM, create KNAPSACK instance: 50

Knapsack Problem: Dynamic Programming 1 Def. OPT(i, w) = max value subset of items 1, . . . , i with weight limit w. Case 1: OPT does not select item i. – OPT selects best of 1, …, i– 1 using up to weight limit w Case 2: OPT selects item i. – new weight limit = w – wi – OPT selects best of 1, …, i– 1 using up to weight limit w – w i n n Running time. O(n W). W = weight limit. Not polynomial in input size! n n 51

Knapsack Problem: Dynamic Programming II Def. OPT(i, v) = min weight subset of items 1, …, i that yields value exactly v. Case 1: OPT does not select item i. – OPT selects best of 1, …, i-1 that achieves exactly value v Case 2: OPT selects item i. – consumes weight wi, new value needed = v – vi – OPT selects best of 1, …, i-1 that achieves exactly value v n n 52

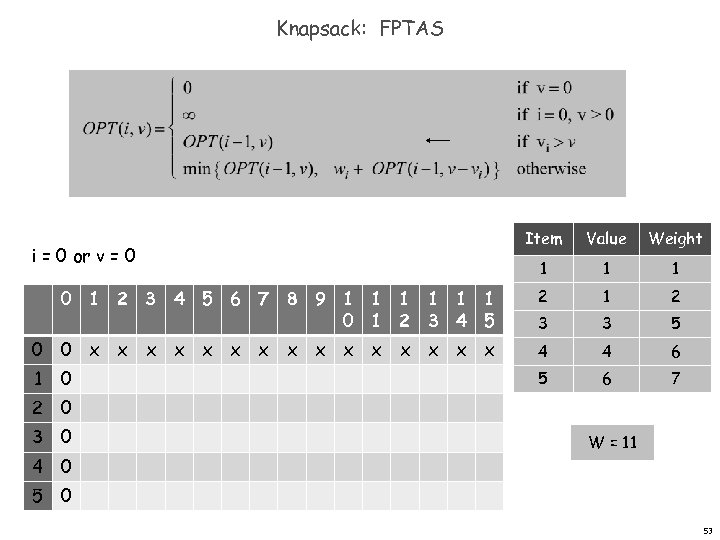
Knapsack: FPTAS Item Value Weight 1 1 1 0 1 2 3 4 5 6 7 8 9 1 1 1 0 1 2 3 4 5 2 1 2 3 3 5 0 0 x x x x 4 4 6 1 5 6 7 i = 0 or v = 0 0 2 0 3 0 W = 11 4 0 53

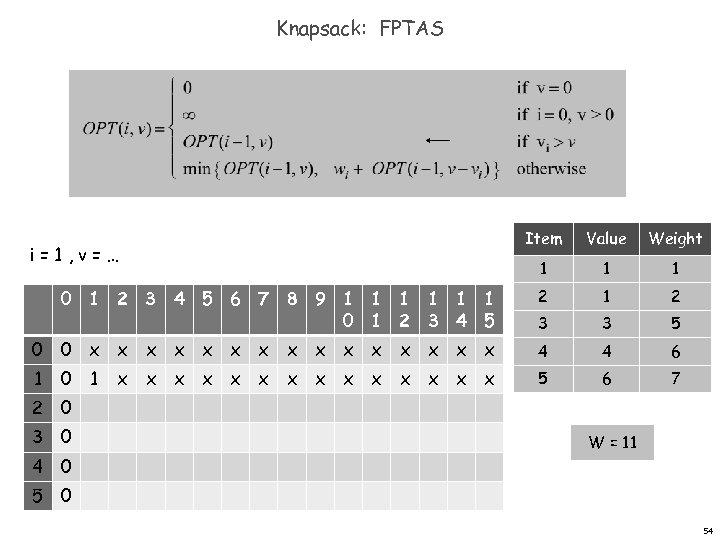
Knapsack: FPTAS Item Value Weight 1 1 1 0 1 2 3 4 5 6 7 8 9 1 1 1 0 1 2 3 4 5 2 1 2 3 3 5 0 0 x x x x 4 4 6 1 5 6 7 i=1, v=… 0 1 x x x x 2 0 3 0 W = 11 4 0 54

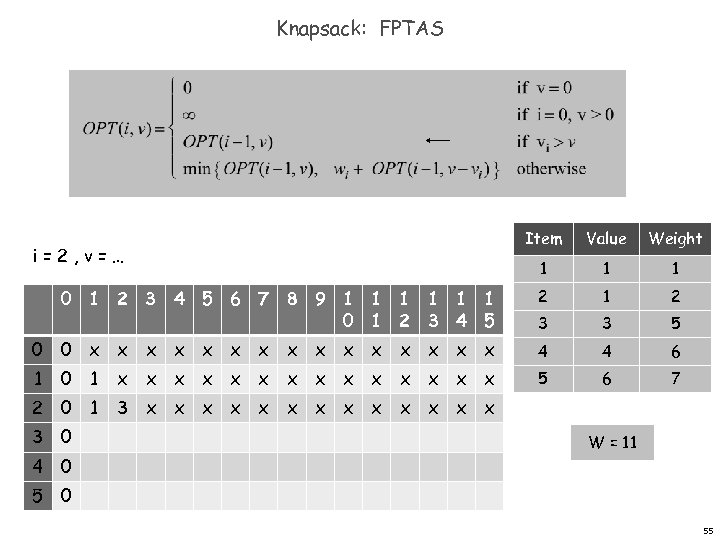
Knapsack: FPTAS Item Value Weight 1 1 1 0 1 2 3 4 5 6 7 8 9 1 1 1 0 1 2 3 4 5 2 1 2 3 3 5 0 0 x x x x 4 4 6 1 5 6 7 i=2, v=… 0 1 x x x x 2 0 1 3 x x x x 3 0 W = 11 4 0 55

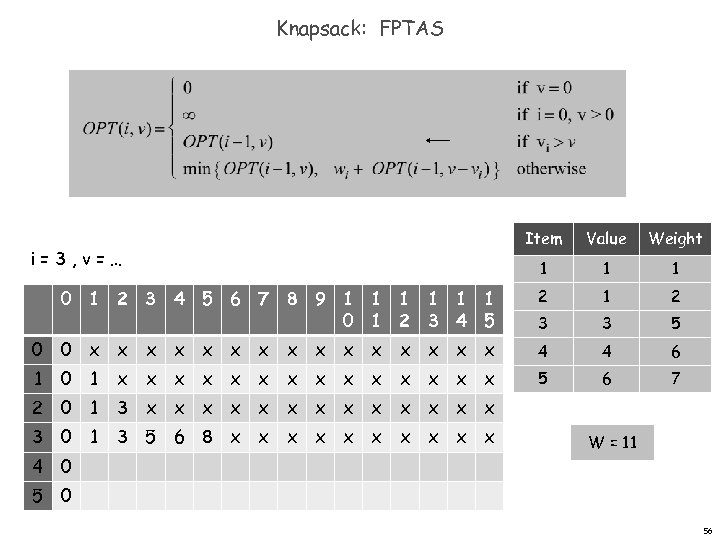
Knapsack: FPTAS Item Value Weight 1 1 1 0 1 2 3 4 5 6 7 8 9 1 1 1 0 1 2 3 4 5 2 1 2 3 3 5 0 0 x x x x 4 4 6 1 5 6 7 i=3, v=… 0 1 x x x x 2 0 1 3 x x x x 3 0 1 3 5 6 8 x x x x x W = 11 4 0 56

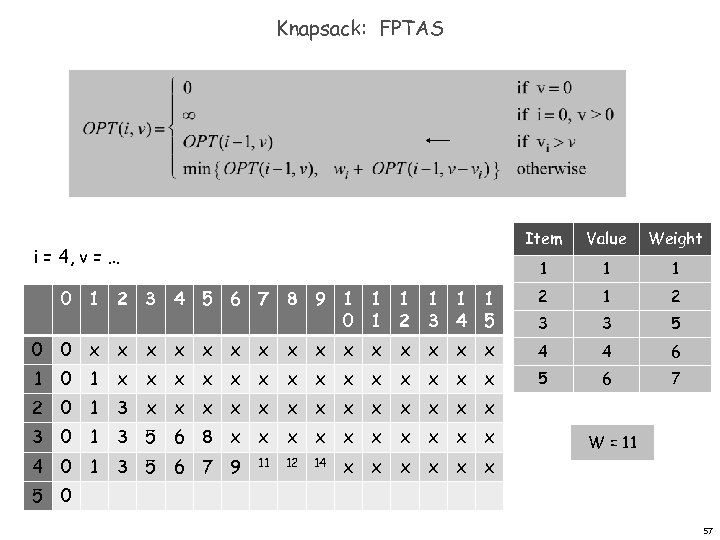
Knapsack: FPTAS Item Value Weight 1 1 1 0 1 2 3 4 5 6 7 8 9 1 1 1 0 1 2 3 4 5 2 1 2 3 3 5 0 0 x x x x 4 4 6 1 5 6 7 i = 4, v = … 0 1 x x x x 2 0 1 3 x x x x 3 0 1 3 5 6 8 x x x x x 4 0 1 3 5 6 7 9 11 12 14 W = 11 x x x 5 0 57

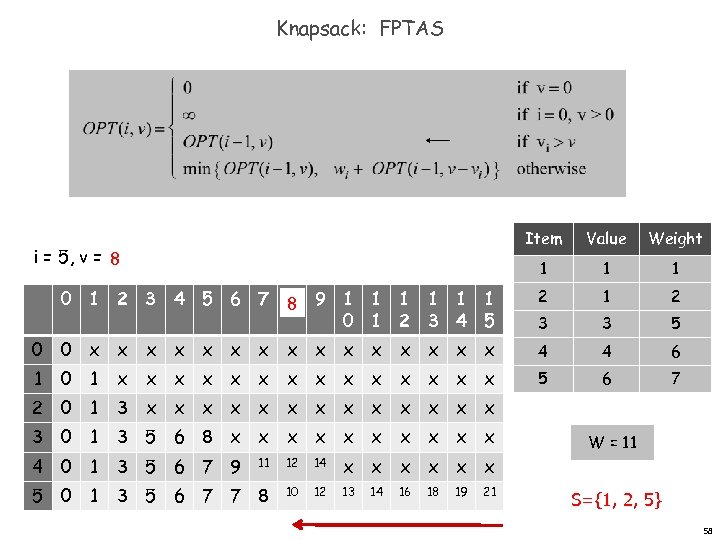
Knapsack: FPTAS Item Value Weight 1 1 1 0 1 2 3 4 5 6 7 8 9 1 1 1 8 0 1 2 3 4 5 2 1 2 3 3 5 0 0 x x x x 4 4 6 1 5 6 7 i = 5, v = … 8 0 1 x x x x 2 0 1 3 x x x x 3 0 1 3 5 6 8 x x x x x 4 0 1 3 5 6 7 9 11 12 14 x x x 5 0 1 3 5 6 7 7 8 10 12 13 14 16 18 19 21 W = 11 S={1, 2, 5} 58

Knapsack: FPTAS Tracing Solution // first call: pick_item(n, v) where M[n, v] <= W and v is max pick_item( i, v) { if (v == 0) return; if (M[i, v] == wi + M[i-1, v-vi]) { print i; pick_item(i-1, v-vi); print i; } else pick_item(i-1, v); } Item Value Weight 1 1 1 0 1 2 3 4 5 6 7 8 9 1 1 1 8 0 1 2 3 4 5 2 1 2 3 3 5 0 0 x x x x 4 4 6 1 5 6 7 i = 5, v = … 8 0 1 x x x x 2 0 1 3 x x x x 3 0 1 3 5 6 8 x x x x x 4 0 1 3 5 6 7 9 11 12 14 x x x 5 0 1 3 5 6 7 7 8 10 12 13 14 16 18 19 21 W = 11 S={1, 2, 5} 59

Knapsack Problem: Dynamic Programming II Def. OPT(i, v) = min weight subset of items 1, …, i that yields value exactly v. Case 1: OPT does not select item i. – OPT selects best of 1, …, i-1 that achieves exactly value v Case 2: OPT selects item i. – consumes weight wi, new value needed = v – vi – OPT selects best of 1, …, i-1 that achieves exactly value v n n V* n vmax Running time. O(n V*) = O(n 2 vmax). V* = optimal value = maximum v such that OPT(n, v) W. Not polynomial in input size! n n 60

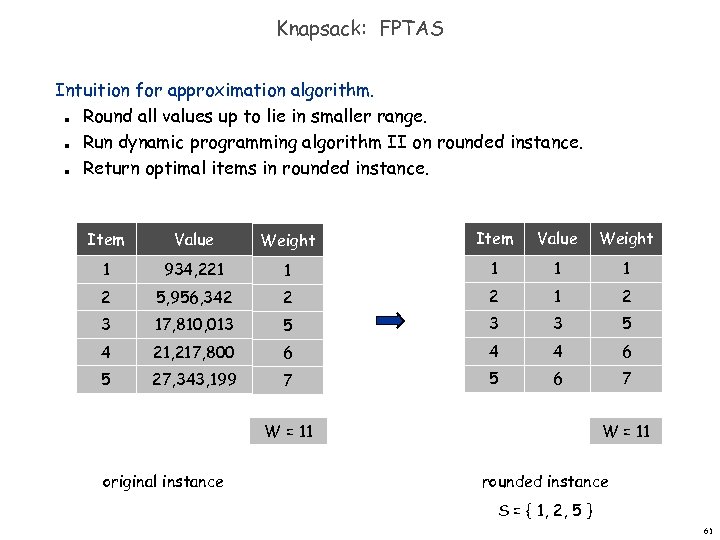
Knapsack: FPTAS Intuition for approximation algorithm. Round all values up to lie in smaller range. Run dynamic programming algorithm II on rounded instance. Return optimal items in rounded instance. n n n Item Value Weight 1 934, 221 1 1 2 5, 956, 342 2 2 1 2 3 17, 810, 013 5 3 3 5 4 21, 217, 800 6 4 4 6 5 27, 343, 199 7 5 6 7 W = 11 original instance W = 11 rounded instance S = { 1, 2, 5 } 61

Knapsack: FPTAS Knapsack FPTAS. Round up all values: vmax = largest value in original instance – = precision parameter – = scaling factor = vmax / n – Observation. Optimal solution to problems with or are equivalent. Intuition. close to v so optimal solution using is nearly optimal; small and integral so dynamic programming algorithm is fast. Running time. O(n 3 / ). Dynamic program II running time is n , where 62

Knapsack: FPTAS Knapsack FPTAS. Round up all values: Theorem. If S is solution found by our algorithm and S* is any other feasible solution of the original problem, then Pf. Let S* be any feasible solution satisfying weight constraint. always round up solve rounded instance optimally never round up by more than |S| n DP alg can take vmax n = vmax, vmax i S vi 63