daeb31bd118d8ce8731602103f0e5653.ppt
- Количество слайдов: 26

What does genetic programming teach us about the foreign exchange market ? Chris Neely* Paul Weller † Rob Dittmar** December 1 -2, 1998 * Economist, Federal Reserve Bank of St. Louis † Professor, Department of Finance, University of Iowa ** Scientific Programmer, Federal Reserve Bank of St. Louis 1

Disclaimer The views expressed are my own and do not necessarily reflect official positions of the Federal Reserve Bank of St. Louis, or the Federal Reserve System. 2

What does genetic programming teach us about foreign exchange markets? I) Broad overview of an ongoing project II) Foreign exchange market efficiency and technical analysis III) What is genetic programming? IV) Results from dollar exchange rates V) Results from the European Monetary System VI) Results using Federal Reserve Intervention VII) Work in Progress 3

II) Foreign exchange market efficiency and technical analysis A) Foreign exchange market efficiency 1) Exchange rates reflect information to the point where the potential excess returns do not exceed the transactions costs of acting (trading) on that information (Jensen, 1978). 2) Borrowing in one currency to lend in another should not profit you, except to the extent that this is risky strategy. 4

5

B) The puzzle of technical analysis 1) Technical analysis is the use of past prices to guide trading decisions. 2) For about 15 years, people have been finding that technical trading rules make excess returns in the foreign exchange market. (Sweeney, 1986; 1988) (a) Moving average rules and filter rules. 3) The success of technical trading rules seems to contradict the efficient markets hypothesis. 6

C) Explanations for the success of technical analysis 1) Data mining 2) The returns to technical analysis are compensation for bearing risk (a) Measures of risk: Sharpe ratios, CAPM betas 3) Central bank intervention 7

III) What is genetic programming? A) GP is a variation of genetic algorithms 1) GA are due to Holland (1975) 2) Genetic algorithms are computer search procedures based on the principles of natural selection as originally expounded in Darwin's theory of evolution. B) GP is a similar search algorithm for spaces that consist of decision trees. 1) GP was developed by Koza (1992). 2) We can think of trading rules as decision trees. 8

IV) “Is Technical Analysis in the Foreign Exchange Market Profitable? A Genetic Programming Approach” Neely, Weller and Dittmar (1997) A) The data: daily exchange rates and interest rates. $/DM, $/¥, $/£, $/SF, DM/¥ and £/SF 1) Normalized by a 250 -day moving average B) The fitness criterion is the excess return over borrowing in one currency and investing in the other, each day. 9
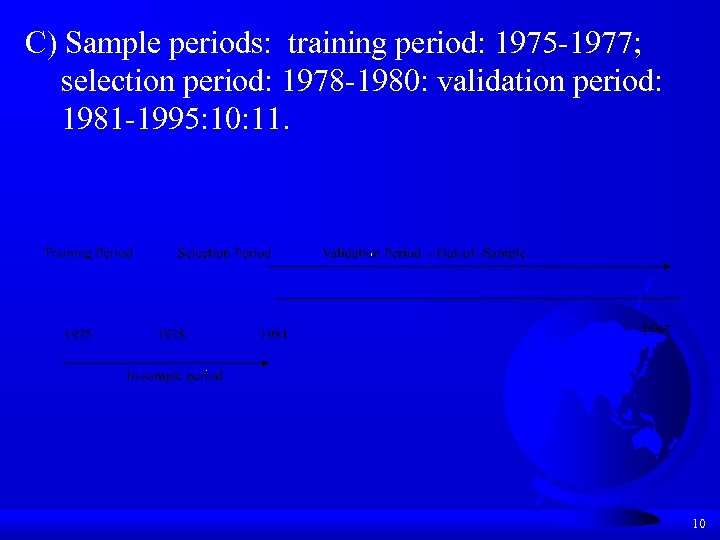
C) Sample periods: training period: 1975 -1977; selection period: 1978 -1980: validation period: 1981 -1995: 10: 11. 10
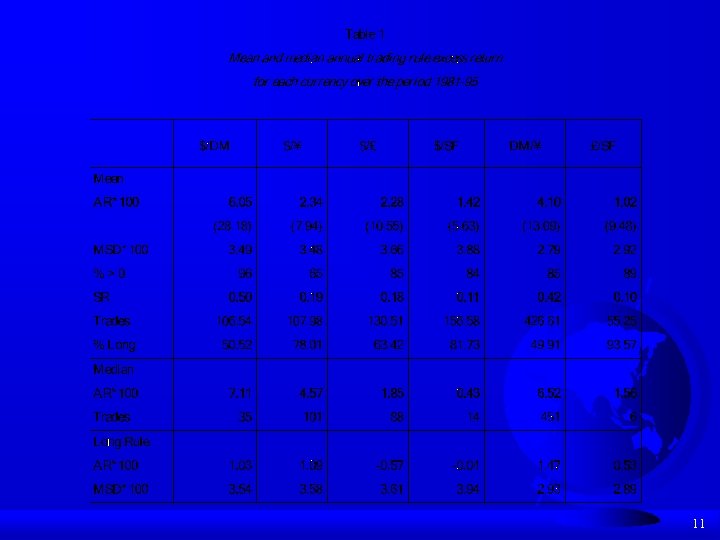
11

E) Structure of the rules 1) Rules were usually too complex to analyze by hand but those that were understandable had extrapolative features. 2) The 55 th best $/DM rule over the selection period, whose excess return was 7. 34, number of trades was 37 and correlation with the median rule was 0. 9911, prescribed: "Take a long position if the four-day minimum of the normalized exchange rate is greater than one. " F) Rules trained on $/DM data proved profitable on other exchange rates, out of sample. 12
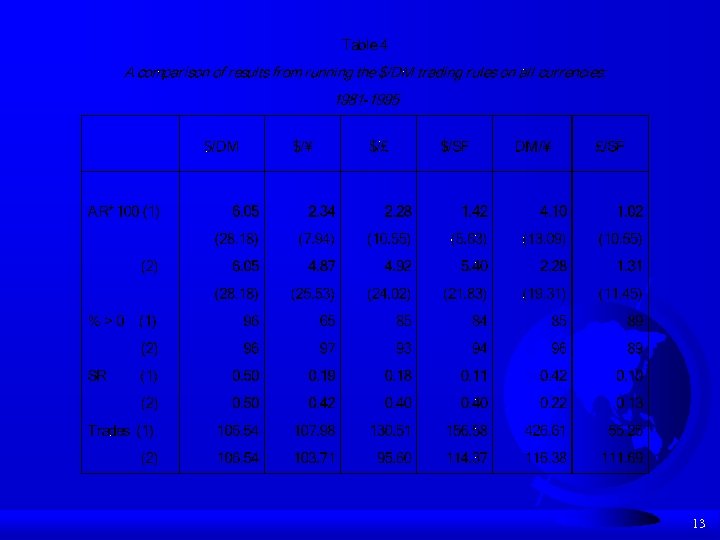
13

G) Transactions costs can aid in avoiding overfitting the data 1) Transactions costs were set at 0. 001 per round trip in the training/selection period, 0. 0005 in the validation period. H) Risk measures 1) Sharpe ratios were between 0. 1 and 0. 5. The S&P 500 Sharpe ratio was about 0. 3 over the same period 2) CAPM beta 14
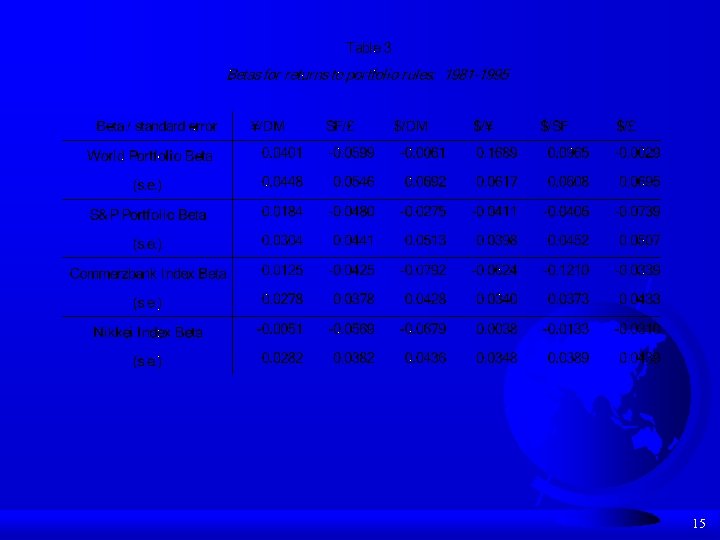
15

V) "Technical Trading Rules in the European Monetary System” -- Neely and Weller (1998) A) The Data and sample periods 1) Four ERM exchange rates: DEM/FRF, DEM/ITL, DEM/NLG and DEM/GBP 2) Training period, 3/13/79 to 1/2/83; selection period, 1/3/83 to 1/1/86; validation period, 1/2/86 to 6/21/96. 16
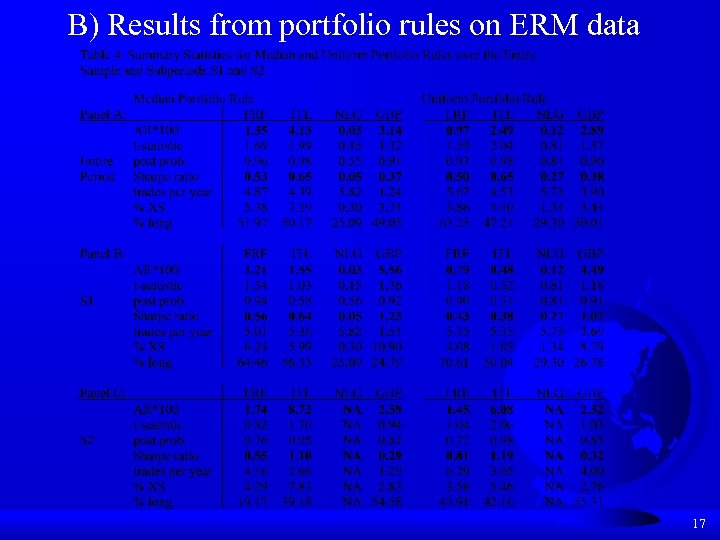
B) Results from portfolio rules on ERM data 17

C) Structure of the rules: The interest differential and not the past exchange rate series is the most important informational input to the trading rule. 1) Example: “Go long if the interest differential (British minus German) is greater than 4. 42 per cent. ” a) This simple rule was the 28 th best out-of-sample for the DEM/GBP, having an excess return of 3. 32 per cent per year and a correlation of 0. 95 with the median rule. 2) Moving average and filter rules did not do well. 3) High interest rate and mean reversion rules did not do well. 18
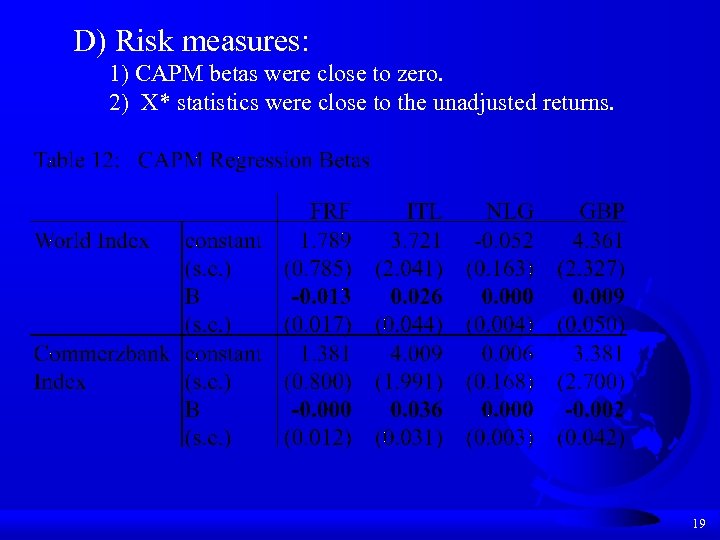
D) Risk measures: 1) CAPM betas were close to zero. 2) X* statistics were close to the unadjusted returns. 19

VI) “Technical Analysis and Central Bank Intervention” (Neely and Weller, 1998) A) An explanation for the success of TA B) There is previous work linking technical analysis and central bank intervention. C) Can CBI information improve an ex ante trading rule? D) Method: Supply intervention information as 1, 2, or 3 to the rule generating program. 20
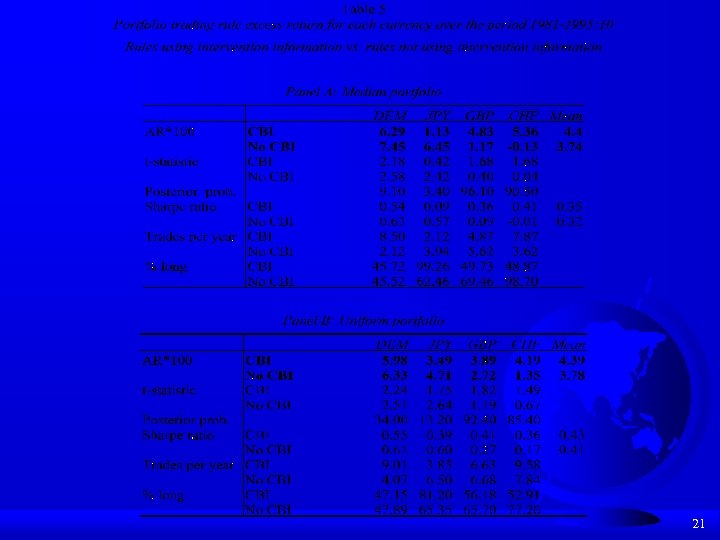
21
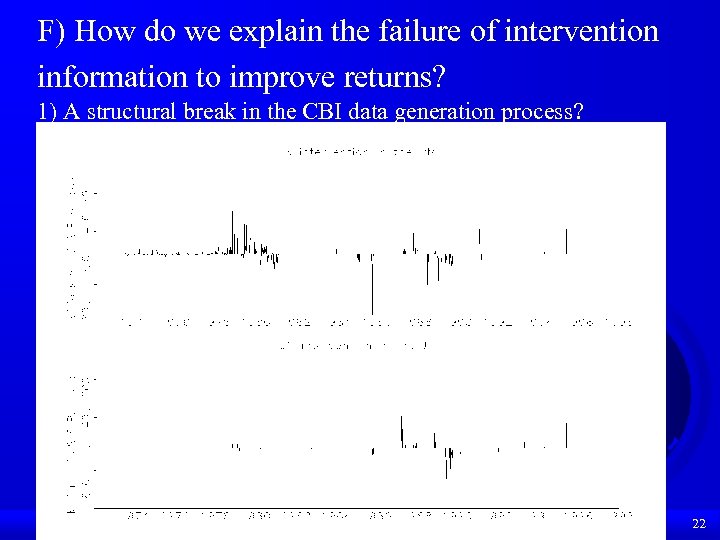
F) How do we explain the failure of intervention information to improve returns? 1) A structural break in the CBI data generation process? 22

VII) What do we learn about market efficiency from these exercises? A) The success of TA presents a puzzle to the EMH; the success of GP deepens this puzzle because GP provides a true, ex ante test of technical trading rules. B) There has been work on institutional constraints that may explain some lack of risk arbitrage. 23

C) There has been additional work on behavioral finance as a result of the success of TA. D) The success of TA underscores our need for a better understanding of risk. 24

VIII) Work in Progress A) High frequency trading rules B) Options pricing 1) HLP showed how neural networks could price and delta hedge options. We are exploring similar issues with GP. 25

The End 26
daeb31bd118d8ce8731602103f0e5653.ppt