What does calibration give An image line l

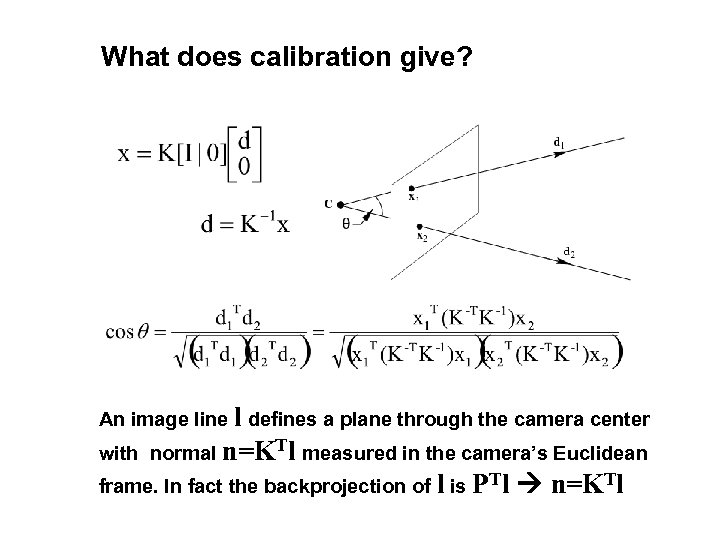
What does calibration give? An image line l defines a plane through the camera center with normal n=KTl measured in the camera’s Euclidean frame. In fact the backprojection of l is PTl n=KTl

The image of the absolute conic mapping between p∞ to an image is given by the planar homogaphy x=Hd, with H=KR absolute conic (IAC), represented by I 3 within p∞ (w=0) its image (IAC) (i) IAC depends only on intrinsics (ii) angle between two rays (iii) DIAC=w*=KKT (iv) w K (Cholesky factorization) (v) image of circular points belong to w (image of absolute conic)

A simple calibration device (i) compute Hi for each square (corners (0, 0), (1, 0), (0, 1), (1, 1)) (ii) compute the imaged circular points Hi [1, ±i, 0]T (iii) fit a conic w to 6 imaged circular points (iv) compute K from w=K-T K-1 through Cholesky factorization (= Zhang’s calibration method)

Orthogonality relation

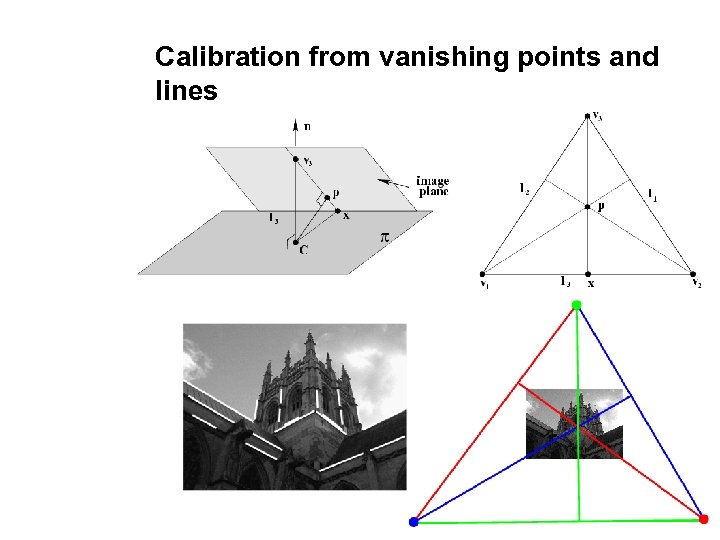
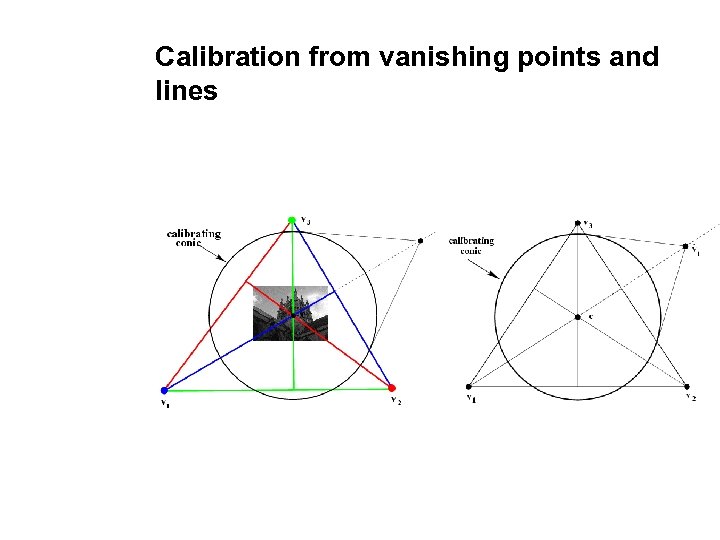
Calibration from vanishing points and lines

Two-view geometry Epipolar geometry F-matrix comp. 3 D reconstruction Structure comp.

Three questions: (i) Correspondence geometry: Given an image point x in the first view, how does this constrain the position of the corresponding point x’ in the second image? (ii) Camera geometry (motion): Given a set of corresponding image points {xi ↔x’i}, i=1, …, n, what are the cameras P and P’ for the two views? (iii) Scene geometry (structure): Given corresponding image points xi ↔x’i and cameras P, P’, what is the position of (their pre-image) X in space?

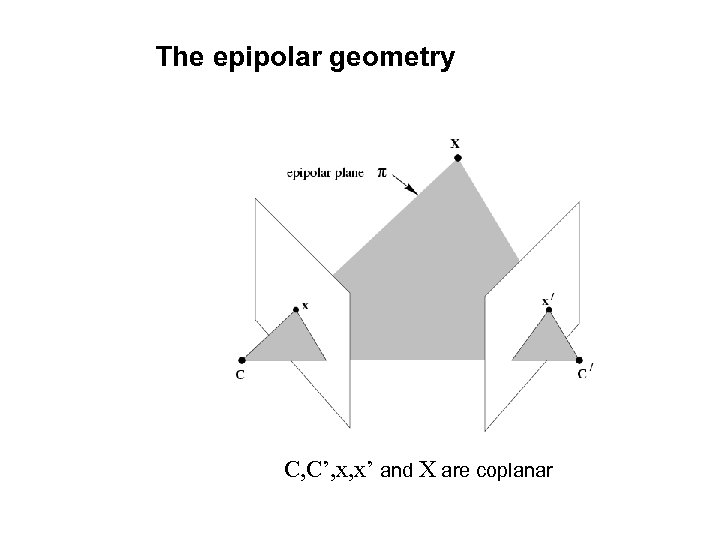
The epipolar geometry C, C’, x, x’ and X are coplanar

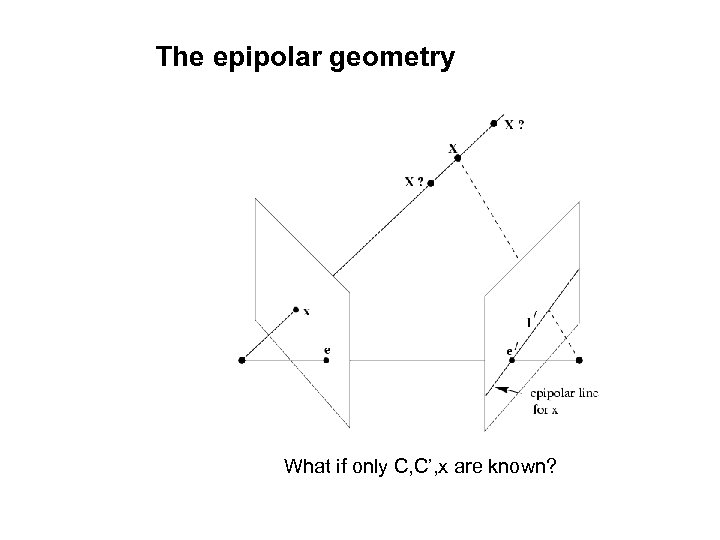
The epipolar geometry What if only C, C’, x are known?

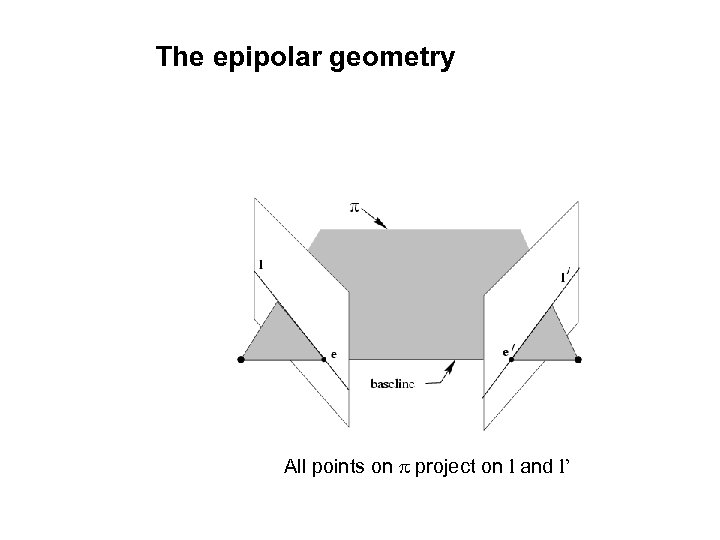
The epipolar geometry All points on p project on l and l’

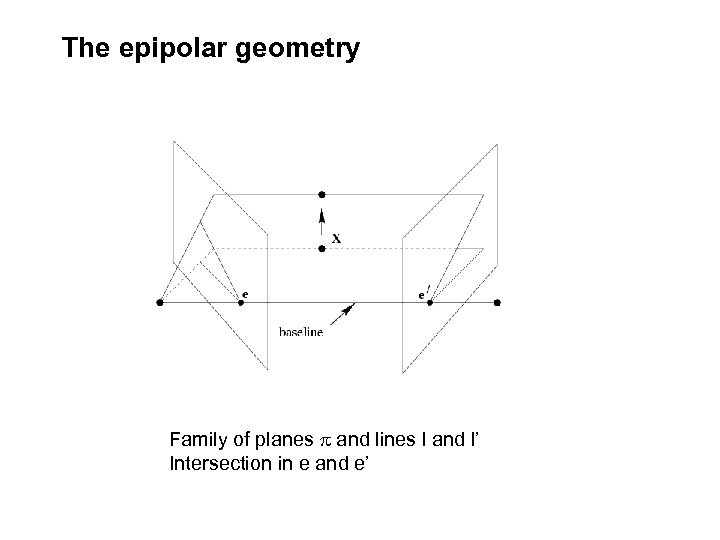
The epipolar geometry Family of planes p and lines l and l’ Intersection in e and e’

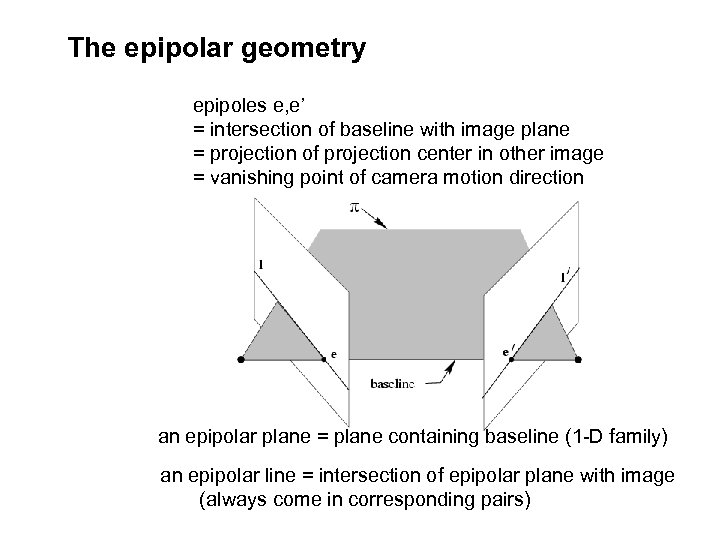
The epipolar geometry epipoles e, e’ = intersection of baseline with image plane = projection of projection center in other image = vanishing point of camera motion direction an epipolar plane = plane containing baseline (1 -D family) an epipolar line = intersection of epipolar plane with image (always come in corresponding pairs)

Example: converging cameras

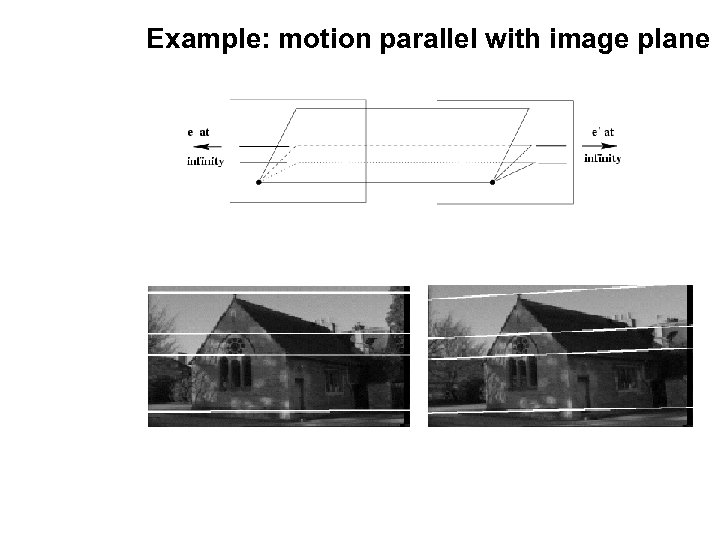
Example: motion parallel with image plane

The fundamental matrix F algebraic representation of epipolar geometry we will see that mapping is (singular) correlation (i. e. projective mapping from points to lines) represented by the fundamental matrix F

The fundamental matrix F algebraic derivation e’ is the image of C taken by the second camera

The fundamental matrix F correspondence condition The fundamental matrix satisfies the condition that for any pair of corresponding points x↔x’ in the two images

The fundamental matrix F F is the unique 3 x 3 rank 2 matrix that satisfies x’TFx=0 for all x↔x’ (i) Transpose: if F is fundamental matrix for (P, P’), then FT is fundamental matrix for (P’, P) (ii) Epipolar lines: l’=Fx & l=FTx’ (iii) Epipoles: on all epipolar lines, thus e’TFx=0, x e’TF=0, similarly Fe=0; (iv) e’ is left null space of F (v) F has 7 d. o. f. , i. e. 3 x 3 -1(homogeneous)-1(rank 2) (vi) F is a correlation, projective mapping from a point x to a line l’=Fx (not a proper correlation, i. e. not invertible)

Projective transformation and invariance Derivation based purely on projective concepts F invariant to transformations of projective 3 -space unique not unique canonical form

Projective ambiguity of cameras given F previous slide: at least projective ambiguity this slide: not more! ~~ Show that if F is same for (P, P’) and (P, P’), there exists a projective transformation H so that ~ ~ P=HP and P’=HP’ lemma: (22 -15=7, ok)

Canonical cameras given F F matrix corresponds to P, P’ iff P’TFP is skew-symmetric F matrix, S skew-symmetric matrix (fund. matrix=F) Possible choice: Canonical representation:

PROJECTIVE RECONSTRUCTION Computation of F 1 i Ransac: - 8 point correspondence samples Computation of canonical cameras from F 1 i Triangulation of points in 3 D -Compute viewing rays from cameras -Intersect viewing rays associated to corresponding points

The essential matrix ~fundamental matrix for calibrated cameras (remove K) 5 d. o. f. (3 for R; 2 for t up to scale) E is essential matrix if and only if two singularvalues are equal (and third=0) SVD

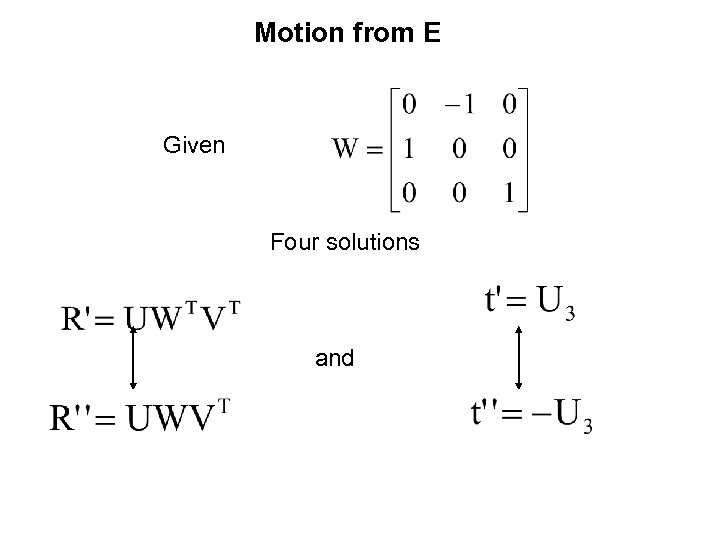
Motion from E Given Four solutions and

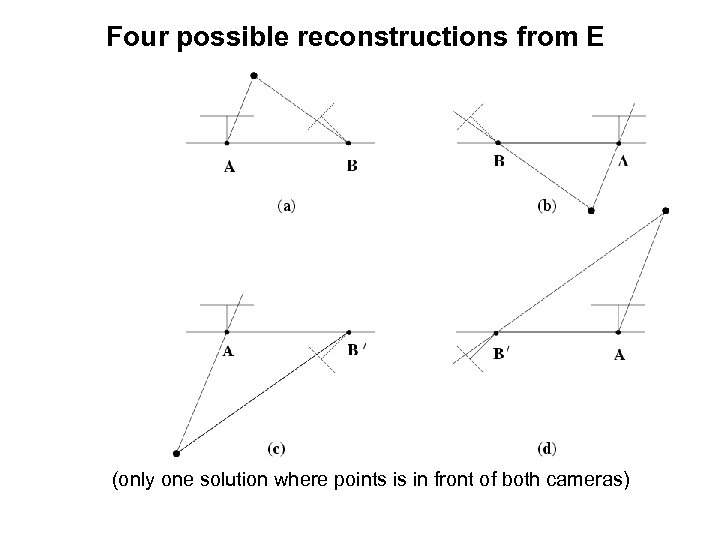
Four possible reconstructions from E (only one solution where points is in front of both cameras)

Self-calibration

Motivation • Avoid explicit calibration procedure – Complex procedure – Need for calibration object – Need to maintain calibration

Motivation • Allow flexible acquisition – No prior calibration necessary – Possibility to vary intrinsics – Use archive footage

Constraints ? • Scene constraints – Parallellism, vanishing points, horizon, . . . – Distances, positions, angles, . . . Unknown scene no constraints • Camera extrinsics constraints – Pose, orientation, . . . Unknown camera motion no constraints • Camera intrinsics constraints – Focal length, principal point, aspect ratio & skew Perspective camera model too general some constraints

Constraints on intrinsic parameters Constant e. g. fixed camera: Known e. g. rectangular pixels: square pixels: principal point known:

Self-calibration Upgrade from projective structure to metric structure using constraints on intrinsic camera parameters – Constant intrinsics (Faugeras et al. ECCV´ 92, Hartley´ 93, Triggs´ 97, Pollefeys et al. PAMI´ 98, . . . ) – Some known intrinsics, others varying (Heyden&Astrom CVPR´ 97, Pollefeys et al. ICCV´ 98, . . . ) – Constraints on intrincs and restricted motion (e. g. pure translation, pure rotation, planar motion) (Moons et al. ´ 94, Hartley ´ 94, Armstrong ECCV´ 96)

A counting argument • To go from projective (15 DOF) to metric (7 DOF) at least 8 constraints are needed • Minimal sequence length should satisfy • Independent of algorithm • Assumes general motion (i. e. not critical)

known internal parameters rectangular pixels square pixels

Same camera for all images same intrinsics same image of the absolute conic e. g. moving cameras given sufficient images there is in general only one conic that projects to the same image in all images, i. e. the absolute conic This approach is called self-calibration, see later transfer of IAC:

(a) Compute F from xi↔x‘i (b) Compute P, P‘ from F (c) Triangulate Xi from xi↔x‘i Obtain projective reconstruction (P, P‘, {Xi}) e. g.

The metric reconstruction will be t=0 Let the unknown plane at the infinity in the starting projective reconstruction be From

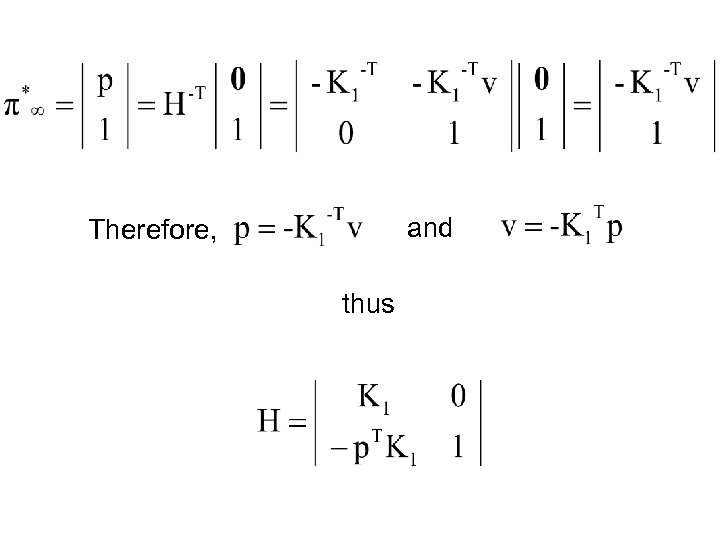
and Therefore, thus

Now Therefore, since Self-calibration equation 8 unknowns: and

Equations come from constraints on intrinsics: -known parameters (e. g. s=0 or square pixels) -fixed parameters (e. g. s, or aspect ratio) needed views: n, with Solution: nonlinear algorithms (Cipolla)

Uncalibrated visual odometry for ground plane motion (joint work with Simone Gasparini)

Problem formulation • Given: – an uncalibrated camera mounted on a robot – the camera is fixed and aims at the floor – the robot moving on a planar floor (ground plane) • Determine: – the estimate of robot motion from observed features on the floor

Technique involved Estimate the ground plane transformation (homography) between images taken before and after robot displacement

Motivations • Dead reckoning techniques are not reliable and diverge after few steps [Borenstein 96] • Visual odometry techniques exploits cameras to recover motion • We use a single uncalibrated camera – 3 D reconstruction with uncalibrated camera usually require auto-calibration – Non-planar motion is required [Triggs 98] – Planar motion with different camera attitudes [Knight 03] – Special devices is required (e. g. PTZ cameras)

Problem formulation • Fixed uncalibrated camera mounted on a robot • The pose of the camera w. r. t. the robot is unknown • The projective transformation between ground plane and image plane is a homography T (3 x 3) • T does not change with robot motion • T is uknown

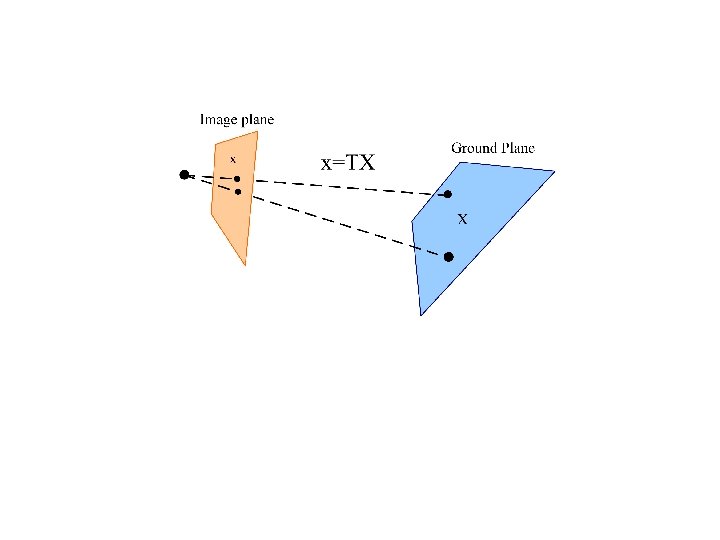
Problem formulation • Robot and camera undergo a planar motion – rotation of unknown angle q about unknown vertical axis – 2 D rotation matrix R (3 x 3 with homogeneous coordinates)

Problem formulation • Given 2 images before and after robot displacement determine: – Rotation centre C – Rotation angle q – Determine unknown transformation T between ground plane and image plane

Ground reference frame • We define a ground reference frame – O is the origin of the projected reference frame • E. g. O is the backprojection of image point O’(0, 0) – The vector connecting the origin to a point A is the unit vector along the x-axis • E. g. A is the backprojection of image point A’(100, 0)

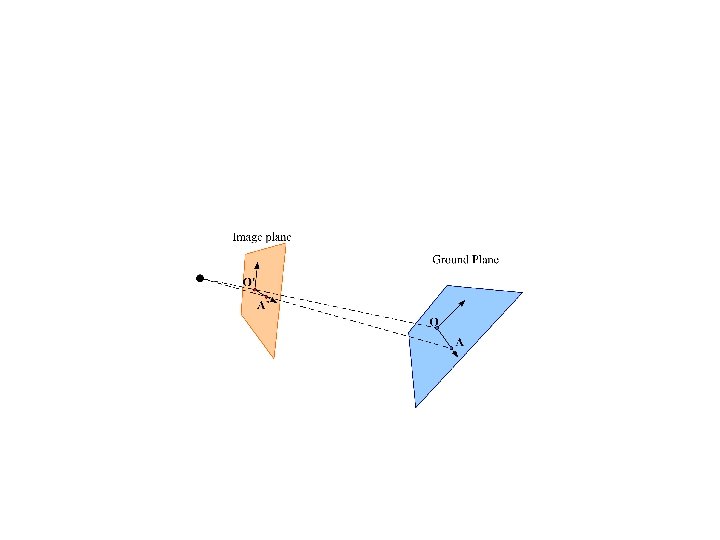
Estimation of robot displacement • Transformation relating the two images is still a homography • Eigenvectors of H:

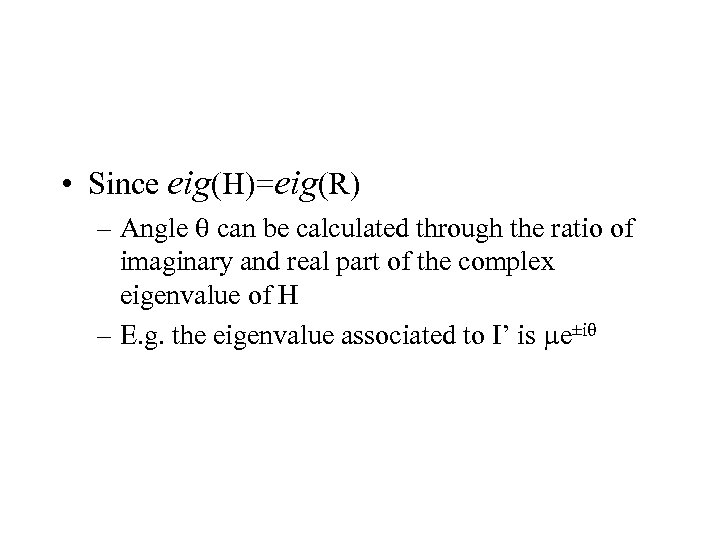
• Since eig(H)=eig(R) – Angle q can be calculated through the ratio of imaginary and real part of the complex eigenvalue of H – E. g. the eigenvalue associated to I’ is me±iq

Estimation of robot displacement: degenerate motion Pure translation: a frequent motion on planar floor • Under pure translation, the whole line at the infinity is invariant

ground plane can be only rectified modulo an affine transformation: e. g. , orientation of translaton wrt ground reference can not be determined • In practice: – Use a motion including rotations to estimate ground plane to image plane transformation T – Use knowledge of T while translating

Estimation of the transformation T • Estimating T allows to determine the shape of observed features • Four pairs of corresponding points are needed – The 2 circular points I and J – The 2 points A and O used for ground reference

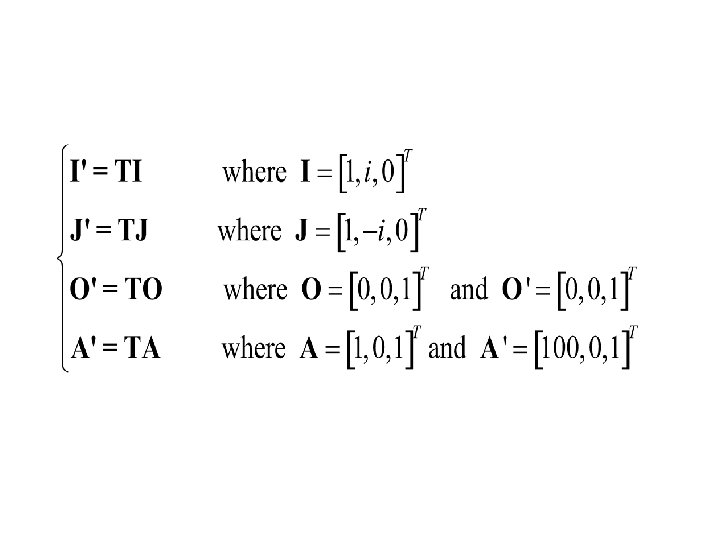
Experimental set up • Fixed perspective camera placed on turntable ( ground truth) • Optical distortion is negligible • Camera pointing towards the ground floor • Camera viewpoint in a generic position wrt rotation axis

• Basic algorithm: – Feature (corner) extraction from floor texture [Harris 88] – Feature tracking and matching in order to determine correspondences – Corresponding features used to fit the homography H – Eigendecomposition of matrix H • • Rotation angle Image of circular points Image of rotation centre Ground plane to image plane transformation

Experiments on sequences of images Sequence of large displacements • Image displacements of the order of 10° • Features extracted and matched [Torr 93]

• Use best matching pairs to fit a homography using RANSAC [Fischler 81] • Good overall accuracy (error < 1°) • Larger displacements affect matching

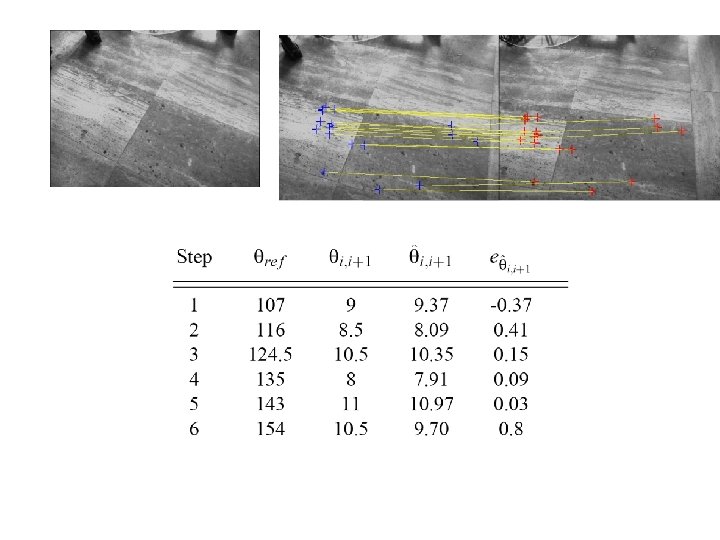
Experiments on sequences of images Sequence of small displacements • Image displacements of about 5° • Small rotations may lead to numerical instability • Track features over three images – H 13 fitted with correspondences of 1 and 3 • Good overall accuracy (error < 1°)

1 H 13 2 3

Experiments on a mobile platform Feature extraction and matching between images Rotation and relevant centre of rotation determination