adcc80431f91cea44920bf46e373687d.ppt
- Количество слайдов: 15

What are some problems with control of robot actions? Ø Joint play, compounded through N joints. Ø Accelerating masses produce vibration, elastic deformations in links. Ø Torques, stresses transmitted depending on end actuator loads. Ø Feedback loop creates instabilities. § Delay between sensing and reaction.

Let’s look at a simple robot. Ø Coordinates to describe position. § rectangular (x, y, z) § cylindrical (r, , z) § spherical (r, , ) Ø Frames to describe position. § World coordinate frame § Object frame x' x'' x Ø Want a way to transform from one coordinate system to another. § x” to x’ to x
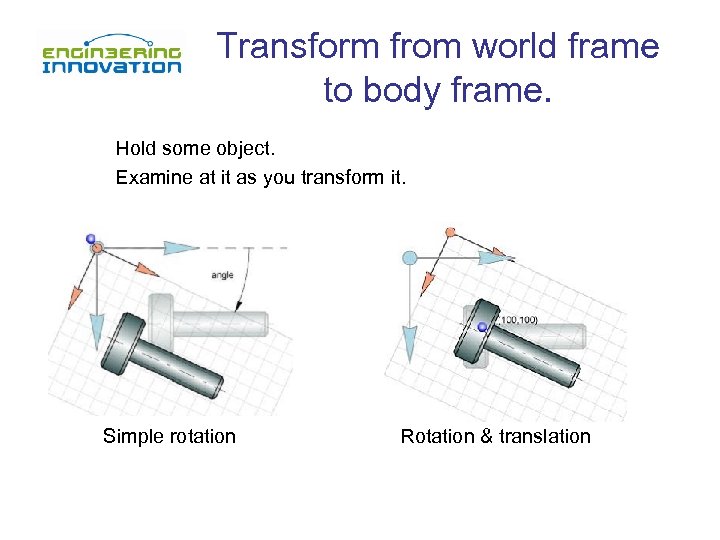
Transform from world frame to body frame. Hold some object. Examine at it as you transform it. Simple rotation Rotation & translation
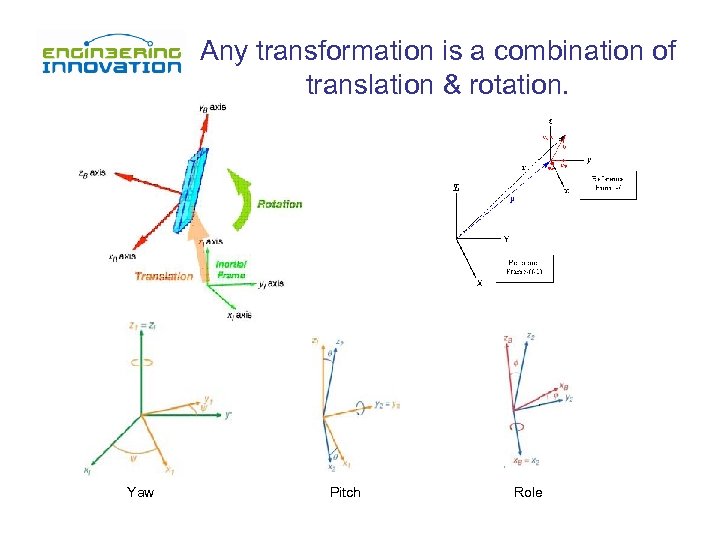
Any transformation is a combination of translation & rotation. Yaw Pitch Role

Mathematics of Transformations Ø General coordinate transformation from x’ to x is x = Bx’ + p , where B is a rotation matrix and p is a translation vector Ø More conveniently, one can create an augmented matrix which allows the above equation to be expressed as x = A x’. Ø Coordinate transformations of multilink systems are represented as x 0 = A 01 A 12 A 23. . . A(n-1)(n)xn
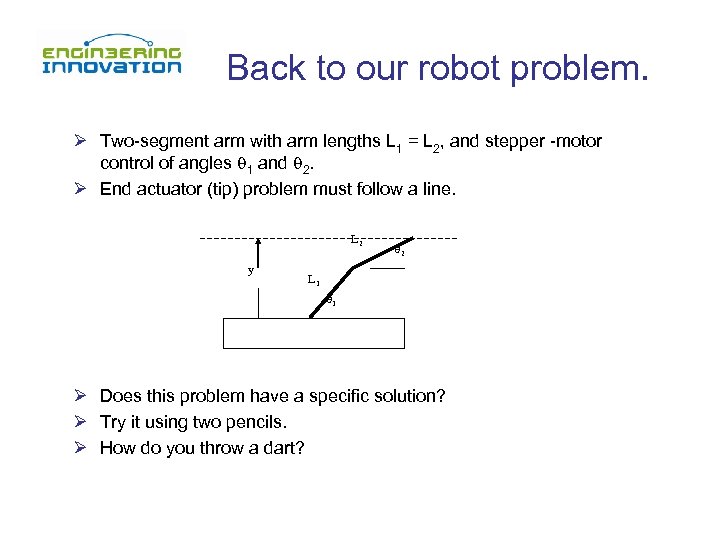
Back to our robot problem. Ø Two-segment arm with arm lengths L 1 = L 2, and stepper -motor control of angles 1 and 2. Ø End actuator (tip) problem must follow a line. L 2 y 2 L 1 1 Ø Does this problem have a specific solution? Ø Try it using two pencils. Ø How do you throw a dart?
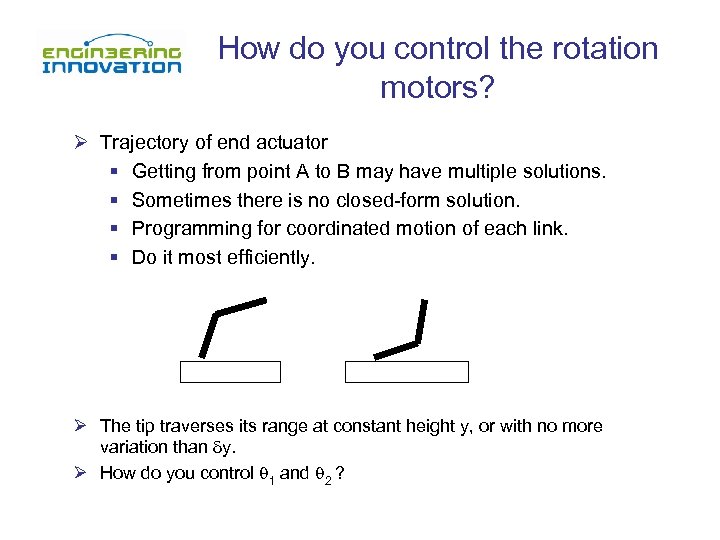
How do you control the rotation motors? Ø Trajectory of end actuator § Getting from point A to B may have multiple solutions. § Sometimes there is no closed-form solution. § Programming for coordinated motion of each link. § Do it most efficiently. Ø The tip traverses its range at constant height y, or with no more variation than y. Ø How do you control 1 and 2 ?

There is no closed-form solution to this problem. Ø Must use approximations, and accept some minor variations in y. Ø Moving the arm tip through its maximum range of x might have to be accomplished through a sequence of program steps. Ø Possible approaches: § Program the rates of change of 1 and 2 for y = const. for initial values of 1 and 2. When arm tip exceeds y, reprogram for new values of 1 and 2. § Program the rates of change of 1 and 2 at the initial point and at some other point for y = const. Take the average of these two rates, and hope that y is not exceeded. If it is exceeded, reprogram for a shorter distance. Continue program segments until the arm tip has traversed its range. § The rate of change of 1 and 2 can be changed in a programming segment, i. e. , the rates of change need not be uniform over time. This programming strategy incorporates approaches 1) and 2). Start with rates of change for the initial values of 1 and 2 , then add an acceleration component so that y = const. will also be satisfied at a distant position.

The derivative shows change of position. The position of arm tip is x = L 1 (cos 1 + cos 2) y = L 1 (sin 1 + sin 2) Arm tip moves by changing 1 and 2 as a function of time. Therefore So, as 1 and 2 are changed, x and y are affected. To satisfy y = constant, we must have So the rates at which 1 and 2 are changed depend on the values of 1 and 2.

How do you measures of performance of robot? Ø Speed and acceleration Ø Ø Resolution Working volume Accuracy Cost

The Future of Robotics. Ø Robots that can learn. Ø Robots with artificial intelligence. Ø Robots that make other robots.

Will robots take over the world? Ø Which decisions can the machine make without human supervision? Ø May machine-intelligent systems make mistakes (at the same level as humans)? Ø May intelligent systems gamble when uncertain (as humans do)? Ø Can (or Should) intelligent systems exhibit "personality”? Ø Can (or Should) intelligent systems express "emotion”? Ø How much information should the machine display to the human operator? HAL - 2001 Space Odyssey

Play Robot Constructor Ø http: //www. channel 4. com/science/microsites/R/robo ts/constructor. html
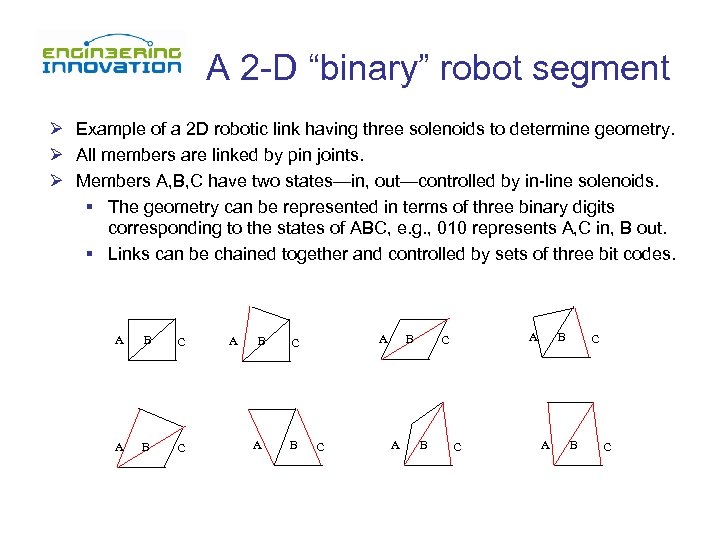
A 2 -D “binary” robot segment Ø Example of a 2 D robotic link having three solenoids to determine geometry. Ø All members are linked by pin joints. Ø Members A, B, C have two states—in, out—controlled by in-line solenoids. § The geometry can be represented in terms of three binary digits corresponding to the states of ABC, e. g. , 010 represents A, C in, B out. § Links can be chained together and controlled by sets of three bit codes. A B C A B A A C B C B A C B C

How are robots different from automated machinery? Ø Machinery is designed to carry out a specific task. § Bottling machine § Dishwasher § Paint sprayer Ø Robots are designed to carry out a variety of tasks § Pick and place arms § Mobile robots § Computer Numerical Control machines Ø The lines are becoming blurred.
adcc80431f91cea44920bf46e373687d.ppt