4755d3ca17768c2ce79938af92cd261a.ppt
- Количество слайдов: 25

WEMBA 2000 Real Options 1 What is an Option? Definitions: An option is an agreement between two parties that gives the purchaser of the option the right, but not the obligation, to buy or sell a specific quantity of an asset at a specified price during a designated time period. A Call is the right to purchase the underlying asset A Put is the right to sell the asset The Strike Price is the pre-specified price at which the option holder can buy (in the case of a call) or sell (in the case of a put) the asset to the option seller The Expiration date is the date (and time) after which the option expires The Notional Amount is the quantity of the underlying asset that the option buyer has the right to buy or sell under the terms of the option contract The Premium is the price of the option contract (the amount paid by the buyer to the seller). The option buyer’s maximum “downside” (possible loss) is the amount of the premium. Option premia are quoted as percentage of notional amount. To Exercise means to invoke the right to buy or sell the underlying asset under the terms of the option contract The Seller (or Writer) of the option receives a payment (the Option Premium) that then obligates him to sell (in the case of a call) or buy (in the case of a put) the asset.
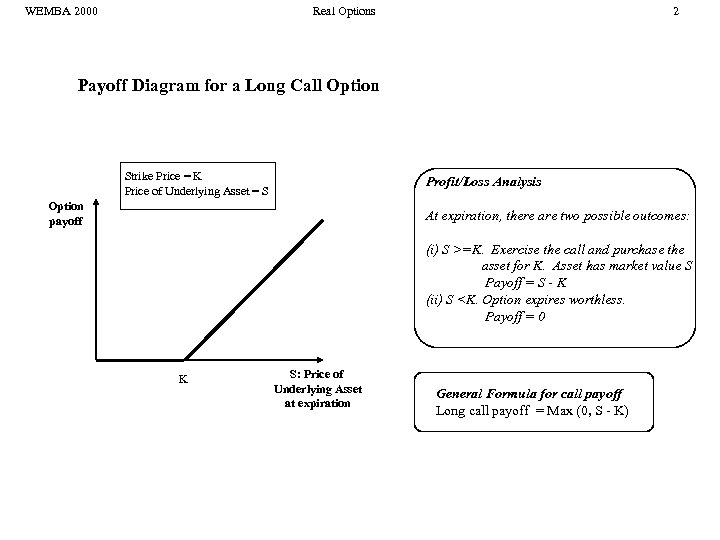
WEMBA 2000 Real Options 2 Payoff Diagram for a Long Call Option Strike Price = K Price of Underlying Asset = S Profit/Loss Analysis Option payoff At expiration, there are two possible outcomes: (i) S >=K. Exercise the call and purchase the asset for K. Asset has market value S Payoff = S - K (ii) S <K. Option expires worthless. Payoff = 0 K S: Price of Underlying Asset at expiration General Formula for call payoff Long call payoff = Max (0, S - K)
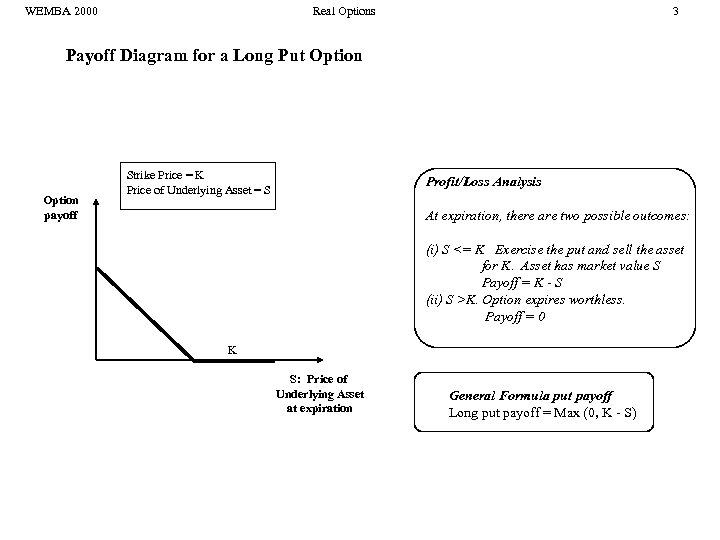
WEMBA 2000 Real Options 3 Payoff Diagram for a Long Put Option payoff Strike Price = K Price of Underlying Asset = S Profit/Loss Analysis At expiration, there are two possible outcomes: (i) S <= K Exercise the put and sell the asset for K. Asset has market value S Payoff = K - S (ii) S >K. Option expires worthless. Payoff = 0 K S: Price of Underlying Asset at expiration General Formula put payoff Long put payoff = Max (0, K - S)
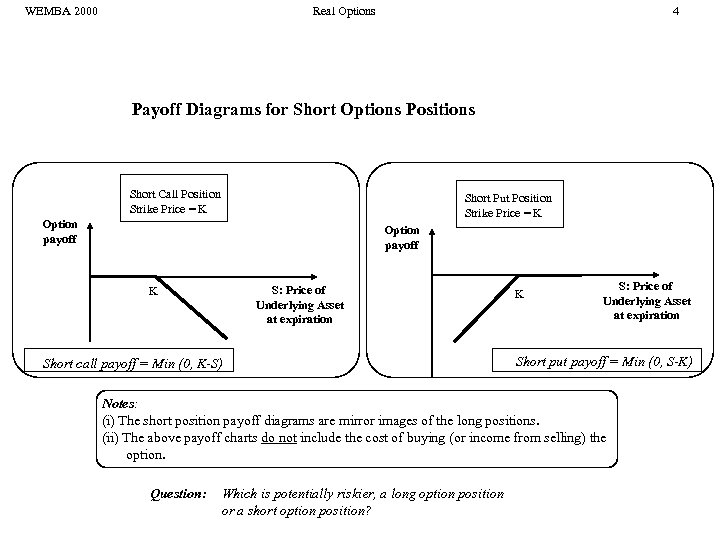
WEMBA 2000 Real Options 4 Payoff Diagrams for Short Options Positions Short Call Position Strike Price = K Short Put Position Strike Price = K Option payoff S: Price of Underlying Asset at expiration K Short call payoff = Min (0, K-S) K S: Price of Underlying Asset at expiration Short put payoff = Min (0, S-K) Notes: (i) The short position payoff diagrams are mirror images of the long positions. (ii) The above payoff charts do not include the cost of buying (or income from selling) the option. Question: Which is potentially riskier, a long option position or a short option position?
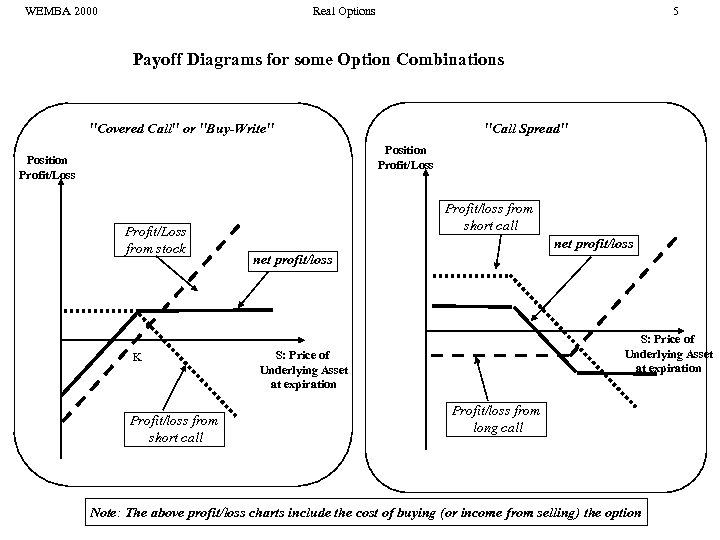
WEMBA 2000 Real Options 5 Payoff Diagrams for some Option Combinations "Covered Call" or "Buy-Write" "Call Spread" Position Profit/Loss from stock K Profit/loss from short call net profit/loss S: Price of Underlying Asset at expiration Profit/loss from long call Note: The above profit/loss charts include the cost of buying (or income from selling) the option

WEMBA 2000 Real Options Factors that Influence Option Prices The six variablesthat affect option prices: 1. Current (spot) price on the underlying security 2. Strike price 3. Time to expiration 4. Implied (expected) volatility on the underlying security 5. The riskfree rate over the time period of the option 6. Any dividends or other cashflows that will be paid or received on the underlying asset during the life of the option 6

WEMBA 2000 Real Options 7 Valuation of Options: Put-Call Parity We construct two portfolios and show they always have the same payoffs, hence they must cost the same amount. Portfolio 1: Buy 1 share of the stock today for price S 0 and borrow an amount PV(X) = X e-r. T How much will this portfolio be worth at time T ? Cashflow Time = 0 Position Cashflow Time = T Buy Stock -S 0 ST Borrow PV(K) -K Net: Portfolio 1 Portfolio payoff at time T PV(K) - S 0 ST - K S Payoff from stock net payoff K -K Payoff from borrowing ST

WEMBA 2000 Real Options 8 Valuation of Options: Put-Call Parity Portfolio 2: Buy 1 call option and sell 1 put option with the same maturity date T and the same strike price K. How much will this portfolio be worth at time T ? Position Cashflow Time = 0 Buy Call -c Sell Put p Cashflow: Time = T ST < K ST > K Net: Portfolio 2 Portfolio payoff at time T 0 ST - K - (K - ST ) 0 ST - K p-c Payoff on long call net payoff K -K Payoff on short put ST

WEMBA 2000 Real Options 9 Valuation of Options: Put-Call Parity Payoff from Portfolio 1 and Portfolio 2 is the same, regardless of level of ST , hence cost of both portfolios (cashflows at time T = 0 ) must be the same. Hence: S 0 - PV(K) = c - p Put-Call Parity Rearranging: c = p + S 0 - PV(K) (1) Put-Call parity: a worked example Stock is selling for $100. A call option with strike price $90 and maturity 3 months has a price of $12. A put option with strike price $90 and maturity 3 months has a price of $2. The risk-free rate is 5%. Question: Is there an arbitrage? Test Put-Call parity: Right-hand side of (1): p + S 0 - PV(K) = 2 + 100 - 90 e -0. 05*0. 25 = 13. 12 Left-hand side of (1): c = 12 13. 12 ! Market Price of c is too low relative to the other three. Buy the call, and Sell the "replicating portfolio".
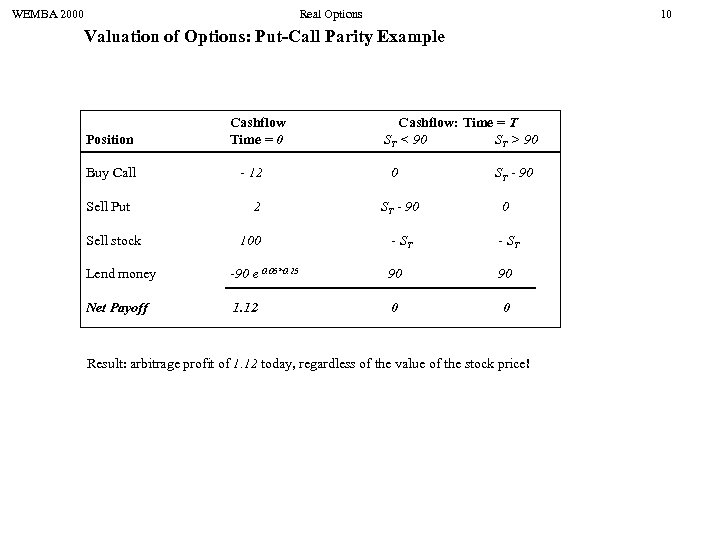
WEMBA 2000 Real Options 10 Valuation of Options: Put-Call Parity Example Position Buy Call Sell Put Sell stock Cashflow Time = 0 - 12 2 100 Cashflow: Time = T ST < 90 ST > 90 0 ST - 90 0 - ST Lend money -90 e 0. 05*0. 25 90 90 Net Payoff 1. 12 0 0 Result: arbitrage profit of 1. 12 today, regardless of the value of the stock price!

WEMBA 2000 Real Options 11 Valuation of Options: Black-Scholes Formula for Calls and Puts S = Current stock price K = Strike price on the option T = Time to maturity of the option in years (e. g. 5 months = 5/12 = 0. 417) r = Riskfree rate of interest = Expected ("Implied") volatility (standard deviation) of the underlying stock over the life of the option Black-Scholes Call Price c = S N( d 1 ) - X e -r. T N( d 2 ) (2) where: d 1 = ln (S/k) + (r + 2 / 2) T T d 2 = d 1 - T N(d ) = cumulative standard normal probability of value less than d Black-Scholes Put Price p = X e -r. T N( - d 2 ) - S N( - d 1 ) (3)

WEMBA 2000 Real Options 12 Valuation of Options: Black-Scholes Formula for Calls and Puts Example: Options on Compaq stock On Dec 20, Compaq stock closed at $76. 75 3 month riskfree rate: 5. 5% (e. g. yield on 3 month T-bill) Estimated volatility: 41% What are the values of 3 month call and put options with Strike = $75 ? Black-Scholes formula inputs and calculations: Observed inputs: Option contract inputs: S = 76. 75 r = 5. 5% K = 75 T = 0. 25 Estimated input (the future level of volatility is not observable) = 41% d 1 = [ ln (76. 75/75) + (0. 055 + 0. 412 / 2) 0. 25 ] 0. 41 0. 25 = 0. 2821 d 2 = d 1 - T = 0. 0771 N(d 1) = 0. 6111 N(d 2) = 0. 5307 [obtained from Excel "normsdist" function] c = 7. 638 p = 4. 864 [from equation (2) ] [from equation (3) ]
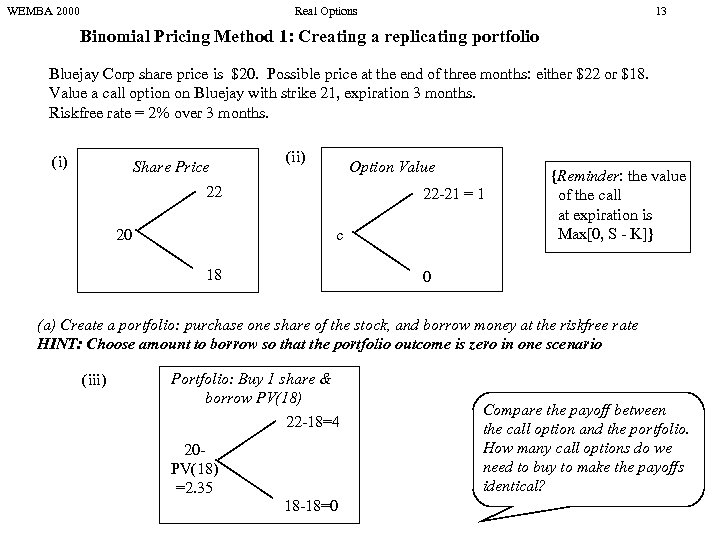
WEMBA 2000 Real Options 13 Binomial Pricing Method 1: Creating a replicating portfolio Bluejay Corp share price is $20. Possible price at the end of three months: either $22 or $18. Value a call option on Bluejay with strike 21, expiration 3 months. Riskfree rate = 2% over 3 months. (i) Share Price (ii) Option Value 22 20 22 -21 = 1 c 18 {Reminder: the value of the call at expiration is Max[0, S - K]} 0 (a) Create a portfolio: purchase one share of the stock, and borrow money at the riskfree rate HINT: Choose amount to borrow so that the portfolio outcome is zero in one scenario (iii) Portfolio: Buy 1 share & borrow PV(18) 22 -18=4 20 PV(18) =2. 35 18 -18=0 Compare the payoff between the call option and the portfolio. How many call options do we need to buy to make the payoffs identical?
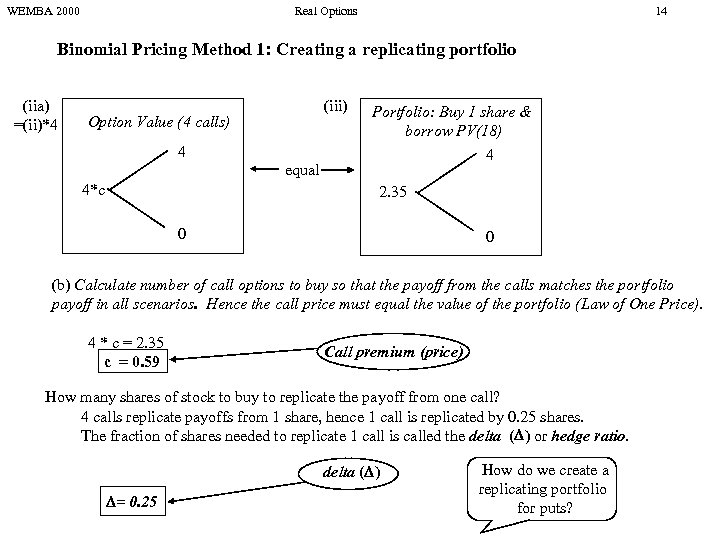
WEMBA 2000 Real Options 14 Binomial Pricing Method 1: Creating a replicating portfolio (iia) =(ii)*4 (iii) Option Value (4 calls) 4 equal 4*c Portfolio: Buy 1 share & borrow PV(18) 4 2. 35 0 0 (b) Calculate number of call options to buy so that the payoff from the calls matches the portfolio payoff in all scenarios. Hence the call price must equal the value of the portfolio (Law of One Price). 4 * c = 2. 35 c = 0. 59 Call premium (price) How many shares of stock to buy to replicate the payoff from one call? 4 calls replicate payoffs from 1 share, hence 1 call is replicated by 0. 25 shares. The fraction of shares needed to replicate 1 call is called the delta ( ) or hedge ratio. delta ( ) = 0. 25 How do we create a replicating portfolio for puts?
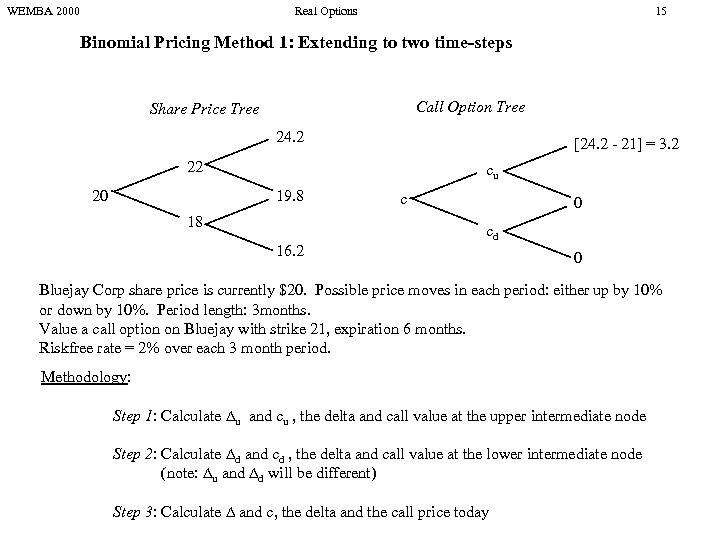
WEMBA 2000 Real Options 15 Binomial Pricing Method 1: Extending to two time-steps Call Option Tree Share Price Tree 24. 2 [24. 2 - 21] = 3. 2 22 20 cu 19. 8 18 16. 2 c 0 cd 0 Bluejay Corp share price is currently $20. Possible price moves in each period: either up by 10% or down by 10%. Period length: 3 months. Value a call option on Bluejay with strike 21, expiration 6 months. Riskfree rate = 2% over each 3 month period. Methodology: Step 1: Calculate u and cu , the delta and call value at the upper intermediate node Step 2: Calculate d and cd , the delta and call value at the lower intermediate node (note: u and d will be different) Step 3: Calculate and c, the delta and the call price today
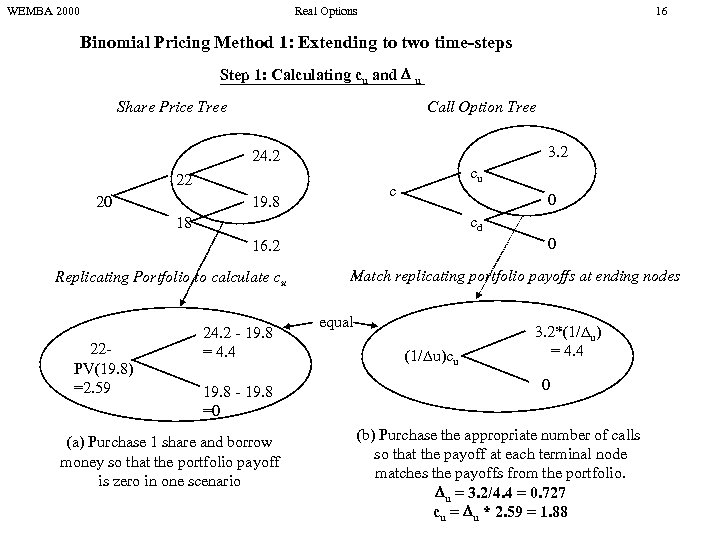
WEMBA 2000 Real Options 16 Binomial Pricing Method 1: Extending to two time-steps Step 1: Calculating cu and u Share Price Tree Call Option Tree 3. 2 24. 2 22 20 cu c 19. 8 0 cd 18 0 16. 2 Replicating Portfolio to calculate cu 22 PV(19. 8) =2. 59 24. 2 - 19. 8 = 4. 4 19. 8 - 19. 8 =0 (a) Purchase 1 share and borrow money so that the portfolio payoff is zero in one scenario Match replicating portfolio payoffs at ending nodes equal (1/ u)cu 3. 2*(1/ u) = 4. 4 0 (b) Purchase the appropriate number of calls so that the payoff at each terminal node matches the payoffs from the portfolio. u = 3. 2/4. 4 = 0. 727 cu = u * 2. 59 = 1. 88
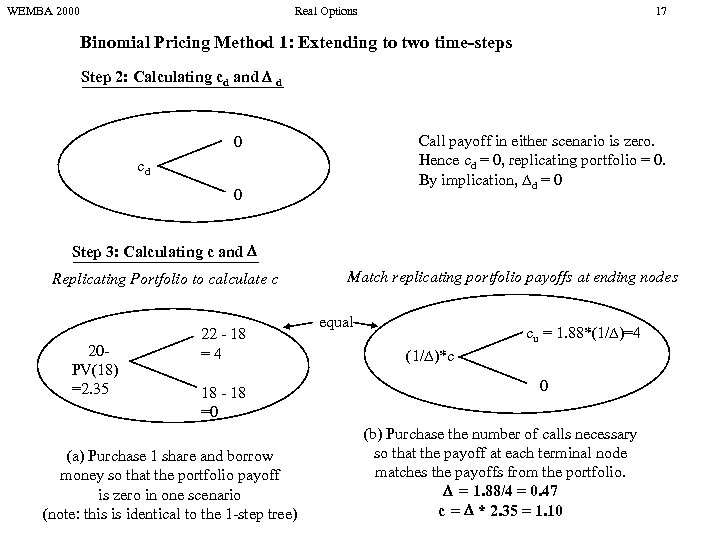
WEMBA 2000 Real Options 17 Binomial Pricing Method 1: Extending to two time-steps Step 2: Calculating cd and d Call payoff in either scenario is zero. Hence cd = 0, replicating portfolio = 0. By implication, d = 0 0 cd 0 Step 3: Calculating c and Replicating Portfolio to calculate c 20 PV(18) =2. 35 22 - 18 =4 18 - 18 =0 (a) Purchase 1 share and borrow money so that the portfolio payoff is zero in one scenario (note: this is identical to the 1 -step tree) Match replicating portfolio payoffs at ending nodes equal cu = 1. 88*(1/ )=4 (1/ )*c 0 (b) Purchase the number of calls necessary so that the payoff at each terminal node matches the payoffs from the portfolio. = 1. 88/4 = 0. 47 c = * 2. 35 = 1. 10
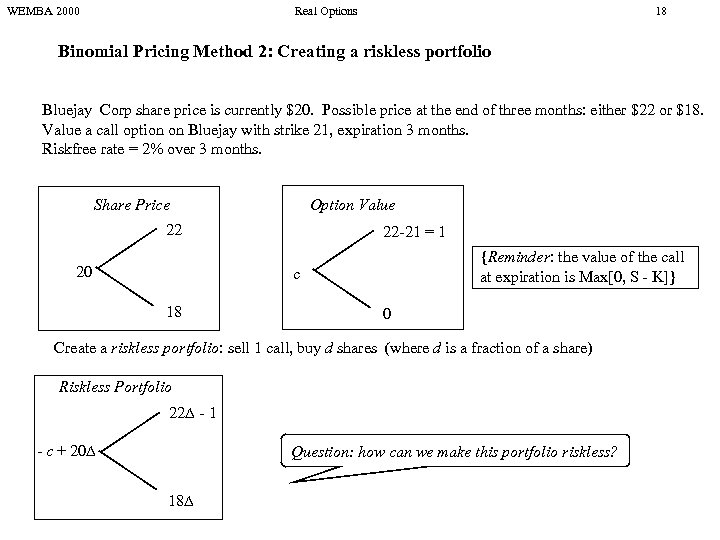
WEMBA 2000 Real Options 18 Binomial Pricing Method 2: Creating a riskless portfolio Bluejay Corp share price is currently $20. Possible price at the end of three months: either $22 or $18. Value a call option on Bluejay with strike 21, expiration 3 months. Riskfree rate = 2% over 3 months. Share Price Option Value 22 20 22 -21 = 1 {Reminder: the value of the call at expiration is Max[0, S - K]} c 18 0 Create a riskless portfolio: sell 1 call, buy d shares (where d is a fraction of a share) Riskless Portfolio 22 - 1 - c + 20 Question: how can we make this portfolio riskless? 18

WEMBA 2000 Real Options Binomial Pricing Method 2: Creating a riskless portfolio Riskless Portfolio 22 - 1 For the portfolio to be riskless, the two outcomes must have identical values. -c + 20 18 HINT: Choose so that: 22 - 1 = 18 Portfolio "delta" = 0. 25 Portfolio Terminal value = 4. 5 (in either scenario) Portfolio Present value = 4. 5/(1. 02) = 4. 41 (discount at riskfree rate) Hence: 4. 41 = -c + 20 c = 0. 59 Call premium (price) Note: this is the same call price and delta that we obtained using method 1. 19

WEMBA 2000 Real Options 20 Binomial Pricing Method 2: Creating a riskless portfolio Stock Price Option Value q 1 q 22 20 0. 59 1 -q Call price q 1 -q 0 = 0. 59 = [1 * q + 0 * (1 - q)]/1. 02 = 0. 6 18 Stock price = 20 = [22 * q + 18 * (1 - q)]/1. 02 q = 0. 6 What does the value q represent? It does not represent the probability that the stock price will move up or down! It is sometimes referred to as the “risk-neutral” probability that the stock price will move up or down.

WEMBA 2000 Real Options 21 Binomial Pricing Method 2: Generalization *Share Price Option Value Su cu + S c Sd Portfolio Su - cu = S-c Sd - cd cd For portfolio to be riskless, choose so that Su - cu = Sd - cd hence = cu - cd Su - Sd (1) Now the riskless terminal value, discounted at the riskless rate rf , should equal the portfolio cost: Su - cu = S - c (1 + rf ) Substitute for from (1): where c = q cu + (1 -q)cd (1 + rf ) (2) q = (1 + rf) - d (u - d) (3)
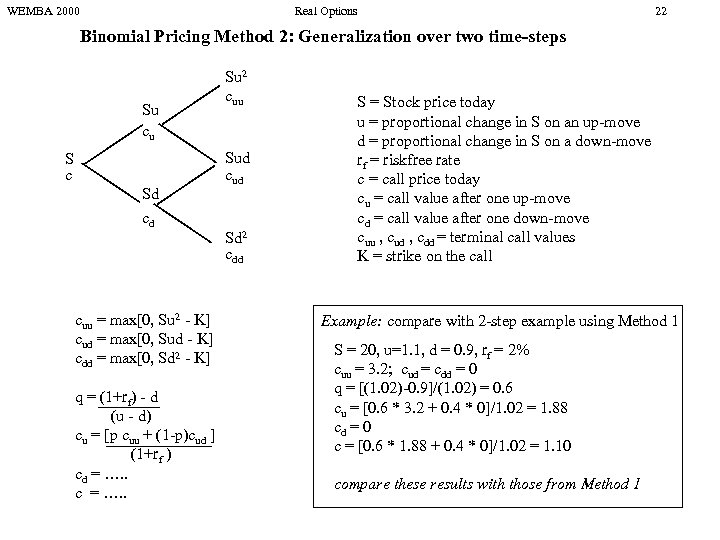
WEMBA 2000 Real Options 22 Binomial Pricing Method 2: Generalization over two time-steps Su cu S c Sd cd cuu = max[0, Su 2 - K] cud = max[0, Sud - K] cdd = max[0, Sd 2 - K] q = (1+rf) - d (u - d) cu = [p cuu + (1 -p)cud ] (1+rf ) cd = …. . c = …. . Su 2 cuu Sud cud Sd 2 cdd S = Stock price today u = proportional change in S on an up-move d = proportional change in S on a down-move rf = riskfree rate c = call price today cu = call value after one up-move cd = call value after one down-move cuu , cud , cdd = terminal call values K = strike on the call Example: compare with 2 -step example using Method 1 S = 20, u=1. 1, d = 0. 9, rf = 2% cuu = 3. 2; cud = cdd = 0 q = [(1. 02)-0. 9]/(1. 02) = 0. 6 cu = [0. 6 * 3. 2 + 0. 4 * 0]/1. 02 = 1. 88 cd = 0 c = [0. 6 * 1. 88 + 0. 4 * 0]/1. 02 = 1. 10 compare these results with those from Method 1

WEMBA 2000 Real Options 23 Valuation of Options: Binomial Pricing Method What have we shown? We can evaluate a call option either by creating a replicating portfolio of the underlying stock and borrowing, or by creating a riskless portfolio of the call and the underlying stock The two methods yield identical results What other information do we obtain from these methods? The delta or hedge ratio: the fraction of the underlying stock that we need to purchase relative to selling a single call option to obtain a riskless portfolio The risk-neutral probability of an upmove or downmove in the underlying stock What are the underlying assumptions of these methods? That we can freely buy and sell the underlying stock without transactions costs That we can borrow or lend money at the riskless rate of interest What are the limitations of these methods? They become very complex over a large number of steps (although computers can help) What is the connection between these methods and the Black-Scholes formula? The Black-Scholes formula effectively represents the binomial tree model over many hundreds or thousands of periods Binomial Tree methodology: Option price = delta * share price - bank loan Black Scholes formula: Option price = N(d 1 )* S - N(d 2)* PV(K)
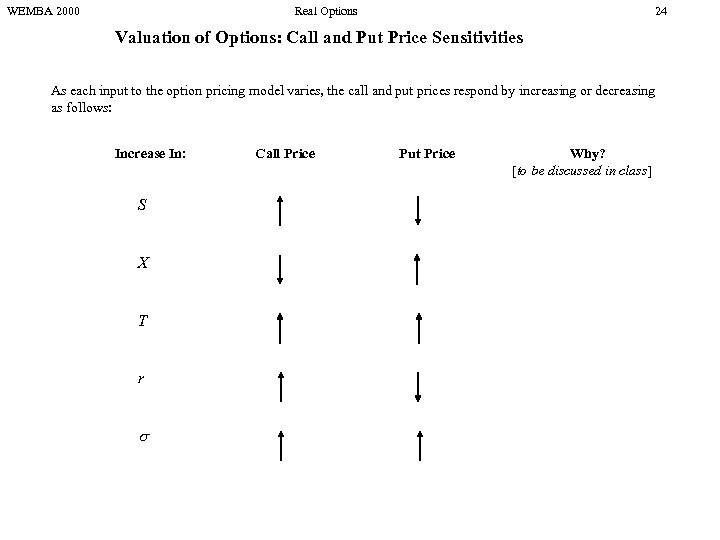
WEMBA 2000 Real Options 24 Valuation of Options: Call and Put Price Sensitivities As each input to the option pricing model varies, the call and put prices respond by increasing or decreasing as follows: Increase In: S X T r Call Price Put Price Why? [to be discussed in class]
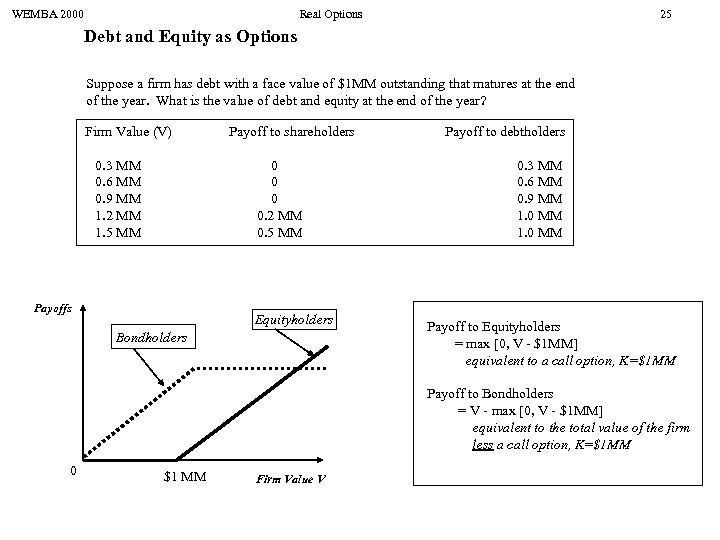
WEMBA 2000 Real Options 25 Debt and Equity as Options Suppose a firm has debt with a face value of $1 MM outstanding that matures at the end of the year. What is the value of debt and equity at the end of the year? Firm Value (V) 0. 3 MM 0. 6 MM 0. 9 MM 1. 2 MM 1. 5 MM Payoff to shareholders 0 0. 2 MM 0. 5 MM Payoffs Equityholders Bondholders Payoff to debtholders 0. 3 MM 0. 6 MM 0. 9 MM 1. 0 MM Payoff to Equityholders = max [0, V - $1 MM] equivalent to a call option, K=$1 MM Payoff to Bondholders = V - max [0, V - $1 MM] equivalent to the total value of the firm less a call option, K=$1 MM 0 $1 MM Firm Value V
4755d3ca17768c2ce79938af92cd261a.ppt