Welkom Klik linksonder op de xx knop om

Welkom Klik linksonder op de xx knop om te beginnen. Samengestelde interest Klik op de groene knop om verder te gaan.

Woord vooraf. Deze presentatie gaat over samengestelde interest. Er wordt kennis verondersteld van enkelvoudige interest en enige basiskennis van het gebruik van de TI-83 en het werken met Excel. Het is aan te bevelen pen en papier en je GRM bij de hand te hebben. Aan deze presentatie zijn een aantal oefenbestanden met open vragen gekoppeld: Oefenen met eindwaarde Oefenen met samengestelde interest Wil je je kennis nu al testen, klik dan op de betreffende toets.

Inhoudsopgave q Eindwaarde bij samengestelde interest § Interestfactor § Berekening interestbedrag § Rekenen met datums 10 q Contante waarde bij samengestelde interest 16 q Interest over delen van een periode en berekening wvovereenkomstig interestpercentage 23 q Overzicht belangrijkste regels 32 q Extra onderwerp: berekeningen met behulp van Excel 34 Klik op het onderwerp om er direct heen te gaan en op de oranje knop om een stap terug te gaan. Om te stoppen moet je linksboven op het toetsenbord op de Esc-knop drukken. 1 4 7

1 Net als bij enkelvoudige interest is bij samengestelde interest (afgekort SI) de hoogte van het interestbedrag afhankelijk van: Ø het bedrag dat ter beschikking wordt gesteld (= het kapitaal) Ø het interestpercentage Ø de tijdsduur dat het kapitaal ter beschikking wordt gesteld Zodra het interestbedrag berekend is, wordt dit bij samengestelde interest vanzelf aan het kapitaal toegevoegd en krijg je dus ook “rente over rente”. Daarom loopt de eindwaarde (= bedrag plus interest) bij samengestelde interest sneller op dan bij enkelvoudige interest, waarbij alleen over het oorspronkelijke kapitaal interest berekend wordt. Klik op de gele terug wilt naar de homeknop als je inhoudsopgave.

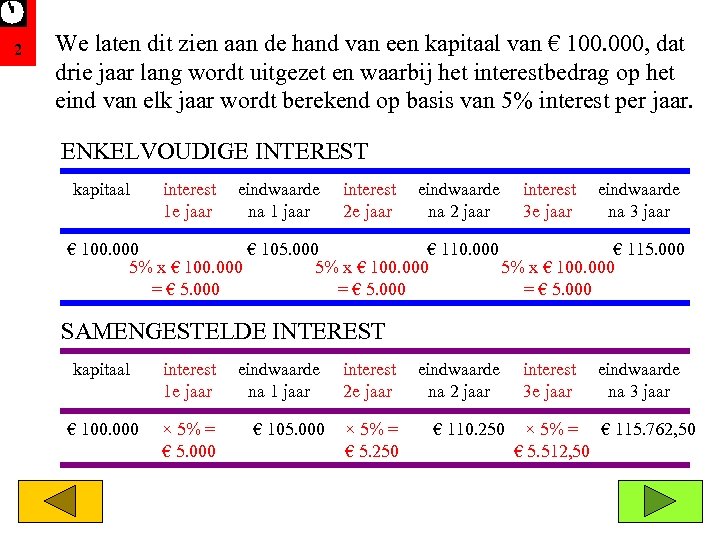2 We laten dit zien aan de hand van een kapitaal van € 100. 000, dat drie jaar lang wordt uitgezet en waarbij het interestbedrag op het eind van elk jaar wordt berekend op basis van 5% interest per jaar. ENKELVOUDIGE INTEREST kapitaal interest 1 e jaar eindwaarde na 1 jaar interest 2 e jaar eindwaarde na 2 jaar interest 3 e jaar eindwaarde na 3 jaar € 100. 000 € 105. 000 € 110. 000 € 115. 000 5% x € 100. 000 = € 5. 000 SAMENGESTELDE INTEREST kapitaal interest 1 e jaar eindwaarde na 1 jaar interest 2 e jaar eindwaarde na 2 jaar € 100. 000 × 5% = € 5. 000 € 105. 000 × 5% = € 5. 250 € 110. 250 interest 3 e jaar eindwaarde na 3 jaar × 5% = € 115. 762, 50 € 5. 512, 50

3 Zoals je ziet is er bij enkelvoudige interest sprake van maar één beginwaarde: het oorspronkelijke kapitaal. Alleen over dit bedrag wordt interest vergoed. In de praktijk komt dit alleen voor als het interestbedrag iedere keer direct wordt uitgekeerd of als de interest pas op het eind in één keer wordt berekend. Bij samengestelde interest kun je bij elke periode spreken van een nieuwe beginwaarde. Maar in zijn algemeenheid bedoelen we met de beginwaarde toch steeds het oorspronkelijke kapitaal. Een ander verschil is, dat bij enkelvoudige interest het interestpercentage normaal gesproken altijd per jaar luidt. Is dat niet het geval dan kun je het enkelvoudige interestpercentage gemakkelijk omrekenen naar een interestpercentage per jaar. Bij samengestelde interest kan het interestpercentage in allerlei perioden zijn uitgedrukt en kun je niet zo gemakkelijk het interestpercentage omrekenen naar een interestpercentage per jaar.

4 Hoe je bij samengestelde interest het ene interestpercentage kunt omrekenen naar een ander, zogenaamd “overeenkomstig interestpercentage”, zal nog aan bod komen. We gaan er in het navolgende steeds van uit dat bij samengestelde interest de (oorspronkelijke) beginwaarde alleen door bijschrijving van de interest verandert. In de voorbeelden zal gewerkt worden met geld dat gespaard wordt. Degene die het geld in ontvangst neemt, kun je als lener van dit geld beschouwen. Tussen de beginwaarde en elke willekeurige eindwaarde bestaat bij samengestelde interest een samenhang die is vastgelegd in de zogenaamde interestfactor (of oprentingsfactor): het getal waarmee je de beginwaarde moet vermenigvuldigen om de eindwaarde te krijgen.

5 Met behulp van de interestfactor gaat het berekenen van de eindwaarde een stuk sneller dan wanneer je telkens het interestbedrag bij de vorige eindwaarde moet optellen. Eens kijken of je al weet hoe je deze interestfactor kunt berekenen. Je zet voor drie jaar € 2. 000 weg tegen 1% samengestelde interest per maand. Met welk getal moet je € 2. 000 vermenigvuldigen om de eindwaarde te krijgen? A. 1, 36 C. 1, 4307. . B. 1, 4049. . D. Ik wil eerst meer uitleg. Klik op het goede antwoord.

Je zet voor drie jaar € 2. 000 weg tegen 1% samengestelde interest per maand. Met welk getal moet je € 2. 000 vermenigvuldigen om de eindwaarde te krijgen? A. 1, 36 B. 1, 4049. . C. 1, 4307. . D. Nog eens de uitleg.

Fout! Je bent uitgegaan van enkelvoudige interest. Klik op de knop. Je krijgt dan uitgelegd hoe het wel moet.

Fout! Bij samengestelde interest mag je 1% per maand niet gelijk stellen aan 12% per jaar. Je ziet dan de maandelijkse interestbijschrijving over het hoofd. Klik op de knop. Je krijgt dan uitgelegd hoe het wel moet.

De vraag is met welk getal je € 2. 000 moet vermenigvuldigen om bij 1% SI per maand de eindwaarde na drie jaar te krijgen. Op de volgende tijdbalk is een beginkapitaal van € 100. 000 ingetekend. Kijk eens goed hoe de eindwaarde van elke periode tot stand komt bij een looptijd van drie jaar en 5% SI per jaar. periode 1 periode 2 100. 000 Klik hier. periode 3

De vraag is met welk getal je € 2. 000 moet vermenigvuldigen om bij 1% SI per maand de eindwaarde na drie jaar te krijgen. Op de volgende tijdbalk is een beginkapitaal van € 100. 000 ingetekend. Kijk eens goed hoe de eindwaarde van elke periode tot stand komt bij een looptijd van drie jaar en 5% SI per jaar. periode 1 100. 000 periode 2 periode 3 + 5% = 105. 000 110. 250 x 1, 051 110. 250 x 1, 052 (= x 1, 1025) x 1, 053 (= x 1, 157625) 115. 762, 50 Zoals je ziet komt het aantal perioden dat tussen de begin- en eindwaarde zit, terug in de macht van de interestfactor. Gebruik je “i” voor het interestperunage en “n” voor het aantal perioden tussen begin- en eindwaarde, dan luidt de algemene formule voor de interestfactor: (1 + i)n. Klik op het plaatje als je meer wilt weten over machtsrekenen. Klik op de blauwe knop om het nog eens te proberen.

6 Goed De interestfactor waarmee je bij samengestelde interest een bedrag moet vermenigvuldigen om de eindwaarde van dit bedrag te krijgen, kun je berekenen als (1 + i)n, waarbij “n” staat voor het aantal interestperioden. Klik op de groene knop om door te gaan.

7 Om de eindwaarde van eenmalig bedrag bij samengestelde interest te berekenen, kun je gebruik maken van de formule: EWn = K × (1 + i)n Hierin staat “EW” voor de eindwaarde, “n” voor het aantal interestperioden tussen begin- en eindwaarde, “K” voor de beginwaarde en “i” voor het interestperunage (en “EWn” voor de eindwaarde na “n” perioden). Bij de TI-83 kun je gebruik maken van de functie “TVM Solver“ (TVM = Time Value Money) onder “Finance” om de eindwaarde te berekenen. Wil je aan de hand van een voorbeeld zien hoe deze functie werkt, klik dan op het plaatje van de TI-83.

Hiernaast zie je een afbeelding van de TI-83. We laten nu stap voor stap zien hoe je de functie TVM Solver in werking stelt. Klik op de groene knop.

Druk op de (gele) 2 nd-knop en dan op de x-1 -knop om het menu Finance op te roepen. (Klik er ook daadwerkelijk op om de volgende stap te zien. Dat geldt ook voor het vervolg. ) N. B. Heb je een TI-83 plus dan moet je eerst op de blauwe APPS-knop drukken. Je ziet dan Finance als eerste optie aangegeven. Door op ENTER te drukken activeer je deze functie. Het vervolg is hetzelfde als bij de gewone TI-83. Volg daarom gewoon de instructie voor de TI-83.

Zoals je ziet kun je bij het menu Finance kiezen voor “CALC” (= calculation) of “VARS” (variables). Het submenu dat je ziet, hoort bij de optie “CALC”. Zoals je ziet staat de TVM Solver als eerste functie in het rijtje. Druk nu op ENTER om deze functie te activeren. Opmerking: De TI-83 staat standaard op de eerste keuzemogelijkheid ingesteld. Wil je een van de andere opties hebben, dan moet je daar met de pijltjestoetsen naar toe gaan. CALC VARS 1: TVM Solver 2: tvm_Pmt 3: tvm_I% 4: tvm_PV 5: tvm_N 6: tvm_FV 7 npv(

De functie is nu geactiveerd. In principe staat de vorige invoer nog op het scherm. De “N” staat voor perioden, “I%” voor het interestpercentage, “PV” (= Present Value) voor de beginwaarde en “FV” (= Future Value) voor de eindwaarde. “PMT” (= Pay. Men. T of termijnbedrag) moet standaard op 0 staan. “P/Y” (= Payment/Year) en “C/Y” (= Calculation/Year) moeten beide op 1 staan. Van “PMT: END BEGIN” hoef je je bij samengestelde interest niets aan te trekken. Klik op de groene knop. N= I%= PV= PMT= FV= P/Y= C/Y= PMT: END BEGIN

Om bijvoorbeeld de eindwaarde van een kapitaal van € 200 dat acht perioden staat tegen 5% interest periode uit te rekenen, moet je met behulp van de pijltjestoetsen bij N 8 invullen, bij I% 5 (zonder procentteken) en bij PV 200 (en PMT op 0 en P/Y en C/Y op 1 stellen). Zoals je ziet is dat hier al gebeurd. Vervolgens moet je met behulp van de pijltjestoetsen op FV gaan staan. Druk nu op de (groene) ALPHA-knop en dan op ENTER (= SOLVE). Opmerking. Als er decimalen staan en je vindt dat storend, dan moet je op de MODE-knop drukken, met de pijltjestoets op “Float” gaan staan en op ENTER drukken. Vervolgens kun je via 2 nd-MODE (= “QUIT”) dit scherm afsluiten. De volgende keer dat je de functie “TVM Solver” gebruikt zullen er geen decimalen meer staan. N= 8 I%= 5 PV= 200 PMT= 0 FV= P/Y= 1 C/Y= 1 PMT: END BEGIN

Zoals je ziet, krijg je als eindwaarde – 295, 49 uit. Die – staat daar omdat je bij PV (+) 200 hebt ingevuld. De GRM beschouwt de PV als geleend bedrag en de FV als terugbetaling. De – geeft aan dat je dit bedrag kwijt bent. Wil je een positieve uitkomst, dan moet je bij PV – 200 invullen, waarbij je de (–) toets moet gebruiken om de min aan te geven. Je kunt de functie verlaten via 2 nd – MODE (= QUIT). Klik op de groene knop. N= 8 I%= 5 PV= 200 PMT= 0 FV= -295, 49 P/Y= 1 C/Y= 1 PMT: END BEGIN

8 Omdat bij samengestelde interest met eenmalige storting zonder tussentijdse opname de eindwaarde alleen aangroeit door interestbijschrijving, kun je het interestbedrag dat in een bepaalde periode ontvangen is, berekenen door simpelweg de waarde aan het begin af te trekken van de waarde aan het eind van de betreffende periode. Eens kijken of je dat lukt. Een kapitaal van € 5. 000 wordt tegen 2% SI per halfjaar weggezet. De vraag is hoe groot het interestbedrag in het vierde en vijfde jaar samen is. A. € 464, 16 C. € 214, 36 B. € 458, 99 D. Ik wil eerst meer uitleg.

Een kapitaal van € 5. 000 wordt tegen 2% SI per halfjaar weggezet. De vraag is hoe groot het interestbedrag in het vierde en vijfde jaar samen is. A. € 464, 16 B. € 458, 99 C. € 214, 36 D. Nog eens de uitleg.

Fout! Bij enkelvoudige interest mag je 2% per halfjaar gelijk stellen aan 4% per jaar. Bij samengestelde interest mag dat niet. Je mist dan per jaar één keer rente over rente. Klik op de knop. Je krijgt dan uitgelegd hoe het wel moet.

Fout! Je hebt niet gezien dat het om interest per half jaar ging en niet om interest per jaar. Klik op de knop. Je krijgt dan uitgelegd hoe het wel moet.

De vraag is hoe groot het interestbedrag in het vierde en vijfde jaar samen is als € 5. 000 tegen 2% SI per halfjaar wordt weggezet. Stel dat je een kapitaal van € 8. 000 tegen 1, 5% samengestelde interest per kwartaal wegzet en gevraagd wordt hoe groot het interestbedrag in het tweede jaar is. De waarde aan het begin van het tweede jaar is gelijk aan de eindwaarde van het eerste jaar. Omdat de interest per kwartaal is, is dat de eindwaarde na vier perioden. Die is € 8. 000 × 1, 0154 = € 8. 490, 91 (of via N = 4, I% = 1, 5 en PV = 8000 de FV zoeken). De waarde aan het eind van het tweede jaar is de eindwaarde na acht perioden. Die is € 8. 000 × 1, 0158 = € 9. 011, 94 (of via N = 8, I% = 1, 5 en PV = 8000 de FV zoeken). Het gevraagde bedrag is dus € 9. 011, 94 - € 8. 490, 91 = € 521, 03.

9 Klik op de groene knop om door te gaan.

10 De looptijd wordt vaak met behulp van datums aangegeven. Omdat bij samengestelde interest eigenlijk uitsluitend met hele perioden wordt gewerkt en het jaar steeds op 360 dagen wordt gesteld (dus een maand op dertig dagen; maar een week blijft zeven dagen), is het vrij eenvoudig om de looptijd met behulp van een tijdbalk te bepalen. Daarbij moet je wel zorgvuldig te werk gaan en er goed op letten dat je perioden telt en niet tijdstippen.

11 Eens kijken hoe “tijdbalkvaardig” je al bent. Je stort op 31 -3 -2004 eenmalig een bedrag tegen 1% SI per maand. Je wilt de eindwaarde op 1 -6 -2008 weten. Bij welke tijdbalk is deze begindatum goed aangegeven en klopt het aantal perioden? De blauwe pijl geeft de looptijd aan. A. 1 -1 -2004 1 -1 -2005 1 -1 -2006 1 -1 -2007 1 -1 -2008 1 -1 -2004 B. D. 1 -1 -2005 1 -1 -2006 1 -1 -2007 1 -1 -2008 50 perioden x 1 -1 -2004 C. 49 perioden x x 1 -1 -2004 x 1 -1 -2005 1 -1 -2006 1 -1 -2007 1 -1 -2008 50 perioden 1 -1 -2005 1 -1 -2006 1 -1 -2007 1 -1 -2008 51 perioden

Je stort op 31 -3 -2004 eenmalig een bedrag tegen 1% SI per maand. Je wilt de eindwaarde op 1 -6 -2008 weten. Bij welke tijdbalk is deze begindatum goed aangegeven en klopt het aantal perioden? De blauwe pijl geeft de looptijd aan. A. 1 -1 -2004 1 -1 -2005 1 -1 -2006 1 -1 -2007 1 -1 -2008 1 -1 -2004 B. D. 1 -1 -2005 1 -1 -2006 1 -1 -2007 1 -1 -2008 50 perioden x 1 -1 -2004 C. 49 perioden x x 1 -1 -2004 x 1 -1 -2005 1 -1 -2006 1 -1 -2007 1 -1 -2008 50 perioden 1 -1 -2005 1 -1 -2006 1 -1 -2007 1 -1 -2008 51 perioden

Fout! Je hebt tijdstippen geteld (de dwarsstreepjes) in plaats van perioden (de lijnstukjes tussen twee dwarsstreepjes). Klik op de knop om het opnieuw te proberen.

Fout! De begindatum is verkeerd ingetekend. Lees voor 31 -3 maar eens 1 -4. Klik op de knop om het opnieuw te proberen.

Fout! Je hebt tijdstippen geteld (de dwarsstreepjes) in plaats van perioden (de lijnstukjes tussen twee dwarsstreepjes) en de begindatum verkeerd ingetekend. Lees voor 31 -3 maar eens 1 -4. Klik op de knop om het opnieuw te proberen.

12 Goed Klik op de groene knop om door te gaan.

13 Je kunt ook de begindatum van de einddatum aftrekken. Omdat elke maand op 30 dagen is gesteld, moet je voor de 31 ste van de maand altijd de 30 ste nemen. Is het van(af) 28 februari (of in een schrikkeljaar 29 februari), dan moet je daar vanaf 30 februari van maken (want februari is ten einde). Wordt uitsluitend gebruik gemaakt van datums op het eind van de maand, dan is het echter veel handiger om alles gewoon één dag op te schuiven en voor de laatste van de maand dus de eerste van de volgende maand te gebruiken. Wil je zien hoe je op deze manier het aantal perioden kunt berekenen, klik dan op het plaatje hiernaast.

Stel dat je op 31 -5 -2000 een bepaald bedrag heb gestort tegen een bepaald samengesteld interestpercentage per maand en dat op de laatste van elke maand interest wordt bijgeschreven. Op 28 -2 -2005 wil je weten over hoeveel perioden je recht hebt gehad op interest. Links staat de berekening als je voor de 30 ste van de maand kiest en rechts als je voor de eerste van de volgende maand kiest. tot van (+ 12 =) 14 wi 2004 30 2 2005 30 5 2000 9 maanden 4 jaren (+12 =) 15 wi 2004 tot van 1 1 - 3 2005 6 2000 9 maanden 4 jaren Bij beide kom je uit op 57 maanden (= 9 + 4 x 12). Als je links 28 februari had laten staan, had je de twee ontbrekende dagen er zelf bij mogen tellen, omdat op 28 februari de interest over de hele voorafgaande periode wordt bijgeschreven.

14 Eens kijken of in staat bent de eindwaarde van een bedrag te berekenen als de looptijd met behulp van datums wordt gegeven. Hoeveel bedraagt de eindwaarde van een bedrag van € 500 dat van 1 -10 -2001 tot en met 30 -4 -2005 tegen 0, 25% SI per maand heeft uitgestaan? A. € 553, 75 B. € 555, 28 C. € 556, 67 D. Ik wil eerst meer uitleg.

Hoeveel bedraagt de eindwaarde van een bedrag van € 500 dat van 1 -10 -2001 tot en met 30 -4 -2005 tegen 0, 25% SI per maand heeft uitgestaan? A. € 553, 75 B. € 555, 28 C. € 556, 67 D. Nog eens de uitleg.

Fout! Je hebt met enkelvoudige interest gerekend. Klik op de knop. Je krijgt dan uitgelegd hoe het wel moet.

Fout! Je hebt een maand te weinig gerekend. Omdat het tot en met is, telt april 2005 helemaal mee. Klik op de knop. Je krijgt dan uitgelegd hoe het wel moet.

De vraag is hoeveel de eindwaarde bedraagt als je van 1 -10 -2001 tot en met 30 -4 -2005 € 500 tegen 0, 25% SI per maand wegzet. Stel dat je op 1 -8 -1999 € 2. 000 stort tegen 0, 4% samengestelde interest per maand en dat de interest op het eind van de maand wordt bijgeschreven. Op 31 -5 -2002 wil je na bijschrijving van de interest hele tegoed opnemen. Hoeveel bedraagt je tegoed als het bij deze ene storting gebleven is? Zet je de datums onder elkaar (waarbij je tot en met 31 -5 -2002 veranderd hebt in tot 1 -6 -2002), dan krijg je dit: van tot van 1 1 (+12 =) 18 6 8 - wi 2001 2002 1999 10 maanden 2 jaren Zo kom je op 10 + 2 × 12 = 34 perioden. De eindwaarde is dus € 2. 000 × 1, 00434 = € 2. 290, 74.

Je kunt natuurlijk ook weer gebruik maken van een tijdbalk. Hieronder is de tijdbalk in jaren al getekend. 1 -1 -1999 1 -8 -1999 1 -1 -2000 1 -1 -2001 1 -1 -2002 31 -5 -2002 1 -1 -2003 Om de begin- en eindtijd aan te geven moeten de maanden nog worden ingetekend. Hier gebeurt dat bij alle jaren. Zoals je bij de vorige vraag hebt gezien, hoeft dat voor de tussenliggende jaren eigenlijk niet. De looptijd wordt weer aangegeven met behulp van een pijl. Omdat het interestpercentage per maand is gegeven, moet je om het aantal perioden te weten, de maanden tellen: 5 (in 1999) + 12 (in 2000) + 12 (in 2001) + 5 (in 2002) = 34. Zo kom je dus ook op een eindwaarde van € 2. 000 × 1, 00434 = € 2. 290, 74.

15 Goed Denk er aan altijd van … tot … te nemen en bij een tijdbalk geen tijdstippen maar perioden te tellen. Klik op de groene knop om door te gaan.

16 Klik op het vliegtuigje om het berekenen van eindwaarden en interestbedragen met rente over rente te oefenen met open vragen. Omdat je de eindwaarde via een vermenigvuldiging uit een bepaalde beginwaarde kunt afleiden, kun je de beginwaarde via een deling uit de eindwaarde afleiden. We noemen deze beginwaarde de contante waarde. Met deze contante waarde kun je dezelfde berekeningen uitvoeren als met de eindwaarde. Gebruik je de TVM Solver op de TI-83, dan is nu de FV gegeven en moet je de PV uitrekenen.

17 Eens kijken of je al weet hoe je de contante waarde op 15 -10 -1998 kunt berekenen van een eindsaldo van € 173 dat op 157 -2002 na bijschrijving van de interest op een rekening staat. Er is nooit bijgestort of opgenomen en de interest is steeds 1, 5% SI per kwartaal geweest. A. 130 B. 138 C. 141 D. Ik wil eerst meer uitleg.

Hoeveel bedraagt de contante waarde op 15 -10 -1998 van een eindsaldo van € 173 dat op 15 -7 -2002 na bijschrijving van de interest op een rekening staat. Er nooit bijgestort of opgenomen en de interest is steeds 1, 5% SI per kwartaal geweest. Rond het bedrag af op hele euro’s. A. 130 B. 138 C. 141 D. Nog eens de uitleg.

Fout! Je kunt toch beter eerst eens naar de uitleg kijken. Klik op de knop.

Fout! Het is geen enkelvoudige interest. Klik op de knop. Je krijgt dan uitgelegd hoe het wel moet.

De vraag is hoeveel bij 1, 5% SI per kwartaal op 15 -10 -1998 de contante waarde bedraagt van € 173 die op 15 -7 -2002 na bijschrijving van de interest op een rekening staat. We laten het verband tussen eindwaarde en contante waarde zien aan de hand van een tijdbalk. We gaan uit van gegevens die al aan bod zijn gekomen bij de berekening van de eindwaarde. periode 1 100. 000 x 1, 051 periode 2 105. 000 x 1, 051 periode 3 110. 250 x 1, 051 Klik hier voor de contante waarde. 115. 762, 50

De vraag is hoeveel bij 1, 5 % SI per kwartaal op 15 -10 -1998 de contante waarde bedraagt van € 173 die op 15 -7 -2002 na bijschrijving van de interest op een rekening staat. We laten het verband tussen eindwaarde en contante waarde zien aan de hand van een tijdbalk. We gaan uit van gegevens die al aan bod zijn gekomen bij de berekening van de eindwaarde. periode 1 100. 000 x : 1, 051 1 1, 05 : periode 2 105. 000 1, 052 x : 1, 051 1 1, 05 periode 3 110. 250 (= : 1, 1025) : 1, 053 (= : 1, 157625) x : 1, 051 1 1, 05 115. 762, 50 Omdat delen door een bepaald getal hetzelfde oplevert als vermenigvuldigen met de inverse (= omgekeerde) van dat getal, kun je in plaats van € 105. 000 : 1, 051 ook € 105. 000 × nemen. is hetzelfde als 1, 05 -1, dus kun je de contante waarde ook als € 105. 000 × 1, 05 -1 uitrekenen.

Het mooie van de notatie 1, 05 -1 is dat de ‘-’ zo duidelijk aangeeft dat er bij de berekening van de contante waarde interest vanaf gaat. Voor de formule voor de contante waarde kun je dus kiezen uit CW = EW n , CW = EW × 1 n en CW = EW × (1 + i)-n. (1 + i) De berekening van de contante waarde van € 115. 762, 50 bij een looptijd van drie jaar tegen 5% SI per jaar is dus te berekenen als: 115. 762, 50 1 of 115. 762, 50 × 1, 05 -3 1, 053 Bij gebruik van de TVM Solver voer je in dat N = 3, I% = 5 en FV = 115762, 50 (en PMT = 0 en P/Y en C/Y = 1). Vervolgens ga je op PV staan en druk je op ALPHA en dan op ENTER.

18 Goed Klik op de groene knop om door te gaan.

19 Eens kijken of het volgende ook lukt. Van de telefoonmaatschappij krijg je bericht dat de rekening die je negen maanden geleden al had moeten betalen, is uitgegroeid tot een bedrag van € 259, 94. De telefoonmaatschappij rekent 0, 5% SI per week (!). Hoeveel euro interest heeft de telefoonmaatschappij in totaal berekend? A. € 45, 95 B. € 43, 10 C. € 42, 72 D. Ik wil eerst meer uitleg.

Van de telefoonmaatschappij krijg je bericht dat de rekening die je negen maanden geleden al had moeten betalen, is uitgegroeid tot een bedrag van € 259, 94. De telefoonmaatschappij rekent 0, 5% SI per week (!). Hoeveel euro interest heeft de telefoonmaatschappij in totaal berekend? A. € 45, 95 B. € 43, 10 C. € 42, 72 D. Nog eens de uitleg.

Fout! Het is toch beter dat je eerst even naar de uitleg kijkt. Klik op de knop.

Fout! Een maand is geen vier weken. Je mag wel twaalf maanden gelijk stellen aan 52 weken. Klik op de knop. Je krijgt dan uitgelegd hoe het wel moet.

De vraag is hoeveel euro interest de telefoonmaatschappij in totaal heeft berekend als een rekening in negen maanden is uitgegroeid tot een bedrag van € 259, 94 en de telefoonmaatschappij 0, 5% SI per week rekent. Het bedrag is alleen gegroeid door interest. Dat oorspronkelijke bedrag is de contante waarde van de gegeven eindwaarde. Omdat het interestpercentage in weken is gegeven, moet je om de contante waarde te vinden de negen maanden omzetten in weken. Daarbij moet je gebruik maken van de regel dat 1 jaar = 4 kwartalen = 12 maanden = 52 weken. Met behulp van een kruistabel kun je dit probleem als volgt weergeven: 12 maanden 52 weken 9 maanden ? weken Nu nog even kruislings vermenigvuldigen …

20 Goed Klik op de groene knop om door te gaan.

21 En nu nog een lastige. Op 1 -6 -2008 krijg je van je ouders € 1. 000 uitgekeerd als je tot die tijd niet gerookt hebt. Je ouders hebben voor dit doel op 1 -12 -2002 € 800 op de bank vastgezet tegen 1% SI per kwartaal. Hoeveel euro hebben je ouders te veel of te weinig gestort? A. € 36, 21 te veel B. € 27, 95 te veel C. € 4, 23 te weinig D. € 3, 40 te weinig

Op 1 -6 -2008 krijg je van je ouders € 1. 000 uitgekeerd als je tot die tijd niet gerookt hebt. Je ouders hebben voor dit doel op 1 -12 -2002 € 800 op de bank vastgezet tegen 1% SI per kwartaal. Hoeveel euro hebben je ouders te veel of te weinig gestort? A. € 36, 21 te veel B. € 27, 95 te veel C. € 4, 23 te weinig D. € 3, 40 te weinig

Fout! Je hebt de eindwaarde op 1 -6 -2008 berekend, terwijl je had moeten berekenen hoeveel op 1 -12 -2002 had moeten worden gestort. Bovendien heb je een jaar te weinig gerekend. Klik op de knop om het opnieuw te proberen.

Fout! Je hebt een jaar te weinig gerekend. Klik op de knop om het opnieuw te proberen.

Fout! Je hebt de eindwaarde op 1 -6 -2008 berekend, terwijl je had moeten berekenen hoeveel op 1 -12 -2002 had moeten worden gestort. Klik op de knop om het opnieuw te proberen.

22 Goed Klik op de groene knop om door te gaan.

23 Tot nu toe is steeds gewerkt met het berekenen van samengestelde interest over hele interestperioden. In principe kun je ook over delen van een interestperiode met samengestelde interest rekenen, maar in de praktijk wordt daarvoor meestal met enkelvoudige interest gerekend. Zou je over delen van een periode ook samengestelde interest rekenen, dan zie je dat bij samengestelde interest al vanaf het begin sprake is van een ander verloop van de eindwaarde dan bij enkelvoudige interest.

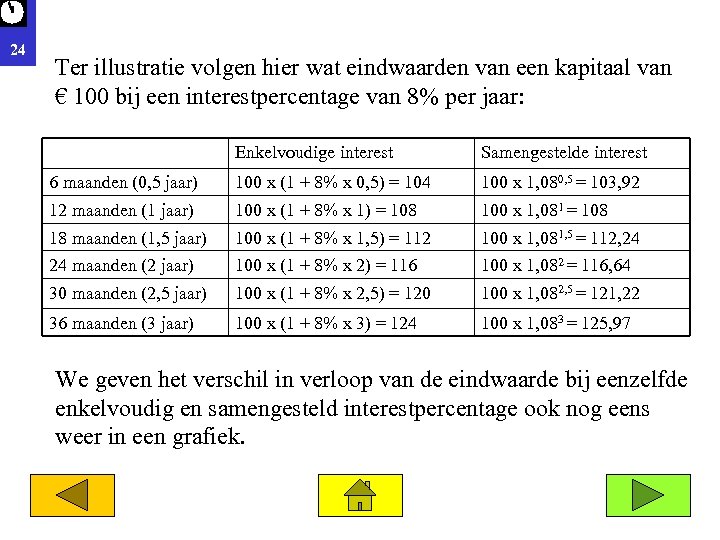24 Ter illustratie volgen hier wat eindwaarden van een kapitaal van € 100 bij een interestpercentage van 8% per jaar: Enkelvoudige interest Samengestelde interest 6 maanden (0, 5 jaar) 100 x (1 + 8% x 0, 5) = 104 100 x 1, 080, 5 = 103, 92 12 maanden (1 jaar) 100 x (1 + 8% x 1) = 108 100 x 1, 081 = 108 18 maanden (1, 5 jaar) 100 x (1 + 8% x 1, 5) = 112 100 x 1, 081, 5 = 112, 24 24 maanden (2 jaar) 100 x (1 + 8% x 2) = 116 100 x 1, 082 = 116, 64 30 maanden (2, 5 jaar) 100 x (1 + 8% x 2, 5) = 120 100 x 1, 082, 5 = 121, 22 36 maanden (3 jaar) 100 x (1 + 8% x 3) = 124 100 x 1, 083 = 125, 97 We geven het verschil in verloop van de eindwaarde bij eenzelfde enkelvoudig en samengesteld interestpercentage ook nog eens weer in een grafiek.

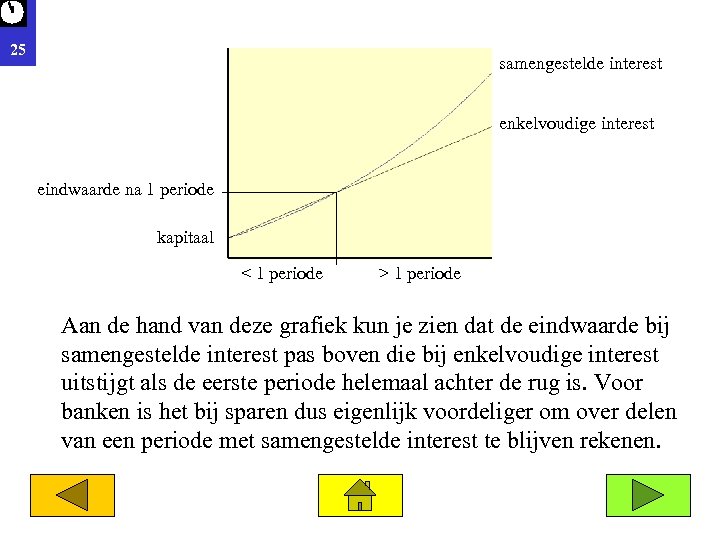25 samengestelde interest enkelvoudige interest eindwaarde na 1 periode kapitaal < 1 periode > 1 periode Aan de hand van deze grafiek kun je zien dat de eindwaarde bij samengestelde interest pas boven die bij enkelvoudige interest uitstijgt als de eerste periode helemaal achter de rug is. Voor banken is het bij sparen dus eigenlijk voordeliger om over delen van een periode met samengestelde interest te blijven rekenen.

26 Verder kun je uit het verschil in verloop van de eindwaarde afleiden dat je voor een enkelvoudig interestpercentage geen overeenkomstig samengesteld interestpercentage kunt vinden. Met zo’n overeenkomstig interestpercentage (ook wel gelijkwaardig interestpercentage genoemd) wordt een interestpercentage bedoeld dat steeds dezelfde eindwaarde oplevert. Dat houdt in dat als je de opbrengst van een spaarvorm of kosten van een lening op basis van enkelvoudige interest wilt vergelijken met die op basis van samengestelde interest, je altijd van een bepaalde looptijd moet uitgaan. Door vervolgens voor beide interestvormen de eindwaarde van een bepaald bedrag uit te rekenen, kun je gemakkelijk bepalen welke interestvorm bij die bepaalde looptijd het beste resultaat oplevert.

27 Eens kijken of je met de volgende variant uit de voeten kunt. Je overweegt om je spaargeld voor vier jaar vast te zetten. Op de site van een internetbank heb je gelezen dat deze bank je dan 0, 5% samengestelde interest per maand biedt. Een andere bank biedt een spaarvorm aan op basis van enkelvoudige interest. Hoeveel procent enkelvoudige interest moet deze bank je minimaal bieden om aantrekkelijk te zijn? Ga ervan uit dat beide interestpercentages voor vier jaar vaststaan. Rond het interestpercentage naar boven af op één cijfer achter de komma. A. 31, 8% per jaar C. 6, 8% per jaar B. 27, 1% per jaar D. Ik wil eerst meer uitleg.

Welk enkelvoudig interestpercentage levert bij een looptijd van vier jaar evenveel op als een samengesteld interestpercentage van 0, 5% per maand? Rond het interestpercentage naar boven af op één cijfer achter de komma. A. 31, 8% per jaar B. 27, 1% per jaar C. 6, 8% per jaar D. Nog eens de uitleg.

Fout! Je kunt toch beter eerst eens naar de uitleg kijken. Klik op de knop.

Fout! Dit is het enkelvoudige interestpercentage per vier jaar. Klik op de knop. Je krijgt dan uitgelegd hoe het wel moet.

De vraag is welk enkelvoudig interestpercentage bij een looptijd van vier jaar evenveel oplevert als 0, 5% samengestelde interest per maand. Het probleem is in eerste instantie dat er geen bedrag gegeven is. Dat kun je stellen. Bij procenten is het meestal het gemakkelijkste om te werken met € 100. Stel eens dat het samengestelde interestpercentage 1% per kwartaal was geweest en de looptijd drie jaar. € 100 groeit dan aan tot € 100 × 1, 0112 = € 112, 68. Dat is dus € 12, 68 interest in drie jaar tijd. Op basis van enkelvoudige interest betekent dat xxx € 12, 68 / 3 = € 4, 22 interest per jaar. Omdat het kapitaal € 100 is, is dat 4, 22% per jaar. Nu is het alleen nog even oppassen met afronden. Omdat € 112, 68 en € 4, 22 naar beneden zijn afgerond, is 4, 22% eigenlijk net iets te weinig.

28 Goed Klik op de groene knop om door te gaan.

29 Zijn de te vergelijken spaarvormen of leningen allemaal op basis van samengestelde interest en verschillen ze alleen in de definitie van de tijd (bijvoorbeeld de een in % per maand en de ander in % per kwartaal), dan kun je altijd een vergelijking maken op basis van een overeenkomstig interestpercentage. Zo komt een samengesteld interestpercentage van 5, 83% per half jaar bijna volledig overeen met een samengesteld interestpercentage van 12% per jaar. Met behulp van de TVM Solver is dat eenvoudig te controleren door uit te gaan van een kapitaal van € 100 en daarvan de eindwaarde na één jaar uit te rekenen tegen 12% per jaar. Vervolgens kijk je hoeveel perioden bij het te vinden overeenkomstige interestpercentage in één jaar gaan. Dat aantal vul je in bij “N”. De “PV” en de gevonden “FV” laat je gewoon staan en je rekent nu “I%” uit.

30 Eens kijken of je ook zelf een overeenkomstig interestpercentage kunt berekenen. Bij een bank kun je een lening afsluiten tegen 15% samengestelde interest per jaar. Hoeveel is het overeenkomstige samengestelde interestpercentage per maand (afgerond op twee decimalen)? A. 1, 01% B. 1, 17% C. 1, 25% D. Ik wil eerst meer uitleg.

Bij een bank kun je een lening afsluiten tegen 15% samengestelde interest per jaar. Hoeveel is het overeenkomstige samengestelde interestpercentage per maand (afgerond op twee decimalen)? A. 1, 01% B. 1, 17% C. 1, 25% D. Nog eens de uitleg.

Fout! Je kunt toch beter eerst eens naar de uitleg kijken. Klik op de knop.

Fout! Het is geen enkelvoudige interest. Klik op de knop. Je krijgt dan uitgelegd hoe het wel moet.

De vraag is hoeveel het overeenkomstige samengestelde interestpercentage per maand is van 15% samengestelde interest per jaar. Stel, je wilt weten welk percentage per maand overeenkomt met een percentage van 1% per kwartaal. Je vult bij de TVM Solver nu in “N” = 4, “I%” = 1 en “PV” = 100 (“PMT” laat je op 0 staan en “P/Y” en “C/Y” op 1) en je rekent “FV” uit. Dat blijkt – 104, 06 te zijn. Nu vul je voor “N” 12 in en reken je “I%” uit. Dat blijkt 0, 33% te zijn (afgerond op twee decimalen). Het kan ook zonder TVM Solver. In dat geval moet je beredeneren dat één maand gelijk is aan 1/3 kwartaal. Als je € 100 één maand laat staan, krijg je als eindwaarde € 100 × 1, 011/3 = € 100, 33 (afgerond). Een interestbedrag van € 0, 33 in één maand tijd bij een kapitaal van € 100 houdt in dat het interestpercentage 0, 33% per maand is.

31 Goed Klik op de groene knop om door te gaan.

32 Voordat je de gelegenheid krijgt om te oefenen met samengestelde interest, zetten we de belangrijkste regels nog eens op rij. Bij berekeningen met samengestelde interest kijken we alleen naar hele perioden. Je kunt: - de eindwaarde uitrekenen als EW = K × (1 + i)n (of als FV via de TVM Solver) en de contante waarde als CW = EW / (1 + i)n of EW × (1 + i)-n (of als PV via de TVM Solver). - het totale interestbedrag uitrekenen door de beginwaarde af te trekken van de eindwaarde. Bij beide berekeningen moeten i en n dezelfde tijdseenheid hebben, waarbij geldt: 1 jaar = 4 kwartalen = 12 maanden = 360 dagen = 52 weken (ook al is dit laatste niet geheel correct). Door de tijd te stellen op van … tot … kun je door de datums van elkaar af te trekken de looptijd vinden.

33 Met behulp van de eindwaarde na één jaar van een kapitaal van € 100 kun je uitvinden welk interestpercentage met een andere looptijd hetzelfde resultaat oplevert. Je hoeft de “N” maar aan te passen en de “I%” als onbekende te nemen. Klik op het vliegtuigje om het rekenen met samengestelde interest te oefenen met open vragen. Je bent nu aan het einde van de gewone onderwerpen gekomen. Wil je weten hoe je in Excel de eindwaarde of de contante waarde kunt berekenen, klik dan op de groene knop. Klik op de home-knop als je een eerder onderwerp wilt herhalen. Druk op de Esc-toets (linksboven op het toetsenbord) om af te sluiten.

Wiskundigen spreken van exponenten in plaats van machten. Je hebt al gezien dat 1, 051 × 1, 051 = 1, 052 en dat 1, 051 × 1, 051 = 1, 053. In de dagelijkse praktijk wordt de toevoeging “tot de macht 1” meestal weggelaten. Als je dezelfde (grond)getallen met elkaar vermenigvuldigt, hoef je de exponenten maar bij elkaar op te tellen. 1, 055 × 1, 052 is dus 1, 057 (= 1, 05 × 1, 05 × 1, 05). Is er sprake van een deling, dan moet je de exponenten van elkaar aftrekken. 1, 055 / 1, 052 is dus 1, 053. In plaats van te delen door 1, 052 had je ook kunnen vermenigvuldigen met. Dit kun je schrijven als 1, 05 -2. Dus 1, 055 / 1, 052 = 1, 055 × 1, 05 -2 = 1, 053.

De knop voor machtsverheffen is op de TI-83 aangegeven met een ^. Om bijvoorbeeld 1, 053 in te voeren, typ je eerst 1. 05, dan druk je op de ^ -knop, dan typ je 3 en vervolgens druk je op ENTER. Als de exponent negatief is, moet je, nadat je op de ^ -knop hebt gedrukt, de min intypen door op de (-) knop te drukken. Kijk nu eens of je 1, 06 -2 kunt invoeren. Je moet 0, 8899… uitkrijgen. Met behulp van de negatieve macht kun je ook gemakkelijk aantonen dat een getal tot de macht 0 altijd 1 is: 1 a 1 × a-1 = a 0 en a × a = = 1. a a De enige uitzondering is het getal 0. Net zo min als je mag delen door 0, mag je 00 gebruiken.

Worteltrekken is de inverse (= omgekeerde) bewerking van machtsverheffen: 32 = 9 en = 3. 1 a Omdat de inverse is van a, is afgesproken dat je worteltrekken kunt aangeven door het grondgetal te voorzien van een exponent in de vorm van 1 , dus = 9½. a Om op je rekenmachine de goede uitkomst te krijgen voor 9½ , moet je de breuk tussen haakjes zetten (want anders denkt de rekenmachine dat je 91 : 2 bedoelt). Je kunt natuurlijk ook 0, 5 in plaats van ½ gebruiken.

Door te combineren zijn zelfs de meest exotische vormen van een grondgetal te herleiden tot het grondgetal met maar één exponent. Zo is 1 hetzelfde als 9 -2/3 (want - = 1/. . en /3 = ). Onthoud goed dat je bij het vermenigvuldigen de exponenten bij elkaar mag optellen als het grondgetal hetzelfde is. Zo geldt dat 1, 065 × 1, 060, 7 × 1, 06 -3 = 1, 065+0, 7 -3 = 1, 062, 7 = 1, 17. . Klik op de blauwe knop om de opgave nog eens te proberen.

34 In Excel kun je de eindwaarde berekenen met behulp van de financiële functie TW (= Toekomstige Waarde) en de contante waarde met behulp van de functie HW (= Huidige Waarde). Beide functies zijn eigenlijk bedoeld om te rekenen met een zogenaamde “rente” (waarbij sprake is van periodieke betalingen). Daarom hoef je niet alle velden in te vullen. Omdat je bij beide functies op dezelfde manier te werk moet gaan, laten we aan de hand van een simulatie alleen zien hoe de functie TW werkt.

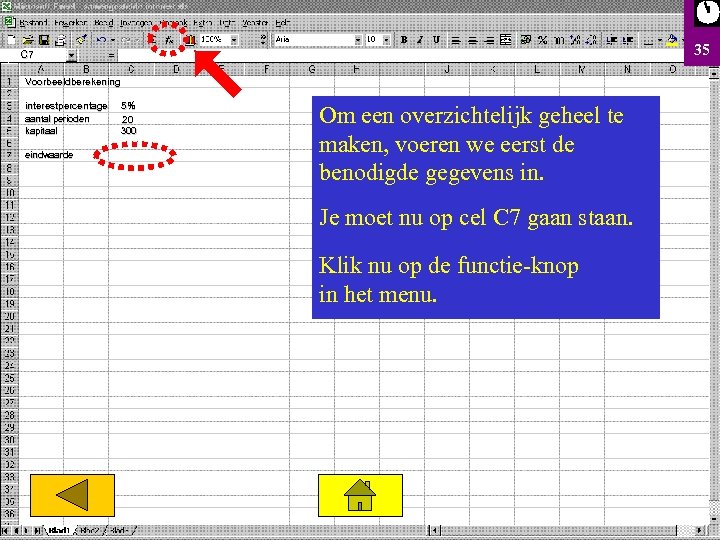35 . C 7 Voorbeeldberekening interestpercentage aantal perioden kapitaal eindwaarde 5% . 20 300 Om een overzichtelijk geheel te maken, voeren we eerst de benodigde gegevens in. Je moet nu op cel C 7 gaan staan. Klik nu op de functie-knop in het menu.

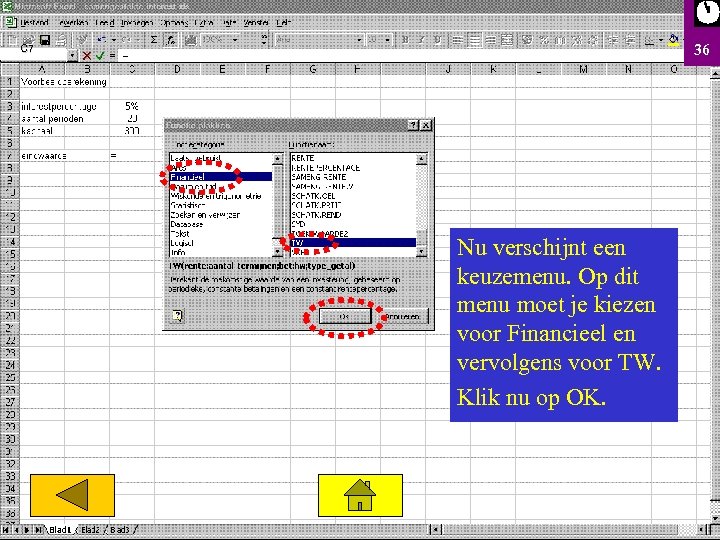36 . C 7 Nu verschijnt een keuzemenu. Op dit menu moet je kiezen voor Financieel en vervolgens voor TW. Klik nu op OK.

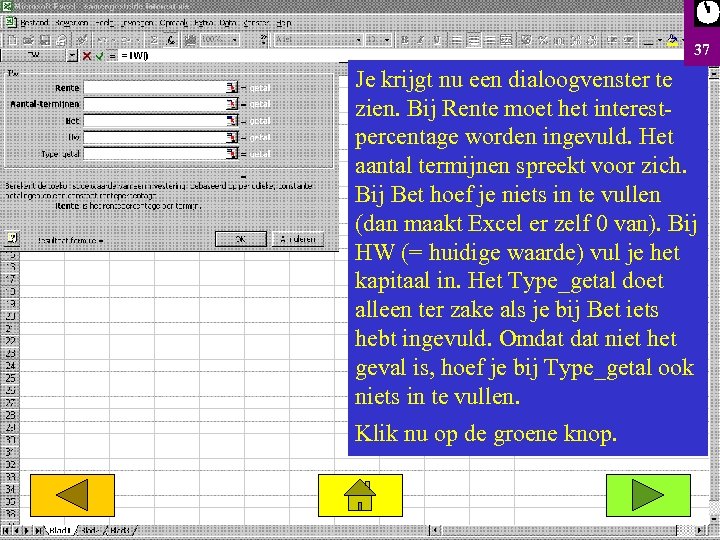37 Je krijgt nu een dialoogvenster te zien. Bij Rente moet het interestpercentage worden ingevuld. Het aantal termijnen spreekt voor zich. Bij Bet hoef je niets in te vullen (dan maakt Excel er zelf 0 van). Bij HW (= huidige waarde) vul je het kapitaal in. Het Type_getal doet alleen ter zake als je bij Bet iets hebt ingevuld. Omdat niet het geval is, hoef je bij Type_getal ook niets in te vullen. Klik nu op de groene knop.

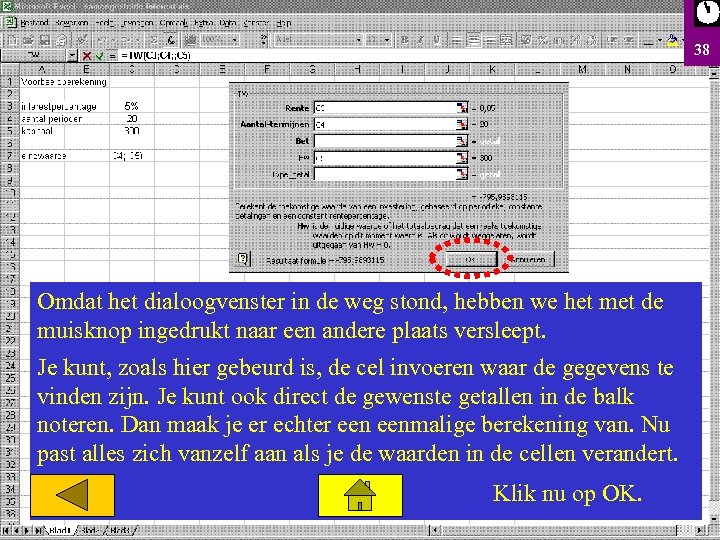38 Omdat het dialoogvenster in de weg stond, hebben we het met de muisknop ingedrukt naar een andere plaats versleept. Je kunt, zoals hier gebeurd is, de cel invoeren waar de gegevens te vinden zijn. Je kunt ook direct de gewenste getallen in de balk noteren. Dan maak je er echter eenmalige berekening van. Nu past alles zich vanzelf aan als je de waarden in de cellen verandert. Klik nu op OK.

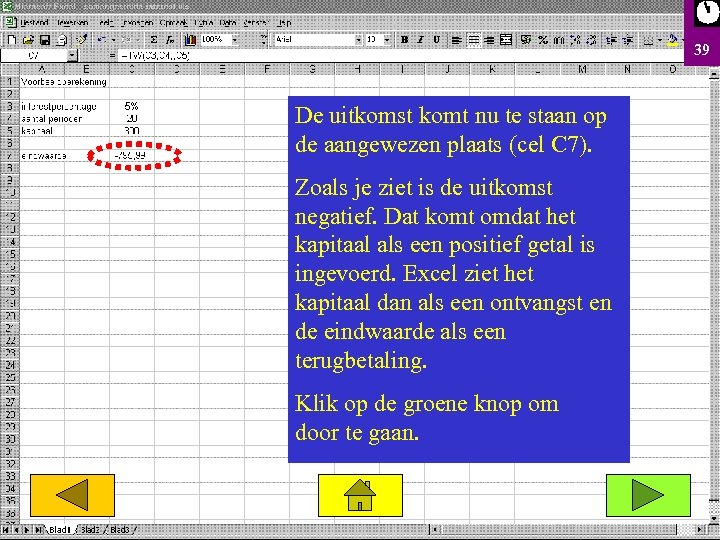39 De uitkomst komt nu te staan op de aangewezen plaats (cel C 7). Zoals je ziet is de uitkomst negatief. Dat komt omdat het kapitaal als een positief getal is ingevoerd. Excel ziet het kapitaal dan als een ontvangst en de eindwaarde als een terugbetaling. Klik op de groene knop om door te gaan.

40 Je kunt natuurlijk ook zelf de formule K × (1+i)n invoeren om de eindwaarde te berekenen met behulp van het kapitaal, het interestperunage en het aantal perioden. Voor de contante waarde kun je gebruik maken van de formule EW / (1+i)n. Je bent nu aan het definitieve einde van deze presentatie gekomen. Wil je oefenen met de functies TW en HW in Excel, klik dan op het uiltje. Klik op de home-knop als je een eerder onderwerp wilt herhalen. Druk op de Esc-toets (linksboven op het toetsenbord) om af te sluiten.