Welcome to our Maths Workshop for parents

Welcome to our Maths Workshop for parents – thank you so much for coming! There is a selection of maths resources arranged on the tables around the edge of the hall – please feel free to have parents and have a Welcome to our Maths Workshop fora look – thank you so much ‘play’! for coming! Using models and images in maths is essential in helping the children understand underlying patterns and principles of maths.

Learning, Growing and Succeeding Together

Oh no!!!

etc.

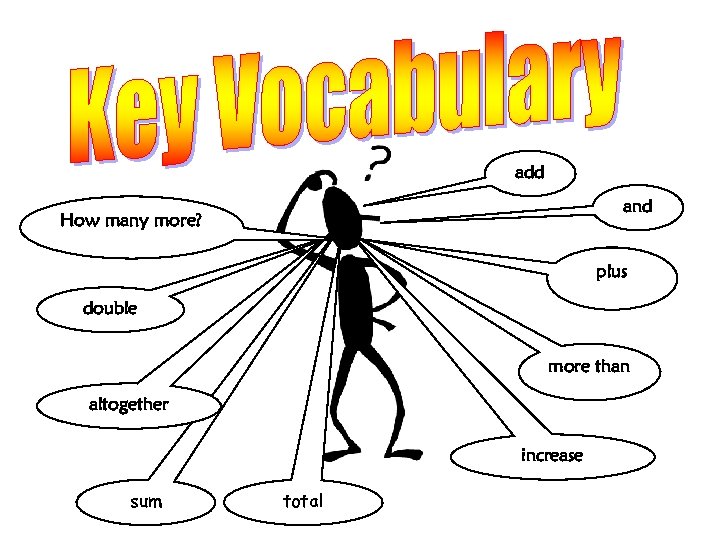add and How many more? plus double more than altogether increase sum total

The Downley Staff – and guests!

Mental Recall of Number Bonds … This is REALLY IMPORTANT!!!

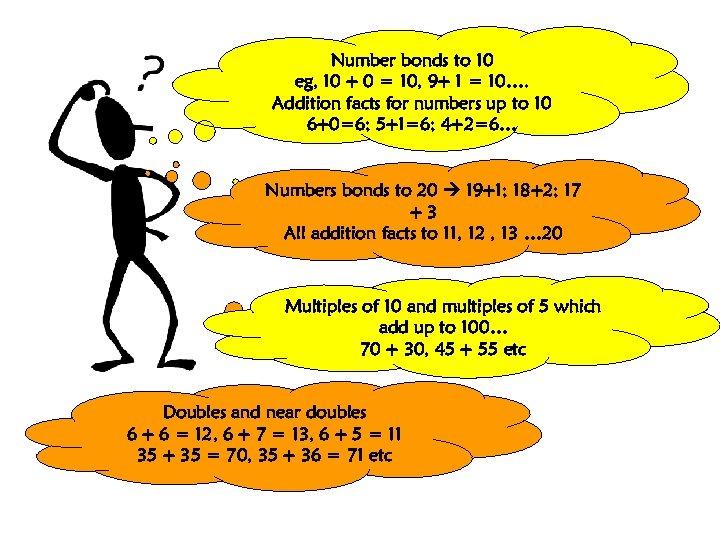Number bonds to 10 eg, 10 + 0 = 10, 9+ 1 = 10…. Addition facts for numbers up to 10 6+0=6; 5+1=6; 4+2=6… Numbers bonds to 20 19+1; 18+2; 17 +3 All addition facts to 11, 12 , 13 … 20 Multiples of 10 and multiples of 5 which add up to 100… 70 + 30, 45 + 55 etc Doubles and near doubles 6 + 6 = 12, 6 + 7 = 13, 6 + 5 = 11 35 + 35 = 70, 35 + 36 = 71 etc

‘Sums!!!’

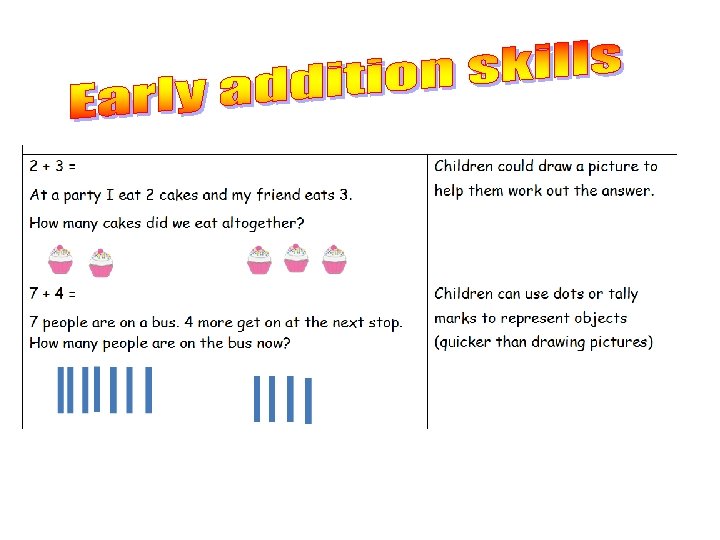
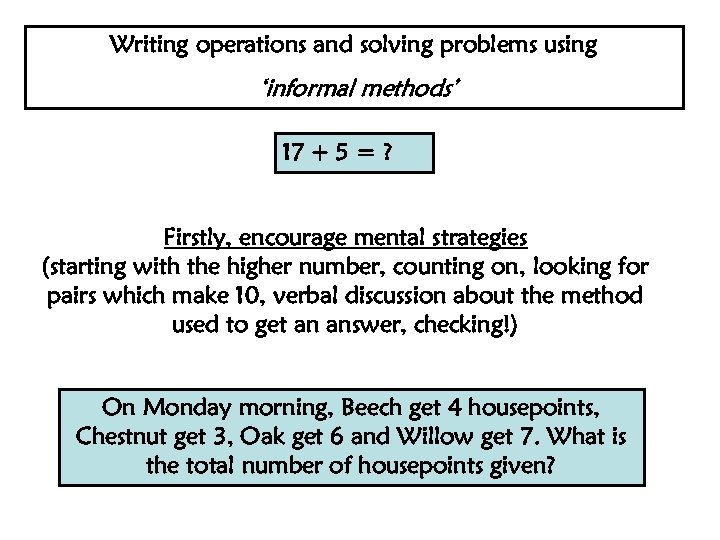Writing operations and solving problems using ‘informal methods’ 17 + 5 = ? Firstly, encourage mental strategies (starting with the higher number, counting on, looking for pairs which make 10, verbal discussion about the method used to get an answer, checking!) On Monday morning, Beech get 4 housepoints, Chestnut get 3, Oak get 6 and Willow get 7. What is the total number of housepoints given?

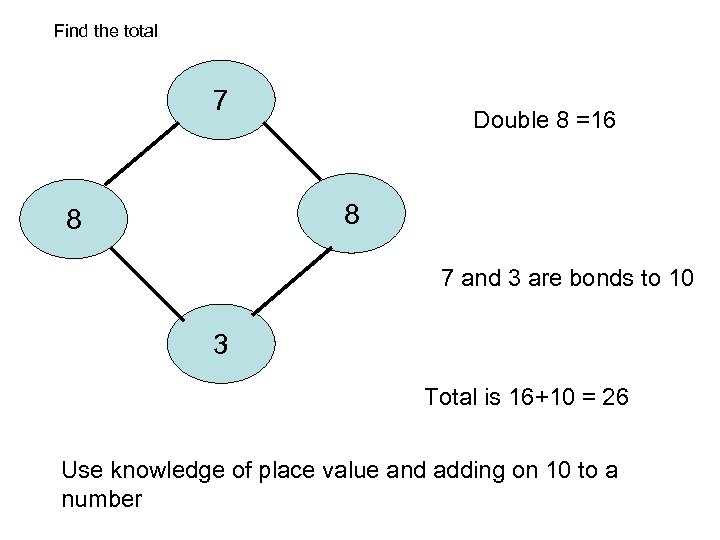Find the total 7 Double 8 =16 8 8 7 and 3 are bonds to 10 3 Total is 16+10 = 26 Use knowledge of place value and adding on 10 to a number

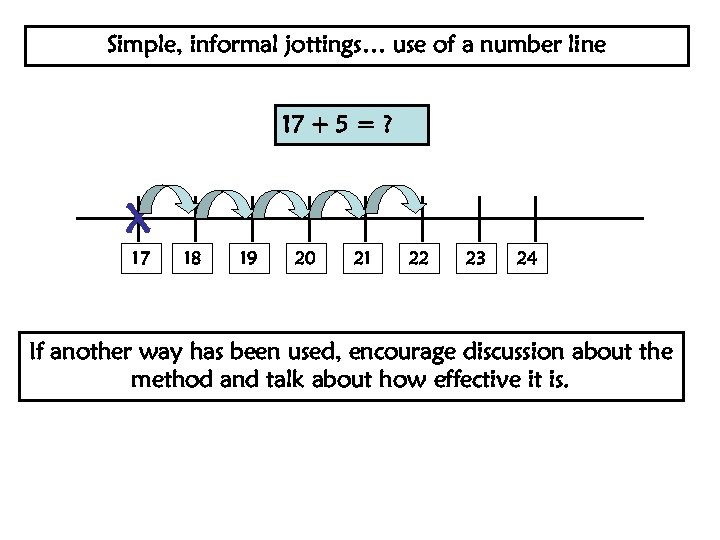Simple, informal jottings… use of a number line 17 + 5 = ? X 17 18 19 20 21 22 23 24 If another way has been used, encourage discussion about the method and talk about how effective it is.

The importance of understanding PLACE VALUE

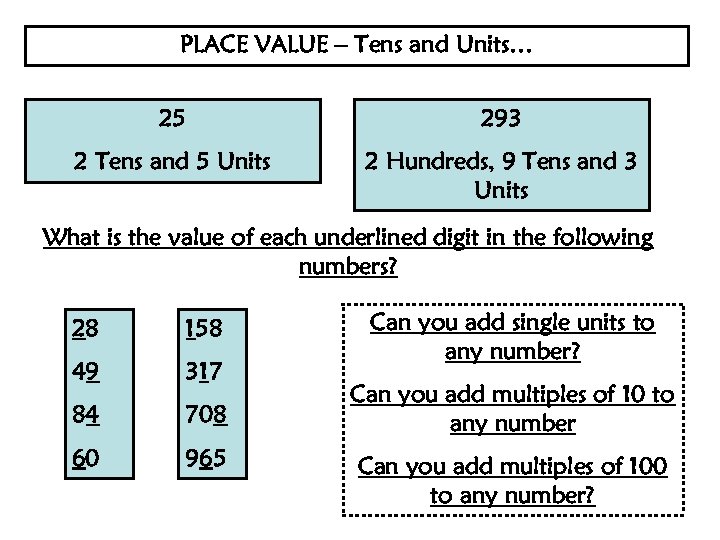PLACE VALUE – Tens and Units… 25 293 2 Tens and 5 Units 2 Hundreds, 9 Tens and 3 Units What is the value of each underlined digit in the following numbers? 28 158 49 317 84 708 60 965 Can you add single units to any number? Can you add multiples of 10 to any number Can you add multiples of 100 to any number?

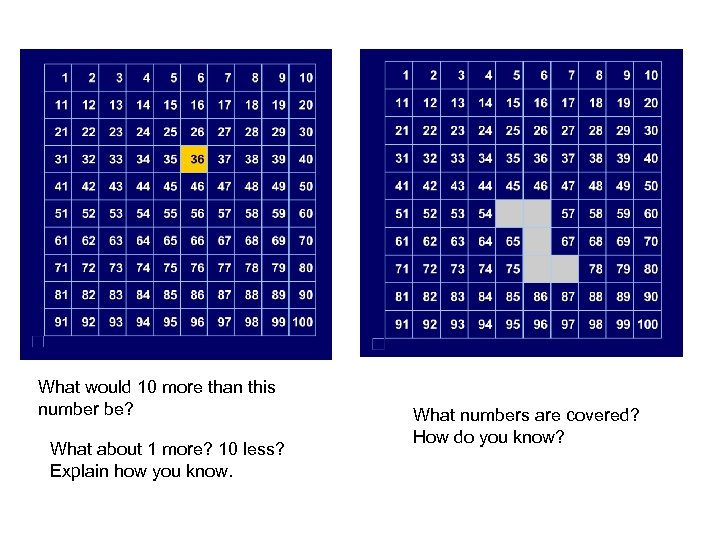What would 10 more than this number be? What about 1 more? 10 less? Explain how you know. What numbers are covered? How do you know?

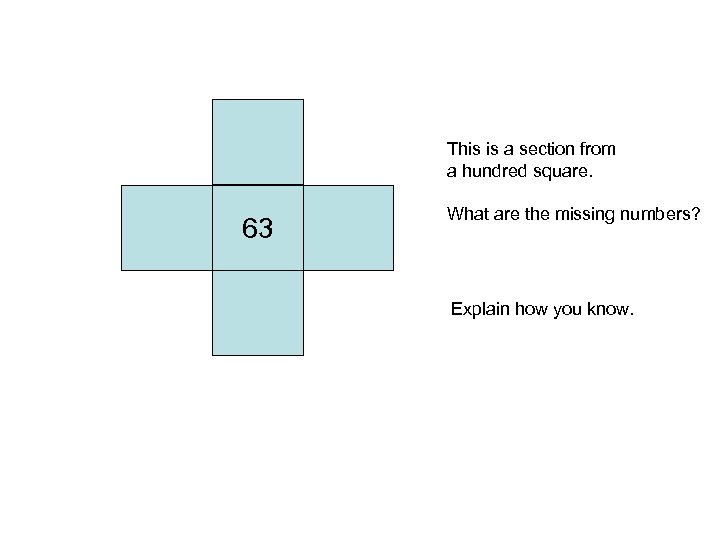This is a section from a hundred square. 63 What are the missing numbers? Explain how you know.

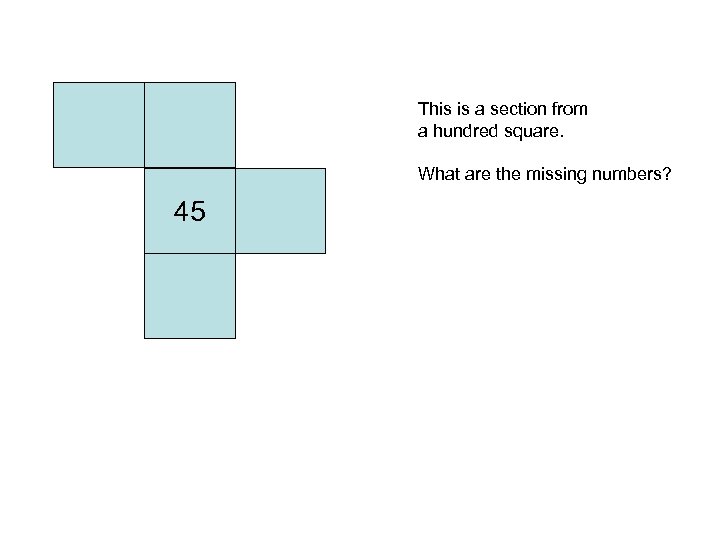This is a section from a hundred square. What are the missing numbers? 45

48 + 1 = 139 + 1 = 299 + 1 = 48 + 10 = 139 + 10 = 299 + 10 = 48 + 100 = 139 + 100 = 299 + 100 = 48 + 3 = 139 + 6 = 299 + 9 = 48 + 30 = 139 + 60 = 299 + 90 = 48 + 300 = 139 + 600 = 299 + 900 =

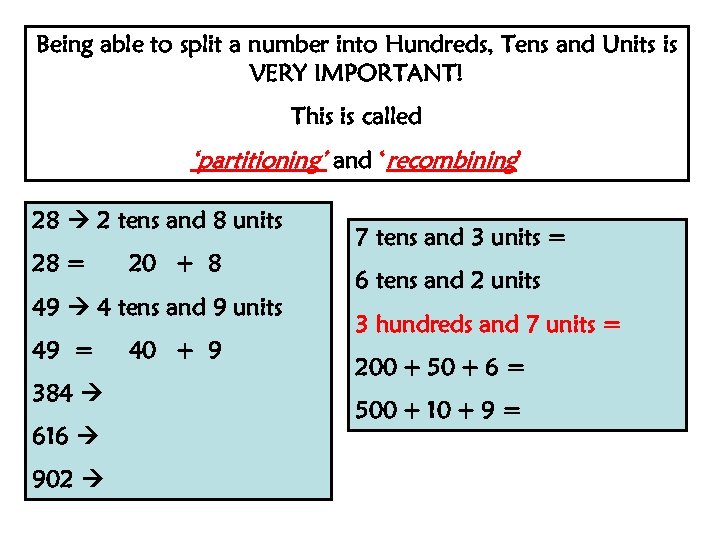Being able to split a number into Hundreds, Tens and Units is VERY IMPORTANT! This is called ‘partitioning’ and ‘recombining’ 28 2 tens and 8 units 28 = 20 + 8 49 4 tens and 9 units 49 = 384 616 902 40 + 9 7 tens and 3 units = 6 tens and 2 units 3 hundreds and 7 units = 200 + 50 + 6 = 500 + 10 + 9 =

Different ways of adding up – mentally and with jottings…

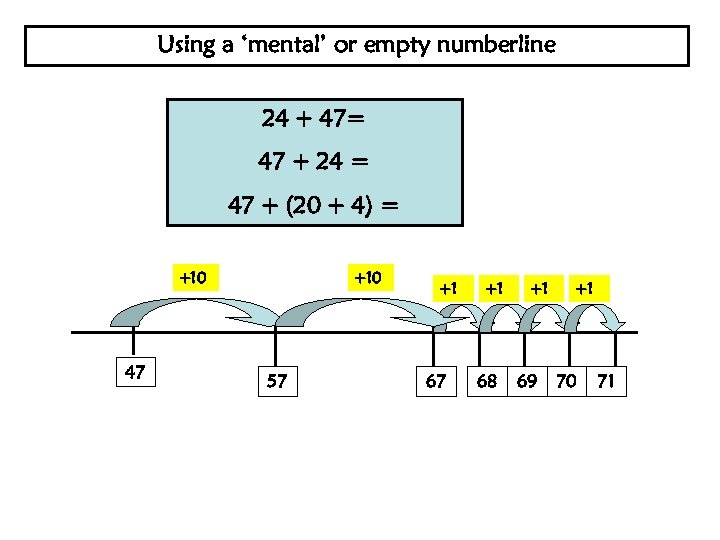Using a ‘mental’ or empty numberline 24 + 47= 47 + 24 = 47 + (20 + 4) = +10 +1 +1 X 47 57 67 68 69 70 71

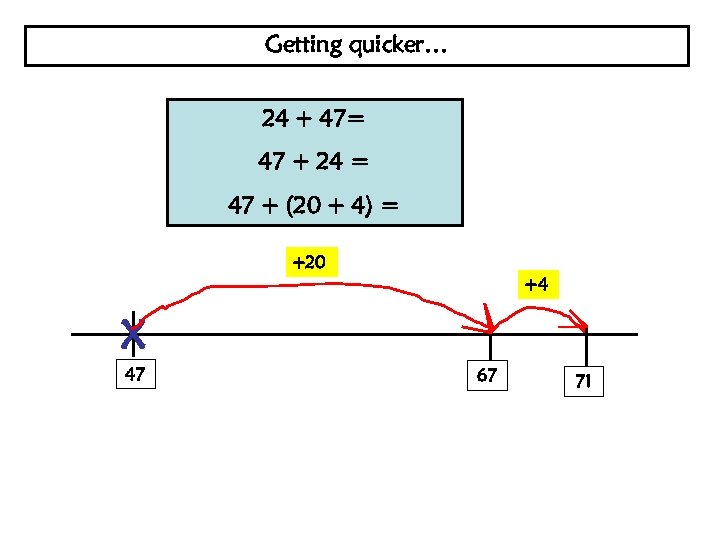Getting quicker… 24 + 47= 47 + 24 = 47 + (20 + 4) = +20 +4 X 47 67 71

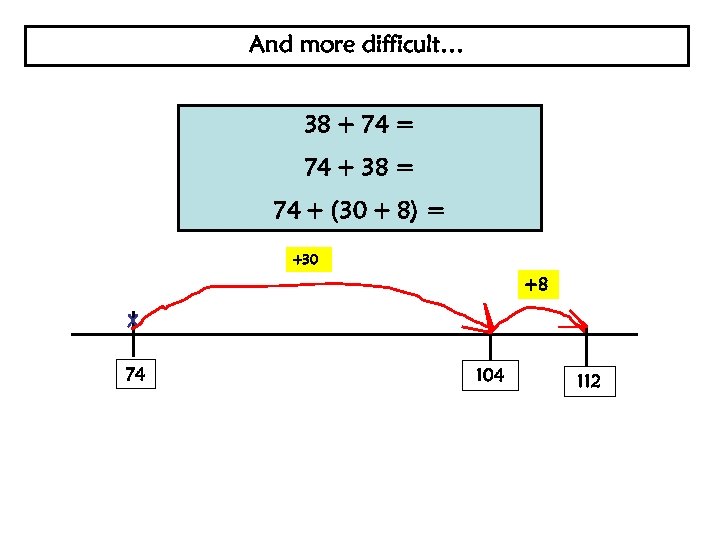And more difficult… 38 + 74 = 74 + 38 = 74 + (30 + 8) = +30 +8 X 74 104 112

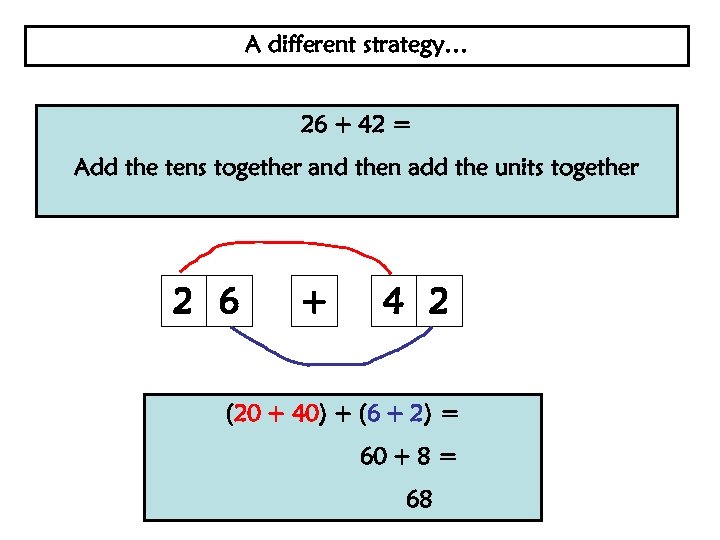A different strategy… 26 + 42 = Add the tens together and then add the units together 2 6 + 4 2 (20 + 40) + (6 + 2) = 60 + 8 = 68

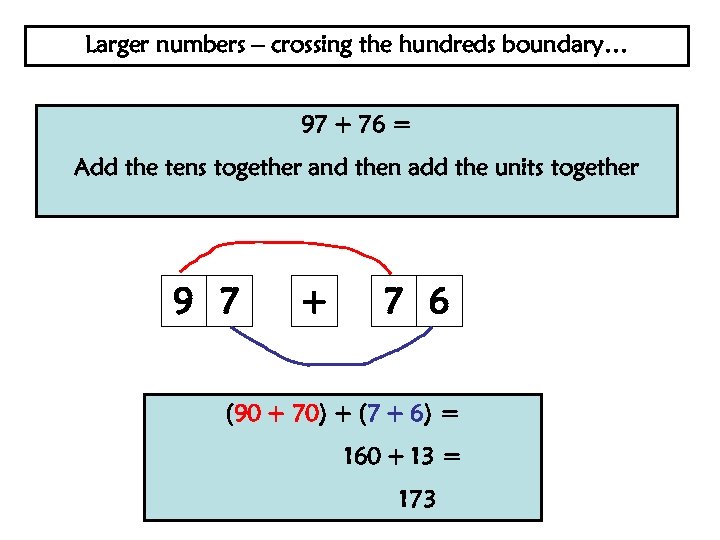Larger numbers – crossing the hundreds boundary… 97 + 76 = Add the tens together and then add the units together 9 7 + 7 6 (90 + 70) + (7 + 6) = 160 + 13 = 173

Vertical Layouts – Formal Written Methods (Year 4 ish)

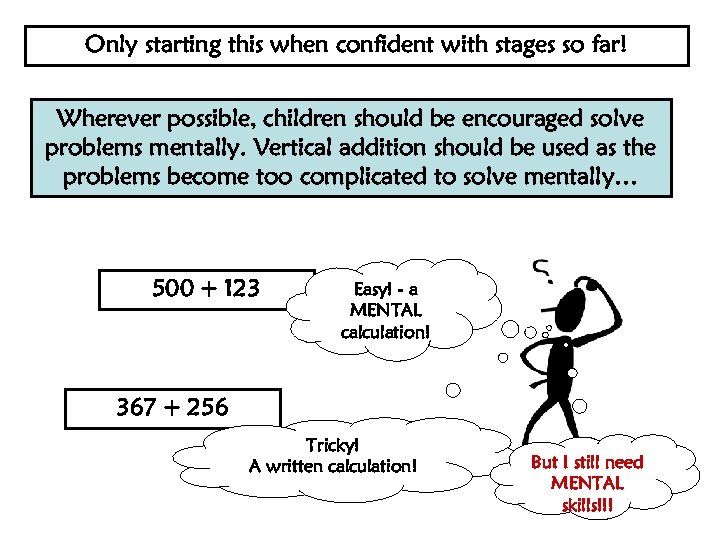Only starting this when confident with stages so far! Wherever possible, children should be encouraged solve problems mentally. Vertical addition should be used as the problems become too complicated to solve mentally… 500 + 123 Easy! - a MENTAL calculation! 367 + 256 Tricky! A written calculation! But I still need MENTAL skills!!!

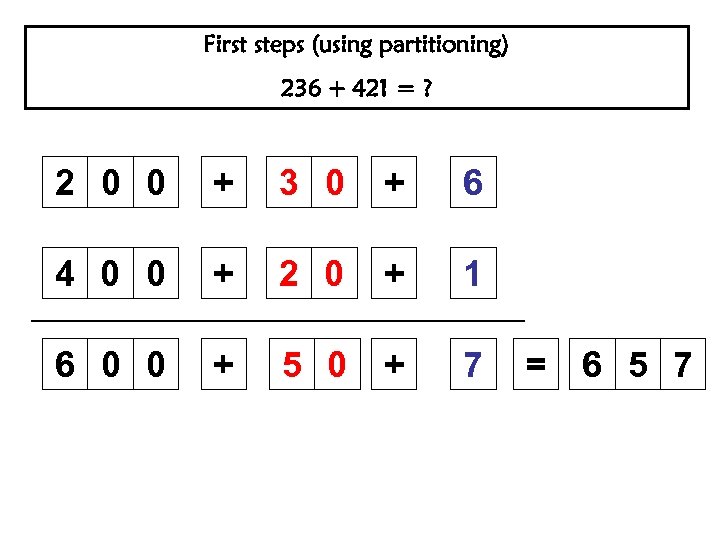First steps (using partitioning) 236 + 421 = ? 2 0 0 + 3 0 + 6 4 0 0 + 2 0 + 1 6 0 0 + 5 0 + 7 = 6 5 7

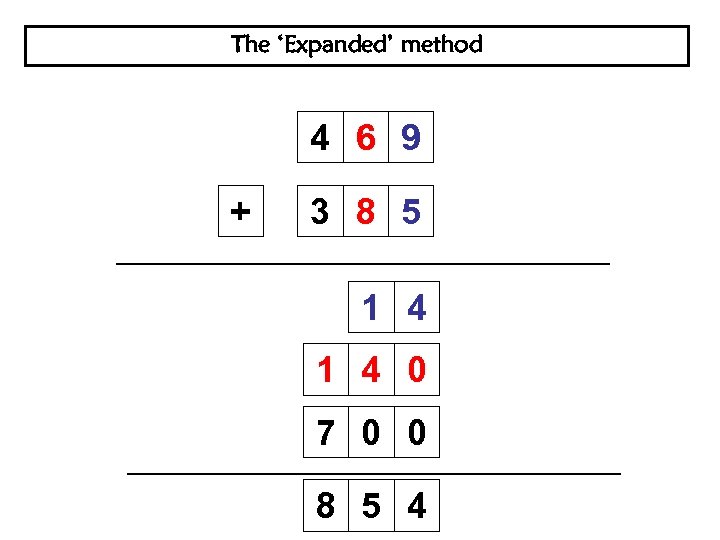The ‘Expanded’ method 4 6 9 + 3 8 5 1 4 0 7 0 0 8 5 4

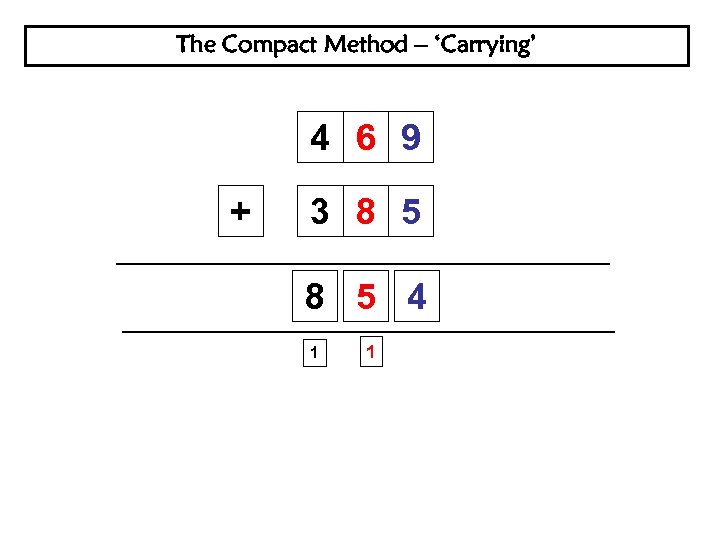The Compact Method – ‘Carrying’ 4 6 9 + 3 8 5 4 1 1

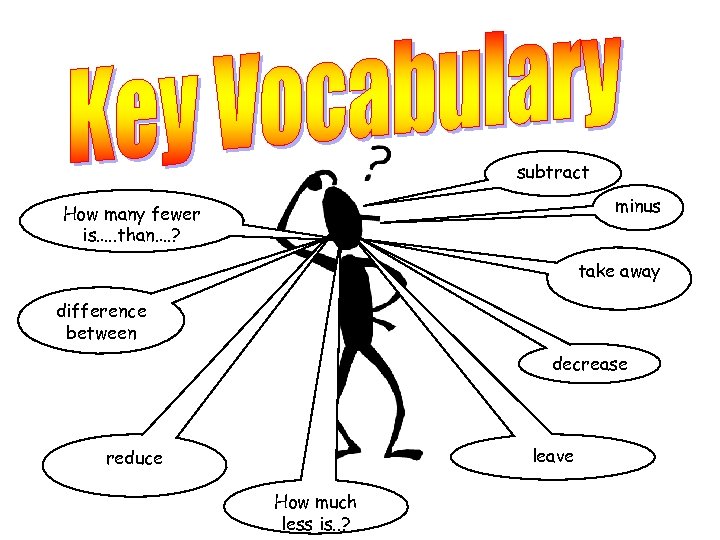subtract minus How many fewer is…. . than…. ? take away difference between decrease leave reduce How much less is. . ?

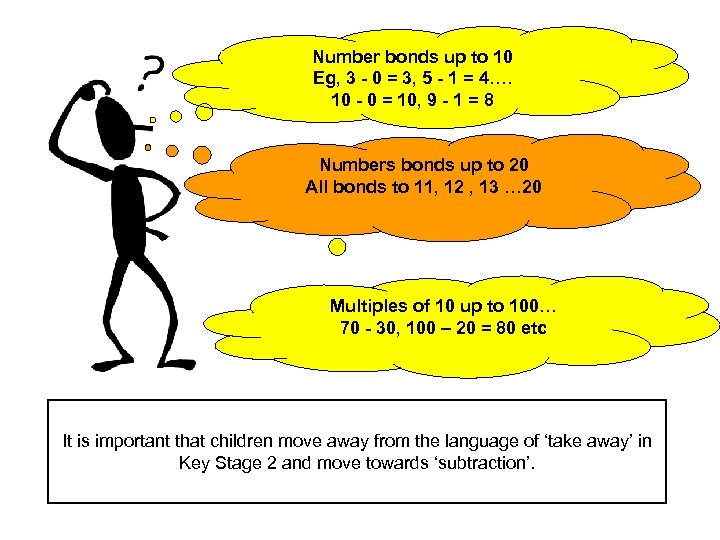Number bonds up to 10 Eg, 3 - 0 = 3, 5 - 1 = 4…. 10 - 0 = 10, 9 - 1 = 8 Numbers bonds up to 20 All bonds to 11, 12 , 13 … 20 Multiples of 10 up to 100… 70 - 30, 100 – 20 = 80 etc It is important that children move away from the language of ‘take away’ in Key Stage 2 and move towards ‘subtraction’.

Counting back… …on a numberline

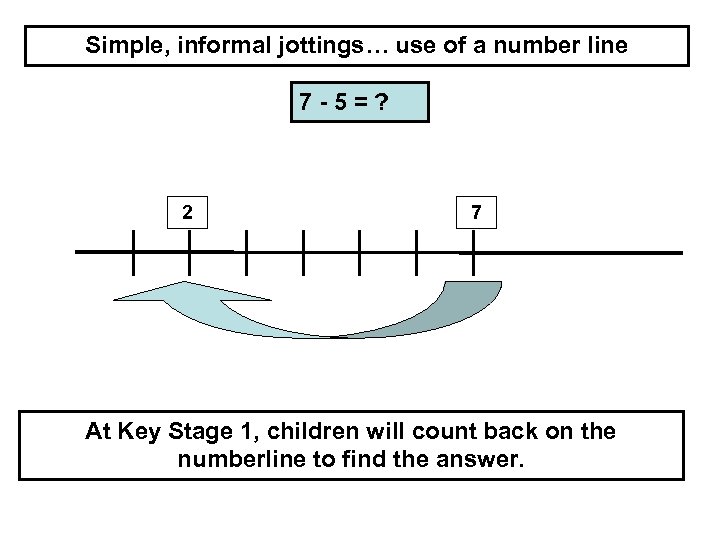Simple, informal jottings… use of a number line 7 -5=? 2 7 -5 At Key Stage 1, children will count back on the numberline to find the answer.

Counting on… …with a numberline

You buy an item for £ 8. You give a £ 20 note to the shopkeeper. What is the change? You buy an item for £ 15. 56 You give a £ 50 note to the shopkeeper. What is the change?

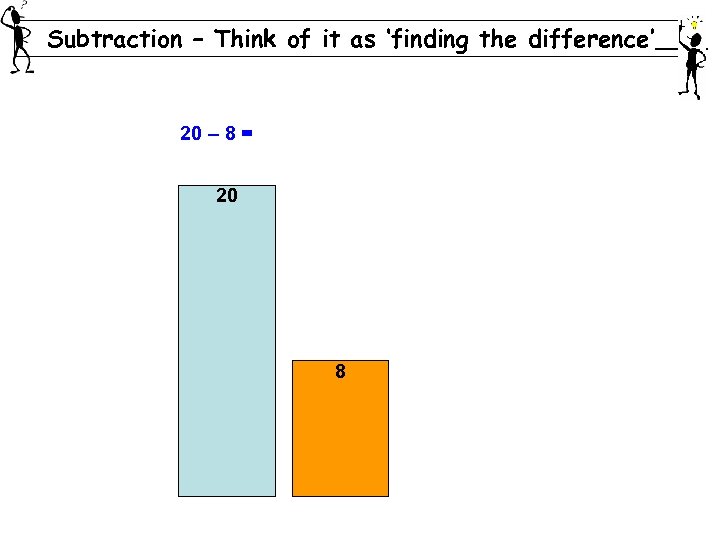Subtraction – Think of it as ‘finding the difference’ 20 – 8 = 20 8

20 – 8 = 20 8

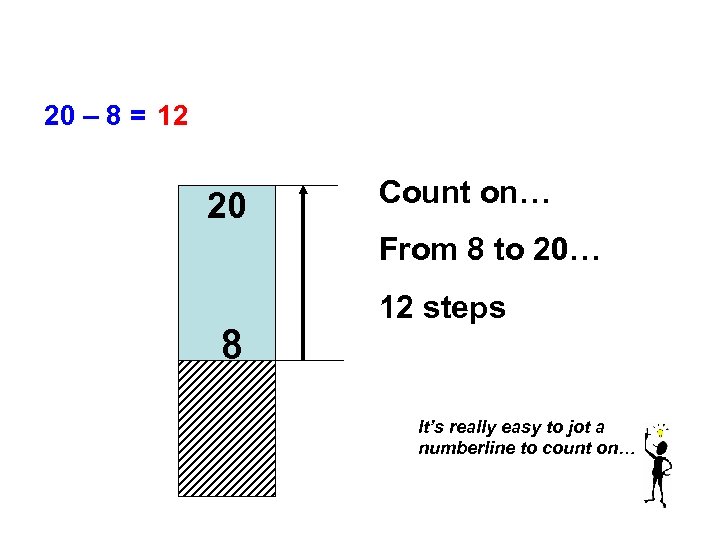20 – 8 = 12 20 Count on… From 8 to 20… 8 12 steps It’s really easy to jot a numberline to count on…

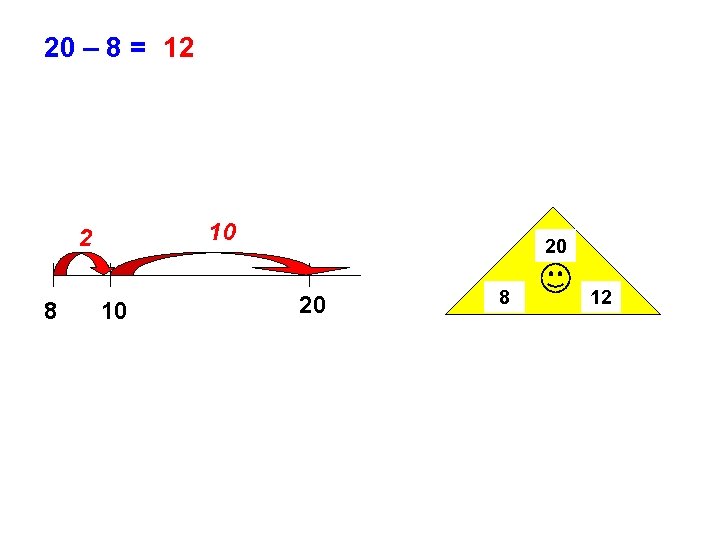20 – 8 = 12 10 2 8 10 20 20 8 12

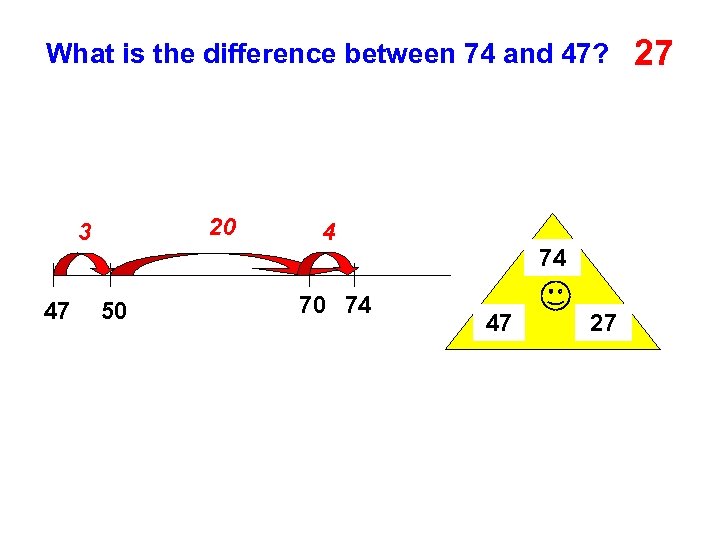What is the difference between 74 and 47? 20 3 47 50 4 70 74 74 47 27 27

You buy an item for £ 15. 56 You give a £ 50 note to the shopkeeper. What is the change? 4 p 15. 56 15. 60 £ 4 40 p 16. 00 £ 30 20. 00 50. 00 Then total all the jumps 4 p + 40 p + £ 4 + £ 30 = £ 34. 44 Jumps can be labelled with pounds and pence notation, or with decimal notation, leading to 0. 04 + 0. 40 + 4. 00 + 30. 00 = 34. 44 = £ 34. 44

Decrease 100 by 43 1 0 4 0 3 1 4 3 - SUBTRACTION MISCONCEPTIONS

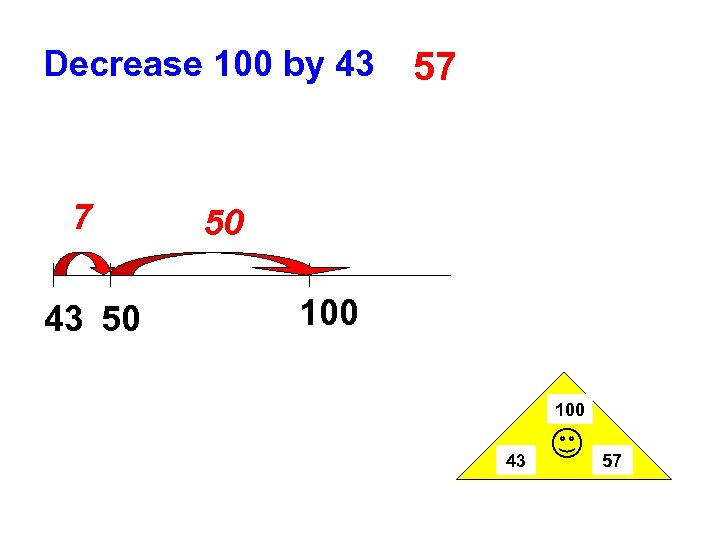Decrease 100 by 43 7 43 50 57 50 100 43 57

775 – 292 = - 7 2 7 9 5 2 3

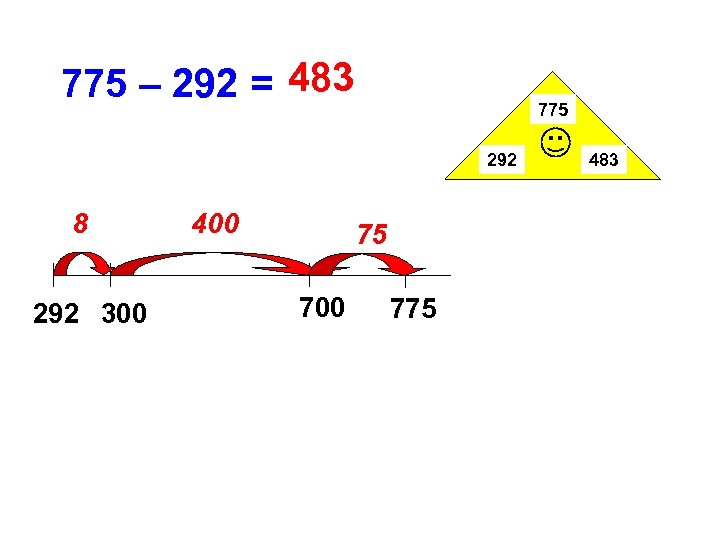775 – 292 = 483 775 292 8 292 300 400 75 700 775 483

The link between addition and subtraction

+ = - = - - +

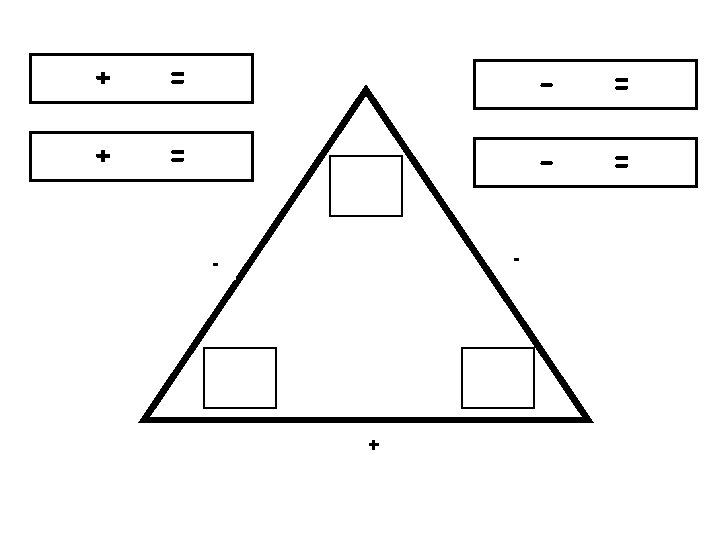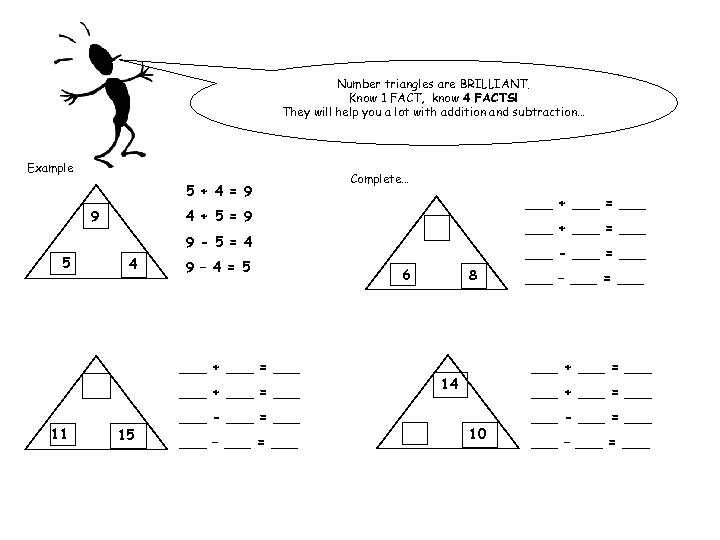Number triangles are BRILLIANT. Know 1 FACT, know 4 FACTS! They will help you a lot with addition and subtraction… Example 5 + 4 = 9 9 Complete… ___ + ___ = ___ 4 + 5 = 9 ___ + ___ = ___ 9 - 5 = 4 5 4 9 – 4 = 5 ___ + ___ = ___ 11 15 ___ - ___ = ___ – ___ = ___ - ___ = ___ 6 8 ___ – ___ = ___ + ___ = ___ 14 ___ + ___ = ___ 10 ___ - ___ = ___ – ___ = ___

Can I solve this mentally? Yes! CHECK!

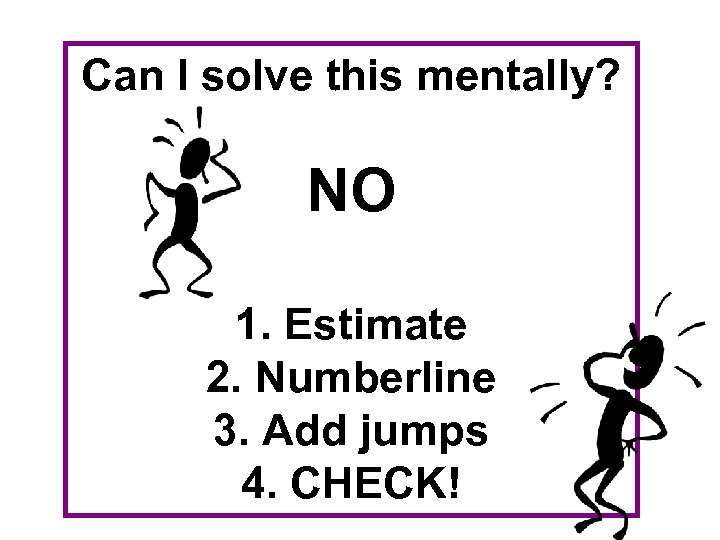Can I solve this mentally? NO 1. Estimate 2. Numberline 3. Add jumps 4. CHECK!

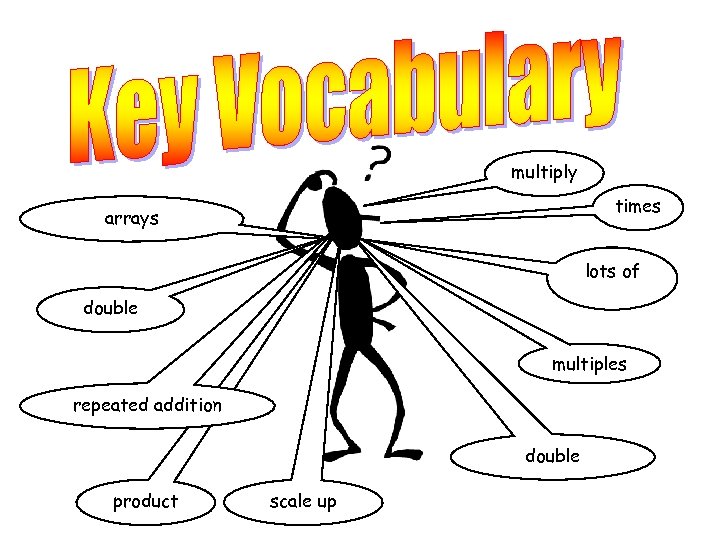multiply times arrays lots of double multiples repeated addition double product scale up

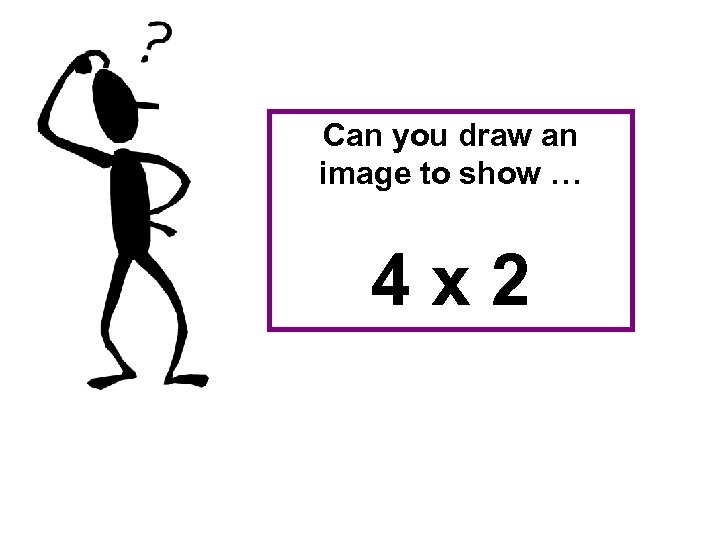Can you draw an image to show … 4 x 2

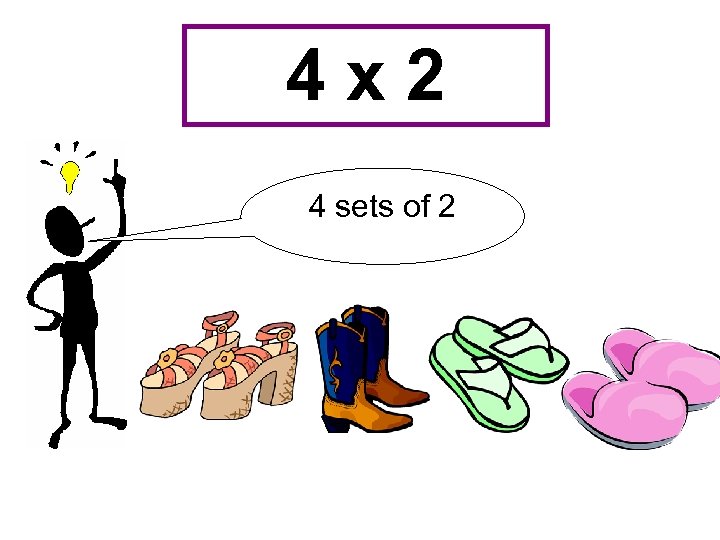4 x 2 4 sets of 2

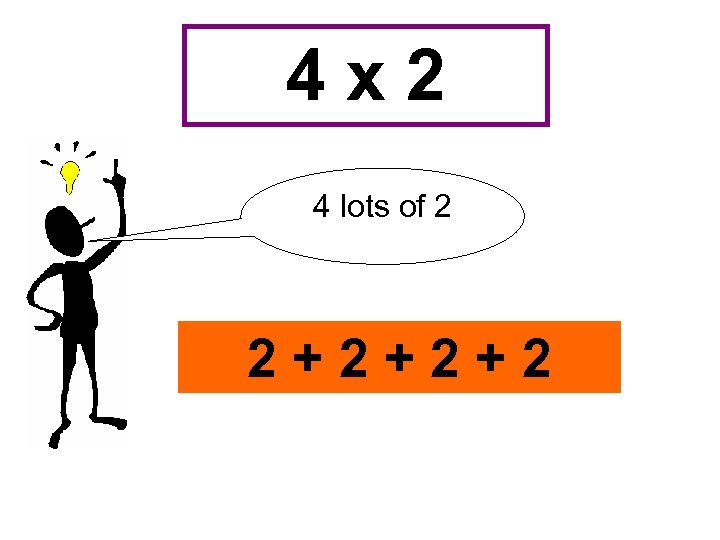4 x 2 4 lots of 2 2+2+2+2

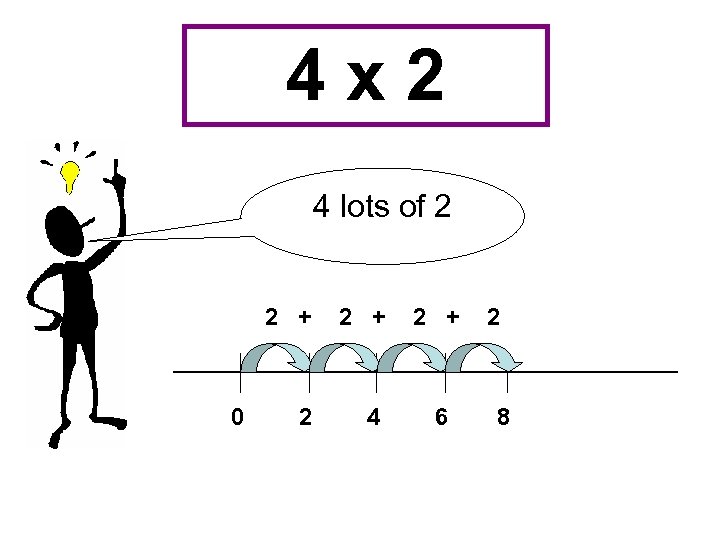4 x 2 4 lots of 2 2 + 0 2 + 2 4 2 + 6 2 8

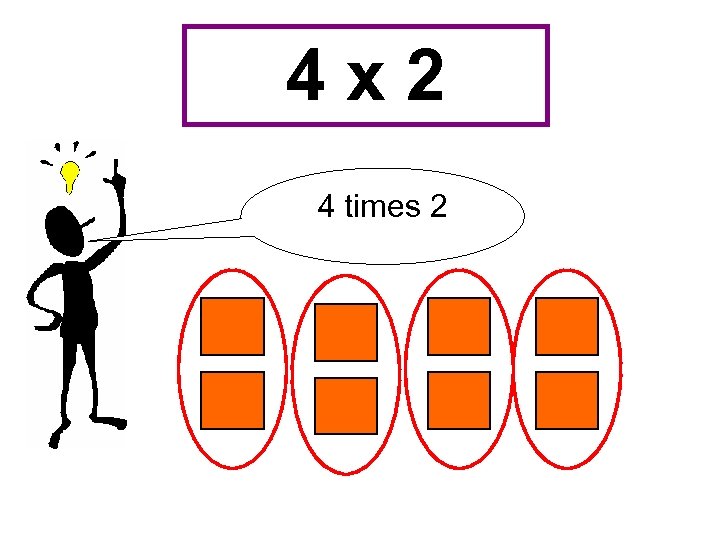4 x 2 4 times 2

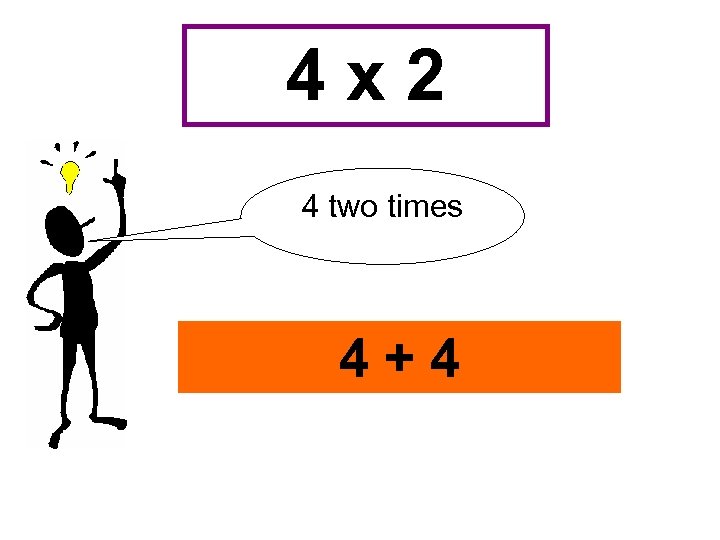4 x 2 4 two times 4+4

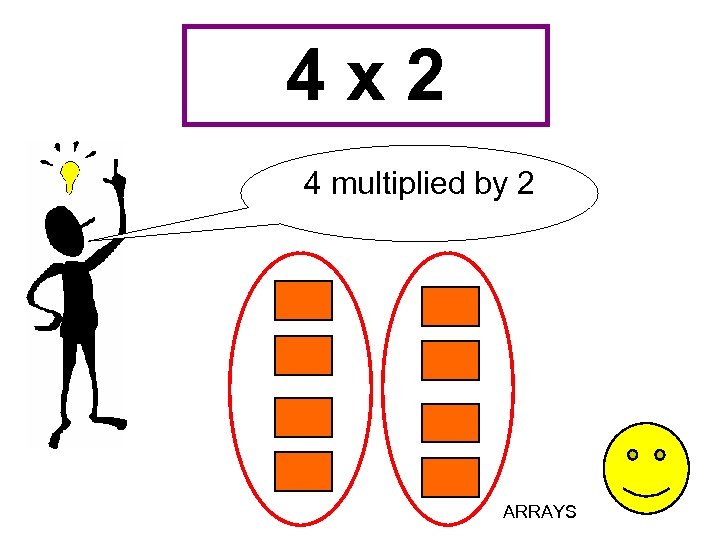4 x 2 4 multiplied by 2 ARRAYS

Fast, mental recall of times tables is really, really IMPORTANT!

Multiplying by 10 It is important that multiplying by 10 is not thought of as a case of ‘adding zeros’. It isn’t an inappropriate expression because adding zero actually leaves a number unchanged and the ‘add a zero rule’ fails when, for example, 0. 2 is multiplied by 10 (‘adding a zero’ results in 0. 20). Children need to understand that when you multiply by 10 the digits move one place to the left, leaving an empty space which is filled by zero (a place holder).

Multiplication facts Children will struggle with multiplication if they can’t recall multiplication facts. Knowing a multiplication table is much more than being able to recite it in order. It also means children should be able to respond quickly to oral or written questions phrased in a variety of ways, e. g. • What are seven fives? • What is 7 times five? • 5 multiplied by 7 is… • How many fives in 35? • What would I multiply by five to get 35? • What are the factors of 35?

divide share quotient group remainders decimals divisor fractions

12 3 = 4 Sharing There are three children and 12 cakes. How many can they each have, if I share them out equally? Sharing 12 things equally into 3 piles. How many in each

12 3 = 4 Grouping There are 12 cakes. How many children can have three each? (How many threes are there in 12? )

Language and division • The sign represents both the sharing and grouping aspects of division • Encourage the children to read this as ‘divided by’ rather than ‘shared by’, • Even easier – ‘HOW MANY!’

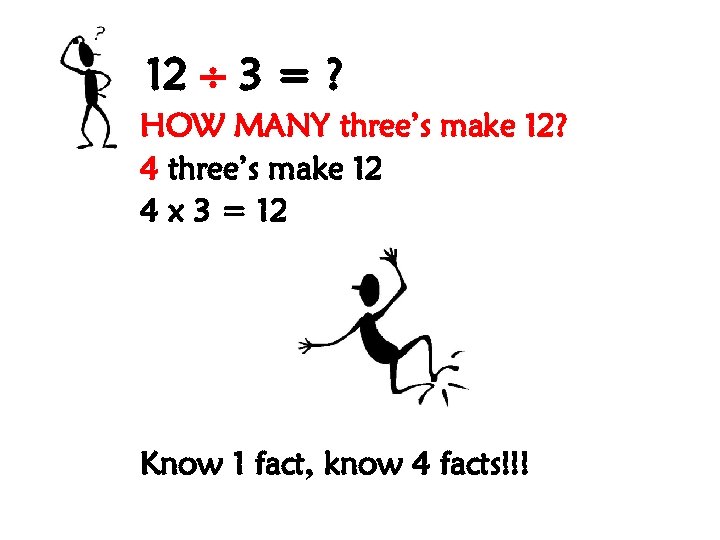12 3 = ? HOW MANY three’s make 12? 4 three’s make 12 4 x 3 = 12 Know 1 fact, know 4 facts!!!

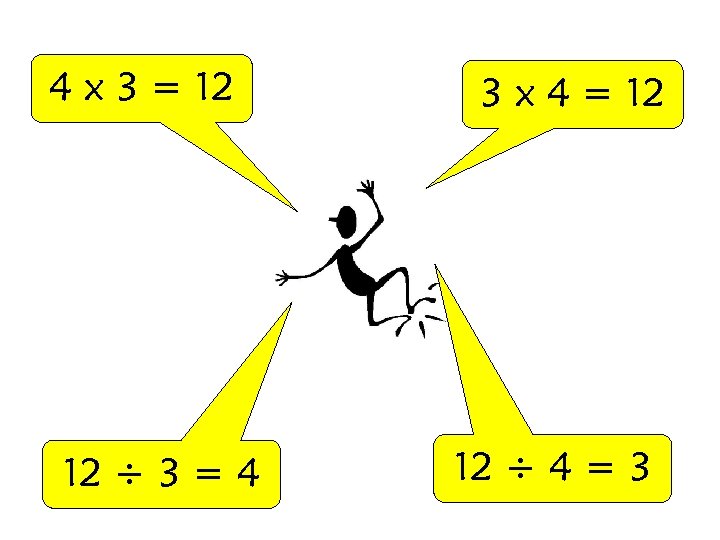4 x 3 = 12 12 ÷ 3 = 4 3 x 4 = 12 12 ÷ 4 = 3

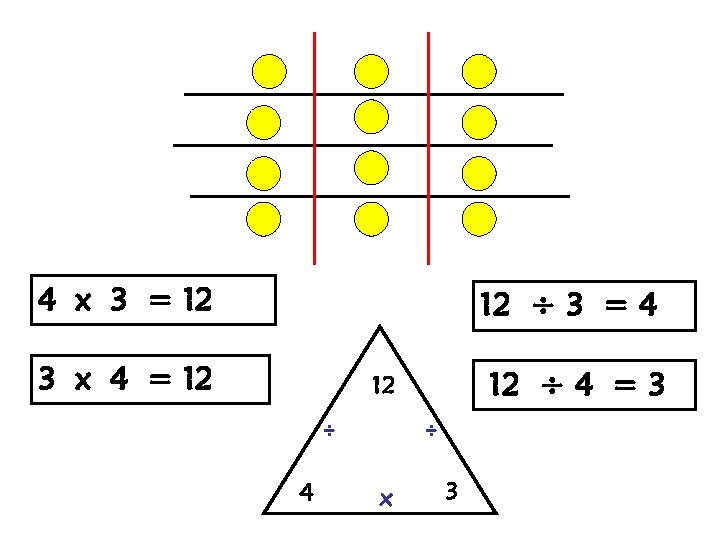4 x 3 = 12 12 ÷ 3 = 4 3 x 4 = 12 12 ÷ 4 = 3 12 ÷ 4 ÷ x 3

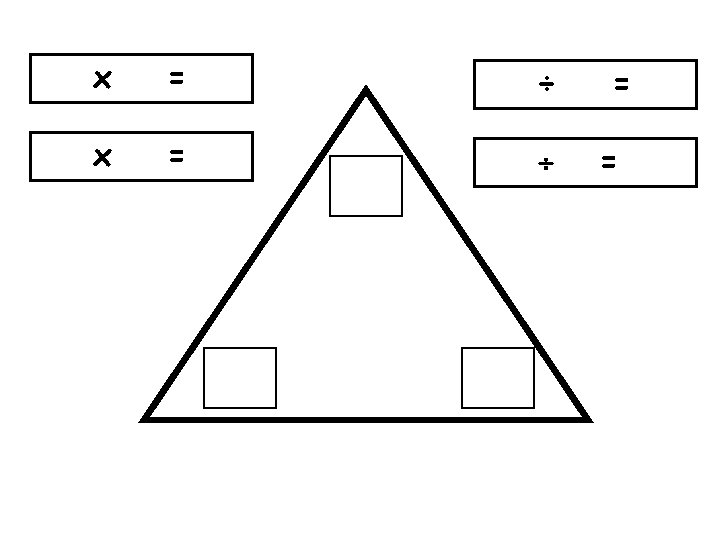x = ÷ = =

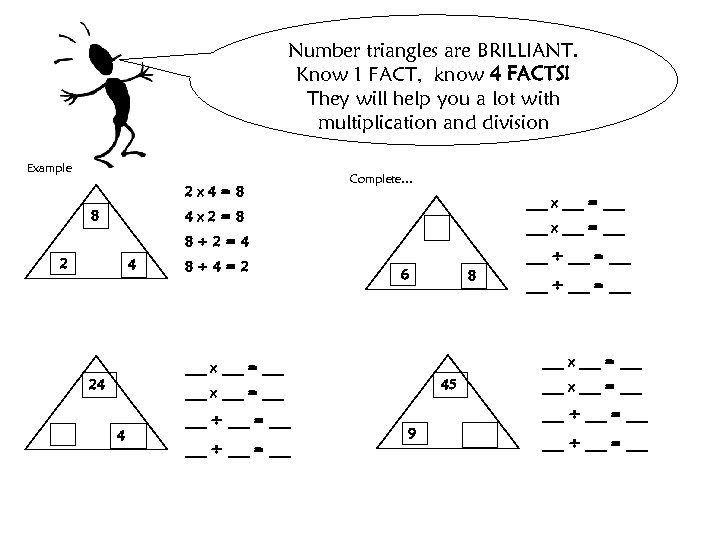Number triangles are BRILLIANT. Know 1 FACT, know 4 FACTS! They will help you a lot with multiplication and division Example 2 x 4=8 8 Complete… ___ x ___ = ___ 4 x 2=8 ___ x ___ = ___ 8÷ 2=4 2 4 8÷ 4=2 ___ ÷ ___ = ___ 6 8 ___ x ___ = ___ 24 45 ___ x ___ = ___ 4 ___ ÷ ___ = ___ x ___ = ___ ÷ ___ = ___ 9 ___ ÷ ___ = ___

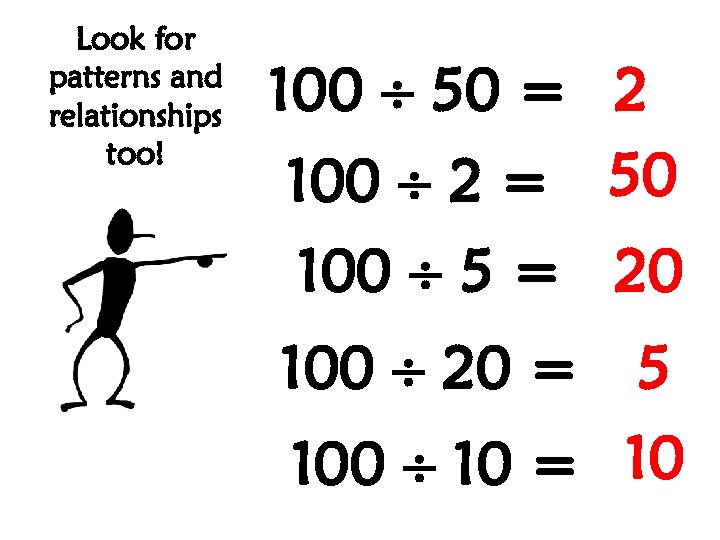Look for patterns and relationships too! 100 50 = 2 100 2 = 50 100 5 = 20 100 20 = 5 100 10 = 10

You’ll be laughing if you remember these simple facts… • dividing any number by 0 gives an answer of 0 eg, 6 ÷ 0 = 0 0 ÷ 59 = 0 • dividing any number by 1 leaves the number unchanged e. g, 12 1 =12 1, 346 ÷ 1 = 1, 346 Order does matter 16 2 does not equal 2 16 • division is the opposite of multiplication eg, 3 x 4 = 12 so 12 ÷ 4 = 3 • there will be remainders for some division calculations eg, 11 ÷ 2 = 5 and a remainder of 1

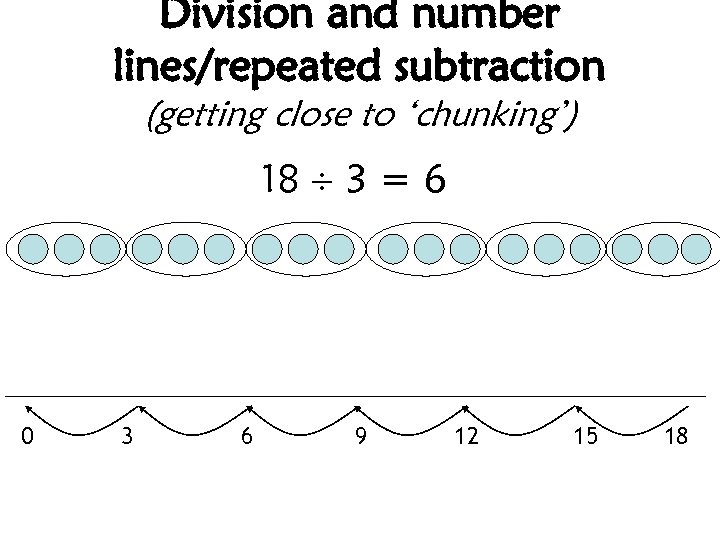Division and number lines/repeated subtraction (getting close to ‘chunking’) 18 3 = 6 0 3 6 9 12 15 18

Generally speaking, children are happier and more accurate when counting forwards… So think of 18 3 As ‘How many 3 s are in 18? ’ 0 3 6 9 12 15 18

Problem solving 1. I have 26 eggs. If 6 eggs fit in one box, how many boxes will I need for ALL the eggs? 2. There are 26 children in a P. E lesson. If teams of 6 are needed, how many full teams can be made?

The same basic calculation will be needed, but how we deal with the remainder will be different. So we need to calculate 26 ÷ 6 r 2 0 6 12 18 24 26 So the answer is 4 r 2 If we need to box up all the eggs, this means we need 5 boxes (but only 4 will be full) If we need teams of 6 children in P. E. , we can only have 4 teams, with 2 children left out.

Fractions! A whole session by itself but… 3 4 Know that it is possible to divide a smaller number by a larger number Know that the line in the middle of a fraction means ‘divided by’ Know how to work out a fraction as a decimal on a calculator

http: //www. woodlands-junior. kent. sch. uk/maths/

Very well done everyone! Thank you for your time! A favour please…