Welcome to MM 207 Statistics Hypothesis Testing

Welcome to MM 207 – Statistics Hypothesis Testing with One Sample Chapter 7 7. 1 – 7. 4 Anthony J. Feduccia

Chapter Outline • 7. 1 Introduction to Hypothesis Testing • 7. 2 Hypothesis Testing for the Mean (Large Samples) • 7. 3 Hypothesis Testing for the Mean (Small Samples) • 7. 4 Hypothesis Testing for Proportions • 0 mit Section 7. 5 Larson/Farber 4 th ed. 2

Guidelines -- Hypothesis Testing Steps: • State H 0 and Ha. • Specify the level of significance alpha . • Determine the test statistic, either z or t. Find the test statistic using the given data. • Find the P-value or the critical value(s) z 0 or t 0. Use the method specified in the problem statement. • Define the rejection region using either the P-value method or critical values from the Normal distribution. • Make a decision to reject or fail to reject the null hypothesis. • Interpret the decision in the context of the original claim.

Section 7. 1 Objectives • State a null hypothesis and an alternative hypothesis • Identify type I and type I errors and interpret the level of significance • Determine whether to use a one-tailed or twotailed statistical test and find a p-value • Make and interpret a decision based on the results of a statistical test Larson/Farber 4 th ed. 4

Hypothesis Tests Hypothesis test • A process that uses sample statistics to test a claim about the value of a population parameter. • For example: An automobile manufacturer advertises that its new hybrid car has a mean mileage of 50 miles per gallon. To test this claim, a sample would be taken. If the sample mean differs enough from the advertised mean, you can decide the advertisement is wrong. Larson/Farber 4 th ed. 5

Hypothesis Tests Statistical hypothesis • A statement, or claim, about a population parameter. • Need a pair of hypotheses • one that represents the claim • the other, its complement • When one of these hypotheses is false, the other must be true. Larson/Farber 4 th ed. 6

Example: Stating the Null and Alternative Hypotheses Write the claim as a mathematical sentence. State the null and alternative hypotheses and identify which represents the claim. 1. A university publicizes that the proportion of its students who graduate in 4 years is 82%. Solution: H 0: p = 0. 82 Equality condition (Claim) Ha: p ≠ 0. 82 Complement of H 0 Larson/Farber 4 th ed. 7

Example: Stating the Null and Alternative Hypotheses Write the claim as a mathematical sentence. State the null and alternative hypotheses and identify which represents the claim. 2. A water faucet manufacturer announces that the mean flow rate of a certain type of faucet is less than 2. 5 gallons per minute. Solution: H 0: μ ≥ 2. 5 gallons per minute Ha: μ < 2. 5 gallons per minute Larson/Farber 4 th ed. Complement of Ha Inequality (Claim) condition 8

Example: Stating the Null and Alternative Hypotheses Write the claim as a mathematical sentence. State the null and alternative hypotheses and identify which represents the claim. 3. A cereal company advertises that the mean weight of the contents of its 20 -ounce size cereal boxes is more than 20 ounces. Solution: H 0: μ ≤ 20 ounces Ha: μ > 20 ounces Complement of Ha Inequality (Claim) condition Larson/Farber 4 th ed. 9

1. a. A candidate for mayor of a city claims to be favored by at least half the voters. Test this candidates claim. (4 points) claim: H 0 : Ha : Test : b. The mean age of bus drivers in Chicago is 50. 9 years. Test the claim that the mean age differs from this. (4 points) claim: H 0 : Ha : Test :

Types of Errors • No matter which hypothesis represents the claim, always begin the hypothesis test assuming that the equality condition in the null hypothesis is true. • At the end of the test, one of two decisions will be made: – reject the null hypothesis – fail to reject the null hypothesis • Because your decision is based on a sample, there is the possibility of making the wrong decision. Larson/Farber 4 th ed. 11

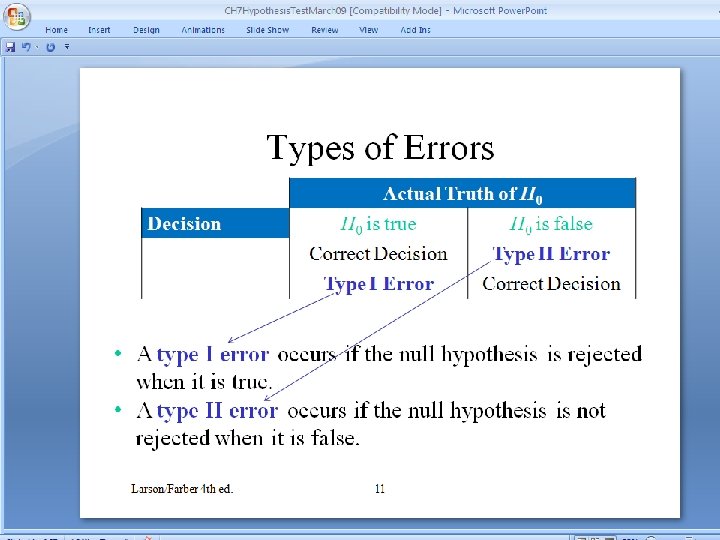Types of Errors Decision Do not reject H 0 Reject H 0 Actual Truth of H 0 is true H 0 is false Correct Decision Type II Error Type I Error Correct Decision • A type I error occurs if the null hypothesis is rejected when it is true. • A type II error occurs if the null hypothesis is not rejected when it is false. Larson/Farber 4 th ed. 12

P-values (see page 370) P-value (or probability value) • Find test statistic from the data. Either a z or a t. • For a left-tail test: p value is area to the left of the test statistic. • For a right-tail test: p value is area to the right of the test statistic (recall tables give area to the left) • For a double-tail test: p value is twice the area to the left of a negative test statistic or twice the area to the right of a positive test statistic. 13

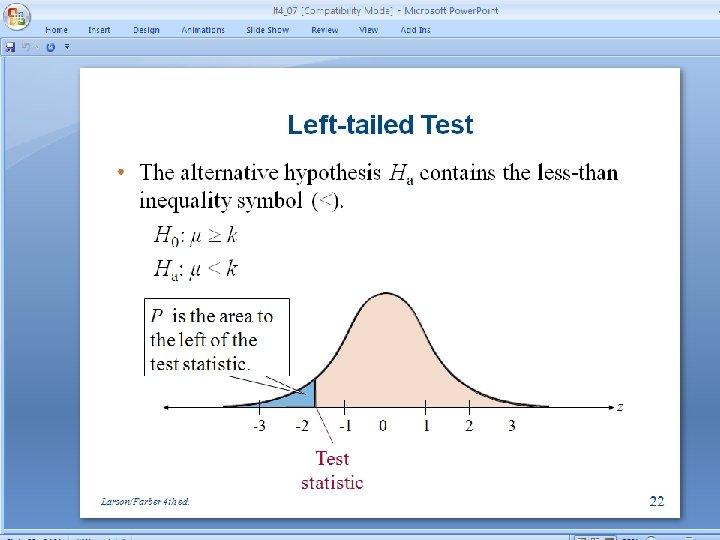Left-tailed Test • The alternative hypothesis Ha contains the lessthan inequality symbol (<). H 0: μ k Ha : μ < k P is the area to the left of the test statistic. -3 -2 -1 Test statistic 0 14 1 2 3 z

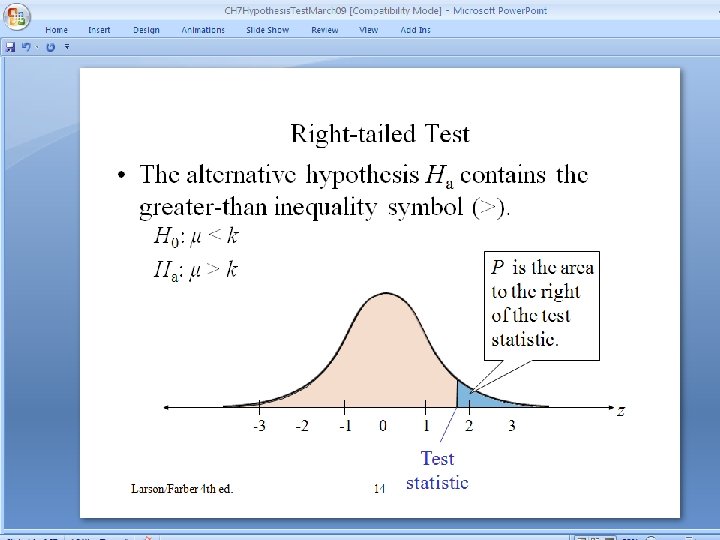Right-tailed Test • The alternative hypothesis Ha contains the greater-than inequality symbol (>). H 0: μ ≤ k Ha : μ > k P is the area to the right of the test statistic. -3 Larson/Farber 4 th ed. -2 -1 0 15 1 2 Test statistic 3 z

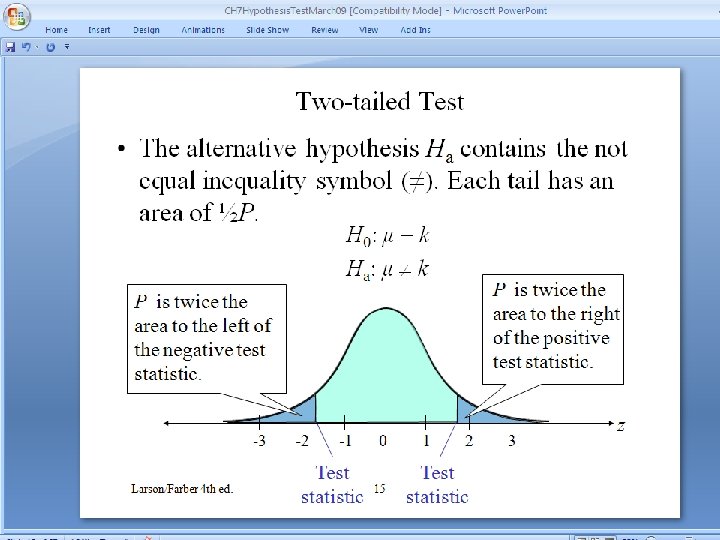Two-tailed Test • The alternative hypothesis Ha contains the not equal inequality symbol (≠). Each tail has an area of ½P. H 0: μ = k Ha : μ k P is twice the area to the right of the positive test statistic. P is twice the area to the left of the negative test statistic. -3 Larson/Farber 4 th ed. -2 -1 Test statistic 0 16 1 2 Test statistic 3 z

Example Using P-Value In an advertisement, a pizza shop claims that its mean delivery time is less than 30 minutes. A random selection of 36 delivery times has a sample mean of 28. 5 minutes and a standard deviation of 3. 5 minutes. Is there enough evidence to support the claim at = 0. 01? Use a P-value. Larson/Farber 4 th ed. 17

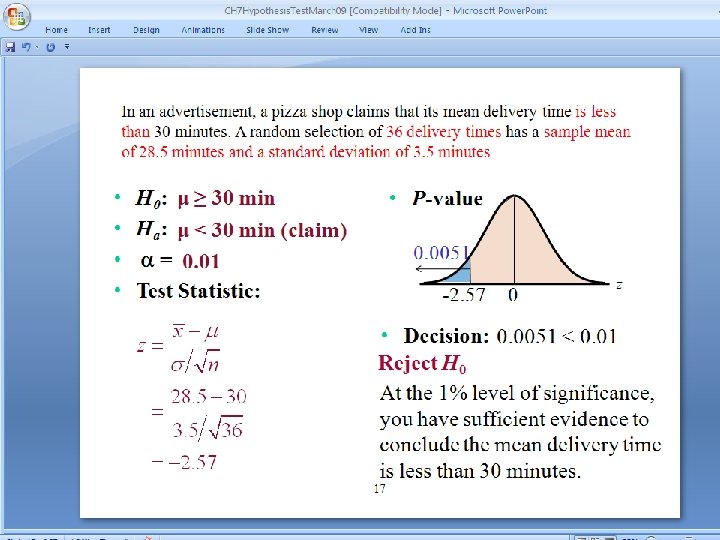In an advertisement, a pizza shop claims that its mean delivery time is less than 30 minutes. A random selection of 36 delivery times has a sample mean of 28. 5 minutes and a standard deviation of 3. 5 minutes • • H 0: μ ≥ 30 min Ha: μ < 30 min (claim) = 0. 01 Test Statistic: • P-value 0. 0051 -2. 57 0 z • Decision: 0. 0051 < 0. 01 Reject H 0 At the 1% level of significance, you have sufficient evidence to conclude the mean delivery time is less than 30 minutes. 18

An alternative approach to Hypothesis testing Using Rejection regions (page 386) Employees in a large accounting firm claim that the mean salary of the firm’s accountants is less than that of its competitor’s, which is $45, 000. A random sample of 30 of the firm’s accountants has a mean salary of $43, 500 with a standard deviation of $5200. At α = 0. 05, test the employees’ claim. Larson/Farber 4 th ed. 19

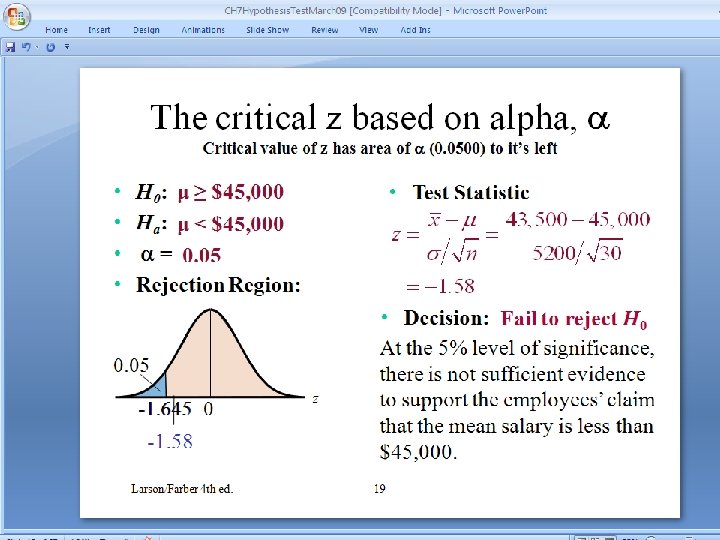The critical z based on alpha, Critical value of z has area of (0. 0500) to it’s left • • H 0: μ ≥ $45, 000 Ha: μ < $45, 000 = 0. 05 Rejection Region: • Test Statistic 0. 05 -1. 645 0 -1. 58 Larson/Farber 4 th ed. z • Decision: Fail to reject H 0 At the 5% level of significance, there is not sufficient evidence to support the employees’ claim that the mean salary is less than $45, 000. 20

Example: Testing μ with a Small Sample A used car dealer says that the mean price of a 2005 Honda Pilot LX is at least $23, 900. You suspect this claim is incorrect and find that a random sample of 14 similar vehicles has a mean price of $23, 000 and a standard deviation of $1113. Is there enough evidence to reject the dealer’s claim at α = 0. 05? Assume the population is normally distributed. (Adapted from Kelley Blue Book) Larson/Farber 4 th ed. 21

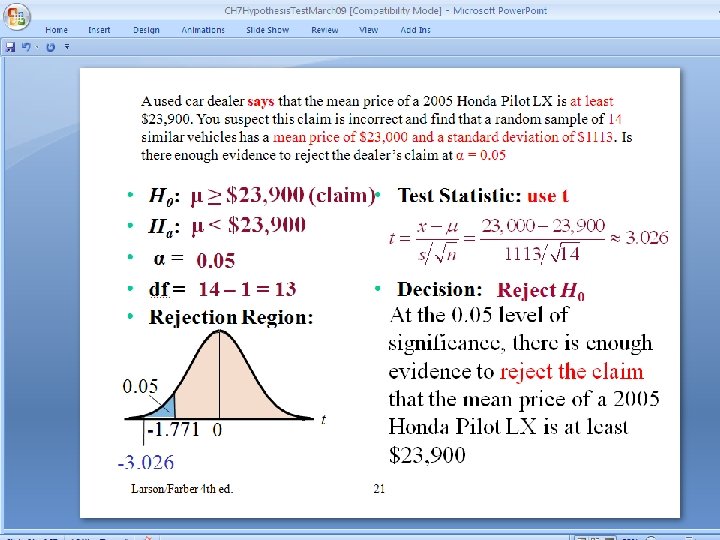A used car dealer says that the mean price of a 2005 Honda Pilot LX is at least $23, 900. You suspect this claim is incorrect and find that a random sample of 14 similar vehicles has a mean price of $23, 000 and a standard deviation of $1113. Is there enough evidence to reject the dealer’s claim at α = 0. 05 • • • Solution: Testing μ with a Small Sample H 0: μ ≥ $23, 900 (claim) Test Statistic: use t • Ha: μ < $23, 900 α = 0. 05 df = 14 – 1 = 13 • Decision: Reject H 0 At the 0. 05 level of Rejection Region: significance, there is enough evidence to reject the claim that the mean price of a 2005 Honda Pilot LX is at least $23, 900 0. 05 -1. 771 0 t -3. 026 Larson/Farber 4 th ed. 22

• A fast food outlet claims that the mean waiting time in line is less than 4. 9 minutes. A random sample of 60 customers yield a sample mean of 4. 8 minutes. From past studies it is know that the standard deviation is 0. 6 minutes. At alpha = 0. 05, test the fast food outlet’s claim a. Use the critical value z 0 method from the normal distribution. Known: u = 4. 9, x bar = 4. 8, sigma = 0. 6; alpha = 0. 05; n =60 Ho: Ha: Test statistic: Critical zo Rejection Region: Decision:

Use the P-value method. • H 0 : claim Ha : Test statistic • : • P-value or critical z 0 or t 0. P-value = P(z < -1. 29 ) = 0. 0985 • Rejection Region: If P-value <= , then reject H 0. If P-value > , then fail to reject H 0. • Decision: = 0. 05 and P-value = 0. 0985 and since 0. 0985 > 0. 05, then we fail to reject H 0. • Interpretation:

z-Test for a Population Proportion • A statistical test for a population proportion. • Can be used when a binomial distribution is given such that np 5 and nq 5. • The test statistic is the sample proportion. • The standardized test statistic is z. Larson/Farber 4 th ed. 25

Example: Hypothesis Test for Proportions Zogby International claims that 45% of people in the United States support making cigarettes illegal within the next 5 to 10 years. You decide to test this claim and ask a random sample of 200 people in the United States whether they support making cigarettes illegal within the next 5 to 10 years. Of the 200 people, 49% support this law. At α = 0. 05 is there enough evidence to reject the claim? Solution: • Verify that np ≥ 5 and nq ≥ 5. np = 200(0. 45) = 90 and nq = 200(0. 55) = 110 Larson/Farber 4 th ed. 26

Use Normal z for proportions • • H 0: p = 0. 45 Ha: p ≠ 0. 45 = 0. 05 Rejection Region: 0. 025 -1. 96 • Test Statistic 0. 025 0 1. 96 1. 14 Larson/Farber 4 th ed. z • Decision: Fail to reject H 0 At the 5% level of significance, there is not enough evidence to reject the claim that 45% of people in the U. S. support making cigarettes illegal within the next 5 to 10 years. 27