Weighted Partonomy-Taxonomy Trees with Local Similarity Measures for

Weighted Partonomy-Taxonomy Trees with Local Similarity Measures for Semantic Buyer-Seller Matchmaking By: Lu Yang March 16, 2005 1

Outline l l l Motivation Similarity Measures Partonomy Similarity Algorithm – – – l l Experimental Results Node Label Similarity – – l 2 Tree representation Tree simplicity Partonomy similarity Inner-node similarity Leaf-node similarity Conclusion

Motivation e-business, e-learning … l Buyer-Seller matching l Metadata for buyers and sellers l – – l 3 Keywords/keyphrases Tree similarity

Similarity measures l Similarity measures apply to many research areas – l CBR (Case Based Reasoning), information retrieval, pattern recognition, image analysis and processing, NLP (Natural Language Processing), bioinformatics, search engine, e. Commerce and so on In e-Commerce – Product P satisfies demand D ? l l l 4 Now, a “How similar? ” question! Is it an “All or Nothing” question? Additional knowledge needed Bridge the gap between demand product descriptions

Similarity measures (Cont’d) l Numerical modeling of similarity – – A similarity measure on a set M is a real function sim: M 2 ® [0, 1] Similarity measures have following properties Reflexivity " x Î M: sim(x, x) = 1 Symmetry 5 iff " x, y Î M: sim(x, y) = sim(y, x)

Similarity measures – distance measures l An opposite notion of similarity measures A distance measure on a set M is a real valued function d: M 2 ® IR+ l Distance measures have following properties l – Reflexivity " x Î M d(x, x) = 0 – Symmetry iff " x, y Î M d(x, y) = d(y, x) – Triangle Inequality iff " x, y Î M 6 d(x, y) = 0 ® x = y " x, y, z Î M d(x, y) + d(y, z) ³ d(x, z)

Similarity measures – distance measures l Transformation of similarity measures and distance measures – If a bijective, order inverting mapping f: [0, 1] ® [0, 1] exists with f(d(x, y)) = sim(x, y) then sim and d are compatible 7

Similarity measures – global and local l Global measures are defined on the whole object – l Local measures are defined on details (e. g. the domains of some attribute) – – 8 reflect the task and have a pragmatic character reflect technical and domain character task independent

Similarity measures – global and local l Local to global – – 9 each object A is constructed from so-called “components” Ai by some construction process C(Ai |i Î n) = A given two objects A and B, simi(Ai, Bi) denotes the similarity of their ith components amalgamation function f sim(A, B) is the global similarity measure of A and B sim(A, B) = f(simi(Ai , Bi) |i Î n )

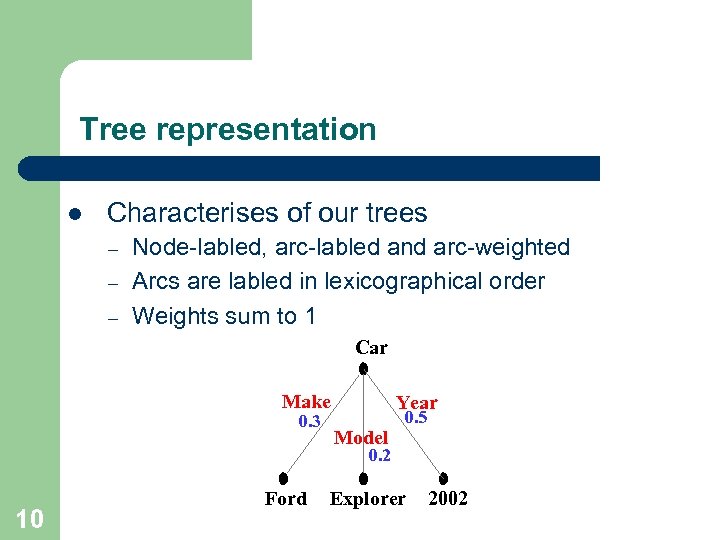Tree representation l Characterises of our trees – – – Node-labled, arc-labled and arc-weighted Arcs are labled in lexicographical order Weights sum to 1 Car Make 0. 3 Year Model 0. 5 0. 2 10 Ford Explorer 2002

Tree representation – serialization of trees Weighted Object-Oriented Rule. ML – XML attributes for arc weights and subelements for arc labels – Car MakeFord ModelExplorer Year2002 11 Tree serialization in WOO Rule. ML

Tree representation – Relfun version of tree cterm[ -opc[ctor[car]], -r[n[make], w[0. 3]][ind[ford]], -r[n[model], w[0. 2]][ind[explorer], -r[n[year], w[0. 5]][ind[2002]] ] 12

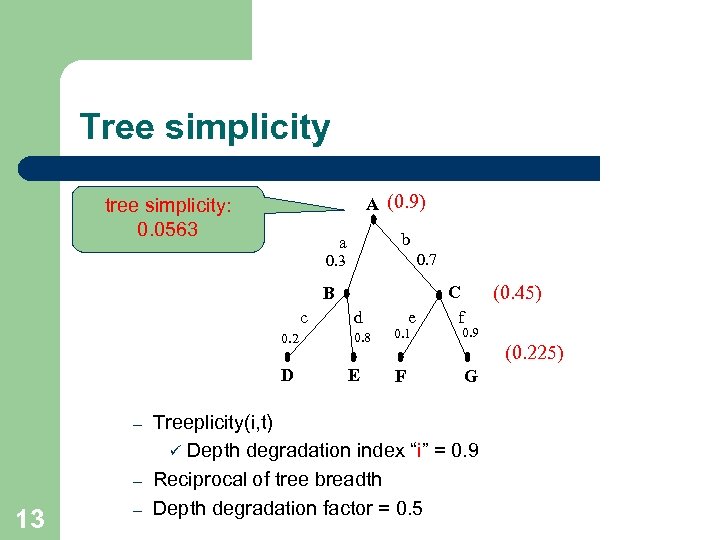Tree simplicity A (0. 9) tree simplicity: 0. 0563 b a 0. 7 0. 3 B c 0. 2 D – – 13 – d 0. 8 E e 0. 1 F (0. 45) C f 0. 9 (0. 225) G Treeplicity(i, t) ü Depth degradation index “i” = 0. 9 Reciprocal of tree breadth Depth degradation factor = 0. 5

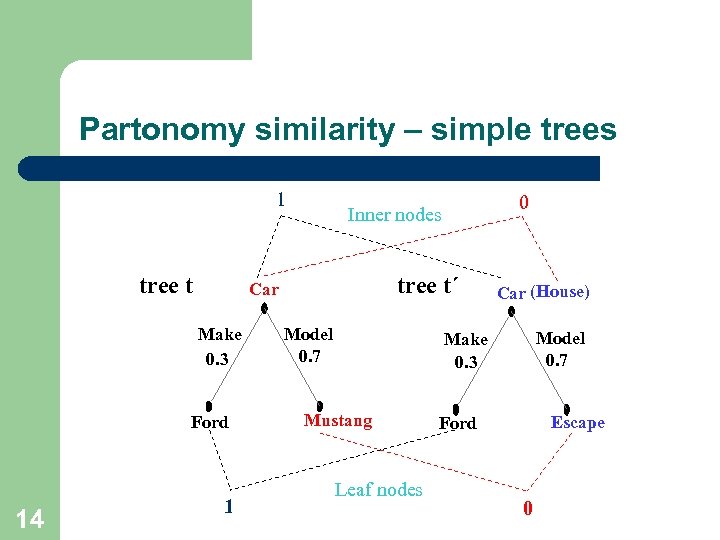Partonomy similarity – simple trees 1 tree t Ford 14 tree t´ Car Make 0. 3 1 0 Inner nodes Model 0. 7 Car (House) Model 0. 7 Make 0. 3 Mustang Leaf nodes Escape Ford 0

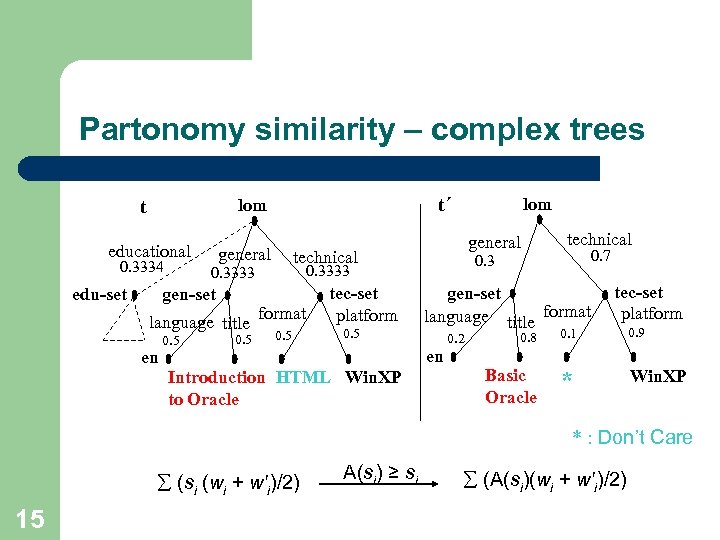Partonomy similarity – complex trees t t´ lom educational 0. 3334 edu-set general language title en 0. 5 general technical format 0. 5 tec-set platform 0. 5 0. 7 gen-set language title format en Introduction HTML Win. XP to Oracle technical 0. 3333 gen-set lom tec-set platform 0. 8 0. 1 0. 9 Basic Oracle 0. 2 * Win. XP * : Don’t Care (si (wi + w'i)/2) 15 A(si) ≥ si (A(si)(wi + w'i)/2)

Partonomy similarity – main recursive functions l Three main recursive functions (Relfun) – – Treemap(l, l'): Recursively maps two lists, l and l', of labeled and weighted arcs: descends into identical–labeled subtrees – 16 Treesim(t, t'): Recursively compares any (unordered) pair of trees Paremeters N and i Treeplicity(i, t): Decreases the similarity with decreasing simplicity

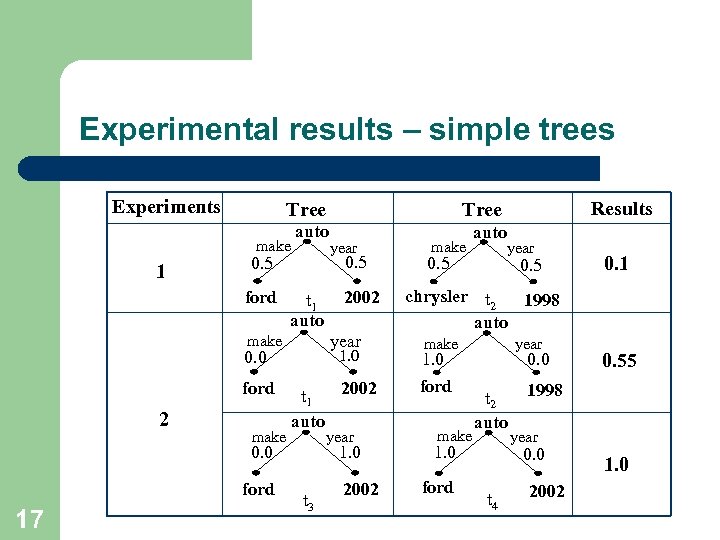Experimental results – simple trees Experiments Tree make 1 auto ford t 1 auto 1. 0 0. 0 2 make 2002 t 1 auto year 0. 0 ford 17 2002 year make ford year 0. 5 1. 0 t 3 Results Tree 2002 make auto year 0. 5 0. 1 chrysler t 2 1998 auto make year 1. 0 ford make 0. 0 t 2 auto 1. 0 ford 1998 year 0. 0 t 4 0. 55 2002 1. 0

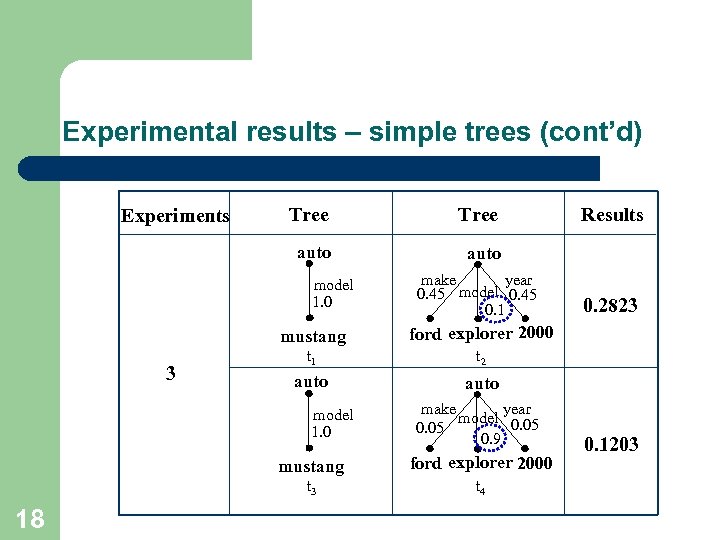Experimental results – simple trees (cont’d) Tree auto Experiments auto model 1. 0 year make 0. 45 model 0. 45 0. 1 mustang 3 t 2 auto model 1. 0 year make model 0. 05 0. 9 mustang ford explorer 2000 t 3 18 0. 2823 ford explorer 2000 t 1 Results t 4 0. 1203

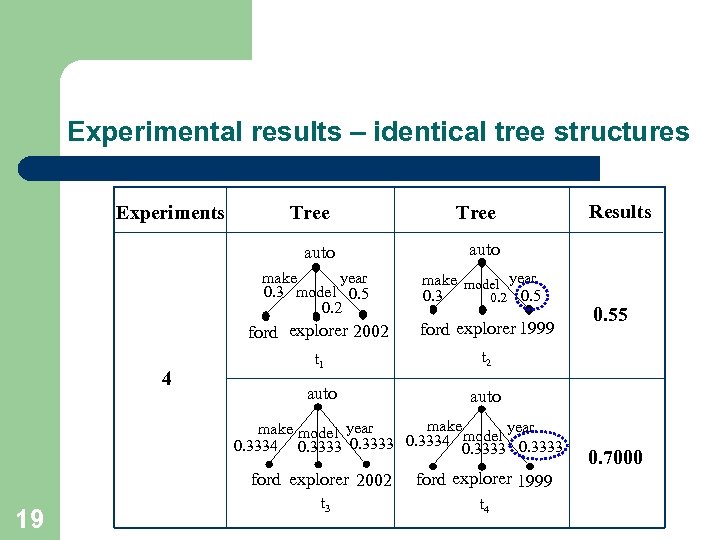Experimental results – identical tree structures Experiments Tree auto year make 0. 3 model 0. 5 0. 2 make model year 0. 3 0. 2 0. 5 ford explorer 2002 4 ford explorer 1999 t 1 auto 0. 55 t 2 auto make year make model year model 0. 3334 0. 3333 ford explorer 2002 19 Results ford explorer 1999 t 3 t 4 0. 7000

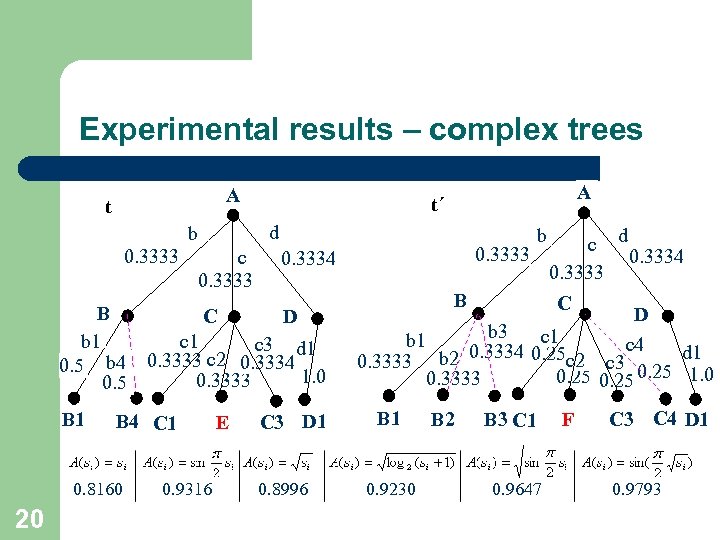Experimental results – complex trees A t d b 0. 3333 c 0. 3333 b B 4 C 1 0. 8160 20 0. 9316 E c d 0. 3333 0. 3334 B C D b 1 c 3 d 1 0. 5 b 4 0. 3333 c 2 0. 3334 1. 0 0. 3333 0. 5 B 1 A t´ C 3 D 1 0. 8996 B C D b 3 c 1 b 1 c 4 0. 3334 0. 25 c 2 d 1 0. 3333 b 2 c 3 0. 25 1. 0 0. 25 0. 3333 B 1 0. 9230 B 2 B 3 C 1 0. 9647 F C 3 C 4 D 1 0. 9793

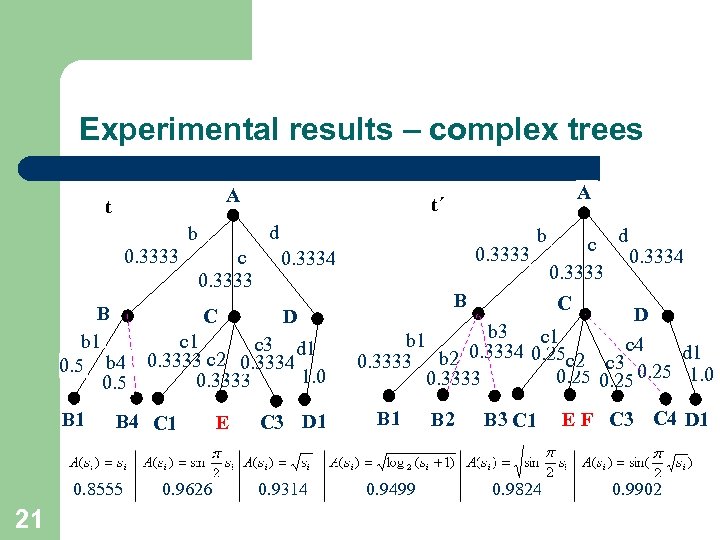Experimental results – complex trees A t d b 0. 3333 c 0. 3333 b B 4 C 1 0. 8555 21 0. 9626 E c d 0. 3333 0. 3334 B C D b 1 c 3 d 1 0. 5 b 4 0. 3333 c 2 0. 3334 1. 0 0. 3333 0. 5 B 1 A t´ C 3 D 1 0. 9314 B C D b 3 c 1 b 1 c 4 0. 3334 0. 25 c 2 d 1 0. 3333 b 2 c 3 0. 25 1. 0 0. 25 0. 3333 B 1 0. 9499 B 2 B 3 C 1 0. 9824 E F C 3 C 4 D 1 0. 9902

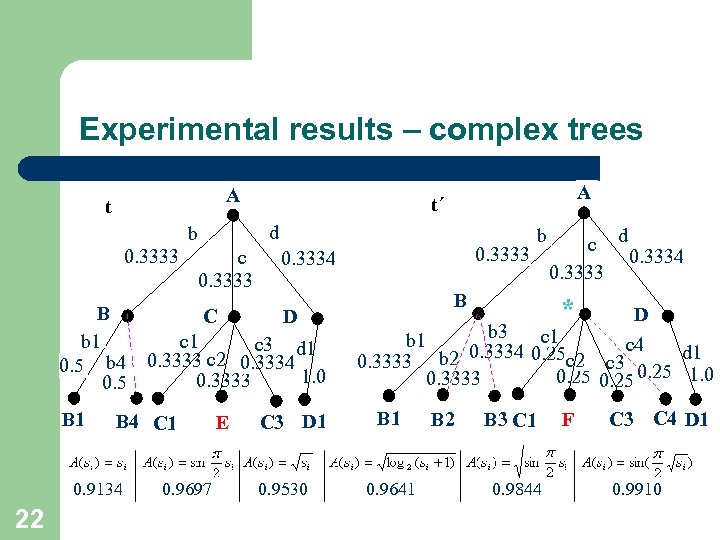Experimental results – complex trees A t d b 0. 3333 c 0. 3333 b B 4 C 1 0. 9134 22 0. 9697 E c d 0. 3333 0. 3334 B C D b 1 c 3 d 1 0. 5 b 4 0. 3333 c 2 0. 3334 1. 0 0. 3333 0. 5 B 1 A t´ C 3 D 1 0. 9530 B * D b 3 c 1 b 1 c 4 0. 3334 0. 25 c 2 d 1 0. 3333 b 2 c 3 0. 25 1. 0 0. 25 0. 3333 B 1 0. 9641 B 2 B 3 C 1 0. 9844 F C 3 C 4 D 1 0. 9910

Node label similarity l For both inner nodes and leaf nodes – Exact string matching binary result 0. 0 or 1. 0 – Permutation of strings “Java Programming” vs “Programming in Java” Number of identical words Maximum length of the two strings Example 1: 23 For two node labels “a b c” and “a b d e”, their similarity is: 2 = 0. 5 4

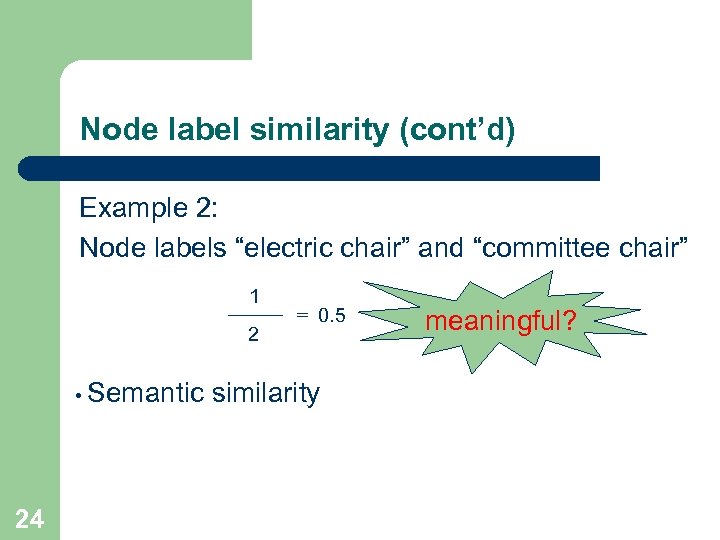Node label similarity (cont’d) Example 2: Node labels “electric chair” and “committee chair” 1 2 • Semantic 24 = 0. 5 similarity meaningful?

Node label similarity – inner nodes vs. leaf nodes l Inner nodes — class-oriented – – – l Leaf nodes — type-oriented – – 25 Inner node labels can be classes are located in a taxonomy tree taxonomic class similarity measures address, currency, date, price and so on type similarity measures (local similarity measures)

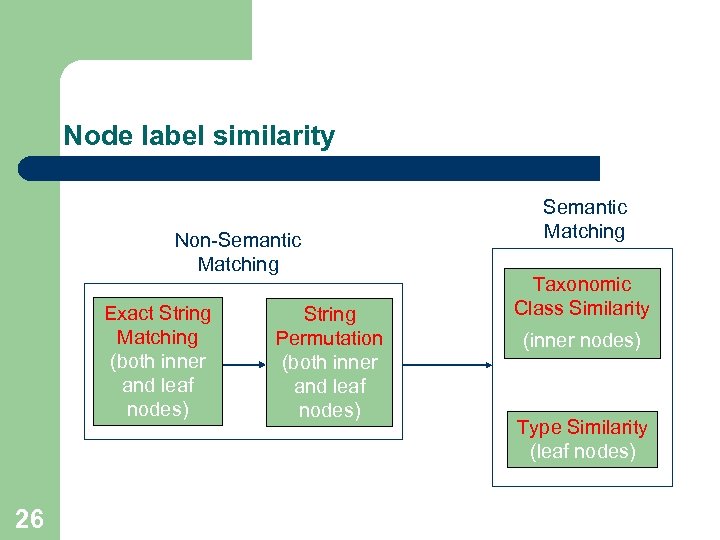Node label similarity Non-Semantic Matching Exact String Matching (both inner and leaf nodes) 26 String Permutation (both inner and leaf nodes) Semantic Matching Taxonomic Class Similarity (inner nodes) Type Similarity (leaf nodes)

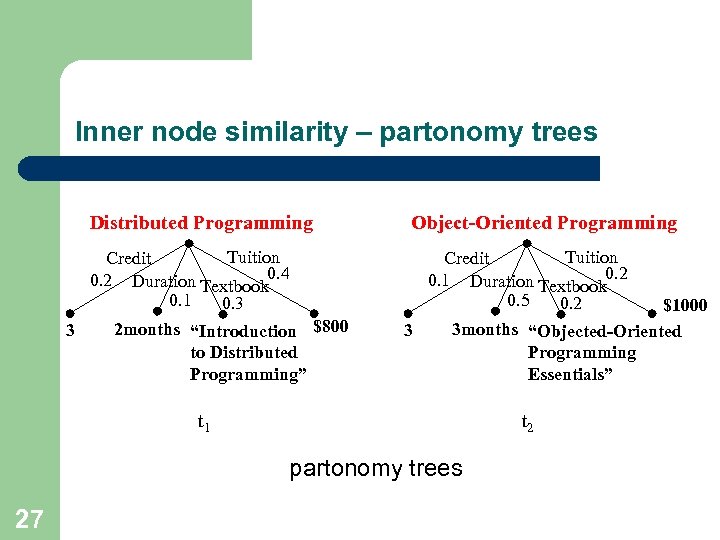Inner node similarity – partonomy trees Distributed Programming Tuition Credit 0. 2 Duration Textbook 0. 4 0. 1 0. 3 2 months “Introduction $800 3 to Distributed Programming” Object-Oriented Programming Tuition Credit 0. 1 Duration Textbook 0. 2 0. 5 0. 2 $1000 3 months “Objected-Oriented 3 Programming Essentials” t 1 t 2 partonomy trees 27

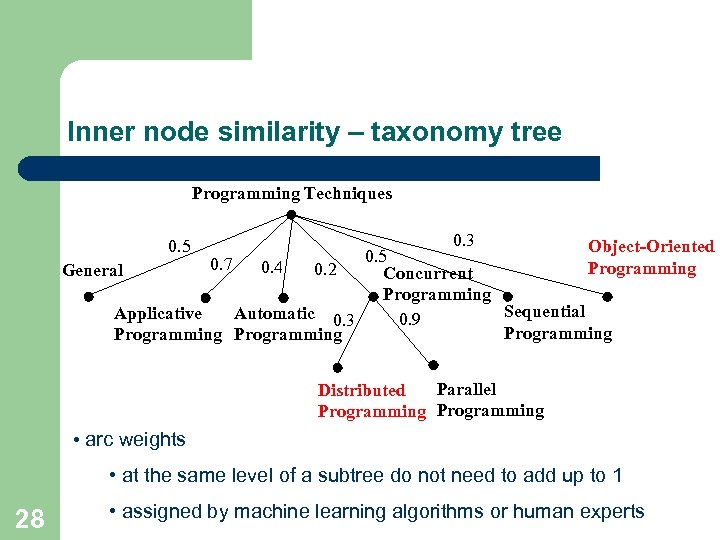Inner node similarity – taxonomy tree Programming Techniques 0. 5 0. 3 Object-Oriented 0. 5 0. 7 0. 4 Programming 0. 2 General Concurrent Programming Sequential Applicative Automatic 0. 3 0. 9 Programming Parallel Distributed Programming • arc weights • at the same level of a subtree do not need to add up to 1 28 • assigned by machine learning algorithms or human experts

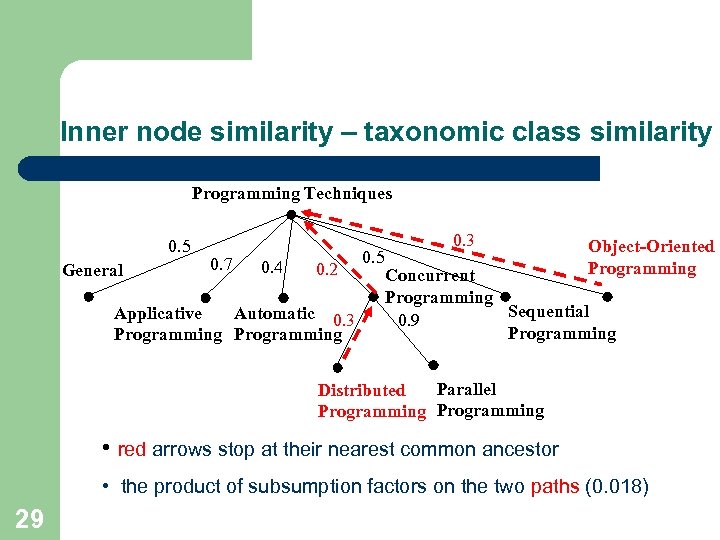Inner node similarity – taxonomic class similarity Programming Techniques 0. 5 General 0. 7 0. 4 0. 2 Applicative Automatic 0. 3 Programming 0. 5 0. 3 Object-Oriented Programming Concurrent Programming Sequential 0. 9 Programming Parallel Distributed Programming • red arrows stop at their nearest common ancestor • the product of subsumption factors on the two paths (0. 018) 29

Inner node similarity – separate to encoded taxonomy tree l Separate taxonomy tree – l How to compute semantic similarity without – – l l 30 extra taxonomic class similarity measures changing our partonomy similarity algorithm losing taxonomic semantic similarity Encode the (subsections) of taxonomy tree into partonomy trees Disjoint subsections of taxonomy lead to zero semantic similarity

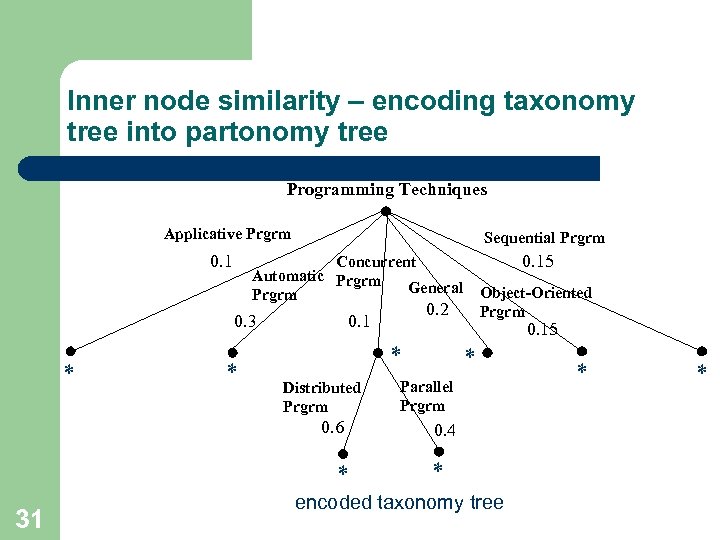Inner node similarity – encoding taxonomy tree into partonomy tree Programming Techniques Applicative Prgrm 0. 1 Sequential Prgrm 0. 3 * * 0. 15 * Distributed Prgrm * Object-Oriented Prgrm 0. 2 0. 1 0. 6 31 0. 15 Concurrent Automatic Prgrm General Prgrm * Parallel Prgrm 0. 4 * encoded taxonomy tree * *

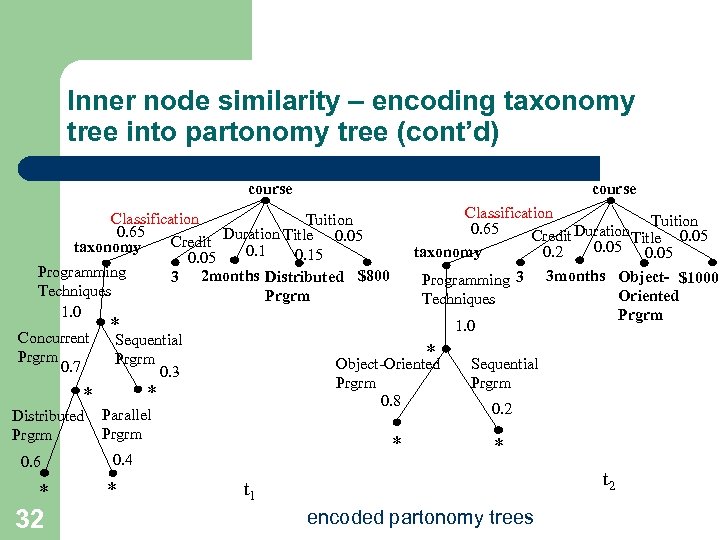Inner node similarity – encoding taxonomy tree into partonomy tree (cont’d) course Classification Tuition 0. 65 Duration Title 0. 05 Credit 0. 05 taxonomy 0. 2 Programming 3 3 months Object- $1000 Oriented Techniques Prgrm 1. 0 Classification Tuition 0. 65 Duration Title 0. 05 Credit taxonomy 0. 15 0. 05 Programming 3 2 months Distributed $800 Techniques Prgrm 1. 0 Concurrent Prgrm 0. 7 * Sequential Prgrm 0. 3 * * Distributed Prgrm 0. 6 * 32 * Object-Oriented Prgrm 0. 8 Parallel Prgrm * 0. 4 * Sequential Prgrm 0. 2 * t 2 t 1 encoded partonomy trees

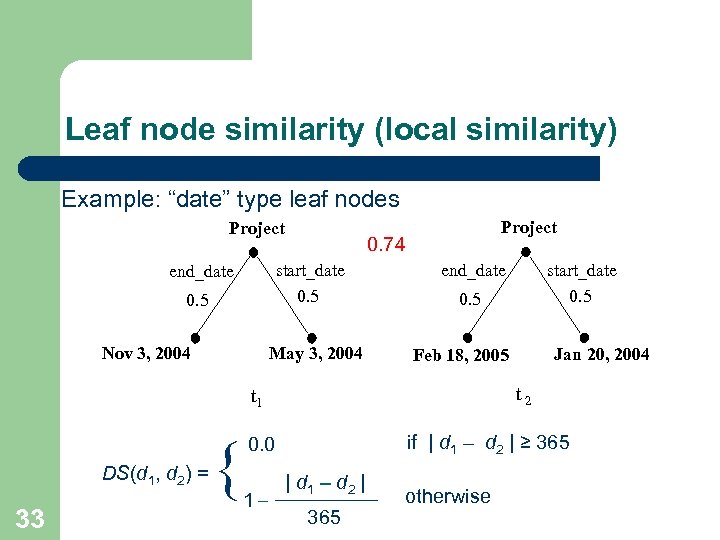Leaf node similarity (local similarity) Example: “date” type leaf nodes Project 0. 74 start_date 0. 5 end_date 0. 5 Nov 3, 2004 Project May 3, 2004 0. 5 33 { t 2 if | d 1 – d 2 | ≥ 365 0. 0 1– Jan 20, 2004 Feb 18, 2005 t 1 DS(d 1, d 2) = start_date 0. 5 end_date | d 1 – d 2 | 365 otherwise

Implementation l Relfun version – – l Java version – – – 34 exact string matching don’t care string permutation encoded taxonomy tree in partonomy tree (Teclantic) “date” type similarity measure

Conclusion l l l 35 Arc-labeled and arc-weighted trees Partonomy similarity algorithm – Traverses trees top-down – Computes similarity bottom-up Node label similarity – Exact string matching (both inner and leaf nodes) – String permutation (both inner and leaf nodes) – Taxonomic class similarity (only inner nodes) ü Taxonomy tree ü Encoding taxonomy tree into partonomy tree – Type similarity (only leaf nodes) ü “date” type similarity measures

Questions? 36