Weighing Evidence in the Absence of a Gold

Weighing Evidence in the Absence of a Gold Standard Phil Long Genome Institute of Singapore (joint work with K. R. K. “Krish” Murthy, Vinsensius Vega, Nir Friedman and Edison Liu. )

Problem: Ortholog mapping • • Pair genes in one organism with their equivalent counterparts in another Useful for supporting medical research using animal models

A little molecular biology • DNA has nucleotides (A, C, T and G) arranged linearly along chromosomes • Regions of DNA, called genes, encode proteins • Proteins biochemical workhorses • Proteins made up of amino acids • also strung together linearly • fold up to form 3 D structure

Mutations and evolution • Speciation often roughly as follows: • one species separated into two populations • separate populations’ genomes drift apart through mutation • important parts (e. g. genes) drift less • Orthologs have common evolutionary ancestor • Genes sometimes copied • • • original retains function copy drifts or dies out Both fine-grained and coarse-grained mutations

Evidence of orthology • (protein) sequence similarity • comparison with third organism • conservation of synteny. . .

Conserved synteny • Neighbor relationships often preserved • Consequently, similarity among their neighbors evidence that a pair of genes are orthologs

Plan • Identify numerical features corresponding to • • common similarity to third organism • • sequence similarity conservation of synteny “Learn” mapping from feature values to prediction

Problem – no “gold standard” • • for mouse-human orthology, Jackson database reasonable for human-zebrafish? human-pombe?

Another “no gold standard” problem: protein-protein interactions • Sources of evidence: • Yeast two-hybrid • Rosetta Stone • Phage display . . . • All yield errors

Related Theoretical Work [MV 95] – Problem • Goal: • • • given m training examples generated as below output accurate classifier h Training example generation: • All variables {0, 1}-valued • Y chosen randomly, fixed • X 1, . . . , Xn chosen independently with Pr(Xi = Y) = pi, where pi is • • • unknown, same when Y is 0 or 1 (crucial for analysis) only X 1, . . . , Xn given to training algorithm

Related Theoretical Work [MV 95] – Results • If n ≥ 3, can approach Bayes error (best possible for source) as m gets large • Idea: • variable “good” if often agrees with others • can e. g. solve for Pr(X 1 = Y) as function of Pr(X 1 = X 2), Pr(X 1 = X 3), and Pr(X 2 = X 3) • can estimate Pr(X 1 = X 2), Pr(X 1 = X 3), and Pr(X 2 = X 3) from the training data • can plug in to get estimates of Pr(X 1 = Y), . . . , Pr(Xn = Y) • can use resulting estimates of Pr(X 1 = Y), . . . , Pr(Xn = Y) to approximate optimal classifier for source

In our problem(s). . . • Pr(Y = 1) small • X 1, . . . , Xn continuous-valued • Reasonable to assume X 1, . . . , Xn conditionally independent given Y • Reasonable to assume Pr(Y = 1 | Xi = x) increasing in x, for all i • Sufficient to sort training examples in order of associated conditional probabilities that Y = 1

Key Idea • • Suppose Pr(Y = 1) known For variable i, - - - • • • Ui = 0 Ui = 1 - - - - - + -- - - + + + Set threshold so that Pr(Ui = 1) = Pr(Y = 1) Then Pr(Y = 1 and Ui = 0) = Pr(Y = 0 and Ui = 1) Can solve for these error probabilities for all i in terms of probabilities Ui’s agree, . . .

Final Plan (informal) • Assume various values of Pr(Y = 1); predict orthologs given each • For pairs of genes predicted to be orthologs even when Pr(Y = 1) assumed small, confidently predict orthology • For pairs of genes predicted to be orthologs only when Pr(Y = 1) assumed pretty big, predict orthology more tentatively

Final Plan – Probabilistic Viewpoint • Consider hidden variable Z: • • • takes values uniformly distributed in [0, 1] interpretation: “obviously orthologous” Assumptions • • • Pr(Y = 1| Z = z) increasing in z For all z, Pr(Z ≥ z | Xi = x ) increasing in x For various z • • • Let Vz = 1 if Z ≥ z, Vz = 0 otherwise Let Uz, i = 1 if Xi ≥ θz, i, Uz, i = 0 otherwise, where θz, i chosen so that Pr(Uz, i = 1) = Pr(Vz = 1) Interpretations: • Vz is “In the top 100(1 -z)% most likely to have Y = 1 overall” • Uz, i “In the top 100(1 -z) % most likely to have Y = 1 given Xi”

Final Plan - Algorithm • • Estimate conditional probability that Vz = 1, i. e. that Z ≥ z, given each training example, using estimated probabilities pairs of Uz, i’s agree Add to estimate Z’s; sort by estimates.

Practical problem • Small errors in estimates of Pr(Uz, i = Uz, j)’s can lead to large errors in estimates of Pr(Uz, i = Vz )’s (in fact, program crashes). • Solution: • when Pr(Vz = 1) small is important case (confident predictions) • can approximate: Pr(Uz, i ≠ Vz ) ~ ½ (Pr(Uz, i ≠ Uz, j) + Pr(Uz, i ≠ Uz, k) - Pr(Uz, j ≠ Uz, k)).

Evaluation: Artificial Source • Examples generated using randomly chosen probability distribution: • • Pr(Yz = 1) = 0. 1, n = 5 For each i, • • choose μi uniformly from [min, max] set distributions for ith variable: • • Pr(Xi | Y=0) = N(-μi, 1), Pr(Xi | Y=1) = N(μi, 1). Evaluate using area under the ROC curve Repeat 100 times, average

ROC curve 1 Area under the ROC curve True positives False positives 1

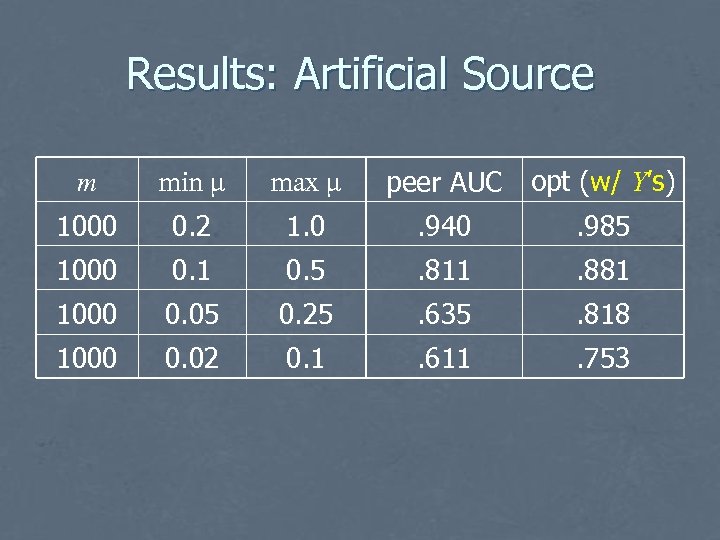
Results: Artificial Source m min μ max μ peer AUC opt (w/ Y’s) 1000 0. 2 1. 0 . 940 . 985 1000 0. 1 0. 5 . 811 . 881 1000 0. 05 0. 25 . 635 . 818 1000 0. 02 0. 1 . 611 . 753

Evaluation: mouse-human ortholog mapping • • • Use Jackson mouse-human ortholog database as “gold standard” Apply algorithm, post-processing to map each gene to unique ortholog Compare with analogous BLAST-only algorithm Plot ROC curve Treat anything not in database as non-ortholog • • some “false positives” in fact correct error rate overestimated

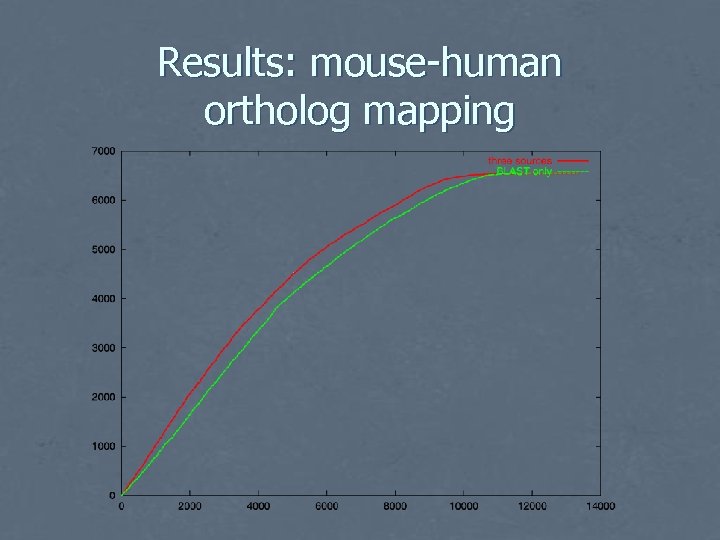
Results: mouse-human ortholog mapping

Open problems • Given our assumptions, is there an algorithm for learning using random examples that always approaches the optimal AUC given knowledge of the source? • Is discretizing the independent variables necessary? • How does our method compare with other natural algorithms? (E. g. what about algorithms based on clustering? )