Week 6 Model selection Overview Questions from last

Week 6: Model selection Overview Questions from last week Model selection in multivariable analysis -bivariate significance -interaction and confounding Discussion of the 3 articles Data analysis discussion

Univariate, bivariate, and multivariate analysis: a review Type of analysis Type of variable/test used Purpose Univariate Continuous: mean, median, standard deviation Histogram Outcome variable: to assess normal distribution Exposure variable: to examine distribution, missing variables, etc. Univariate Categorical: Outcome variable: to Frequency distribution assess frequency Exposure variables: to assess frequency (are there enough observations in each category? ), missing variables

Univariate, bivariate, and multivariate analysis: a review Type of analysis Type of variable/test used Purpose Bivariate: for exposure groups Continuous: t-test between exposure groups Categorical: Chi-square test To assess differences between groups prior to analysis To look for possible confounding relationships. Bivariate for outcome groups Continuous: t-test Categorical: Odds ratio To look for significant differences in the outcome variable by exposure variables ‘Crude’ analysis

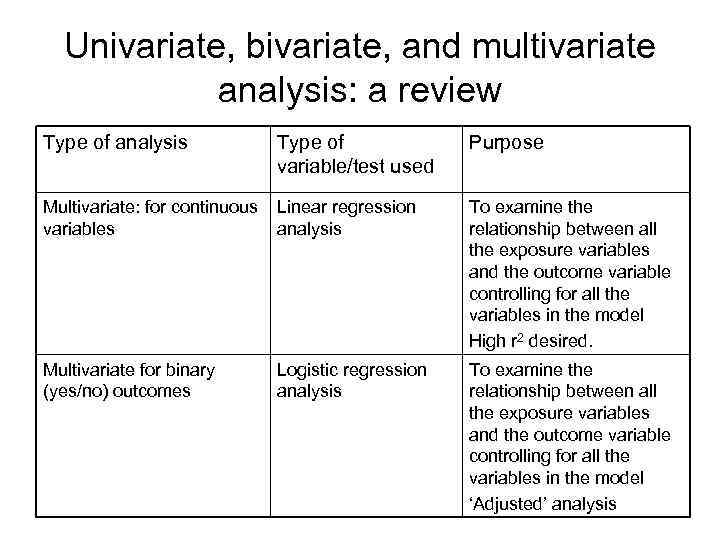Univariate, bivariate, and multivariate analysis: a review Type of analysis Type of variable/test used Purpose Multivariate: for continuous variables Linear regression analysis To examine the relationship between all the exposure variables and the outcome variable controlling for all the variables in the model High r 2 desired. Multivariate for binary (yes/no) outcomes Logistic regression analysis To examine the relationship between all the exposure variables and the outcome variable controlling for all the variables in the model ‘Adjusted’ analysis

Back to the mathematical model • In linear regression Y’ (known as Y prime) is the predicted value on the outcome variable • A is the Y axis intercept • β 1 is the coefficient assigned through regression • X 1 is the unit of the exposure variable • For logistic regression the model is: • ln • ( Y’ 1 -Y’ ) =A + β 1 X 1 + β 2 X 2 + β 3 X 3

Model selection • A ‘full’ model is one that includes all the variables • A ‘null’ model is one that includes only the intercept • Selection of which variables to include can be done by you, by the computer, or both • Types of selection: • Forward, backward, stepwise

Backward selection • Starts with a full model • Removes variables starting with the least significant variable • Often the best approach to start with

• What do you get when you cross a statistician with a chiropractor? • You get an adjusted R squared from a BACKward regression problem!

Forward selection • Starts with a null model • Enters the variables into the model starting with the most significant • Can miss important associations or interactions

Stepwise selection • Starts with a full or null model (usually a full model or backwards stepwise) • Adds or removes variables based on their significance in the model • Looks at variable itself and the relationship with other in the model • Can be considered the best automatic model selection especially with many exposure variables

Maximum likelihood model fitting • Most logistic regression models use the maximum likelihood model to fit regression models • The log-likelihood is calculated based on predicted and actual outcomes A good model has a NON-significant LL • A goodness-of-fit chi-square is calculated (usually compares a constant-only model to the one you created) -2 LL in null model - -2 LL in your model with df = number of exposure variable • A good model has a significant goodness of fit

Linear regression model fitting • Uses the same principles as logistic regression • Often starts with a full model • You need to examine 2 things: -the r 2 and adjusted r 2 -changes in significance of each variable as the model changes • The goal is to achieve the model with the highest adjusted r 2

Confounding and effect modification • Confounding is classified as a variable that is associated with the exposure variable and the outcome variable, but is not on the causal pathway • E. g. smoking can be a confounding variable in the relationship between drinking alcohol and oral cancer • Effect modification is when the variable has a different effect in subgroups of the population • E. g. , the effectiveness of a form to reduce medication errors can depend on whether the form is for home or the ED • These need to be considered when fitting a regression model

For next week • Read articles • Start modelling your own data using the appropriate multivariable technique • Think about model selection, interactions and possibility of confounding