370bed7a073b537d3656813d522f7eb7.ppt
- Количество слайдов: 20

Wave turbulence in resonators Elena Kartashova, RISC 18. 10. 07, Physical Colloquium 1

Main goals of this talk • To put wave trubulence theory into the general physical context • To show math. difficulties and give an idea of the solution methods • To demostrate how to use the results to describe a real physical phenomenon 2
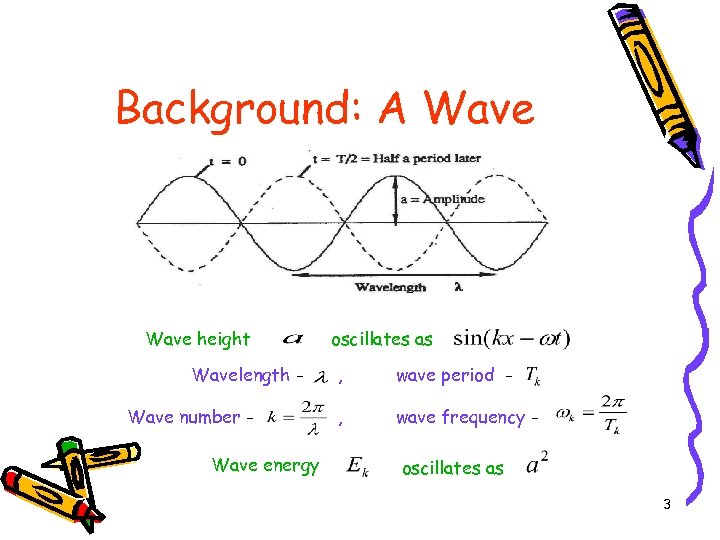
Background: A Wave height Wavelength Wave number Wave energy oscillates as , wave period - , wave frequency oscillates as 3

Resonator – finite-size system LINEAR 1 D-WAVE violin string or organ pipe is a length of the string, is arbitrary integer. Different initial conditions: initial frequency - half a period (pure tone, one Fourier harmonic) • energy concentrated in ONE WAVE initial frequency - arbitrary (overtones, all Fourier harmonics) • energy distributed among ALL THE WAVES 4

Enrico Fermi (1901 -1954) NONLINEAR 1 D-STRING 1938 Nobel Prise (nuclear reaction) 1953 Numerical computations on MANIAC, with Pasta & Ulam 1955 Publication of FPU problem 5

Fermi-Pasta-Ulam problem Number of harmonics for numerical simulations: n=32, 64 6

Numerical results Expectations due to the Boltzmann theorem: evolution of the INFINITE system from arbitrary initial conditions yields equipartitioned distribution of energy among the waves. Results: one wave decays into two waves which satisfy time and space synchronization conditions (resonance conditions) and the wave system demonstrates almost exactly periodic behavior: energy goes into other waves and after some time it COMES BACK into the first wave. 7

Two possible scenarios why the Bolzmann theorem does not work • Closeness to an integrable system • Discretness of eigen-modes in bounded resonators FPU is not resolved till now. One of the reasons is degeneracy of conservation laws due to 1 D and linear dispersion law. On the other side, there are many physically interesting 2 D waves in bounded domains with no degeneracy of conservation laws. 8

Nonlinear waves in 2 Dmedia 2 D-waves propagate in two directions height of the wave oscillates as Now we have • wave vector (not wave number) • in resonators are integers • dispersion function is 9

Examples • 1. Capillary waves (due to surface tension): 1. • 2. Water gravity surface waves (due to gravity acceleration): 2. • 3. Oceanic planetary waves (due to the Earth rotation), called also Rossby waves: 10

Rossby Waves in the Earth Atmosphere RW detach the masses of cold/warm air that become cyclones and anticyclones and are responsible for day-today weather patterns. Radar image of a tropical cyclone. 11

Physical scales when discreteness is important? • Capillary waves: < 4 cm (desktop experiments) • Water gravity waves: ~ 0. 1 - 1000 m (laboratory experiments, Chanels, Bays, Seas) • Oceanic Rossby waves: • Atmospheric Rossby waves: Atm. ) Main message: ~ 100 -200 km (Oceans) ~ 1000 -5000 km (Earth is important! 12

Main result Discrete resonances DO exist in many physically relevant 2 D-wave systems! What was the problem? Left part has no roots, right part still have them, After taking 8 times power 2, we get terms of commulative degree 16 and some roots are still left. Already at this step, for wave numbers ~ 1000, we need to make computations with integers of order. 13

Powerful trick Last equation is a special case of the Fermat’s Last theorem proven by Euler for n=3. RESULTS: 1. Math: the problem is equivalent to the Fermat‘s Last theorem 2. Phys: capillary waves do not have 3 -wave resonances in a rectangular box 3. Comp: computation time reduced from weeks to 5 -15 minutes 14 (for dozens of physically relevant dispersion functions)
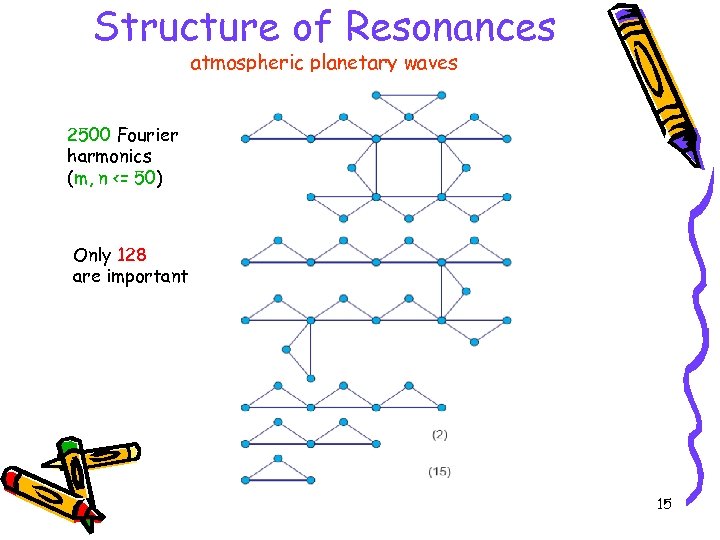
Structure of Resonances atmospheric planetary waves 2500 Fourier harmonics (m, n <= 50) Only 128 are important 15

Important remark • To applicate this reasoning to a real physical problem we have answer the question about quasi-resonances: is called resonance width and corresponds to the accuracy of laboratory experiments 16

Intra-seasonal oscillations in the Earth atmosphere nonlinear part The beauty of this example is due to 2 facts: 1. Dynamical system is solvable analytically 2. 10. 000 atmospheric measurements per day are available 17

Statistical Wave Turbulence (STW) • Kolmogorov 1941, 61 (locally homogeneous & isotropic, existence of an inertial interval -> power-law energy spectrum) • Hasselman 1962, Zakharov 1967 (wave kinetic equation ~ Bolzmann equation) • Kolmogorov 1961, Arnold 1961, Moser 1962 (KAMtheory: small divisor problem) • Zakharov, Shulman 1981 (KAM-theory for SWT ) • Zakharov, L’vov, Falkovich 1992 (strict mathematical theory of SWT, without discrete effects ) 18
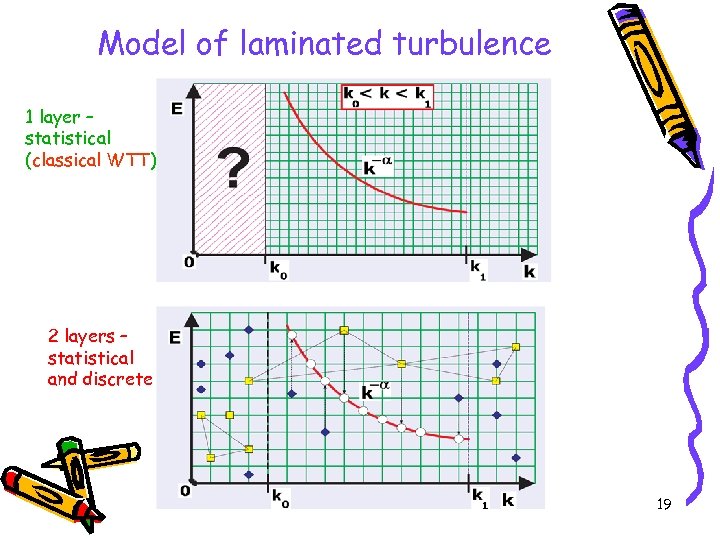
Model of laminated turbulence 1 layer – statistical (classical WTT) 2 layers – statistical and discrete 19

MAIN RESULTS • Existence of exact resonances is established for many physically relevant wave systems, computational methods are developed and implemented • Dynamics of a wave system in resonator is defined by a few independent wave clusters • Model of intra-seasonal oscillations in the Earth atmosphere is developed (important for weather and climate predictability) • Some more… Further studies are in PROGRESS (theoretical – with Weizmann Institute, Israel; experimental – with Warwick & Hull Universities, UK) 20
370bed7a073b537d3656813d522f7eb7.ppt