9295a3d30cf6ebe5e16b9f2a0ae98d21.ppt
- Количество слайдов: 16

Warwick Turbulence Symposium: Workshop "Environmental Turbulence from Clouds through the Ocean" March 13 -17, 2006 THEORETICAL AND EXPERIMENTAL MODELLING OF INTENSIVE ATMOSPHERIC VORTICES Galina Levina 1, 2 1 Institute of Continuous Media Mechanics UB RAS, Perm 2 Space Research Institute RAS, Moscow Financial support: Russian Foundation for Basic Research NN 03 -05 -64593, 04 -05 -64315 International Science and Technology Center, Project #2021 THE AIM OF THE INVESTIGATION: Theoretical, laboratory and numerical modelling is intended to study large-scale intensive vortices formation in the atmosphere and physical mechanisms involved in the cyclogenesis

OUTLINE: 1. Motivation 2. Large-scale α-like instabilities. 3. Turbulent vortex dynamo in convectively unstable fluid. 4. Theoretical model. Mean-field equations. 5. Numerical simulation of helical-vortex convection: - helical-vortex effects in Rayleigh-Bénard convection with large aspect ratio. 6. Parameterization of helical convective turbulence for numerical meteorological models. 7. A way to examine the hypothesis of turbulent vortex dynamo in simulation of tropical cyclogenesis. SUMMARY Experimental Modelling --- poster LARGE-SCALE SPIRAL VORTEX DRIVEN BY LOCAL HEATING IN A SLOWLY ROTATING TURBULENT FLUID G. P. Bogatyryov, V. G. Batalov, P. G. Frick, I. V. Kolesnichenko, G. V. Levina, and A. N. Sukhanovsky

Large-Scale Alpha-Like Instabilities in Turbulent Media Origin: Specific properties of small-scale turbulence displaying a symmetry break Examples: Helical Turbulence generated by pseudovector forces – magnetic, Coriolis force fields • Alpha-Effect in Magnetohydrodynamics – Steenbeck, Krause, and Rädler (1966) • Helical-Vortex Instability in non-MHD Hydrodynamics – Moiseev, Rutkevich, Sagdeev, Tur, Khomenko, and Yanovsky (1983 -1988) • Turbulent Vortex Dynamo in the Moist Atmosphere – Kurgansky (1998) Anisotropic Turbulence lacking parity-invariance – generated by a special forcing • Anisotropic Kinetic Alpha (AKA) Effect – illustrated by full simulation in 3 D Frisch, She, and Sulem (1987) Turbulent helicity evidence: The first measurements in the atmospheric boundary layer – B. Koprov, V. Ponomarev, O. Chkhetiani (2005)

DRY VORTICES: VOLUMETRIC HEATING BY HOT SOLID PARTICLES TURBULENT VORTEX DYNAMO THEORY Gives a threshold for the large-scale vortex instability Results in suggesting the generation of positive feedback between the horizontal and vertical circulation Condition for non-zero dynamo-effect in a convectively unstable rotating fluid: volumetric heat release additionally to the heating from below Rutkevich (1993), Kurgansky (1998) MOIST VORTICES: VOLUMETRIC HEATING BY LATENT HEAT RELEASE

TURBULENT VORTEX DYNAMO IN CONVECTIVELY UNSTABLE FLUID MEAN-FIELD EQUATIONS Space Research Institute, Moscow: Moiseev et al. , Rutkevich (1983 -1993) C – characterizes the intensity of helical feedback and depends on rotation Ω and internal heat release intensity B, and characteristics of small-scale convective turbulence With the helical feedback introducing (C≠ 0) : • C-terms generate a new instability, • there exists a threshold of instability, • feedback enhancing results in the threshold decrease and • horizontal dimensions of convective structures increase

P. B. Rutkevich. Equation for vortex instability caused by convective turbulence and the Coriolis force (1993), JETP, v. 77, pp. 933 -938 Ω – background rotation, E - density of turbulence energy, λ, τ - the most energetic scale and characteristic time of the turbulent velocity correlation, A - constant temperature gradient between the horizontal boundaries, B - coefficient characterizing the power of internal heat sources, h - layer height, ν - molecular coefficient of kinematic viscosity, νT - coefficient of turbulent viscosity on the large scale, η - dimensionless parameter specifying the aspect ratio (of typical vertical to horizontal dimension) for small-scale convective structures.

NUMERICAL SIMULATION OF HELICAL-VORTEX CONVECTION Burylov, Firulyov, Levina Model force simulates the influence of small-scale helical turbulence generated by joint effect of the Coriolis force and internal heat release: is applied to developed convective flows • has the identical tensor structure with C-terms responsible for generation of new instability in the mean-field equation, • makes the flow helical, • generates a positive feedback between the poloidal and toroidal components of the velocity field. Linear Stability Analysis: helical force operates favouring the large scale flow generation and decreasing the threshold of instability

Boussinesq Convection with Helical Force The helical force: • works and can pump an additional energy, • z-component is a necessary element to close the feedback loop between the horizontal and vertical circulation in a forming vortex structure • Laminar Rayleigh-Bénard convection produces a great number of similar convective cells that can be considered as structures of an intermediate scale. • Helical force pumping the energy into the system simulates the influence of small-scale helical turbulence. An intriguing idea arises: is it possible to simulate any signs of large-scale instability in these relatively simple conditions ?

Energy and Helicity Balance in Helical-Vortex Convection Helical force operates contributing to both energy and helicity balances. Numerical analysis is the most effective way to give quantitative estimations for different terms in balance equations.

Helical-Vortex Effects in Laminar Convection 3 D Laminar Rayleigh-Bénard convection, AR = 10 - Boussinesq equations with model force - Finite differences. Explicit scheme. Computational domain R R=10 H z z H (r, , z) Initial distribution r N r N z = 200 60 r Stationary convection at S=0 BOUNDARY CONDITIONS Impenetrable, rigid, no-slip T Heating from below, lateral surface is adiabatic PHYSICAL FIELDS Temperature, azimuthal velocity, vorticity, stream function
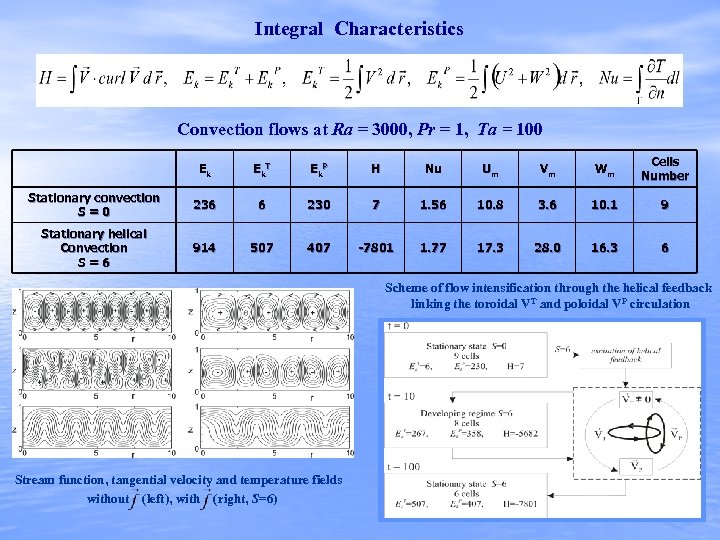
Integral Characteristics Convection flows at Ra = 3000, Pr = 1, Ta = 100 Ek Ek. T Ek. P H Nu Um Vm Wm Cells Number Stationary convection S=0 236 6 230 7 1. 56 10. 8 3. 6 10. 1 9 Stationary helical Convection S=6 914 507 407 -7801 1. 77 17. 3 28. 0 16. 3 6 Scheme of flow intensification through the helical feedback linking the toroidal VT and poloidal VP circulation Stream function, tangential velocity and temperature fields without (left), with (right, S=6)

Cells Merging Stream function field: S=6. 5, Ra=1100

- the booklet summarizes results on proposed numerical approach for simulating the large-scale helical-vortex instability in rotating Boussinesq convection with internal heat sources OPINIONS ABOUT GEOPHYSICAL APPLICATIONS: Alexander Khain (University of Jerusalem, Israel), April 2005: “You have to make other people who are in Tropical Cyclone modeling be interested. This effect may have a potential importance for the problem of development of tropical depressions. ” Kerry Emanuel (MIT, USA), April 2005: “I think your work has great potential applicability to dust devils. While this may seem like a trivial phenomenon, it is proving to be quite otherwise on Mars. ” NEXT STEPS: • DNS with/without the helical force for Boussinesq convection • Examination of helical-vortex effects in tropical cyclogenesis - with/without the helical force to parameterize the helical features of convective atmospheric turbulence in numerical meteorological models.

PARAMETERIZATION OF HELICAL CONVECTIVE TURBULENCE TO INCLUDE IN NUMERICAL METEOROLOGICAL MODELS Ω – background rotation, E - density of turbulence energy, λ, τ - the most energetic scale and characteristic time of the turbulent velocity correlation, A - constant temperature gradient between the horizontal boundaries, B - coefficient characterizing the power of internal heat sources, h - layer height, ν - molecular coefficient of kinematic viscosity, νT - coefficient of turbulent viscosity on the large scale, η - dimensionless parameter specifying the aspect ratio (of typical vertical to horizontal dimension) for small-scale convective structures. Ω = 10 -4 s-1 , Е = 102 m 2/s 2 , λ = 103 m, τ = 103 s, А = 10 -2 K/m, h = 104 m, ν = 10 -5 m 2/s, νT = 102 -103 m 2/s, 2 = 10, C 101 -102 B

A WAY TO EXAMINE THE HYPOTHESIS OF TURBULENT VORTEX DYNAMO IN MODELLING OF TROPICAL CYCLOGENESIS Examining the helical-vortex effects at initial stages of tropical cyclone evolution may result in a finding of threshold for the large-scale vortex instability Research Program proposed within a visit to Colorado State University (Fort Collins, February, 2006): • concept of vortical hot tower (VHT) route to tropical cyclogenesis of M. T. Montgomery et al. (2006), JAS, – represents the most appropriate basis to take into account helical features of convective atmospheric turbulence; • numerical realization - non-hydrostatic mesoscale models -- MM 5, RAMS; - near-cloud-resolving simulation, 2 -3 km horizontal grid spacing; - applying both DNS and proposed parameterization, - meteorological database on TC observation and investigation. Visiting Scientist Program – N 00014 -06 -1 -4011

SUMMARY I. With applying the helical force to the Boussinesq convection 1. The existence of threshold for large-scale instability has been shown. 2. New effects have been found: - non-zero helicity generation, - flow intensification through the positive feedback loop between the horizontal and vertical circulation, - merging of helical vortex cells, - intensification and qualitative change in heat transfer. Explanation is given how the energy of the additional helical source can be effectively converted into the energy of intensive large-scale vortex flow. 3. Some features of tropical cyclone can be simulated: - generation of intensive tangential velocity field, - enlargement of horizontal structure scale by cells merging. II. Parameterization of helical features of convective atmospheric turbulence and way to examine the hypothesis of turbulent vortex dynamo in simulation of tropical cyclogenesis have been proposed.
9295a3d30cf6ebe5e16b9f2a0ae98d21.ppt