Warm Up Sketch the graph of each function

Warm Up Sketch the graph of each function and evaluate both for x=2 (a) y=2 x (b) y=(½)x

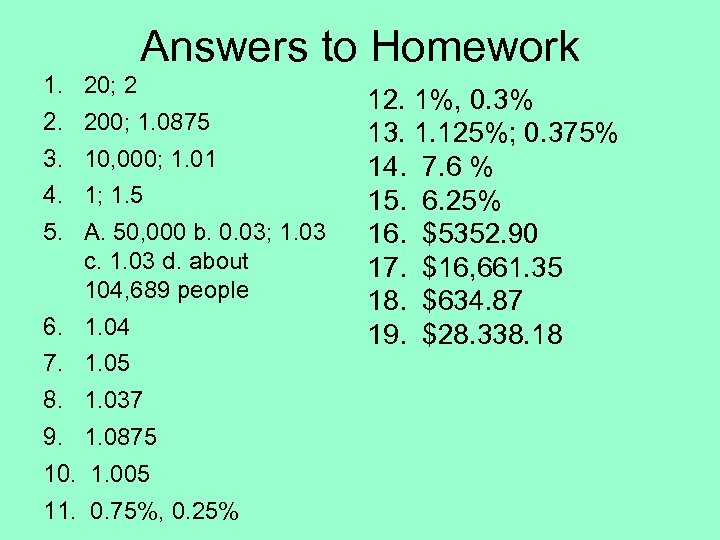Answers to Homework 1. 20; 2 2. 200; 1. 0875 3. 10, 000; 1. 01 4. 1; 1. 5 5. A. 50, 000 b. 0. 03; 1. 03 c. 1. 03 d. about 104, 689 people 6. 1. 04 7. 1. 05 8. 1. 037 9. 1. 0875 10. 1. 005 11. 0. 75%, 0. 25% 12. 1%, 0. 3% 13. 1. 125%; 0. 375% 14. 7. 6 % 15. 6. 25% 16. $5352. 90 17. $16, 661. 35 18. $634. 87 19. $28. 338. 18

February 12, 2010 8 -8 Exponential Growth and Decay Objective: Model and solve problems involving exponential growth and decay.

Quiz on 8. 7

Rate of exponential decay – The percent decrease r in the equation y = a(1 – r)t. Rate of exponential growth – The percent increase r in the equation y = a(1 + r)t. (a is the initial amount, r is percent, and t is time in which percent is calculated)

1. Suppose you want to buy a used car that costs $11, 800. The expected depreciation of the car is 20% per year. Estimate the depreciated value of the car after 6 years.

2. An investment of $75, 000 increases at a rate of 12. 5% per year. Find the value o the investment after 30 yr.

3. The bear population increases at a rate of 2% per year. There are 1573 bears this year. Write a function that models the bear population. How many bears will there be in 10 yr?

If an amount of money, P, called the principal, is invested at a rate of r, compounded n periods per year, then the amount of money after t years is given by

Continuous compounding of interest is given by

Examples: 1. Compare the amount after 5 years when $1000 is invested in each type of account. A. 10% compounded monthly

B. 9. 9% compounded weekly C. 9. 9% compounded continuously

2. How much money needs to be invested in an account paying 7. 8% compounded monthly, so that a person will have $5000 in 5 years?

Important Things to Remember: 1. If b>1, we identify the function as growth. If b<1, we identify the function as decay. 2. a is the initial amount 3. b is the growth factor 4. 1 -b is the % of increase or decrease

Classwork: WB p. 110 #1 -3 Homework: p. 441 1 -19