WARM UP FRI SEPT TH 6 EXAM

WARM UP FRI SEPT TH 6 EXAM – 1 Measurement-Math-Lab Skills READ TEXT (pgs. 32 -37) re: Motion

UNIT 2 A LINEAR MOTION

Unit 2 A: Linear Motion You can describe the motion of an object by its: distance | speed | direction acceleration

DAILY WARM UP • Is motion relative? • Does it depend on your perspective?

2. 1 Motion Is Relative How do you know if an object is moving? • Is your book moving? The book is at rest, relative to the table, BUT It’s moving at about 30 km/s relative to the sun. An object is moving if its position relative to a fixed point is changing.

2. 1 Motion Is Relative An object’s motion must be described relative to something else. • shuttle 8 km/s relative to Earth below • race car 300 km/h relative to the track • The speeds of things on Earth are usually measured relative to the Earth’s surface.

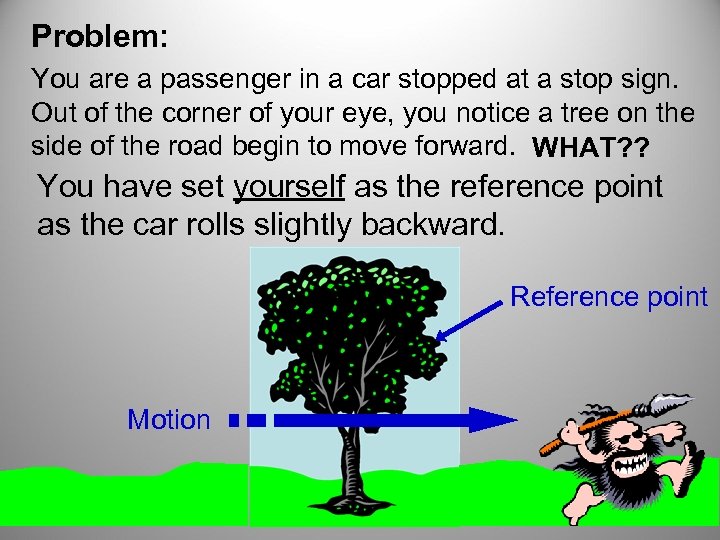Problem: You are a passenger in a car stopped at a stop sign. Out of the corner of your eye, you notice a tree on the side of the road begin to move forward. WHAT? ? You have set yourself as the reference point as the car rolls slightly backward. Reference point Motion

MIKE’S PHYSICS Video

Methods of Motion Honors Physics

The bottom line…. Motion is RELATIVE It depends completely on how you want to look at the moving object. You establish a frame of reference! Example: You are sitting in an airplane which is moving at a speed of 100 km/h and there is a fly sitting on your head. (a) What is your speed relative to the ground? (b) What is your speed relative to the seat you're sitting it? 100 km/hr (c) What is the speed of the fly relative to you? 0 km/hr

Displacement (x or y) "Change in position" It is not necessarily the total distance traveled. In fact, displacement and distance are entirely different concepts. Displacement is relative to an axis. o o o "x" displacement means you are moving horizontally either right or left. "y" displacement means you are moving vertically either up or down. The word change is expressed using the Greek letter DELTA ( Δ ). To find the change you ALWAYS subtract your FINAL - INITIAL position It is therefore expressed as either Δx = xf - xi or Δy = yf - yi Distance - How far you travel regardless of direction.

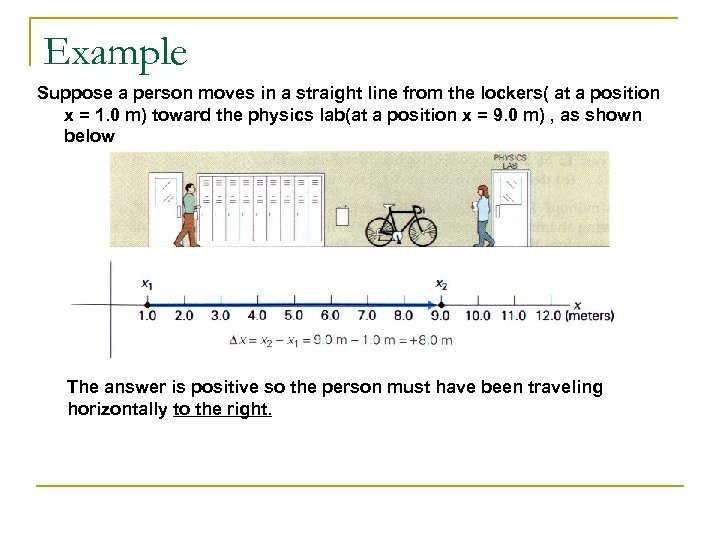Example Suppose a person moves in a straight line from the lockers( at a position x = 1. 0 m) toward the physics lab(at a position x = 9. 0 m) , as shown below The answer is positive so the person must have been traveling horizontally to the right.

Example Suppose the person turns around! The answer is negative so the person must have been traveling horizontally to the left What is the DISPLACEMENT for the entire trip? What is the total DISTANCE for the entire trip?

Average Velocity is defined as: “The RATE at which DISPLACEMENT changes”. Rate = ANY quantity divided by TIME. Average SPEED is simply the “RATE at which DISTANCE changes”.

Example A quarterback throws a pass to a defender on the other team who intercepts the football. Assume the defender had to run 50 m away from the quarterback to catch the ball, then 15 m towards the quarterback before he is tackled. The entire play took 8 seconds. Let's look at the defender's average velocity: Let's look at the defender's speed: “m/s” is the derived unit for both speed and velocity.

Slope – A basic graph model A basic model for understanding graphs in physics is SLOPE. Using the model - Look at the formula for velocity. Who gets to play the role of the slope? Velocity Who gets to play the role of the y-axis or the rise? Displacement Who get to play the role of the x-axis or the run? Time What does all the mean? It means that if your are given a Displacement vs. Time graph, to find the velocity of an object during specific time intervals simply find the slope.

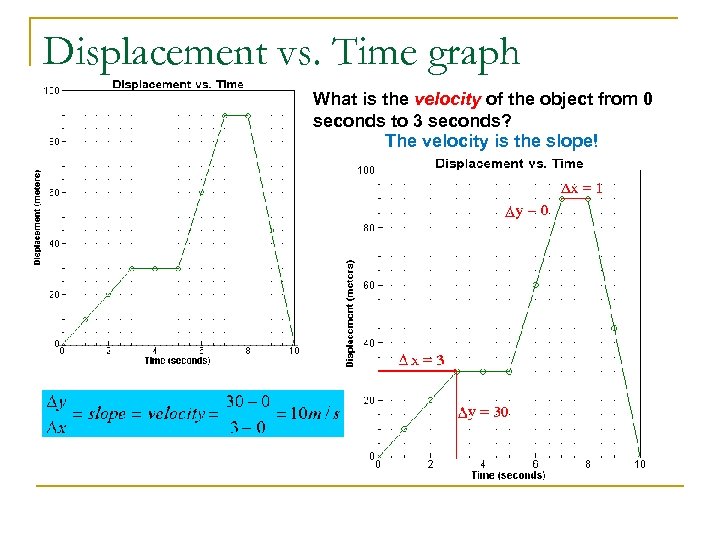Displacement vs. Time graph What is the velocity of the object from 0 seconds to 3 seconds? The velocity is the slope!

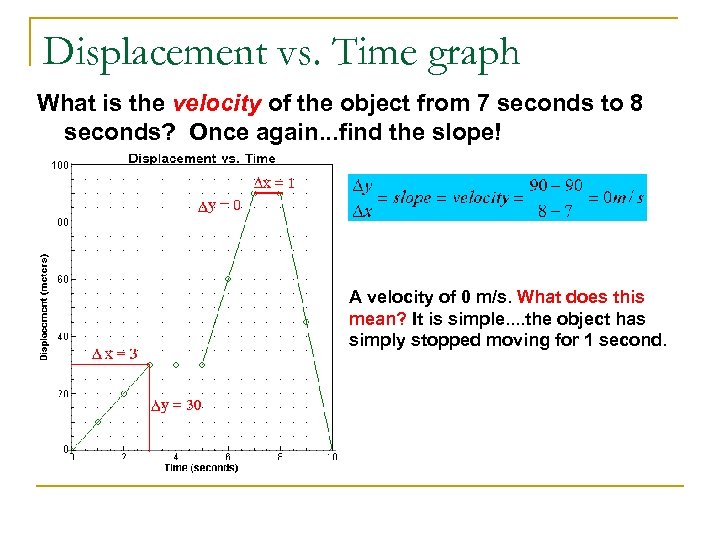Displacement vs. Time graph What is the velocity of the object from 7 seconds to 8 seconds? Once again. . . find the slope! A velocity of 0 m/s. What does this mean? It is simple. . the object has simply stopped moving for 1 second.

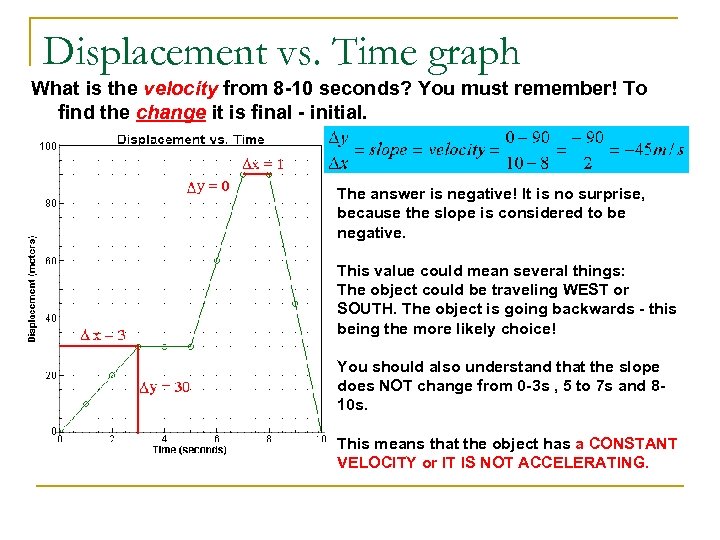Displacement vs. Time graph What is the velocity from 8 -10 seconds? You must remember! To find the change it is final - initial. The answer is negative! It is no surprise, because the slope is considered to be negative. This value could mean several things: The object could be traveling WEST or SOUTH. The object is going backwards - this being the more likely choice! You should also understand that the slope does NOT change from 0 -3 s , 5 to 7 s and 8 - 10 s. This means that the object has a CONSTANT VELOCITY or IT IS NOT ACCELERATING.

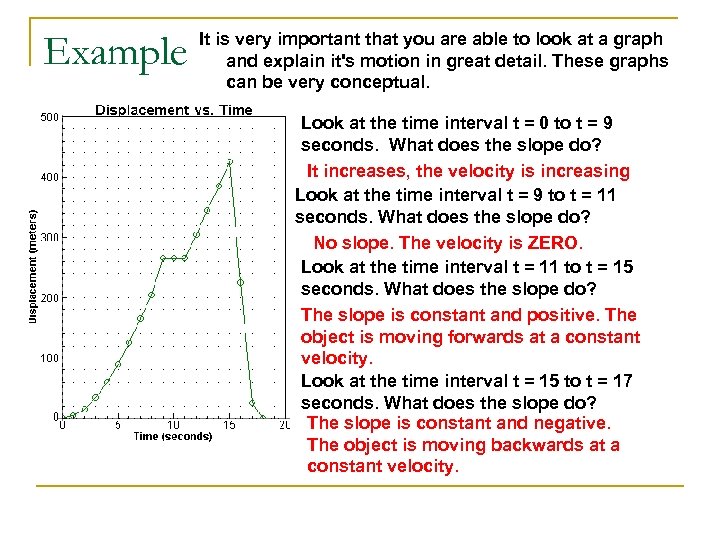Example It is very important that you are able to look at a graph and explain it's motion in great detail. These graphs can be very conceptual. Look at the time interval t = 0 to t = 9 seconds. What does the slope do? It increases, the velocity is increasing Look at the time interval t = 9 to t = 11 seconds. What does the slope do? No slope. The velocity is ZERO. Look at the time interval t = 11 to t = 15 seconds. What does the slope do? The slope is constant and positive. The object is moving forwards at a constant velocity. Look at the time interval t = 15 to t = 17 seconds. What does the slope do? The slope is constant and negative. The object is moving backwards at a constant velocity.

2. 2 Speed 400 yrs ago, people described motion as simply “slow” or “fast. ” Galileo was the first to measure speed by the distance covered and the time it takes. distance speed = time 5 mi avg. speed = 0. 20 h avg. speed = 25 mi/h

2. 2 Speed

2. 2 Speed Instantaneous Speed Cars do not always move at a constant speed. You can tell the speed of the car at any instant by looking at the car’s speedometer. instantaneous speed: the speed at any instant average speed: total distance time

2. 2 Speed If we know average speed and travel time, the distance traveled is easy to find. distance speed = time distance = speed x time Example: If your average speed is 80 km/h on a 4 -hour trip, then how far did you travel? distance = 80 km = x km 1 h 4 hr 320 km

2. 2 Speed If a cheetah can maintain a constant speed of 25 m/s, it will cover 25 meters every second. At this rate, how far will it travel in 10 seconds? distance = (25 m) = (x m) = (1 s) 10 s 250 m distance = speed x time In 1 minute? distance = (25 m) x (x m) = (1 s) (60 s) 1500 m

2. 2 Speed The speedometer in every car also has an odometer that records the distance traveled. If the odometer reads zero at the beginning of a trip and 35 km a half hour later, what is the average speed? distance 35 km speed = = time 0. 5 h = 70 km/h

Quick Quiz! 1. Jake walks east through a passenger car on a train that moves 10 m/s in the same direction. Jake’s speed relative to the car is 2 m/s. Jake’s speed relative to an observer at rest outside the train is ___. A. 2 m/s B. 5 m/s C. 8 m/s D. 12 m/s 2. 1

Quick Quiz. 2. A gazelle travels 2 km in a half hour. The gazelle’s average speed is ___. A. 1/2 km/h B. 1 km/h C. 2 km/h D. 4 km/h 2. 2

WARM UP

2. 3 Velocity In physics, Velocity: is speed in a direction. • speed: 60 km/h • velocity: 60 km/h north, or right, or down… ∆: change in… (final – initial) ∆d (df – di) m (m/s) v = t t s

2. 3 Velocity If either the speed or the direction (or both) changes, then the velocity changes. • constant speed and constant velocity are NOT the same. The car speedometer always reads 30 km/h. Is speed constant? Y Is velocity constant? N

2. 4 Acceleration We can change an object’s motion by changing its speed, its direction, or both. Acceleration is the rate at which velocity changes. ∆v (v – v ) a = t f t i acceleration can increase or decrease speed,

2. 4 Acceleration We can change an object’s motion by changing its speed, its direction, or both. Acceleration: is the rate at which velocity changes. ∆v (v – v ) a = t f t i acceleration can increase or decrease speed, deceleration is really negative acceleration (–a)

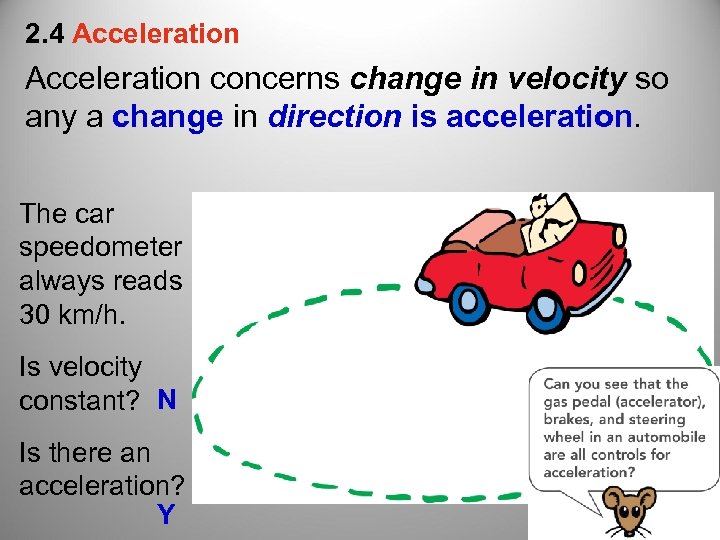2. 4 Acceleration concerns change in velocity so any a change in direction is acceleration. The car speedometer always reads 30 km/h. Is velocity constant? N Is there an acceleration? Y

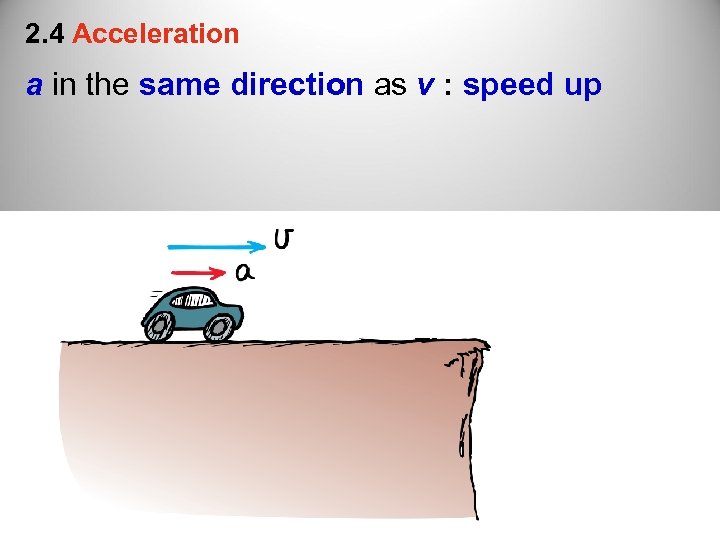2. 4 Acceleration a in the same direction as v : speed up

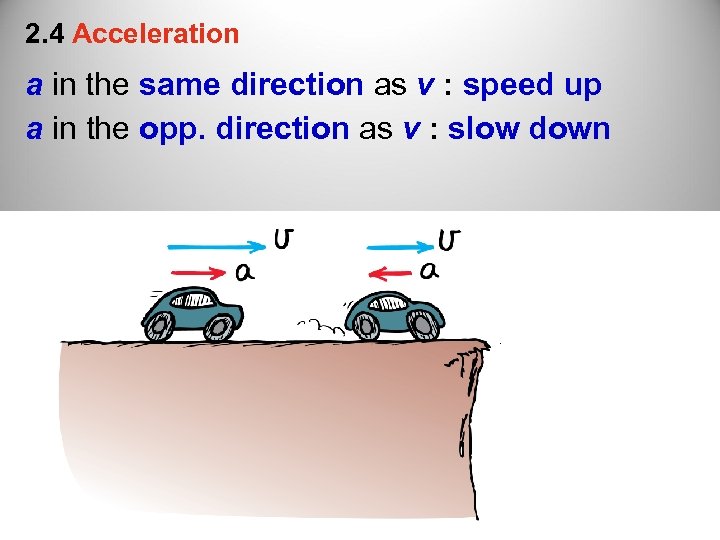2. 4 Acceleration a in the same direction as v : speed up a in the opp. direction as v : slow down

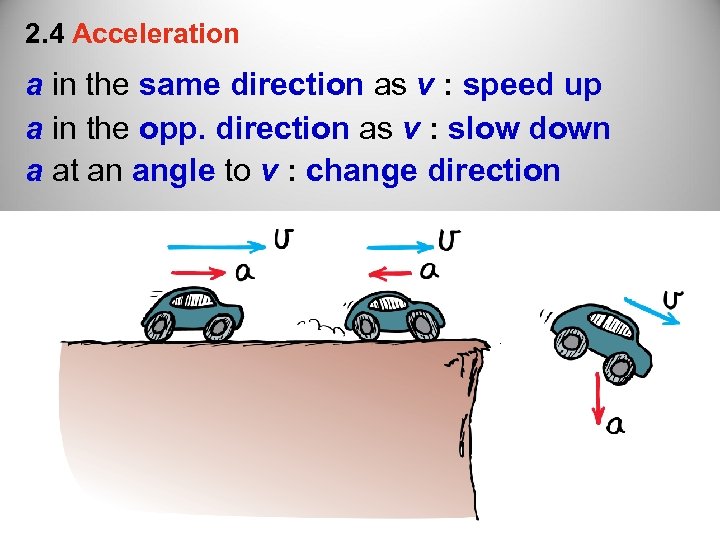2. 4 Acceleration a in the same direction as v : speed up a in the opp. direction as v : slow down a at an angle to v : change direction

2. 4 Acceleration v units are in distance per time: (m/s) • a is the change in v per change in time. ∆v a = t m/s or m s s 2 • a units are v per time: (m/s per s) or (m/s 2) • changing v from 0 m/s to 10 m/s in 1 s, a is… 10 m/s – 0 m/s 10 m/s a = = = 10 m/s 2 1 s

2. 4 Acceleration In 5 seconds a car increases its speed from 8 m/s to 18 m/s, while a truck goes from rest to 10 m/s in a straight line. Which undergoes greater acceleration? 18 m/s – 8 m/s 10 m/s acar = = = 2 m/s 2 5 s 10 m/s – 0 m/s 10 m/s atruck = = = 2 m/s 2 5 s

Quick Quiz! 1. Constant speed in a constant direction is… A. constant velocity. B. constant acceleration. C. instantaneous speed. D. average velocity. 2. 3

Quick Quiz. 2. A vehicle undergoes acceleration when it __. A. gains speed. B. decreases speed. C. changes direction. D. ALL of the above Check off the learning targets you can do after today. 2. 4

Acceleration Physics Honors

• Acceleration – The Definition The RATE of CHANGE of VELOCITY D = Change = FINAL - INITIAL Dv = Final velocity – Initial velocity

• Example: A Cessna Aircraft goes from 0 m/s to 60 m/s in 13 seconds. Calculate the aircraft’s acceleration. • 4. 62 m/s/s

• Example: The Cessna now decides to land goes from 60 m/s to 0 m/s in 11 s. Calculate the Cessna’s ? • deceleration • - 5. 45 m/s/s

• Free-Fall Acceleration If an object is in FREE FALL in the VERTICAL DIRECTION, the acceleration is due to GRAVITY. • It NEVER ceases to exist • It ALWAYS works DOWN • It is NEVER zero • This is ONLY true in a vacuum (no air)

• Acceleration due to Gravity Example: A person throws a ball straight upward into the air. Q 1: What is the Acceleration at the TOP of -9. 8 m/s/s its path? • Q 2: What is the VELOCITY at the TOP of its path? ZERO

• Acceleration due to Gravity Q 3: What is the magnitude(#value) and direction of the acceleration, HALF way up? • -9. 8 m/s/s - ALWAYS DOWNWARD • Q 4: What is the magnitude(#value) and direction of the acceleration, HALF way down? • -9. 8 m/s/s - ALWAYS DOWNWARD • THE BOTTOM LINE: EVERYTHING will accelerate at -9. 8 m/s/s in a VACUUM, • that is any situation involving NO AIR.

• Acceleration

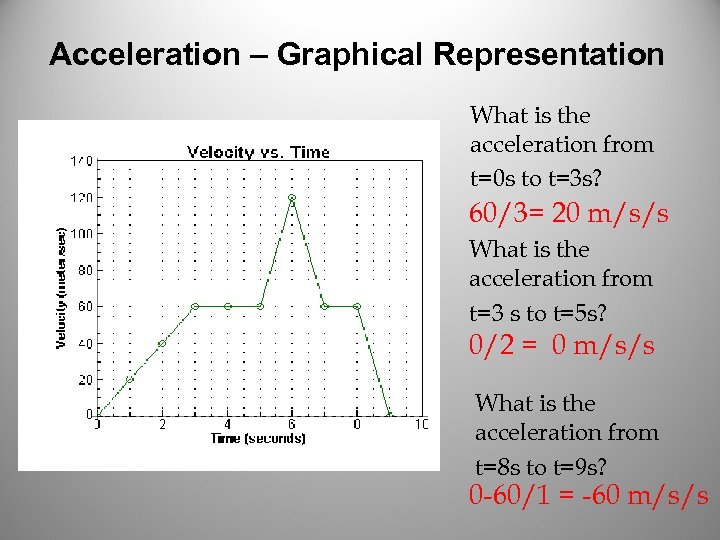Acceleration – Graphical Representation What is the acceleration from t=0 s to t=3 s? 60/3= 20 m/s/s What is the acceleration from t=3 s to t=5 s? 0/2 = 0 m/s/s What is the acceleration from t=8 s to t=9 s? 0 -60/1 = -60 m/s/s

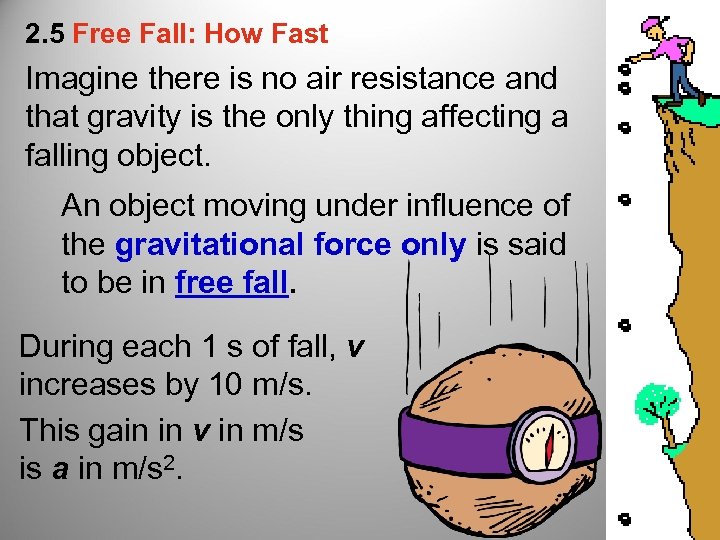2. 5 Free Fall: How Fast Imagine there is no air resistance and that gravity is the only thing affecting a falling object. An object moving under influence of the gravitational force only is said to be in free fall. During each 1 s of fall, v increases by 10 m/s. This gain in v in m/s is a in m/s 2.

2. 5 Free Fall: How Fast g is used for the acceleration due to gravity Although g varies slightly based on altitude, its average value is nearly 10 m/s 2 t = 0 s, v = 0 m/s t = 1 s, v = 10 m/s t = 2 s, v = 20 m/s t = 3 s, v = 30 m/s t = 4 s, v = 40 m/s g = – 10 m/s 2 vf = vi + at (a is g) t = 5 s, v = 50 m/s

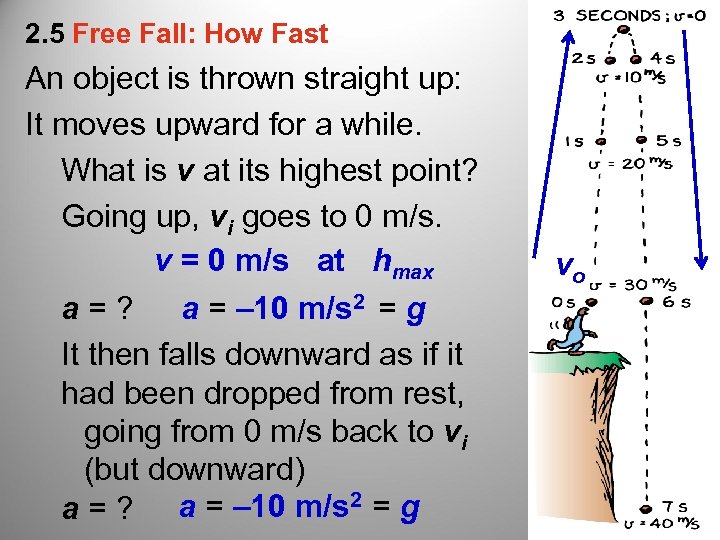2. 5 Free Fall: How Fast An object is thrown straight up: It moves upward for a while. What is v at its highest point? Going up, vi goes to 0 m/s. v = 0 m/s at hmax a = ? a = – 10 m/s 2 = g It then falls downward as if it had been dropped from rest, going from 0 m/s back to vi (but downward) a = ? a = – 10 m/s 2 = g vo

2. 5 Free Fall: How Fast What would the speedometer reading on the falling rock be 4. 5 seconds after it drops from rest? (v = ? ) v = 0 m/s + (– 10 m/s 2)(4. 5 s) v = – 45. 0 m/s How about 8 seconds after it is thrown with an initial velocity of 20 m/s downward? v = – 20 m/s + (– 10 m/s 2)(8 s) v = – 100 m/s vf = vi + at (a is g)

2. 6 Free Fall: How Far t = 0 s, v = 0 m/s, d = 0 m t = 1 s, v = 10 m/s, d = 5 m t = 2 s, v = 20 m/s, d = 20 m g = – 10 m/s 2 vf = vi + at (a is g) t = 3 s, v = 30 m/s, d = 45 m vavg = (30 + 40) d = 35 m 1 s 2 vavg = 35 m/s t = 4 s, v = 40 m/s, d = 80 m d = vit + ½at 2 1 s vavg = (40 + 50) 2 d = 45 m vavg = 45 m/s t = 5 s, v = 50 m/s, d = 125 m

2. 6 Free Fall: How Far An apple falls to the ground in 3 s. What is its speed upon striking the ground? vf = vi + at (a is g) v = 0 m/s + (10 m/s 2)(3 s) v = 30 m/s What is its vavg during the 3 s? vavg = (vf + vi) vavg = 15 m/s 2 vavg = (30 m/s + 0 m/s) 2 1 s 2 s 3 s

2. 6 Free Fall: How Far An apple falls to the ground in 3 s. How high above ground was the apple when it first dropped? vf = 30 m/s vavg = 15 m/s d = vi t + ½at 2 (a is g) 1 s d = (0 m/s)(3 s) + ½(10 m/s 2)(3 s)2 d = 45 m 2 s 3 s

2. 8 Air Resistance and Falling Objects Drop a feather and a coin and the coin reaches the floor far ahead of the feather. Why? Air resistance is responsible for these different accelerations. (not just g) In a vacuum, the feather and coin fall with exactly the same acceleration, g. With what objects might air resistance be small enough to be ignored?

Kinematics - Analyzing motion under the condition of constant acceleration Honors Physics

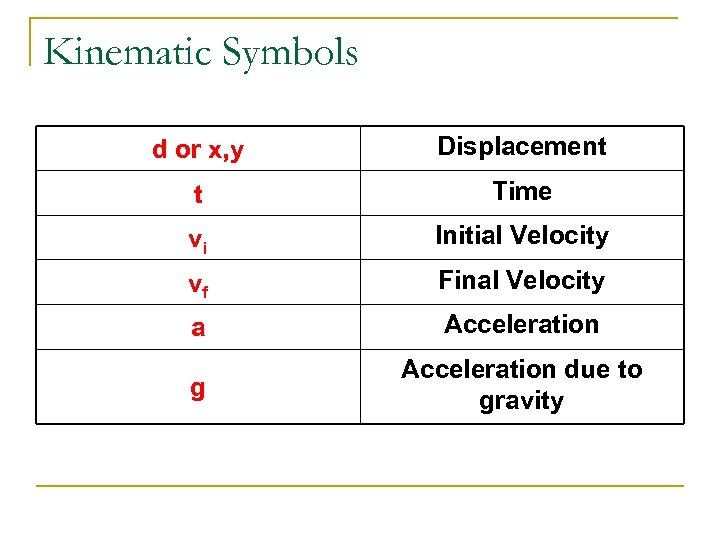Kinematic Symbols d or x, y Displacement t Time vi Initial Velocity vf Final Velocity a Acceleration g Acceleration due to gravity

Kinematic #1

Kinematic #1 Example: A boat moves slowly out of a marina (so as to not leave a wake) with a speed of 1. 50 m/s. As soon as it passes the breakwater, leaving the marina, it throttles up and accelerates at 2. 40 m/s/s. How fast is the boat moving after accelerating for 5 s? What do I know? What do I want? Vi = 1. 50 m/s vf = ? a = 2. 40 m/s/s t = 5 s 13. 5 m/s

Kinematic #2 b) How far did the boat travel during that time? 37. 5 m

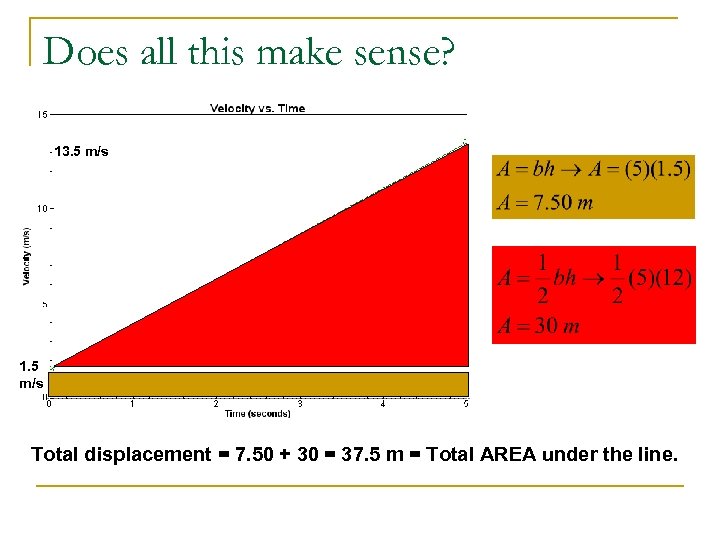Does all this make sense? 13. 5 m/s 1. 5 m/s Total displacement = 7. 50 + 30 = 37. 5 m = Total AREA under the line.

Kinematic #3 Example: You are driving through town at 12 m/s when suddenly a ball rolls out in front of your car. You apply the brakes and begin decelerating at 3. 5 m/s/s. How far do you travel before coming to a complete stop? What do I know? What do I want? Vi = 12 m/s d = ? a = -3. 5 m/s/s Vf = 0 m/s 20. 57 m

Common Problems Students Have I don’t know which equation to choose!!! Equation Missing Variable d vf t

Kinematics for the VERTICAL Direction All 3 kinematics can be used to analyze one dimensional motion in either: the X direction OR the y direction.

Examples A pitcher throws a fastball with a velocity of 43. 5 m/s. It is determined that during the windup and delivery the ball covers a displacement of 2. 5 meters. This is from the point behind the body to the point of release. Calculate the acceleration during his throwing motion. Which variable is NOT given and NOT asked for? TIME What do I know? What do I want? vi= 0 m/s a = ? d = 2. 5 m Vf = 43. 5 m/s

Examples How long does it take a car at rest to cross a 35. 0 m intersection after the light turns green, if the acceleration of the car is a constant 2. 00 m/s/s? What do I know? What do I want? Vi = 0 m/s t = ? d = 35 m a = 2. 00 m/s/s Which variable is NOT given and NOT asked for? Final Velocity

Examples A car accelerates from 12. 5 m/s to 25 m/s in 6. 0 seconds. What was the acceleration? What do I know? What do I want? vi= 12. 5 m/s a = ? vf = 25 m/s t = 6 s Which variable is NOT given and NOT asked for? DISPLACEMENT

Examples A stone is dropped from the top of a cliff. It is observed to hit the ground 5. 78 s later. How high is the cliff? What do I know? What do I want? v = 0 m/s d = ? iy g = -9. 8 m/s 2 t = 5. 78 s Which variable is NOT given and NOT asked for? Final Velocity

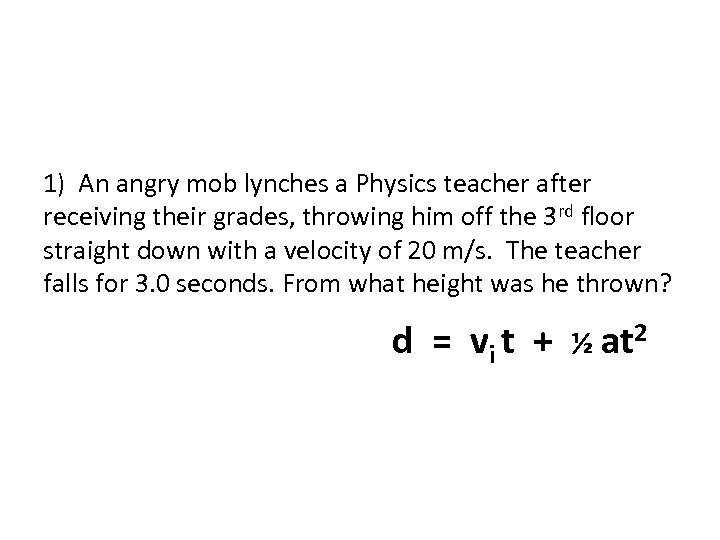1) An angry mob lynches a Physics teacher after receiving their grades, throwing him off the 3 rd floor straight down with a velocity of 20 m/s. The teacher falls for 3. 0 seconds. From what height was he thrown? d = vi t + ½ at 2

2) Find the uniform acceleration that causes a car’s velocity to change from 32 m/s to 96 m/s in an 8. 0 s period. vf = vi + at

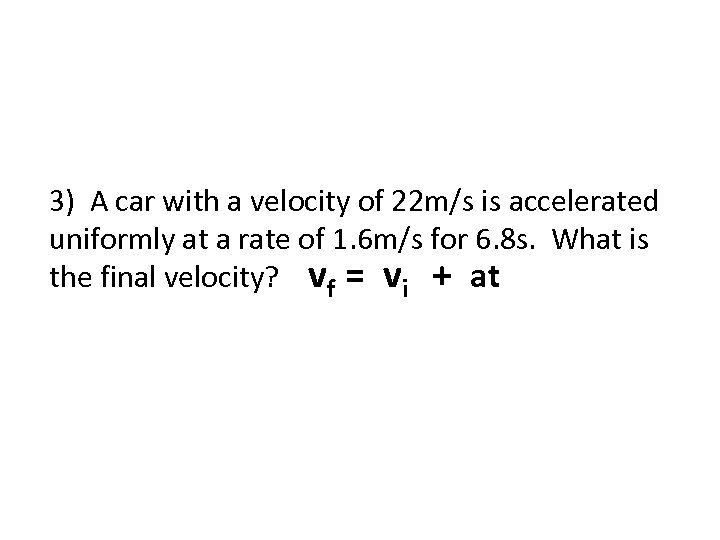3) A car with a velocity of 22 m/s is accelerated uniformly at a rate of 1. 6 m/s for 6. 8 s. What is the final velocity? vf = vi + at

4) An airplane starts from rest and accelerates at a constant 3. 0 m/s 2 for 30 s before leaving ground. a) How far did it move? d = vi t + ½ at 2 b) How fast was it going at liftoff? vf = vi + at

5) Your sister drops your house keys down to you from the second floor window. If you catch them 4. 3 m from where dropped them… what is the velocity of the keys when you catch them? vf 2 = vi 2 + 2 ad

6) A train is traveling at 6. 4 m/s and accelerates d = vi t + 2 over a distance of 100 m. What is its’ ½ at 2 at 0. 10 m/s vf 2 = vi 2 + 2 ad final velocity? v 2 = v 2 + 2 ad vf = vi + at f i

d = vi t + ½ at 2 vf 2 = vi 2 + 2 ad vf = vi + at

Quick Quiz! 1. In a vacuum tube, a feather is seen to fall as fast as a coin. This is because … A. gravity doesn’t act in a vacuum. B. air resistance doesn’t act in a vacuum. C. greater air resistance acts on the coin. D. gravity is greater in a vacuum. 2. 8

Quick Quiz. 2. If a falling object gains 10 m/s each second it falls, its acceleration can be expressed as _____. A. 10 m/s/s B. 10 m/s 2 C. v = gt D. both A and B 2. 5

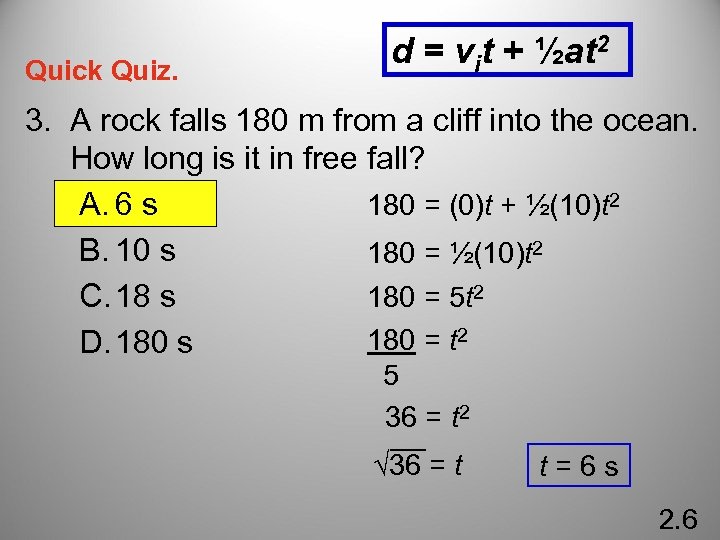Quick Quiz. d = vit + ½at 2 3. A rock falls 180 m from a cliff into the ocean. How long is it in free fall? A. 6 s 180 = (0)t + ½(10)t 2 B. 10 s 180 = ½(10)t 2 C. 18 s 180 = 5 t 2 180 = t 2 D. 180 s 5 36 = t 2 √ 36 = t t = 6 s 2. 6

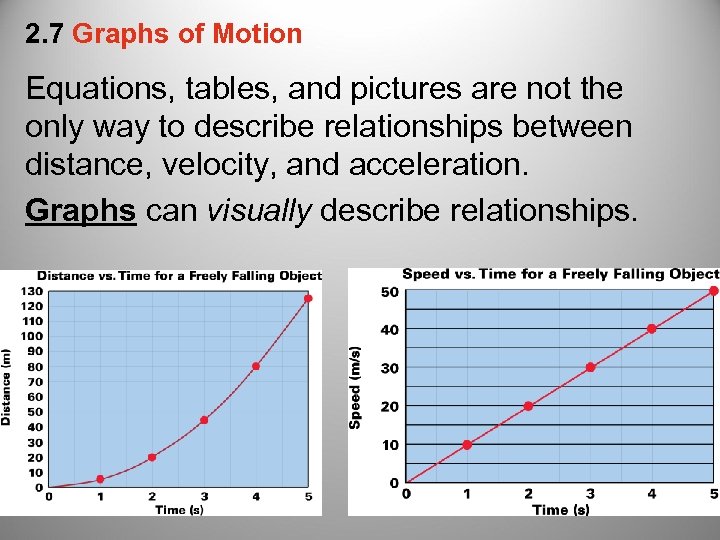2. 7 Graphs of Motion Equations, tables, and pictures are not the only way to describe relationships between distance, velocity, and acceleration. Graphs can visually describe relationships.

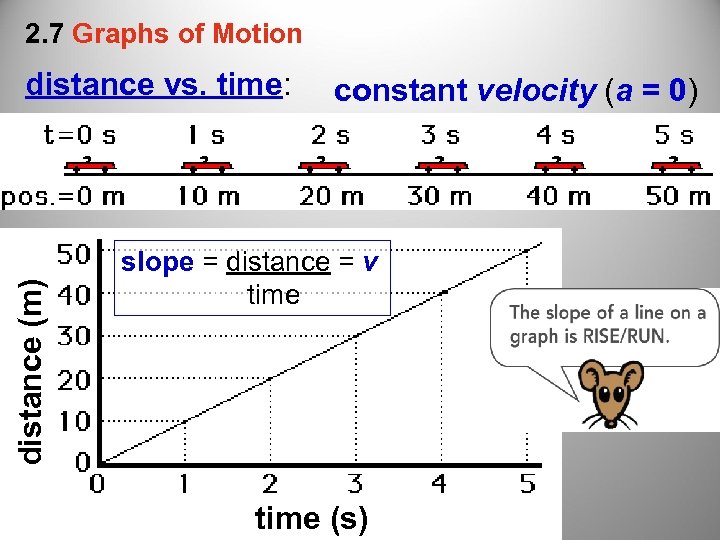2. 7 Graphs of Motion distance (m) distance vs. time: constant velocity (a = 0) slope = distance = v time (s)

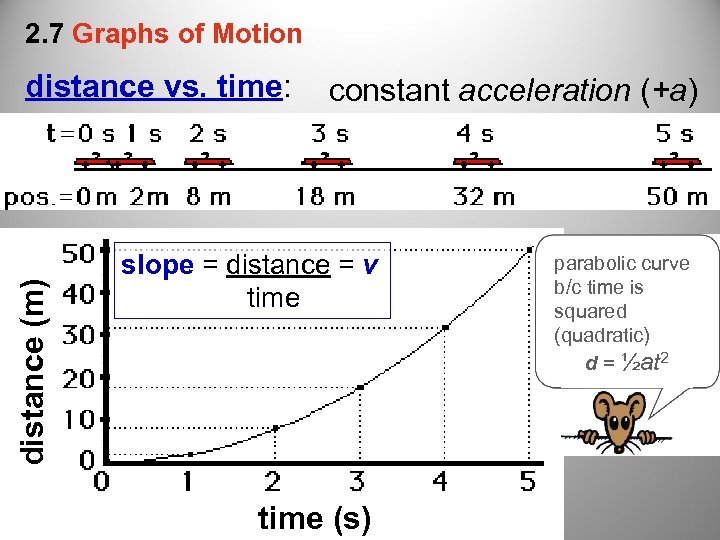2. 7 Graphs of Motion distance (m) distance vs. time: constant acceleration (+a) slope = distance = v time (s) parabolic curve b/c time is squared (quadratic) d = ½at 2

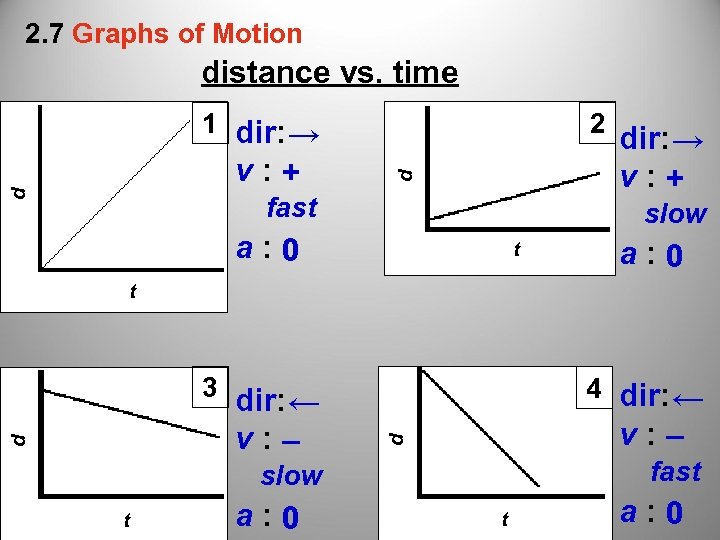2. 7 Graphs of Motion distance vs. time d v : + 2 d 1 dir: → fast dir: → v : + slow a : 0 t dir: ← v : – 4 dir: ← v : – d d 3 fast slow t a : 0

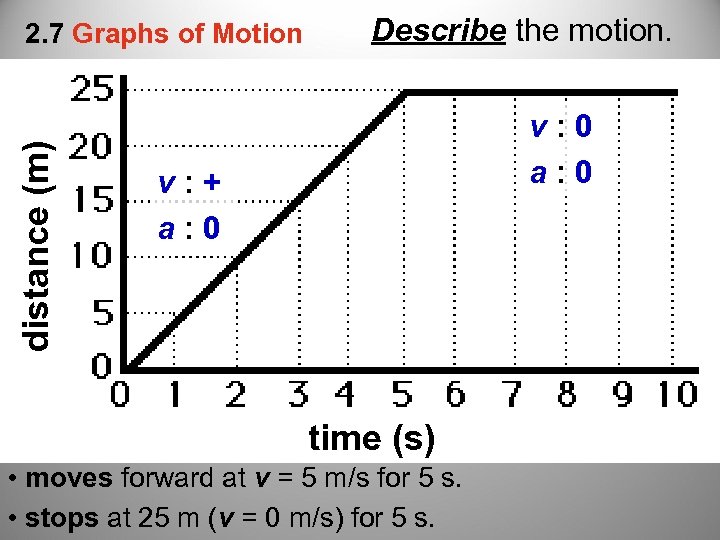distance (m) 2. 7 Graphs of Motion Describe the motion. v : 0 a : 0 v : + a : 0 time (s) • moves forward at v = 5 m/s for 5 s. • stops at 25 m (v = 0 m/s) for 5 s.

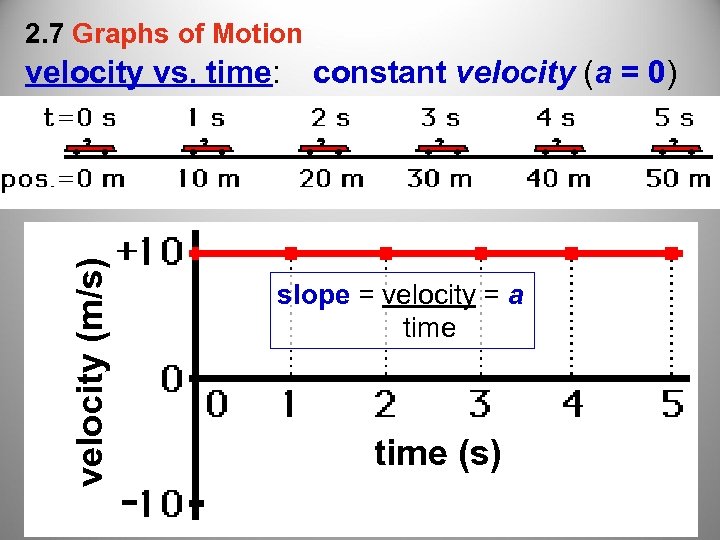2. 7 Graphs of Motion velocity (m/s) velocity vs. time: constant velocity (a = 0) slope = velocity = a time (s)

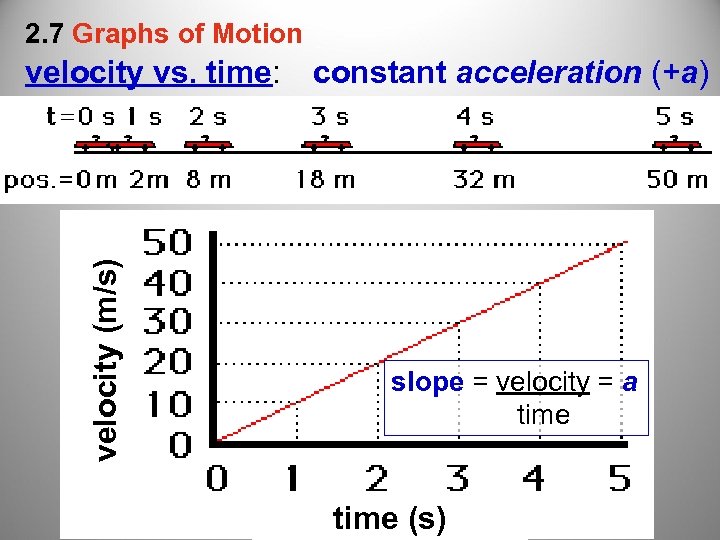2. 7 Graphs of Motion velocity (m/s) velocity vs. time: constant acceleration (+a) slope = velocity = a time (s)

2. 7 Graphs of Motion dir: right v : + (constant) a : 0 dir: right v : + (faster) a : + dir: left v : – (slower) a : + dir: left v : – (constant) a : 0 dir: right v : + (slower) a : – dir: left v : – (faster) a : –

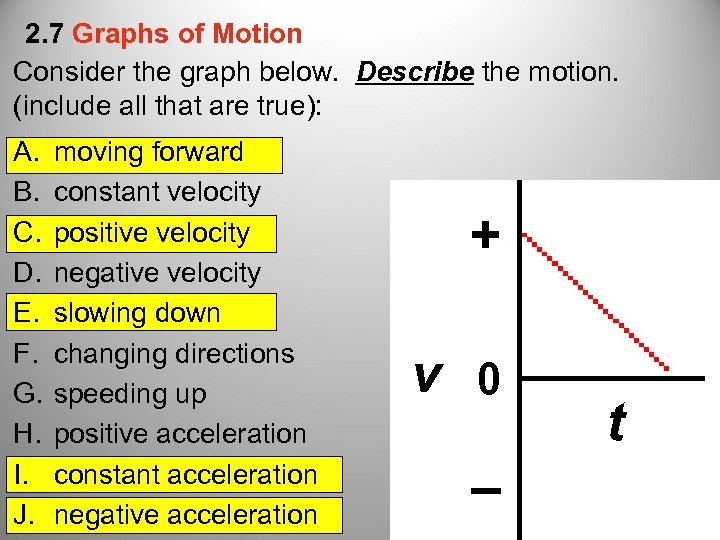2. 7 Graphs of Motion Consider the graph below. Describe the motion. (include all that are true): A. B. C. D. E. F. G. H. I. J. moving forward constant velocity positive velocity negative velocity slowing down changing directions speeding up positive acceleration constant acceleration negative acceleration + v 0 – t

Quick Quiz! The slope of a velocity-versus-time graph represents ____. A. distance B. velocity C. acceleration D. time Check off the learning targets you can do after today.

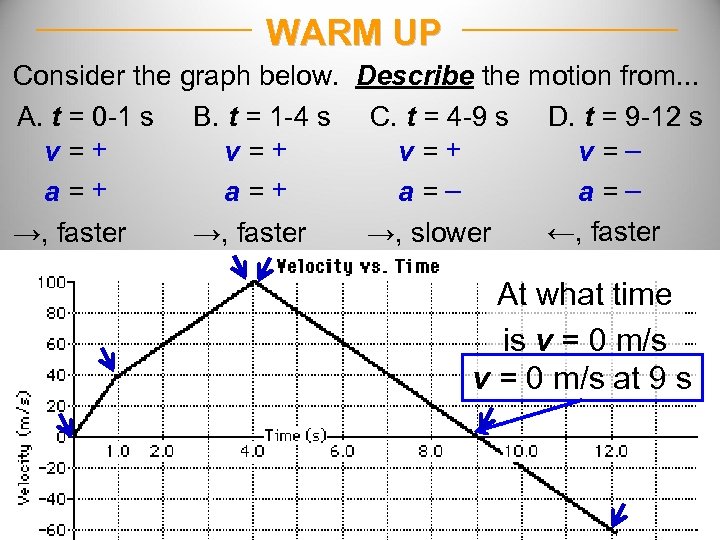WARM UP Consider the graph below. Describe the motion from. . . A. t = 0 -1 s B. t = 1 -4 s C. t = 4 -9 s D. t = 9 -12 s v = – v = + a = – a = + a = – ←, faster →, slower At what time is v = 0 m/s at 9 s

Equations Summary N NOT given on test distance speed = time N ∆d v = t vavg = (vf + vi) 2 ∆v a = t vf = vi + at vf 2 = vi 2 + 2 ad d = vit + ½at 2 given on test g = – 10 m/s 2

WS Motion Graphs Begin your worksheet now. We will take all of class tomorrow to finish it and the rest of your Text Questions.

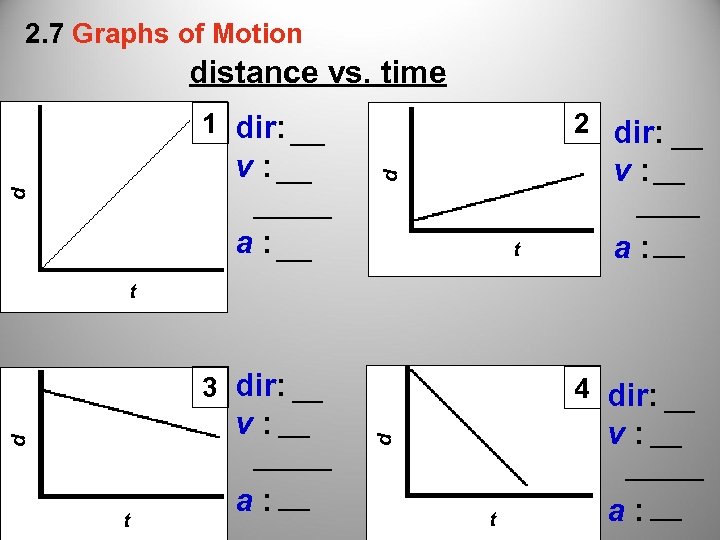2. 7 Graphs of Motion distance vs. time v : __ d 1 dir: __ d _____ a : __ t 2 dir: __ v : __ ____ a : __ t 3 dir: __ v : __ _____ a : __ d d t t 4 dir: __ v : __ _____ a : __

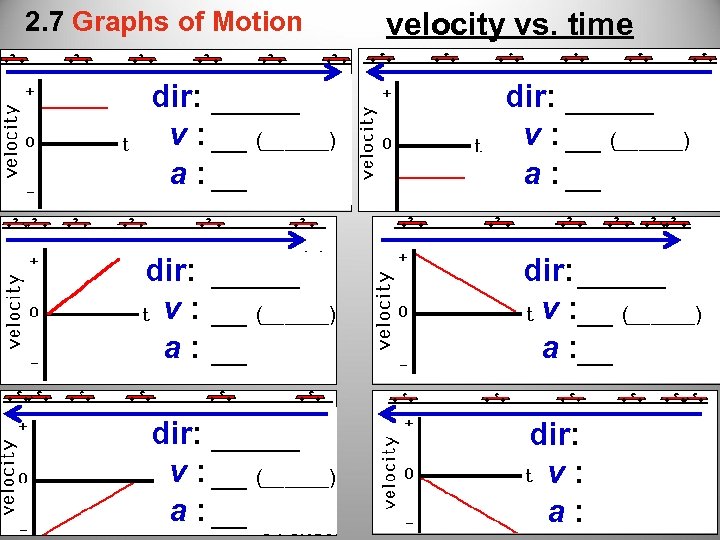2. 7 Graphs of Motion dir: _____ v : __ (______) a : __ velocity vs. time dir: _____ v : __ (______) a : __ dir: _____ v : __ (______) a : __ dir: _____ v : __ (______) __ a :

https: //www. youtube. com/watch? v=r. D 0 tmg. Mdb. Qg VIDEO – Part 1 (7: 19) Acceleration & Velocity Graphs

https: //www. youtube. com/watch? v=JFZ 2 W 5 Pwlr. Y VIDEO – Part 2 (9: 53) Acceleration & Velocity Graphs

https: //www. youtube. com/watch? v=n. Ph. Rrhb 99 r. Y VIDEO – Part 3 (7: 45) Acceleration & Velocity Graphs

QUIZ 2 A NAME 1) 2) 3) 4) 5) Date Quiz 2 A Pd __ 6) 7) 8) 9) 10)

HEY… guess what day it is?

1. The difference between speed and velocity is that velocity indicates _____ and direction. A) Distance B) speed C) time D) Acceleration 2. The change in velocity over time is defined as: A) Distance B) Speed C) Acceleration D) motion E) frame of reference 3. An object that is accelerating may be doing which of the following? I. changing direction II. gaining speed III. at rest IV. slowing down A) II only B) II and IV only C) I, II, and IV only D) I, III, and IV

4. Suppose you are in a car that is going around a curve. The speedometer reads a constant 30 miles per hour. Which is TRUE? I. The car’s direction is changing. II. The car is accelerating III. The car’s velocity is zero. A) I only B) II only C) I and II only D) II and III only E) I, II, and III

5. As an object falls freely in a tube filled with air, which of the following is TRUE? I. velocity decreases II. velocity is constant III. acceleration is zero IV. acceleration is constant A) II only B) III only C) IV only Measure # Mass (g) D) I, IV only E) II, III only 1 2. 02 g ? 2 6. If you drop a feather and a coin at the 1. 98 g ? ? 3 same time in a vacuum, which will 2. 03 g ? reach the bottom of the tube first? A) coin B) feather C) both at the same time

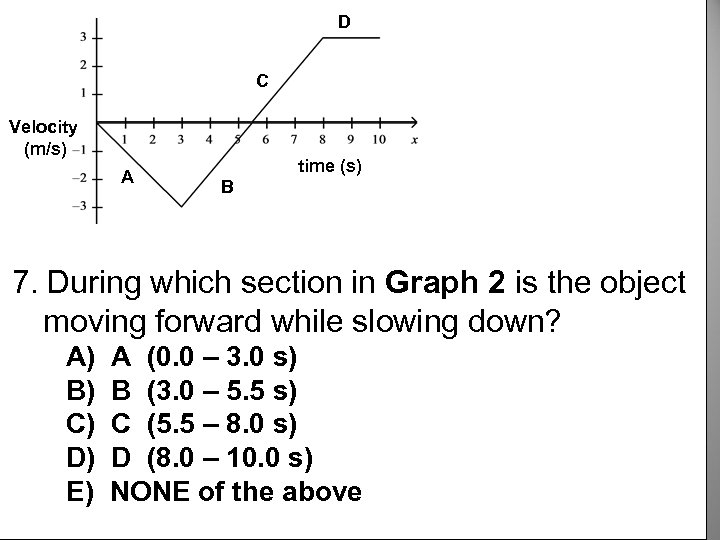D C Velocity (m/s) A time (s) B 7. During which section in Graph 2 is the object moving forward while slowing down? A) A (0. 0 – 3. 0 s) B) B (3. 0 – 5. 5 s) C) C (5. 5 – 8. 0 s) D) D (8. 0 – 10. 0 s) E) NONE of the above

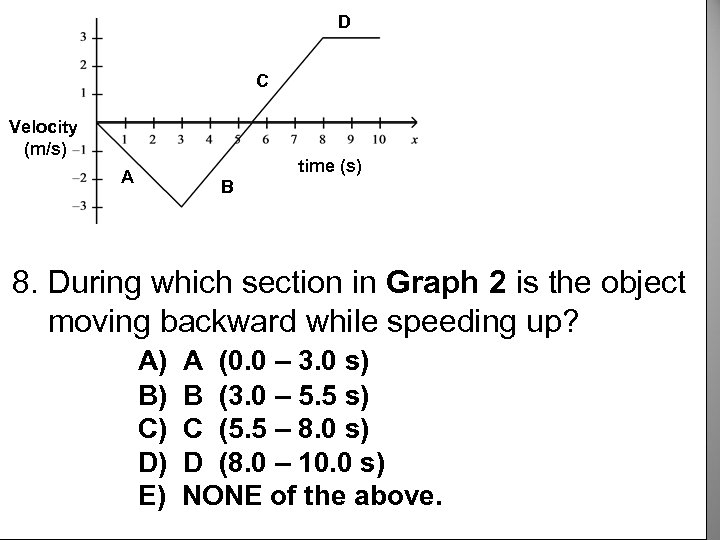D C Velocity (m/s) A time (s) B 8. During which section in Graph 2 is the object moving backward while speeding up? A) A (0. 0 – 3. 0 s) B) B (3. 0 – 5. 5 s) C) C (5. 5 – 8. 0 s) D) D (8. 0 – 10. 0 s) E) NONE of the above.

9. A hiker covered 3 km in 2 hour on a hiking trail, and then 5 km in 2 hours on the trail before reaching her destination. What was the hiker’s average speed? A) 2 km/h B) 4 km/h C) 8 km/h D) 15 km/h 10. A car moving at 22 m/s comes to a complete stop in 5 seconds. What is the car’s acceleration? A) 0. 23 m/s 2 B) 4. 4 m/s 2 C) – 0. 23 m/s 2 D) – 4. 4 m/s 2

QUIZ 2 A NAME 1) 2) 3) 4) 5) Date Quiz 2 A Pd __ 6) #correct 7) 10 8) 9) 10)