Warm Up Convert each measurement 1 6 ft

Warm Up Convert each measurement. 1. 6 ft 3 in. to inches 75 in. 2. 5 m 38 cm to centimeters 538 cm Find the perimeter and area of each polygon. 3. square with side length 13 cm P = 52 cm, A =169 cm 2 4. rectangle with length 5. 8 m and width 2. 5 m P =16. 6 m, A = 14. 5 m 2

A scale drawing represents an object as smaller than or larger than its actual size. The drawing’s scale is the ratio of any length in the drawing to the corresponding actual length. For example, on a map with a scale of 1 cm : 1500 m, one centimeter on the map represents 1500 m in actual distance. Remember! A proportion may compare measurements that have different units.

CHAPTER 6. 3 The scale on the map of a city is 1/4 inch equals 2 miles. On the map, the width of the city at its widest point is 3 3/4 inches. The city hosts a bicycle race across town at its widest point. Tashawna bikes at 10 miles per hour. How long will it take her to complete the race?

The scale on the map of a city is 1/4 inch equals 2 miles. On the map, the width of the city at its widest point is 3 3/4 inches. The city hosts a bicycle race across town at its widest point. Tashawna bikes at 10 miles per hour. How long will it take her to complete the race? ¼ inches = 2 miles x = 30 miles, town at widest pt. 3 ¾ inches x miles ? Time to complete race = 30 miles * 1 hour = 3 hours 10 miles ANSWER: 3 hours

A historic train ride is planned between two landmarks on the Lewis and Clark Trail. The scale on a map that includes the two landmarks is 3 centimeters = 125 miles. The distance between the two landmarks on the map is 1. 5 centimeters. If the train travels at an average rate of 50 miles per hour, how long will the trip between the landmarks take?

A historic train ride is planned between two landmarks on the Lewis and Clark Trail. The scale on a map that includes the two landmarks is 3 centimeters = 125 miles. The distance between the two landmarks on the map is 1. 5 centimeters. If the train travels at an average rate of 50 miles per hour, how long will the trip between the landmarks take? 3 cm = 125 mi = 62. 5 mi, distance bewt landmarks 1. 5 cm x 62. 5 mi x 1 hr = 1. 25 hours or 1 hour 15 minutes 50 mi

Scale Problems On a Wisconsin road map, Kristin measured a distance of 11 in. from Madison to Wausau. The scale of this map is 1 inch: 13 miles. What is the actual distance between Madison and Wausau to the nearest mile?

Example 2 Continued To find the actual distance x write a proportion comparing the map distance to the actual distance. Cross Products Prop. x 145 Simplify. The actual distance is 145 miles, to the nearest mile.

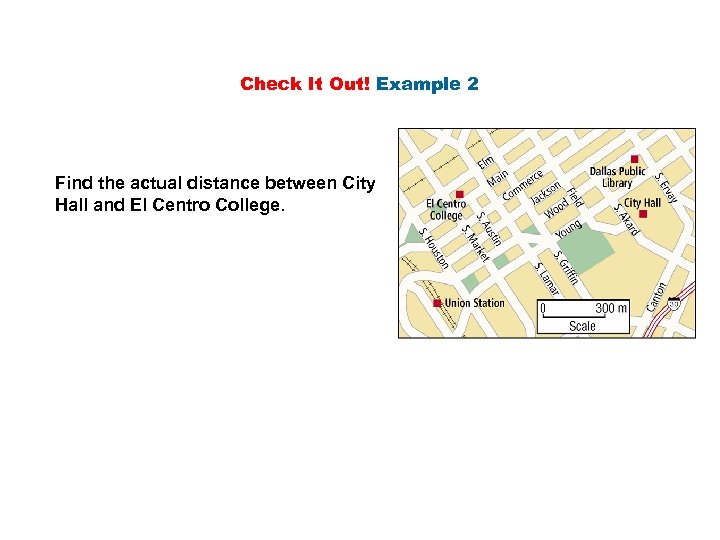Check It Out! Example 2 Find the actual distance between City Hall and El Centro College.

Check It Out! Example 2 Continued To find the actual distance x write a proportion comparing the map distance to the actual distance. 1 x = 3(300) x 900 Cross Products Prop. Simplify. The actual distance is 900 meters, or 0. 9 km.

INDIRECT MEASUREMENT Josh wanted to measure the height of the Sears Tower in Chicago. He used a 12 -foot light pole and measured its shadow at 1 P. M. The length of the shadow was 2 feet. Then he measured the length of the Sears Tower’s shadow and it was 242 feet at that time. What is the height of the Sears Tower? **In a shadow problem, we assume that a right triangle is formed by the sun’s ray from the top of the object to the end of the shadow.

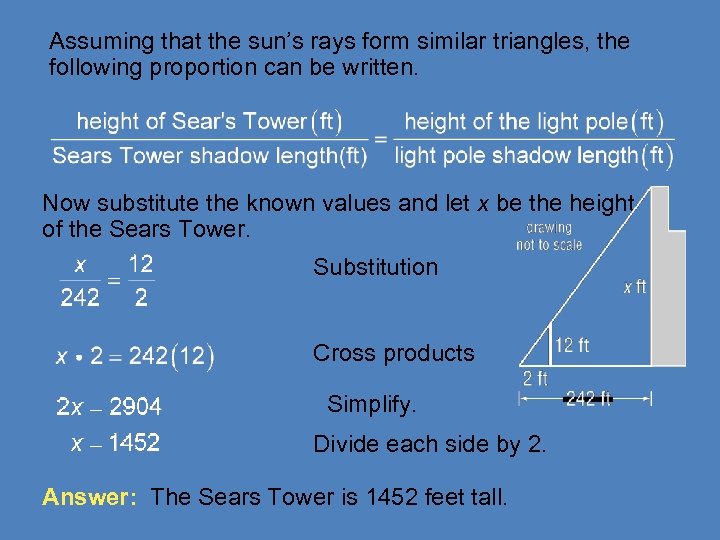Assuming that the sun’s rays form similar triangles, the following proportion can be written. Now substitute the known values and let x be the height of the Sears Tower. Substitution Cross products Simplify. Divide each side by 2. Answer: The Sears Tower is 1452 feet tall.

Nina was curious about the height of the Eiffel Tower. She used a 1. 2 meter model of the tower and measured its shadow at 2 p. m. The length of the shadow was 0. 9 m. Then, she measured the Eiffel Tower’s shadow, and it was 240 meters. What is the height of the Eiffel Tower? Model height = tower height Model shadow tower shadow 1. 2 m = tower height 0. 9 m 240 m (1. 2 m)(240 m) = tower height 0. 9 m 333. 3 m = tower height

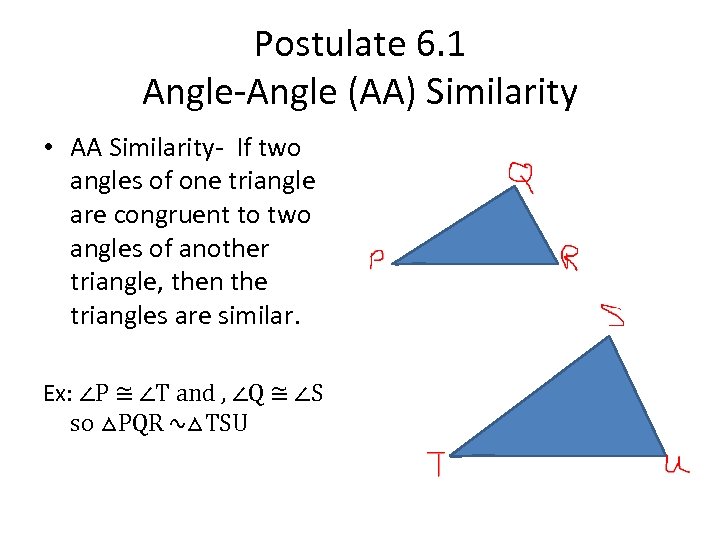Postulate 6. 1 Angle-Angle (AA) Similarity • AA Similarity- If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. Ex: ∠P ≅ ∠T and , ∠Q ≅ ∠S so △PQR ∿△TSU

There are several ways to prove certain triangles are similar. The following postulate, as well as the SSS and SAS Similarity Theorems, will be used in proofs just as SSS, SAS, ASA, HL, and AAS were used to prove triangles congruent.

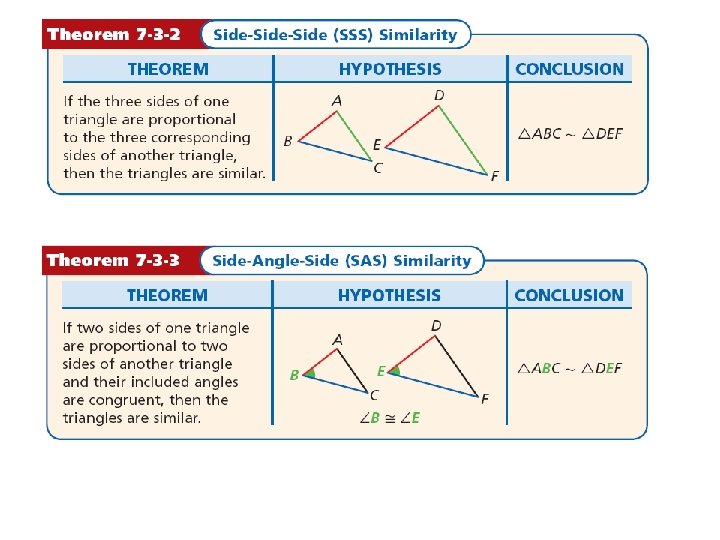
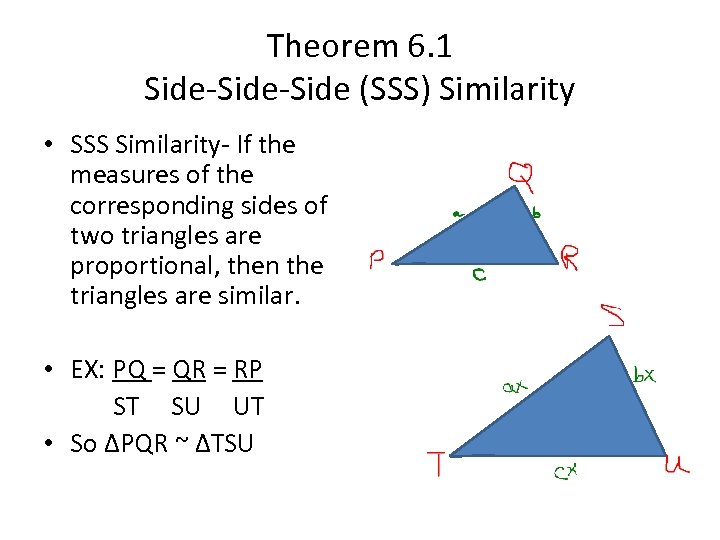Theorem 6. 1 Side-Side (SSS) Similarity • SSS Similarity- If the measures of the corresponding sides of two triangles are proportional, then the triangles are similar. • EX: PQ = QR = RP ST SU UT • So ∆PQR ~ ∆TSU

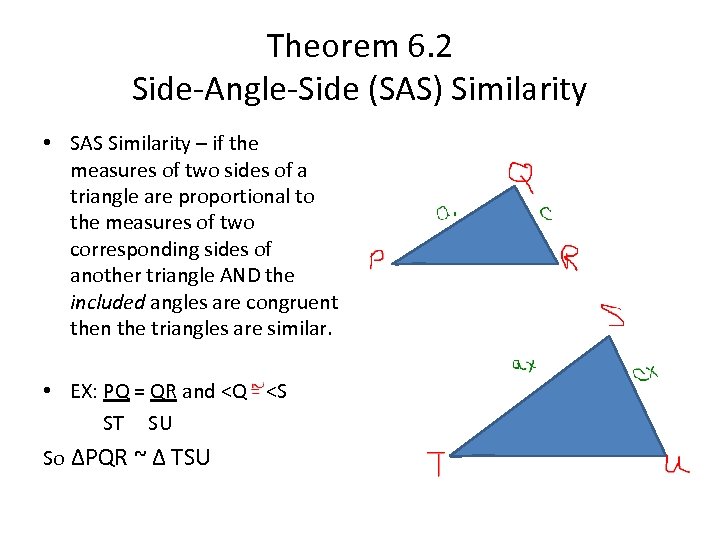Theorem 6. 2 Side-Angle-Side (SAS) Similarity • SAS Similarity – if the measures of two sides of a triangle are proportional to the measures of two corresponding sides of another triangle AND the included angles are congruent then the triangles are similar. • EX: PQ = QR and

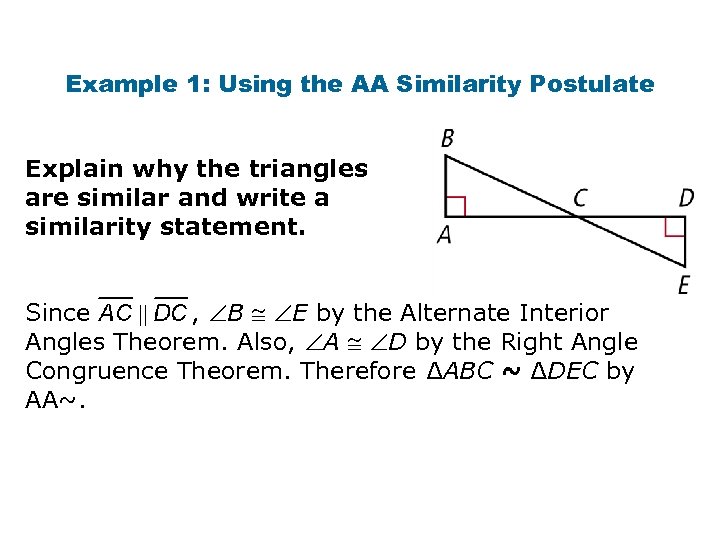Example 1: Using the AA Similarity Postulate Explain why the triangles are similar and write a similarity statement. Since , B E by the Alternate Interior Angles Theorem. Also, A D by the Right Angle Congruence Theorem. Therefore ∆ABC ~ ∆DEC by AA~.

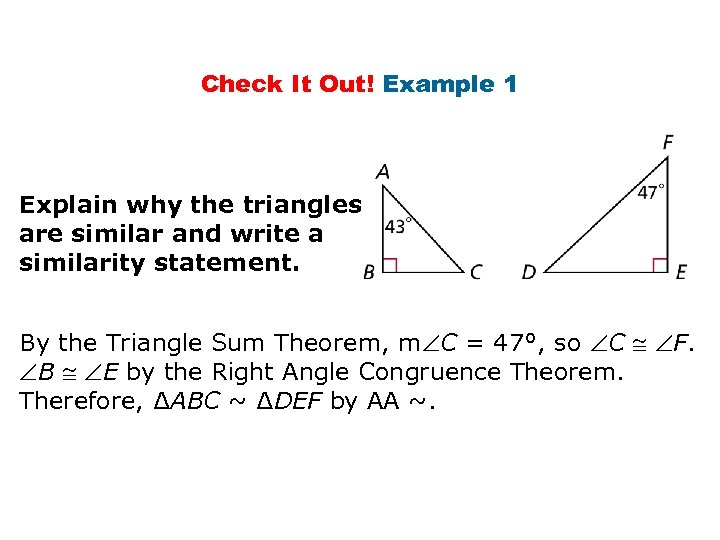Check It Out! Example 1 Explain why the triangles are similar and write a similarity statement. By the Triangle Sum Theorem, m C = 47°, so C F. B E by the Right Angle Congruence Theorem. Therefore, ∆ABC ~ ∆DEF by AA ~.

Example 2 A: Verifying Triangle Similarity Verify that the triangles are similar. ∆PQR and ∆STU Therefore ∆PQR ~ ∆STU by SSS ~.

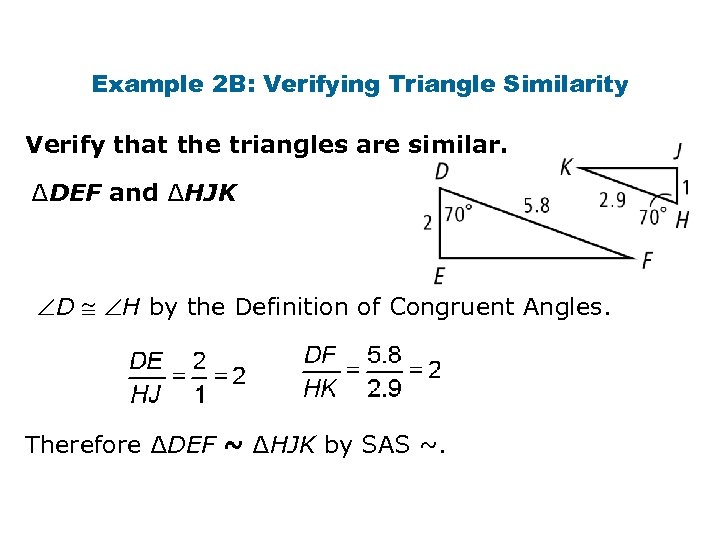Example 2 B: Verifying Triangle Similarity Verify that the triangles are similar. ∆DEF and ∆HJK D H by the Definition of Congruent Angles. Therefore ∆DEF ~ ∆HJK by SAS ~.

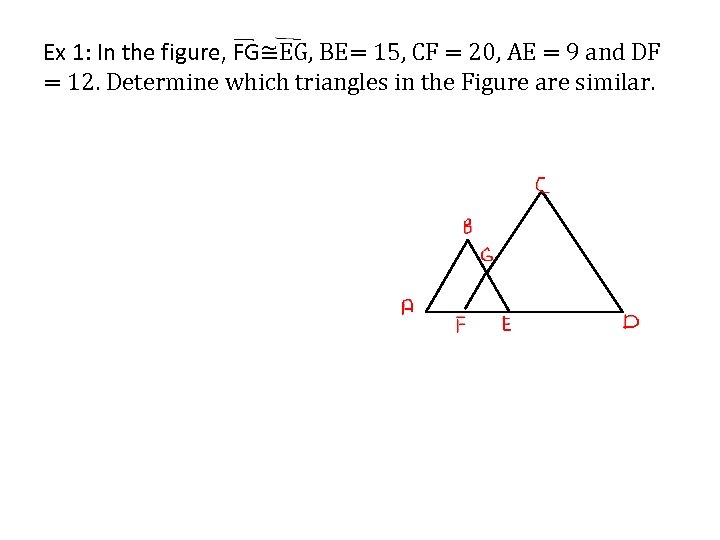Ex 1: In the figure, FG≅EG, BE= 15, CF = 20, AE = 9 and DF = 12. Determine which triangles in the Figure are similar.

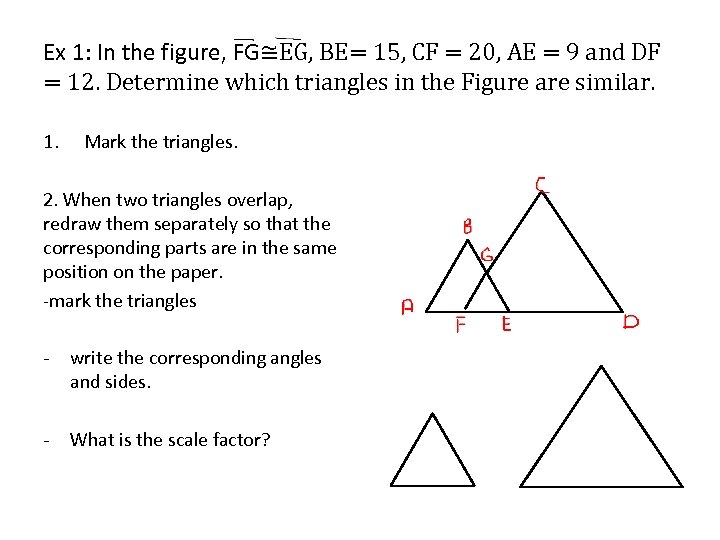Ex 1: In the figure, FG≅EG, BE= 15, CF = 20, AE = 9 and DF = 12. Determine which triangles in the Figure are similar. 1. Mark the triangles. 2. When two triangles overlap, redraw them separately so that the corresponding parts are in the same position on the paper. -mark the triangles - write the corresponding angles and sides. - What is the scale factor?

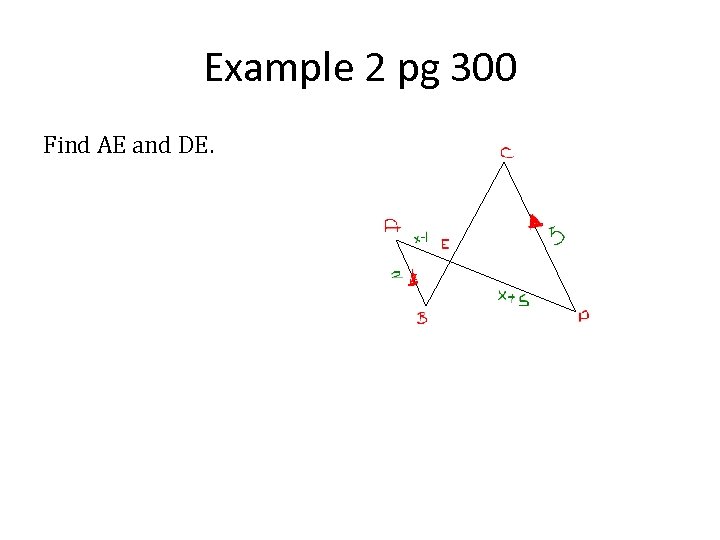Example 2 pg 300 Find AE and DE.

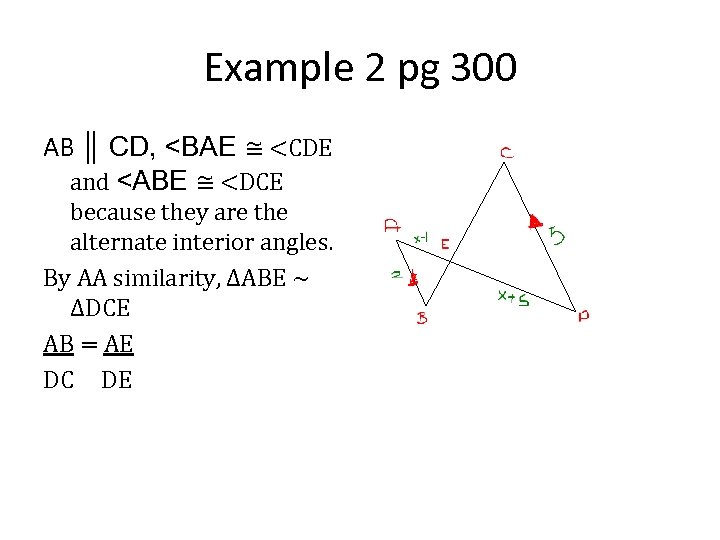Example 2 pg 300 AB ║ CD,

Warm Up Solve each proportion. 1. 2. 3. z = ± 10 x=8 4. If ∆QRS ~ ∆XYZ, identify the pairs of congruent angles and write 3 proportions using pairs of corresponding sides. Q X; R Y; S Z; QR = RS = QS XY YZ XZ

INDIRECT MEASUREMENT On her trip along the East coast, Jennie stops to look at the tallest lighthouse in the U. S. located at Cape Hatteras, North Carolina. At that particular time of day, Jennie measures her shadow to be 1 feet 6 inches in length and the length of the shadow of the lighthouse to be 53 feet 6 inches. Jennie knows that her height is 5 feet 6 inches. What is the height of the Cape Hatteras lighthouse to the nearest foot?

INDIRECT MEASUREMENT On her trip along the East coast, Jennie stops to look at the tallest lighthouse in the U. S. located at Cape Hatteras, North Carolina. At that particular time of day, Jennie measures her shadow to be 1 feet 6 inches in length and the length of the shadow of the lighthouse to be 53 feet 6 inches. Jennie knows that her height is 5 feet 6 inches. What is the height of the Cape Hatteras lighthouse to the nearest foot? Jennie shadow 1 ft 6 in = 1. 5 ft Jennie’s height 5 ft 6 in = 5. 5 ft Light house shadow 53 ft 6 in = 53. 5 ft Jennie shadow = light house shadow 1. 5 ft = 53. 5 ft 1. 5 X = (53. 5)(5. 5) Jennie height light house height X = 196 ft Answer: 196 ft 5. 5 ft X

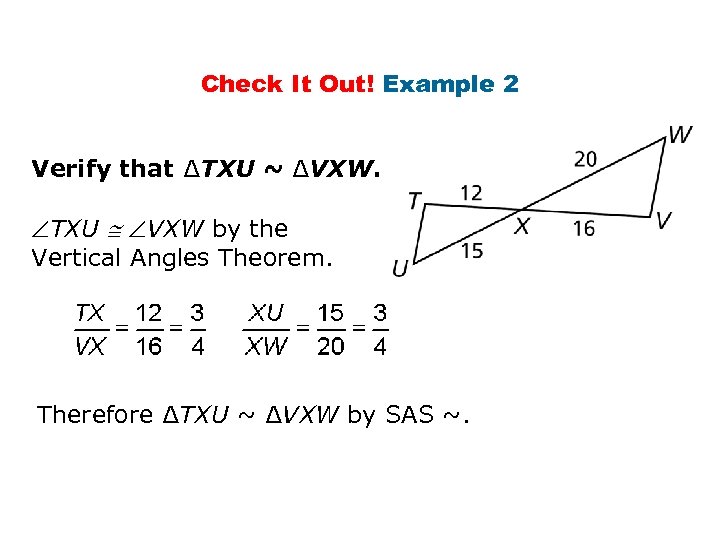Check It Out! Example 2 Verify that ∆TXU ~ ∆VXW. TXU VXW by the Vertical Angles Theorem. Therefore ∆TXU ~ ∆VXW by SAS ~.

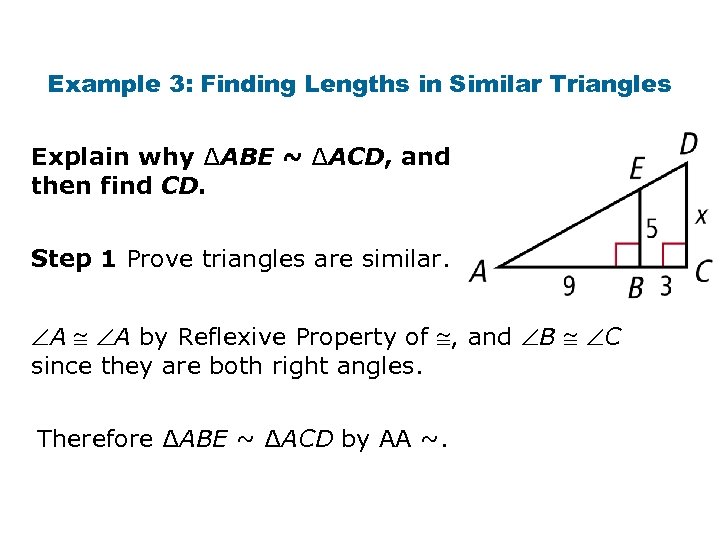Example 3: Finding Lengths in Similar Triangles Explain why ∆ABE ~ ∆ACD, and then find CD. Step 1 Prove triangles are similar. A A by Reflexive Property of , and B C since they are both right angles. Therefore ∆ABE ~ ∆ACD by AA ~.

Example 3 Continued Step 2 Find CD. Corr. sides are proportional. Seg. Add. Postulate. x(9) = 5(3 + 9) 9 x = 60 Substitute x for CD, 5 for BE, 3 for CB, and 9 for BA. Cross Products Prop. Simplify. Divide both sides by 9.

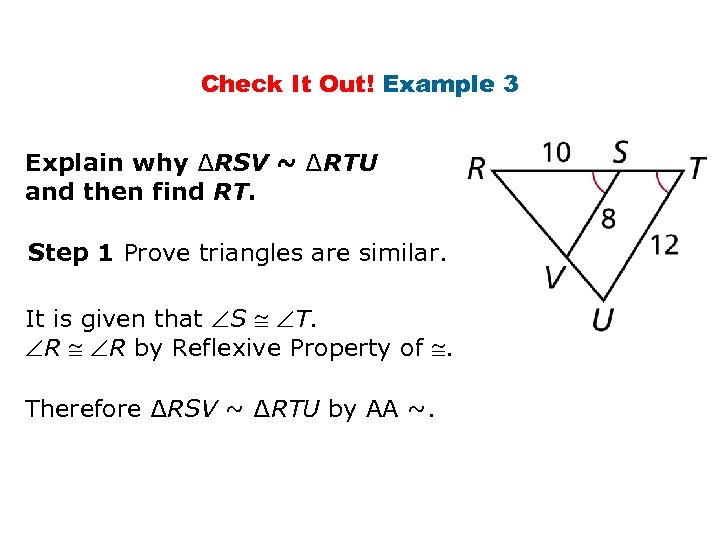Check It Out! Example 3 Explain why ∆RSV ~ ∆RTU and then find RT. Step 1 Prove triangles are similar. It is given that S T. R R by Reflexive Property of . Therefore ∆RSV ~ ∆RTU by AA ~.

Check It Out! Example 3 Continued Step 2 Find RT. Corr. sides are proportional. Substitute RS for 10, 12 for TU, 8 for SV. RT(8) = 10(12) Cross Products Prop. 8 RT = 120 RT = 15 Simplify. Divide both sides by 8.

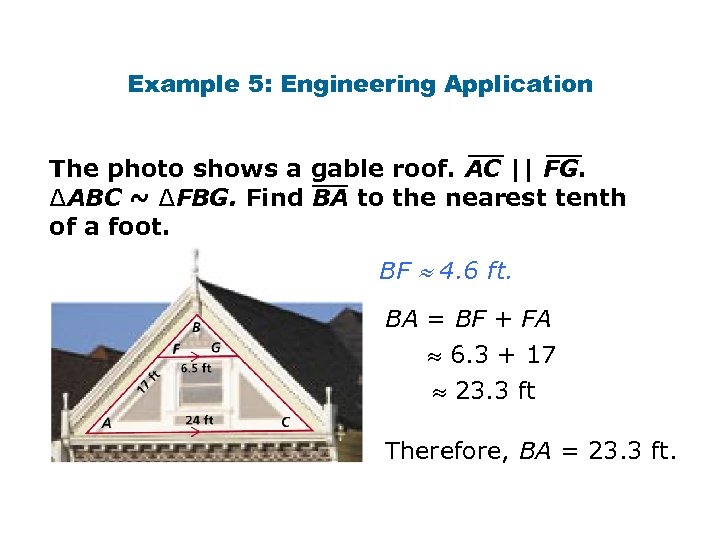Example 5: Engineering Application The photo shows a gable roof. AC || FG. ∆ABC ~ ∆FBG. Find BA to the nearest tenth of a foot. BF 4. 6 ft. BA = BF + FA 6. 3 + 17 23. 3 ft Therefore, BA = 23. 3 ft.

Check It Out! Example 5 What if…? If AB = 4 x, AC = 5 x, and BF = 4, find FG. Corr. sides are proportional. Substitute given quantities. 4 x(FG) = 4(5 x) Cross Prod. Prop. FG = 5 Simplify.

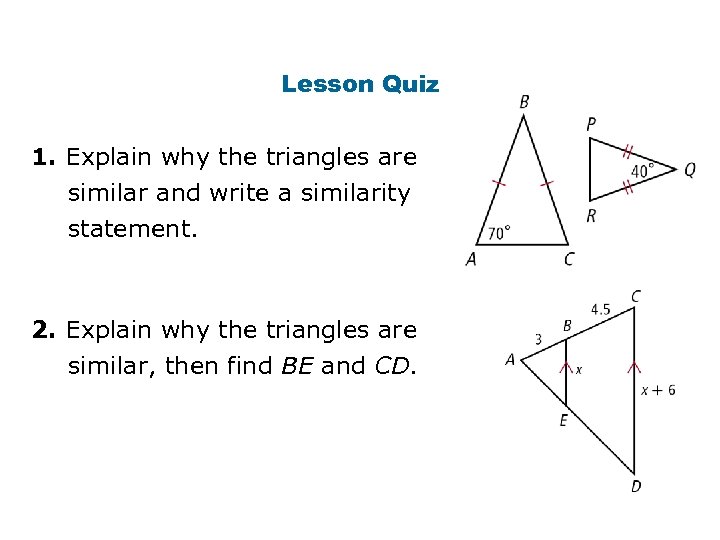Lesson Quiz 1. Explain why the triangles are similar and write a similarity statement. 2. Explain why the triangles are similar, then find BE and CD.

Lesson Quiz 1. By the Isosc. ∆ Thm. , A C, so by the def. of , m C = m A. Thus m C = 70° by subst. By the ∆ Sum Thm. , m B = 40°. Apply the Isosc. ∆ Thm. and the ∆ Sum Thm. to ∆PQR. m R = m P = 70°. So by the def. of , A P, and C R. Therefore ∆ABC ~ ∆PQR by AA ~. 2. A A by the Reflex. Prop. of . Since BE || CD, ABE ACD by the Corr. s Post. Therefore ∆ABE ~ ∆ACD by AA ~. BE = 4 and CD = 10.

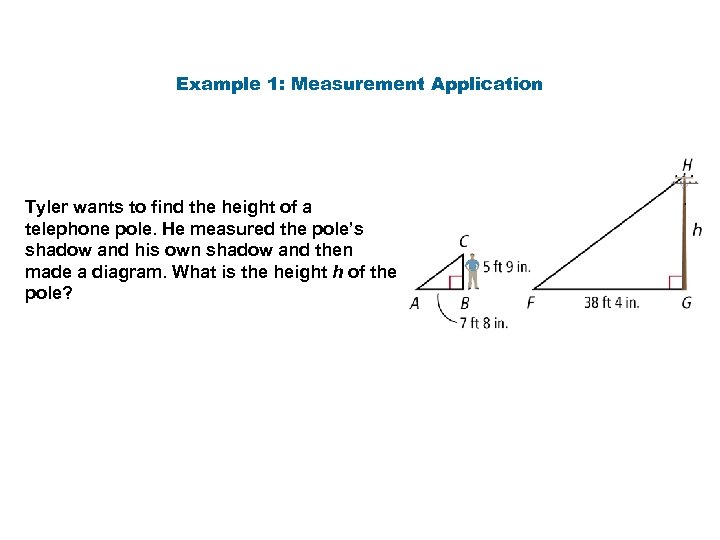Example 1: Measurement Application Tyler wants to find the height of a telephone pole. He measured the pole’s shadow and his own shadow and then made a diagram. What is the height h of the pole?

Example 1 Continued Step 1 Convert the measurements to inches. AB = 7 ft 8 in. = (7 12) in. + 8 in. = 92 in. BC = 5 ft 9 in. = (5 12) in. + 9 in. = 69 in. FG = 38 ft 4 in. = (38 12) in. + 4 in. = 460 in. Step 2 Find similar triangles. Because the sun’s rays are parallel, A F. Therefore ∆ABC ~ ∆FGH by AA ~. Step 3 Find h. Corr. sides are proportional. Substitute 69 for BC, h for GH, 92 for AB, and 460 for FG. 92 h = 69 460 h = 345 Cross Products Prop. The height h of the pole is 345 inches, or 28 feet 9 inches.

Check It Out! Example 1 A student who is 5 ft 6 in. tall measured shadows to find the height LM of a flagpole. What is LM? Step 1 Convert the measurements to inches. GH = 5 ft 6 in. = (5 12) in. + 6 in. = 66 in. JH = 5 ft = (5 12) in. = 60 in. NM = 14 ft 2 in. = (14 12) in. + 2 in. = 170 in.

Step 2 Find similar triangles. Because the sun’s rays are parallel, L G. Therefore ∆JGH ~ ∆NLM by AA ~. Step 3 Find h. Corr. sides are proportional. Substitute 66 for BC, h for LM, 60 for JH, and 170 for MN. 60(h) = 66 170 h = 187 Cross Products Prop. Divide both sides by 60. The height of the flagpole is 187 in. , or 15 ft. 7 in.

Example 3: Making a Scale Drawing Lady Liberty holds a tablet in her left hand. The tablet is 7. 19 m long and 4. 14 m wide. If you made a scale drawing using the scale 1 cm: 0. 75 m, what would be the dimensions to the nearest tenth?

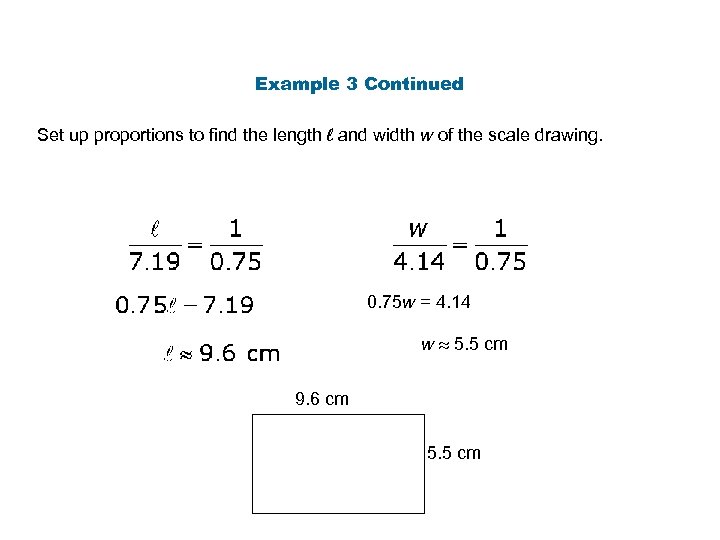Example 3 Continued Set up proportions to find the length l and width w of the scale drawing. 0. 75 w = 4. 14 w 5. 5 cm 9. 6 cm 5. 5 cm

Check It Out! Example 3 The rectangular central chamber of the Lincoln Memorial is 74 ft long and 60 ft wide. Make a scale drawing of the floor of the chamber using a scale of 1 in. : 20 ft.

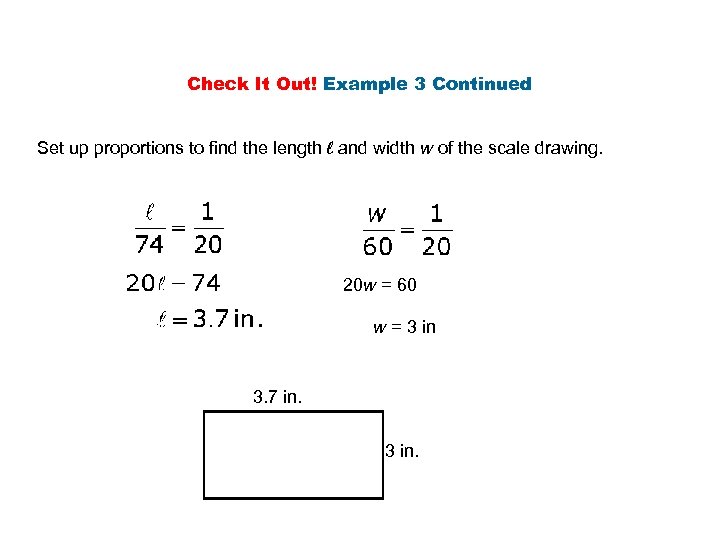Check It Out! Example 3 Continued Set up proportions to find the length l and width w of the scale drawing. 20 w = 60 w = 3 in 3. 7 in. 3 in.

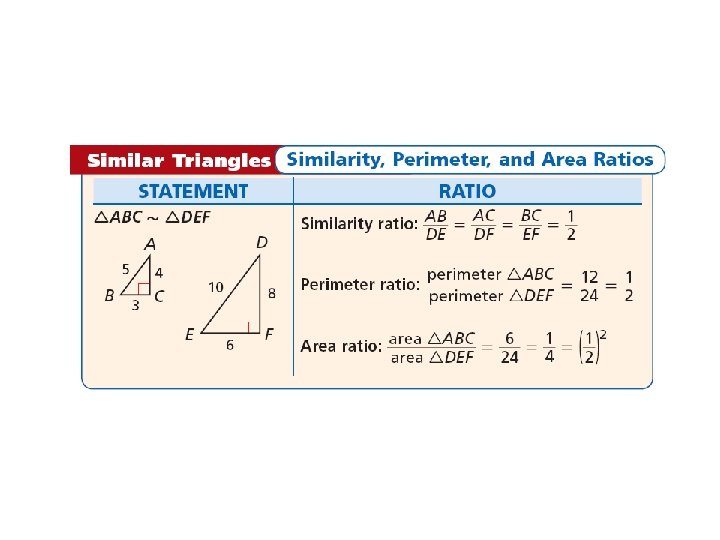
Example 4: Using Ratios to Find Perimeters and Areas Given that ∆LMN: ∆QRT, find the perimeter P and area A of ∆QRS. The similarity ratio of ∆LMN to ∆QRS is By the Proportional Perimeters and Areas Theorem, the ratio of the triangles’ perimeters is also , and the ratio of the triangles’ areas is

Example 4 Continued Perimeter 13 P = 36(9. 1) P = 25. 2 Area 132 A = (9. 1)2(60) A = 29. 4 cm 2 The perimeter of ∆QRS is 25. 2 cm, and the area is 29. 4 cm 2.

Check It Out! Example 4 ∆ABC ~ ∆DEF, BC = 4 mm, and EF = 12 mm. If P = 42 mm and A = 96 mm 2 for ∆DEF, find the perimeter and area of ∆ABC. Perimeter 12 P = 42(4) Area 122 A = (4)2(96) P = 14 mm The perimeter of ∆ABC is 14 mm, and the area is 10. 7 mm 2.

Lesson Quiz: Part I 1. Maria is 4 ft 2 in. tall. To find the height of a flagpole, she measured her shadow and the pole’s shadow. What is the height h of the flagpole? 25 ft 2. A blueprint for Latisha’s bedroom uses a scale of 1 in. : 4 ft. Her bedroom on the blueprint is 3 in. long. How long is the actual room? 12 ft

Lesson Quiz: Part II 3. ∆ABC ~ ∆DEF. Find the perimeter and area of ∆ABC. P = 27 in. , A = 31. 5 in 2

Ch 6. 3 Activity pg 298 • Draw ⍍DEF with m∠D = 35, m∠ F = 80, and DF = 4 cm • Draw ⍍RST with m∠R = 35, m∠ S = 80, and ST = 7 cm • Measure EF, ED, RS, RT • Calculate the ratios FD, EF, and ED ST RS RT 1. What can you conclude about all of the ratios? 2. What are the minimum requirements for two triangles to be similar?

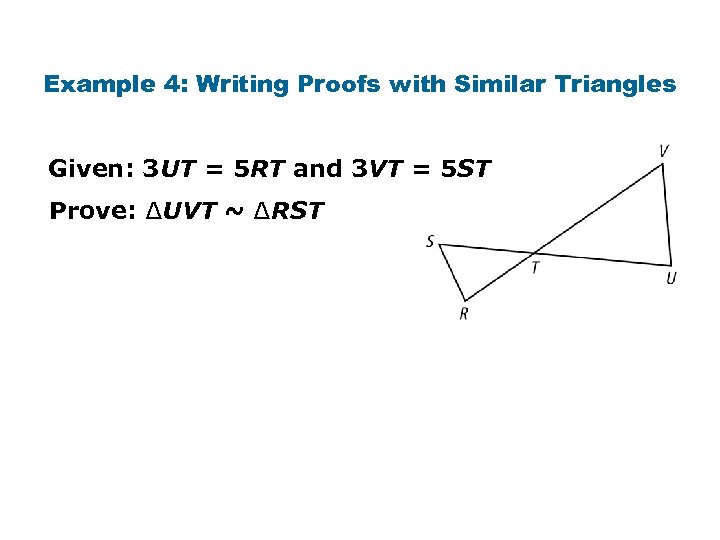Example 4: Writing Proofs with Similar Triangles Given: 3 UT = 5 RT and 3 VT = 5 ST Prove: ∆UVT ~ ∆RST

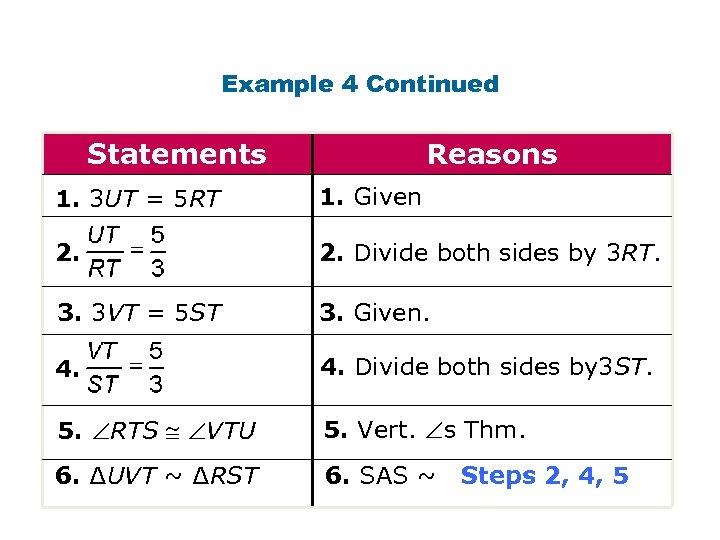Example 4 Continued Statements Reasons 1. 3 UT = 5 RT 1. Given 2. Divide both sides by 3 RT. 3. 3 VT = 5 ST 3. Given. 4. Divide both sides by 3 ST. 5. RTS VTU 5. Vert. s Thm. 6. ∆UVT ~ ∆RST 6. SAS ~ Steps 2, 4, 5

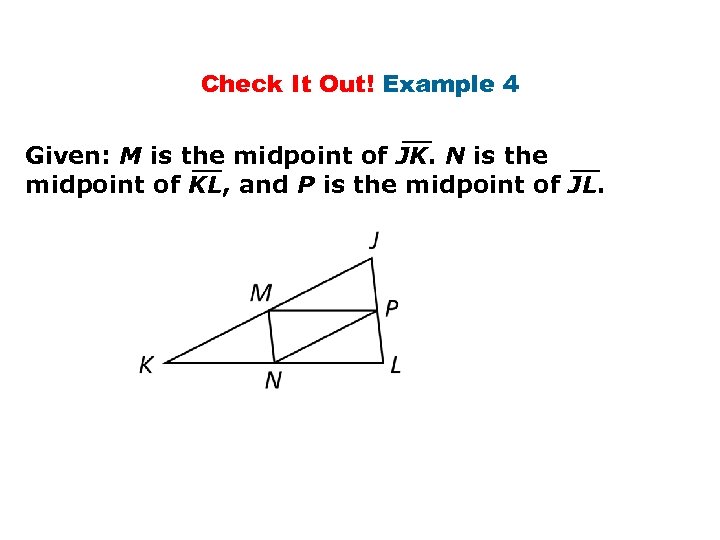Check It Out! Example 4 Given: M is the midpoint of JK. N is the midpoint of KL, and P is the midpoint of JL.

Check It Out! Example 4 Continued Statements Reasons 1. M is the mdpt. of JK, N is the mdpt. of KL, and P is the mdpt. of JL. 1. Given 2. ∆ Midsegs. Thm 3. Div. Prop. of =. 4. ∆JKL ~ ∆NPM 4. SSS ~ Step 3