b0b15804baa046c143172da269d7b33d.ppt
- Количество слайдов: 45
 W HY ARE NUCLEI PROLATE: Deformation is a collective effect Pavel Str ánský Alejandro Frank Roelof Bijker Instituto de Ciencias Nucleares, Universidad Nacional Aut ónoma de M éxico XXXIV Symposium on Nuclear Physics, Cocoyoc, Mexico, 2011 7 th January 2011
W HY ARE NUCLEI PROLATE: Deformation is a collective effect Pavel Str ánský Alejandro Frank Roelof Bijker Instituto de Ciencias Nucleares, Universidad Nacional Aut ónoma de M éxico XXXIV Symposium on Nuclear Physics, Cocoyoc, Mexico, 2011 7 th January 2011
 W HY ARE NUCLEI PROLATE: Deformation is a collective effect 1. Single particle x collective approaches 2. Deformed liquid drop model Binding energy (Mass formula) Quadrupole deformation Shape stabilization: Shell corrections 3. Results Prolate-oblate energy difference for experimental data of electric quadrupole moments and B(E 2) transitions
W HY ARE NUCLEI PROLATE: Deformation is a collective effect 1. Single particle x collective approaches 2. Deformed liquid drop model Binding energy (Mass formula) Quadrupole deformation Shape stabilization: Shell corrections 3. Results Prolate-oblate energy difference for experimental data of electric quadrupole moments and B(E 2) transitions
 1. Single-particle x collective approaches
1. Single-particle x collective approaches
 1. Single-particle models Single-particle description Collective • Nillson-like models • deformed liquid excitations drop models Stable ground-state configuration Minimization of the total sum of the lowest-lying occupied one-particle energies with respect to the size of the potential deformation Minimization of the equilibrium energy with respect to the size of the shape deformation
1. Single-particle models Single-particle description Collective • Nillson-like models • deformed liquid excitations drop models Stable ground-state configuration Minimization of the total sum of the lowest-lying occupied one-particle energies with respect to the size of the potential deformation Minimization of the equilibrium energy with respect to the size of the shape deformation
 1. Single-particle models Chocolate-box model • a demonstration of the single-particle approach y x=y x z Spectrum: Volume conservation: xyz = const. deformation parameter
1. Single-particle models Chocolate-box model • a demonstration of the single-particle approach y x=y x z Spectrum: Volume conservation: xyz = const. deformation parameter
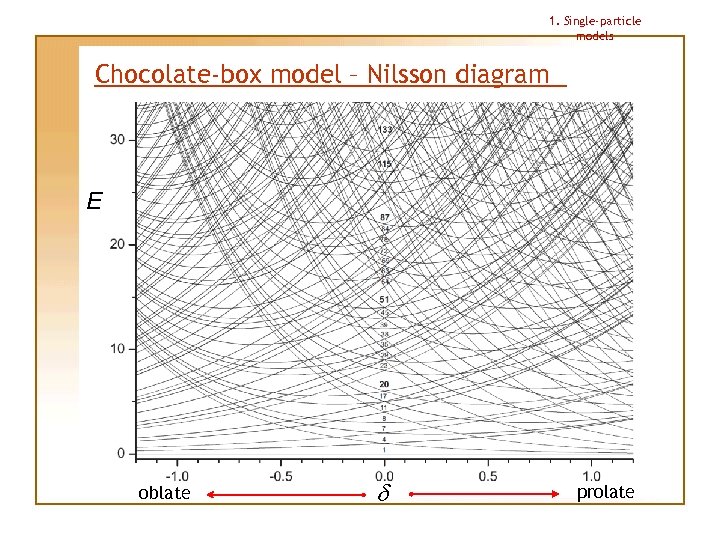 1. Single-particle models Chocolate-box model – Nilsson diagram E oblate d prolate
1. Single-particle models Chocolate-box model – Nilsson diagram E oblate d prolate
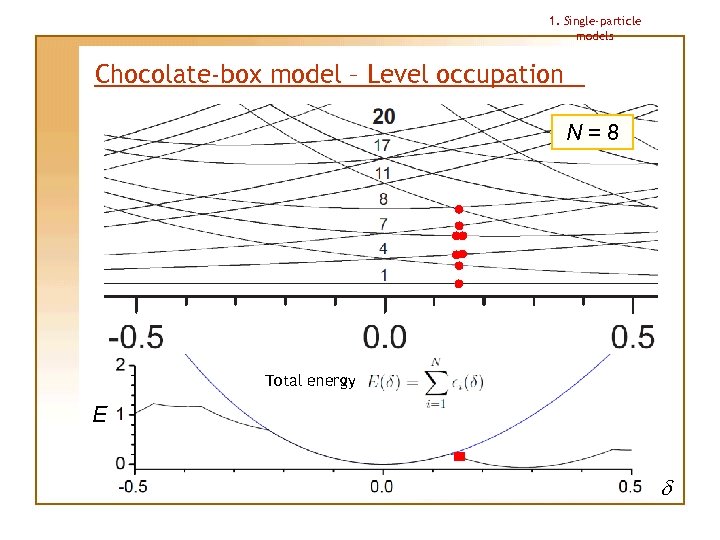
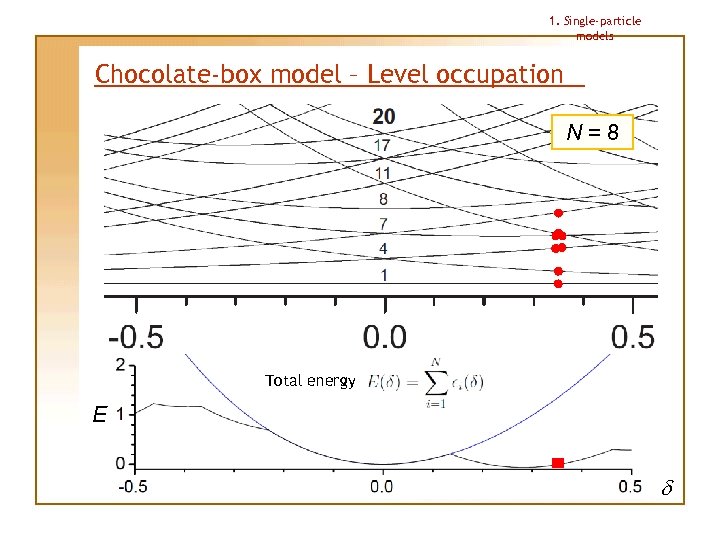
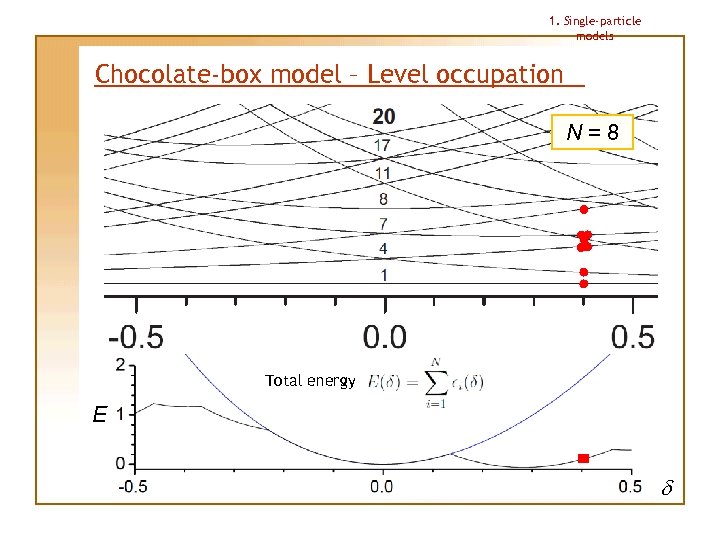
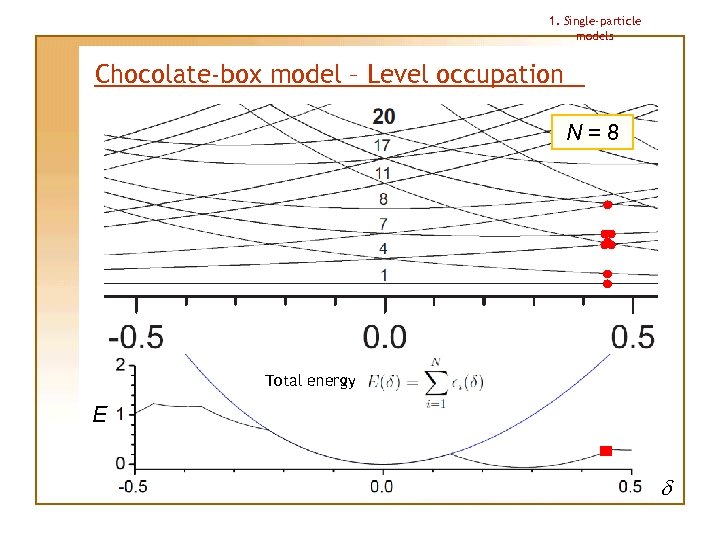
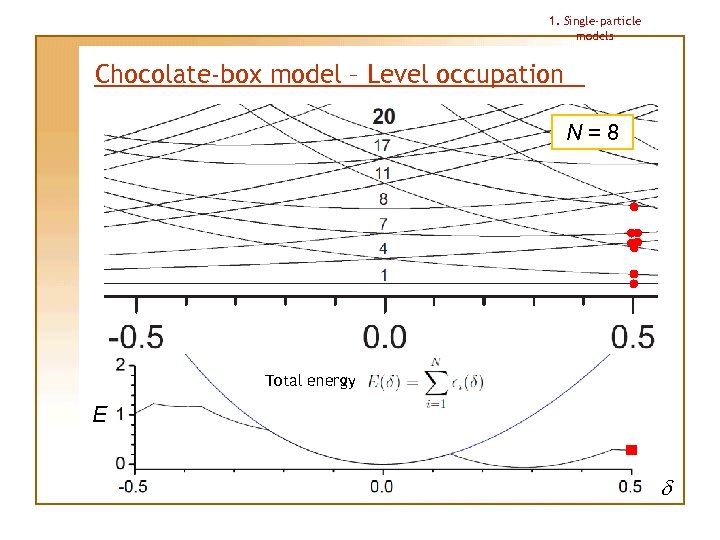
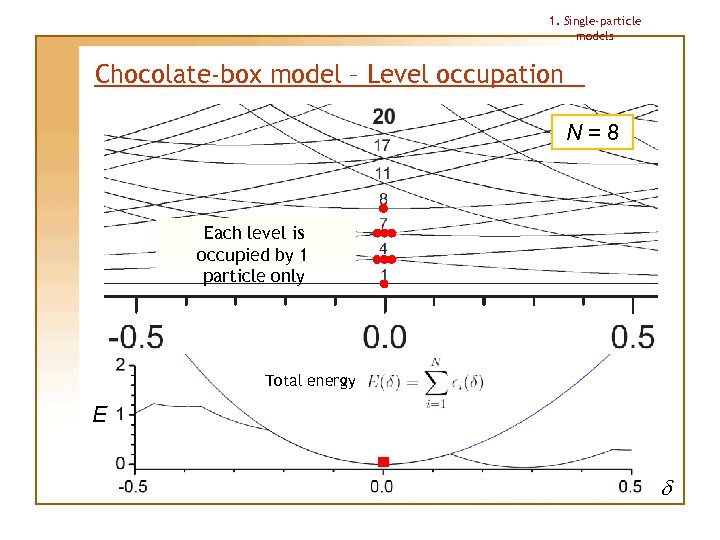 1. Single-particle models Chocolate-box model – Level occupation N=8 Each level is occupied by 1 particle only Total energy E d
1. Single-particle models Chocolate-box model – Level occupation N=8 Each level is occupied by 1 particle only Total energy E d
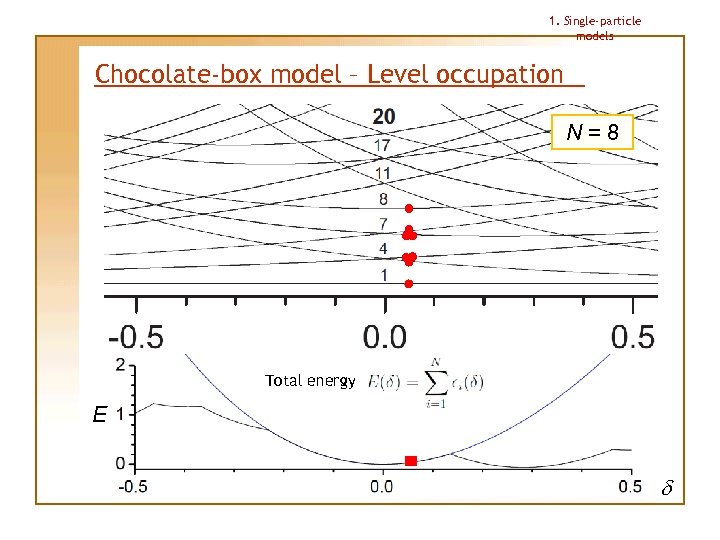 1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
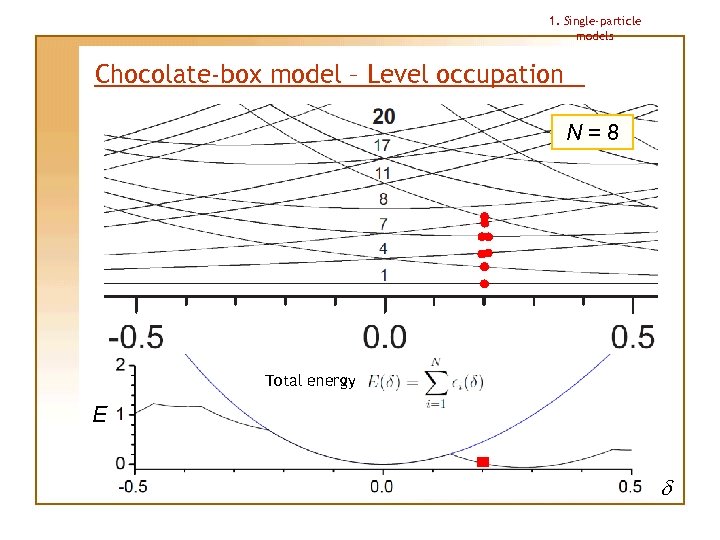
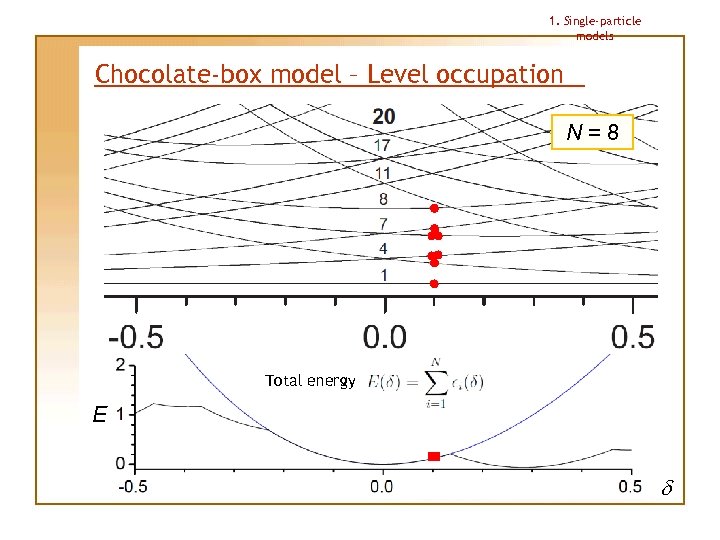 1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
 1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
 1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
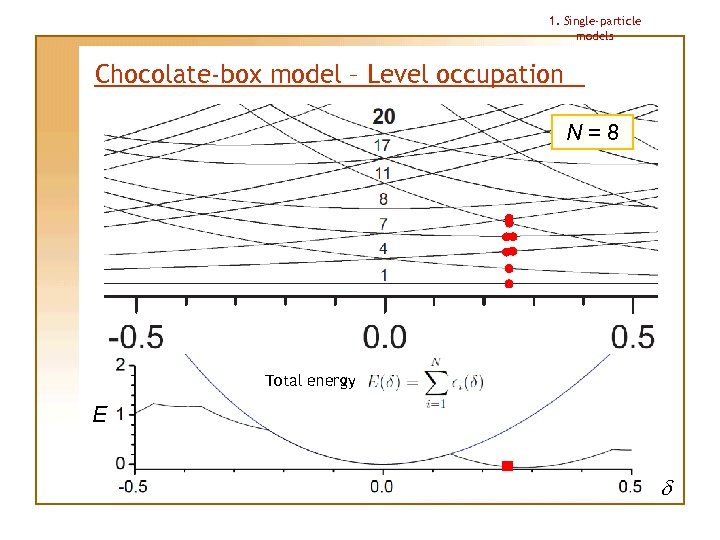 1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
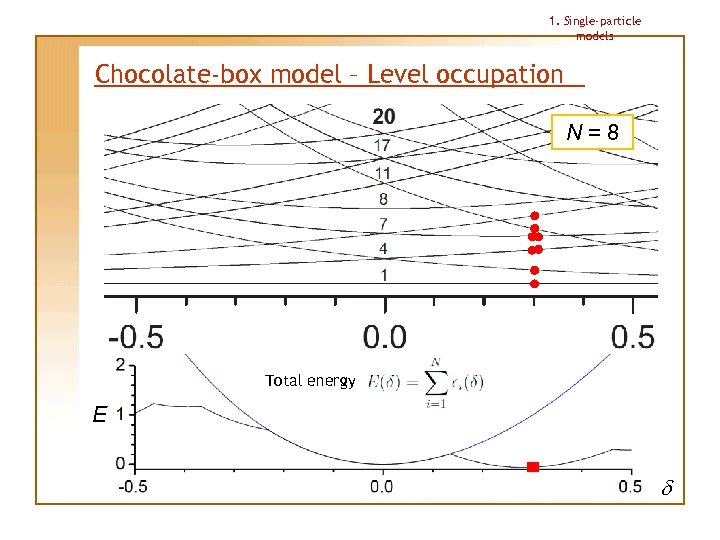 1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
 1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
 1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
 1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
 1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
1. Single-particle models Chocolate-box model – Level occupation N=8 Total energy E d
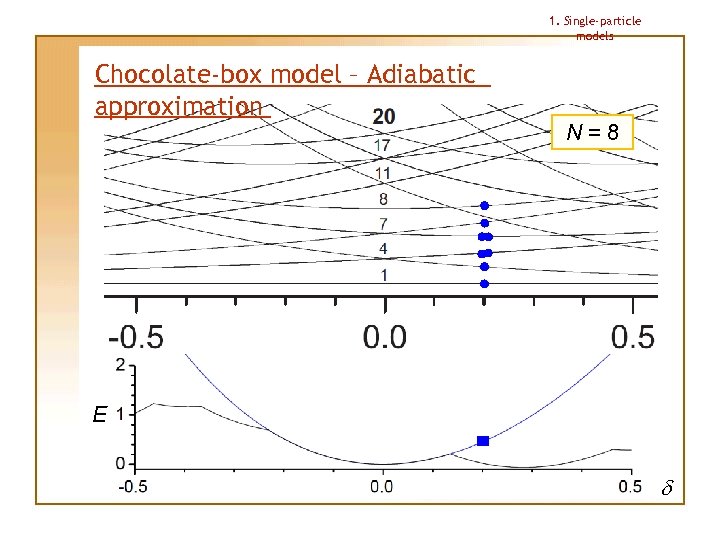
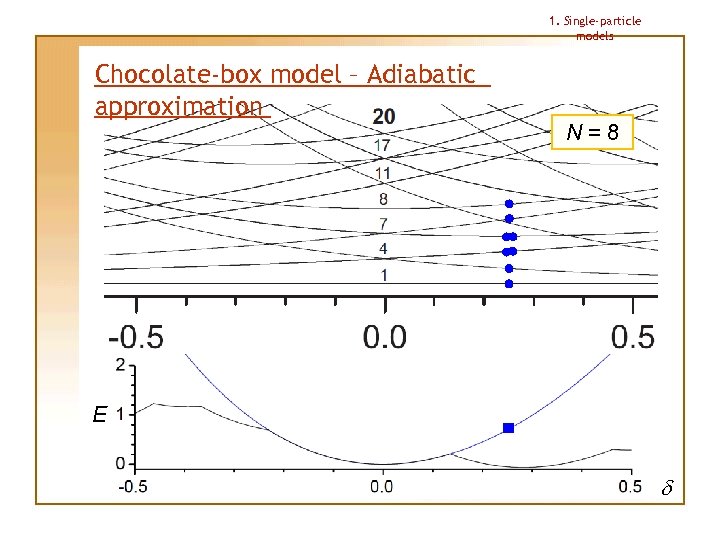
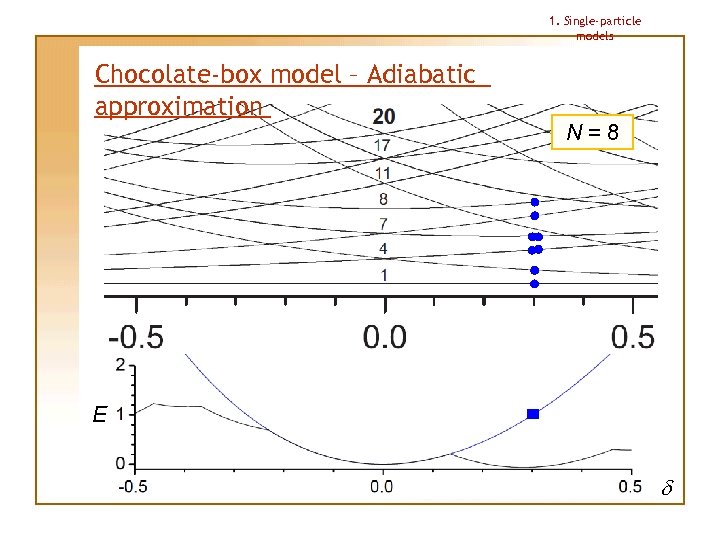
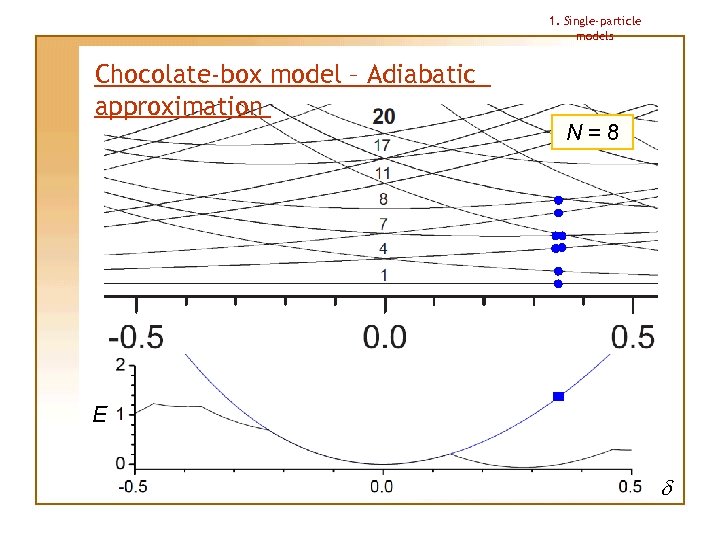
 1. Single-particle models Chocolate-box model – Adiabatic approximation This approximation allows us to determine the shape for a given particle number N uniquely Procedure: 1. Lowest single-particle levels are occupied for small deformation |d| 2. Deformation is then changed “adiabatically”, making the particles stay on the same levels as in the beginning, no matter if there happens to appear another level with lower energy 3. Total energy under this approximation has always 1 (spherical) or 2 (deformed) minima; the deeper minimum determines the shape
1. Single-particle models Chocolate-box model – Adiabatic approximation This approximation allows us to determine the shape for a given particle number N uniquely Procedure: 1. Lowest single-particle levels are occupied for small deformation |d| 2. Deformation is then changed “adiabatically”, making the particles stay on the same levels as in the beginning, no matter if there happens to appear another level with lower energy 3. Total energy under this approximation has always 1 (spherical) or 2 (deformed) minima; the deeper minimum determines the shape
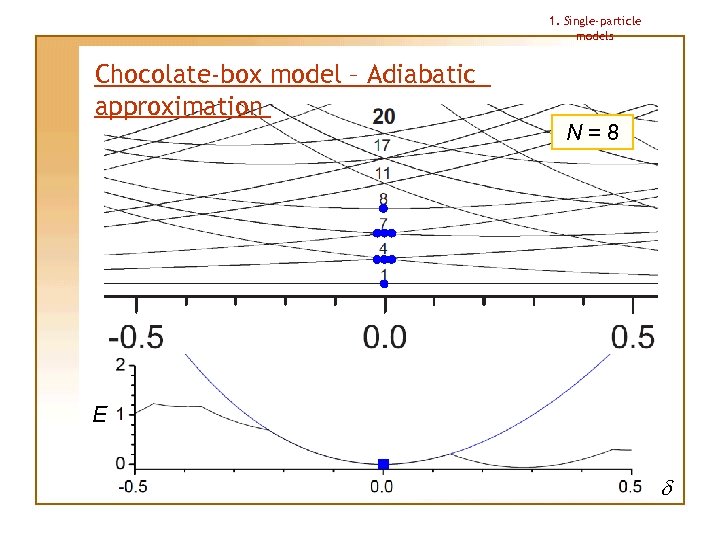 1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
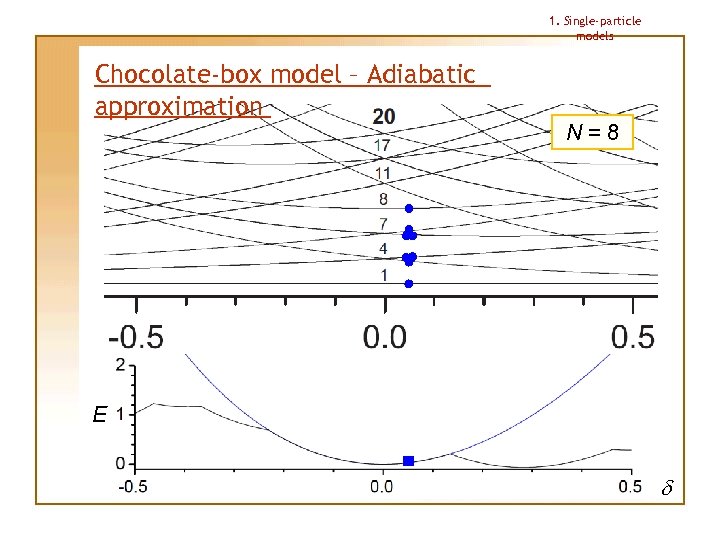 1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
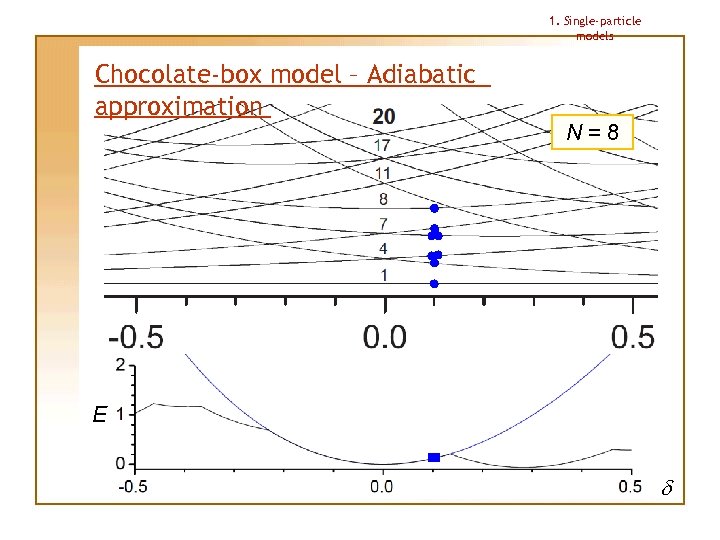 1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
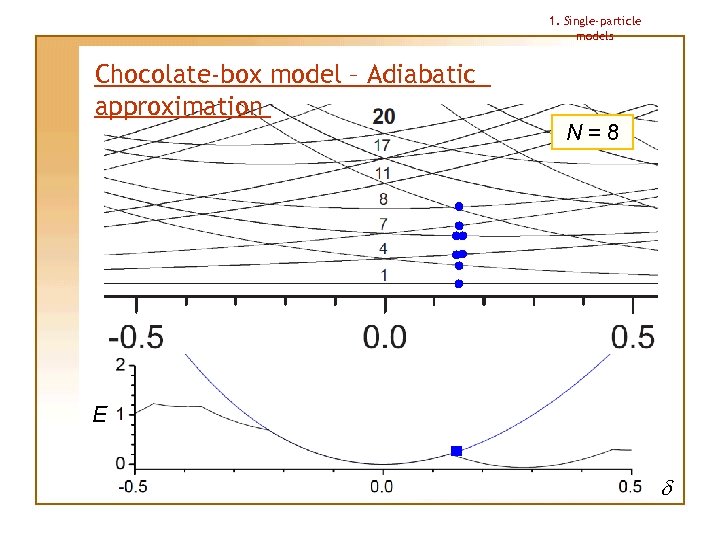 1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
 1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
 1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
 1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
 1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
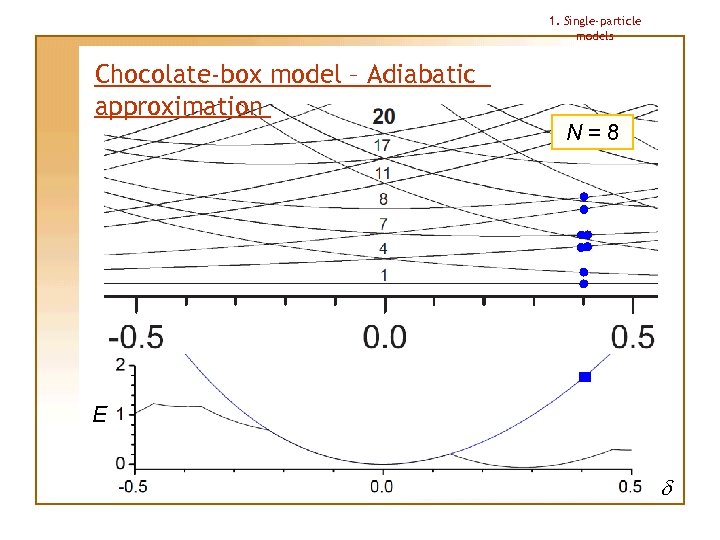 1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
1. Single-particle models Chocolate-box model – Adiabatic approximation N=8 E d
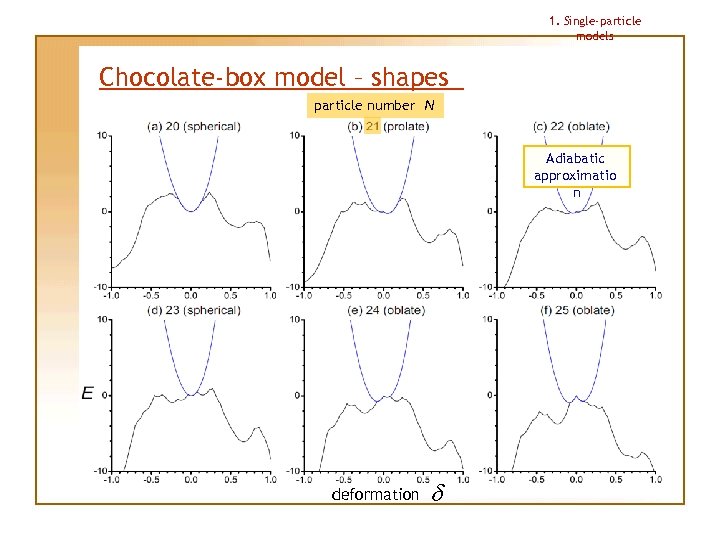 1. Single-particle models Chocolate-box model – shapes particle number N Adiabatic approximatio n deformation d
1. Single-particle models Chocolate-box model – shapes particle number N Adiabatic approximatio n deformation d
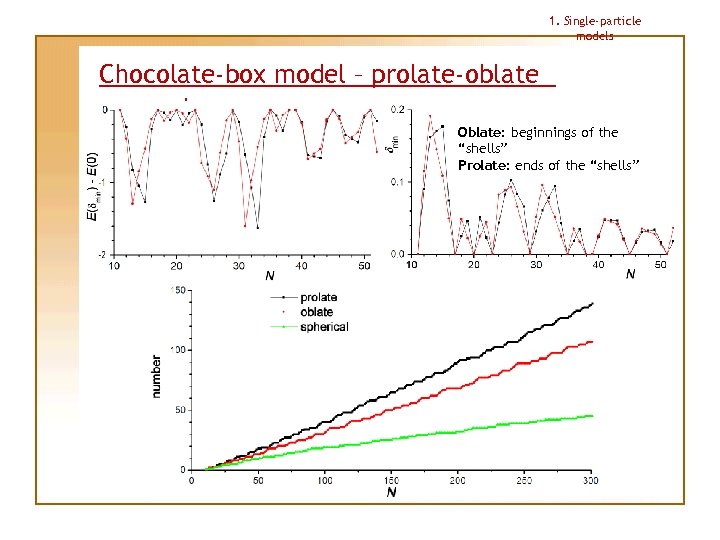 1. Single-particle models Chocolate-box model – prolate-oblate assymetry Oblate: beginnings of the “shells” Prolate: ends of the “shells”
1. Single-particle models Chocolate-box model – prolate-oblate assymetry Oblate: beginnings of the “shells” Prolate: ends of the “shells”
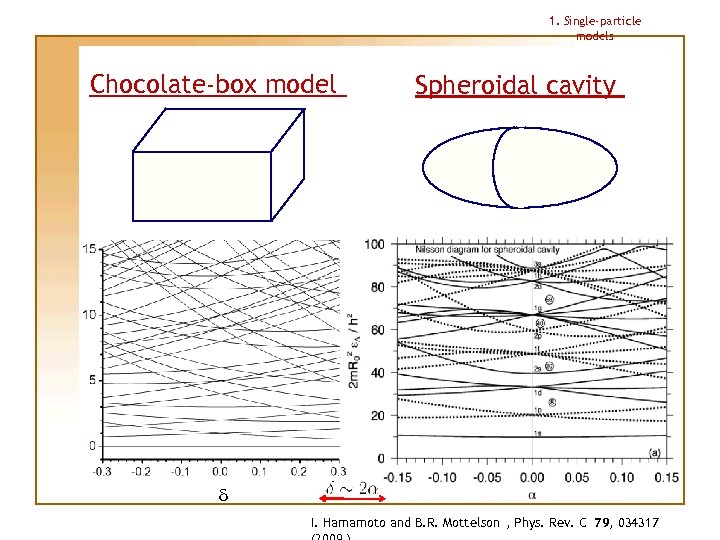 1. Single-particle models Chocolate-box model Spheroidal cavity d I. Hamamoto and B. R. Mottelson , Phys. Rev. C 79, 034317
1. Single-particle models Chocolate-box model Spheroidal cavity d I. Hamamoto and B. R. Mottelson , Phys. Rev. C 79, 034317
 2. Deformed liquid drop model
2. Deformed liquid drop model
 2. Liquid drop model Total mass/energy (Weizs äcker formula) binding energy volume energy A=N+Z surface energy microscopic corrections (shell effects, pairing) Coulomb energy curvature energy, surface and volume redistribution energy… Adjustable constants: Shape functions: W. D. Myers, W. J. Swiatecki, Nucl. Phys. 81, 1 (1966 )
2. Liquid drop model Total mass/energy (Weizs äcker formula) binding energy volume energy A=N+Z surface energy microscopic corrections (shell effects, pairing) Coulomb energy curvature energy, surface and volume redistribution energy… Adjustable constants: Shape functions: W. D. Myers, W. J. Swiatecki, Nucl. Phys. 81, 1 (1966 )
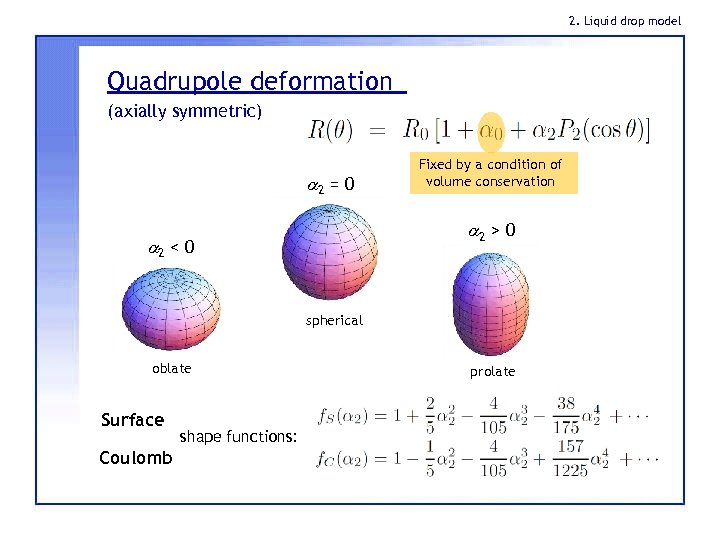 2. Liquid drop model Quadrupole deformation (axially symmetric) a 2 = 0 Fixed by a condition of volume conservation a 2 > 0 a 2 < 0 spherical oblate Surface Coulomb shape functions: prolate
2. Liquid drop model Quadrupole deformation (axially symmetric) a 2 = 0 Fixed by a condition of volume conservation a 2 > 0 a 2 < 0 spherical oblate Surface Coulomb shape functions: prolate
 2. Liquid drop model Quadrupole deformation – shape functions Surface Coulomb shape functions:
2. Liquid drop model Quadrupole deformation – shape functions Surface Coulomb shape functions:
 2. Liquid drop model Quadrupole deformation – shape functions Symmetric with respect to the sign of Surface a 2 shape functions: Coulomb Negative for a 2 < 0 – prolate shape has always lower energy Values of the coefficients Deformation parameter
2. Liquid drop model Quadrupole deformation – shape functions Symmetric with respect to the sign of Surface a 2 shape functions: Coulomb Negative for a 2 < 0 – prolate shape has always lower energy Values of the coefficients Deformation parameter
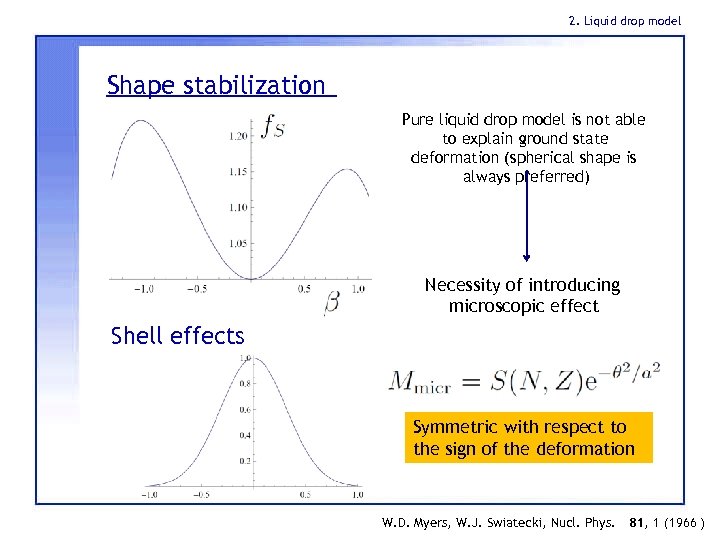 2. Liquid drop model Shape stabilization Pure liquid drop model is not able to explain ground state deformation (spherical shape is always preferred) Necessity of introducing microscopic effect Shell effects Symmetric with respect to the sign of the deformation W. D. Myers, W. J. Swiatecki, Nucl. Phys. 81, 1 (1966 )
2. Liquid drop model Shape stabilization Pure liquid drop model is not able to explain ground state deformation (spherical shape is always preferred) Necessity of introducing microscopic effect Shell effects Symmetric with respect to the sign of the deformation W. D. Myers, W. J. Swiatecki, Nucl. Phys. 81, 1 (1966 )
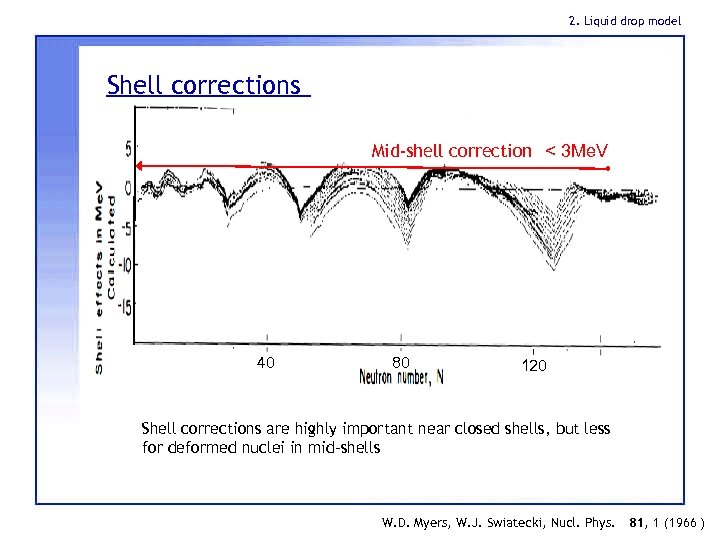 2. Liquid drop model Shell corrections Mid-shell correction < 3 Me. V 40 80 120 Shell corrections are highly important near closed shells, but less for deformed nuclei in mid-shells W. D. Myers, W. J. Swiatecki, Nucl. Phys. 81, 1 (1966 )
2. Liquid drop model Shell corrections Mid-shell correction < 3 Me. V 40 80 120 Shell corrections are highly important near closed shells, but less for deformed nuclei in mid-shells W. D. Myers, W. J. Swiatecki, Nucl. Phys. 81, 1 (1966 )
 3. Prolate-oblate energy difference from experiments
3. Prolate-oblate energy difference from experiments
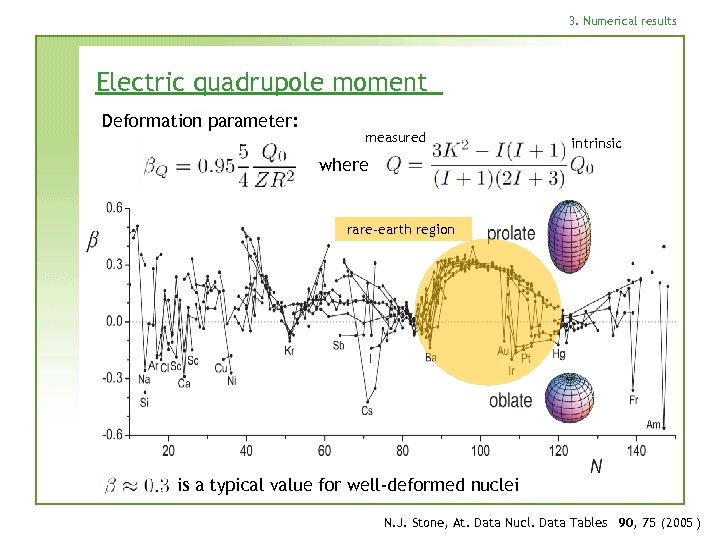 3. Numerical results Electric quadrupole moment Deformation parameter: measured intrinsic where rare-earth region is a typical value for well-deformed nuclei N. J. Stone, At. Data Nucl. Data Tables 90, 75 (2005 )
3. Numerical results Electric quadrupole moment Deformation parameter: measured intrinsic where rare-earth region is a typical value for well-deformed nuclei N. J. Stone, At. Data Nucl. Data Tables 90, 75 (2005 )
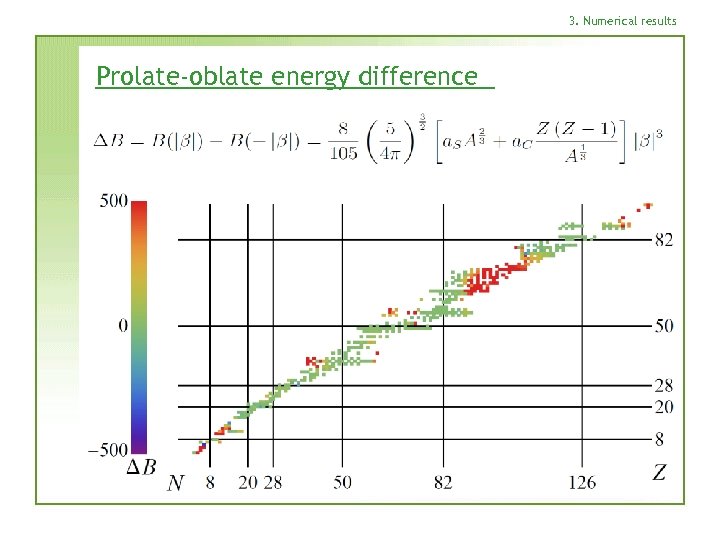 3. Numerical results Prolate-oblate energy difference
3. Numerical results Prolate-oblate energy difference
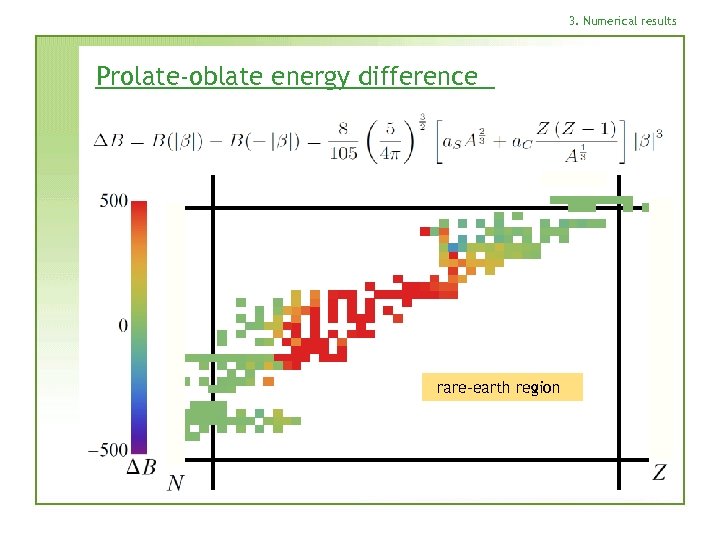 3. Numerical results Prolate-oblate energy difference rare-earth region
3. Numerical results Prolate-oblate energy difference rare-earth region
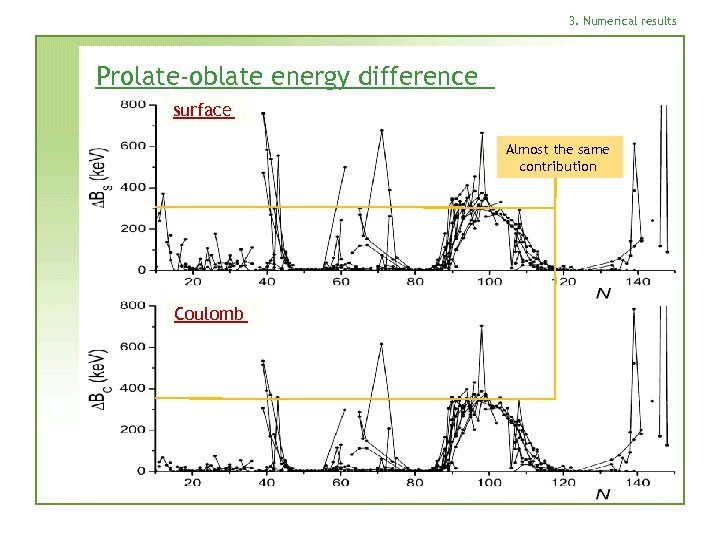 3. Numerical results Prolate-oblate energy difference surface Almost the same contribution Coulomb
3. Numerical results Prolate-oblate energy difference surface Almost the same contribution Coulomb
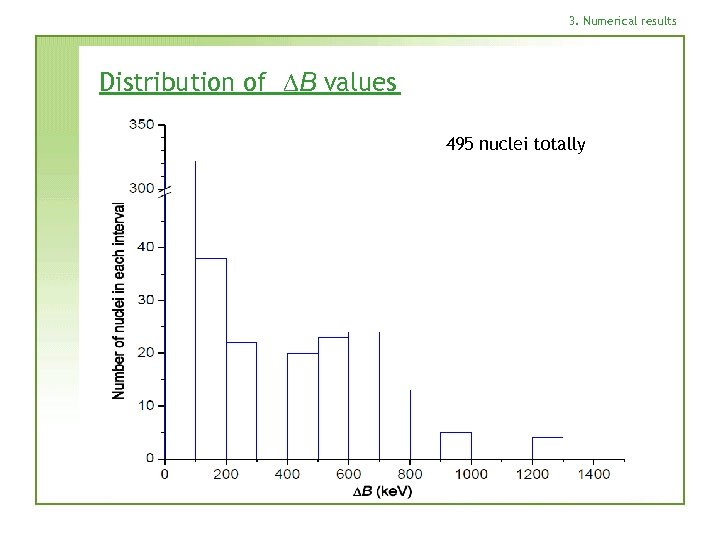 3. Numerical results Distribution of DB values 495 nuclei totally
3. Numerical results Distribution of DB values 495 nuclei totally
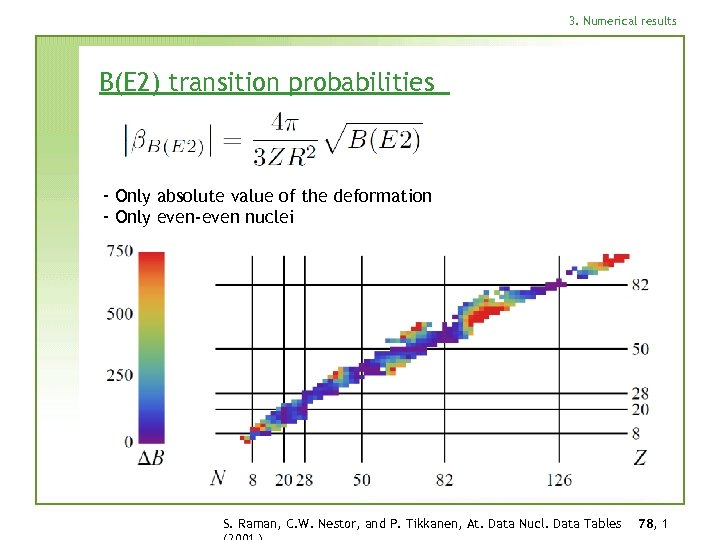 3. Numerical results B(E 2) transition probabilities - Only absolute value of the deformation - Only even-even nuclei S. Raman, C. W. Nestor, and P. Tikkanen, At. Data Nucl. Data Tables 78, 1
3. Numerical results B(E 2) transition probabilities - Only absolute value of the deformation - Only even-even nuclei S. Raman, C. W. Nestor, and P. Tikkanen, At. Data Nucl. Data Tables 78, 1
 Last slid e Conclusions • • • Predominance of prolate states can be explained by a simple deformed liquid drop model. This approach is robust with a transparent physical understanding, in contrast with single particle studies that require fine-tunning procedures and are strongly model dependent. Prolate-oblate energy difference of the order of DB = 500 ke. V is high enough to be considered as non-negligible (for comparison, first 2+ excited state for well-deformed even-even nuclei is typically of the order of 100 ke. V). Microscopic shell effects are necessary to stabilize deformed shape, but in most cases the prolate-oblate asymmetry in energy they give is not strong enough to compete with collective effects. Thank you for your attention
Last slid e Conclusions • • • Predominance of prolate states can be explained by a simple deformed liquid drop model. This approach is robust with a transparent physical understanding, in contrast with single particle studies that require fine-tunning procedures and are strongly model dependent. Prolate-oblate energy difference of the order of DB = 500 ke. V is high enough to be considered as non-negligible (for comparison, first 2+ excited state for well-deformed even-even nuclei is typically of the order of 100 ke. V). Microscopic shell effects are necessary to stabilize deformed shape, but in most cases the prolate-oblate asymmetry in energy they give is not strong enough to compete with collective effects. Thank you for your attention


