Взаимоотношения хищника и жертвы Лекции 9 и 10

Взаимоотношения хищника и жертвы Лекции 9 и 10

Хищничество n Типичное хищничество встречается тогда, когда одно животное (хищник) ловит, убивает и поедает другое, менее удачливое животное (жертву). Для обсуждения взаимодействий популяций в более общем виде нам необходимо и более широкое определение хищничества, а именно: любое умерщвление с целью использования как пищи организмов одного вида организмами другого вида. 2

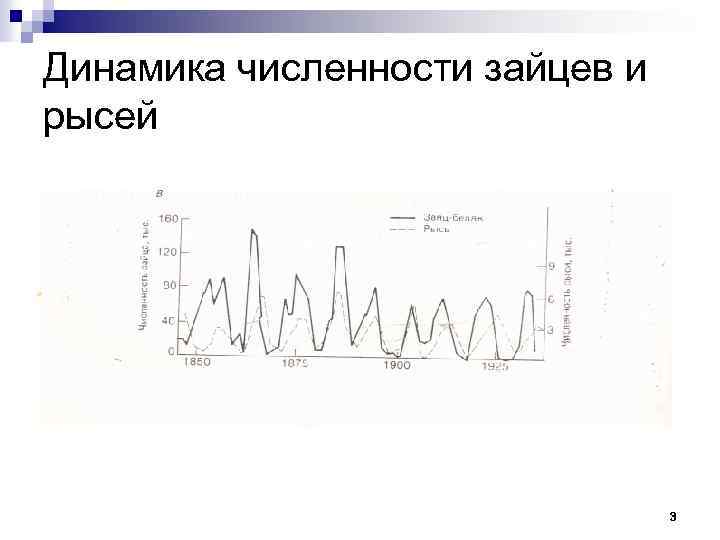Динамика численности зайцев и рысей 3

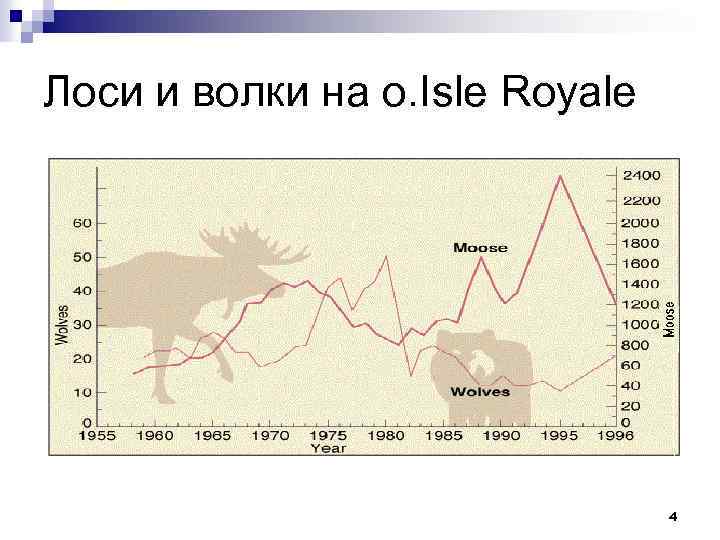Лоси и волки на о. Isle Royale 4

Эксперименты Г. Ф. Гаузе n В культуру с Paramecium caudatum он вводил особи Didinium nasutum небольших размеров хищника из простейших. Этот хищник прикрепляется к туфельке и затем проглатывает ее. 5

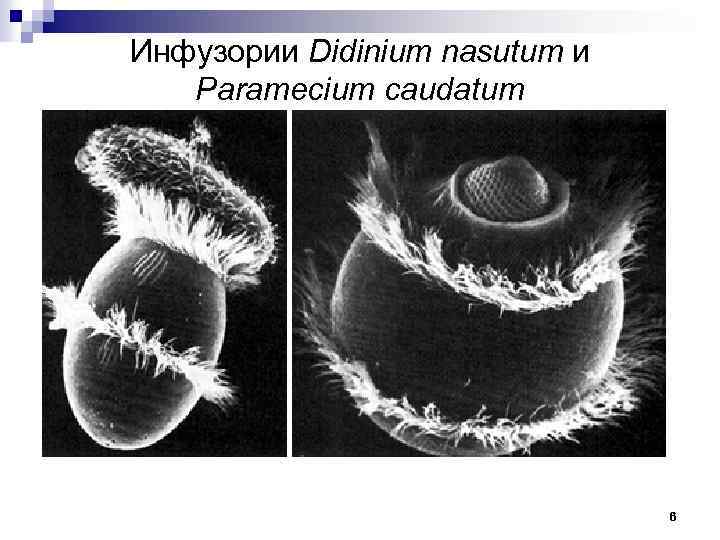Инфузории Didinium nasutum и Paramecium caudatum 6

7

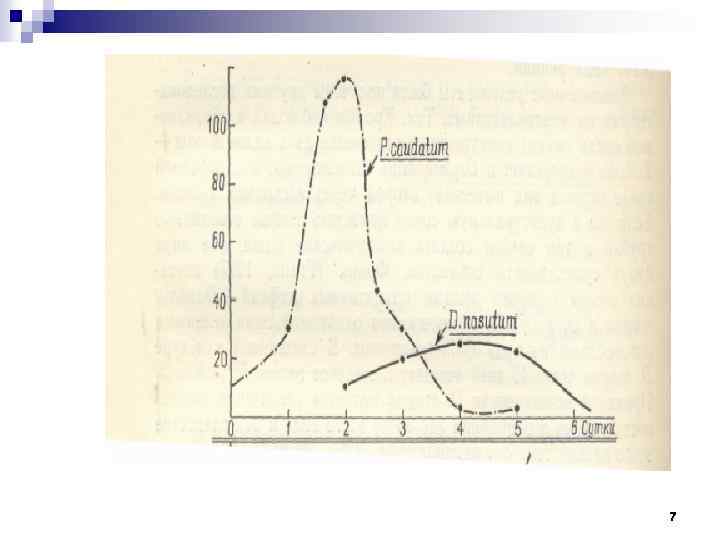
n Однажды введенный в культуру туфелек Didinium питается туфельками, размножается, и новые особи дидиния убивают туфелек до тех пор, пока все они не исчезнут из культуры. Тогда дидиний расплачивается за свое хищничество тем, что сам погибает от голода. 8

n Г. Ф. Гаузе нашел способ создать более стабильное взаимодействие двух видов путем использования культур с осадком на дне, где некоторые туфельки находят защиту от дидиния. 9

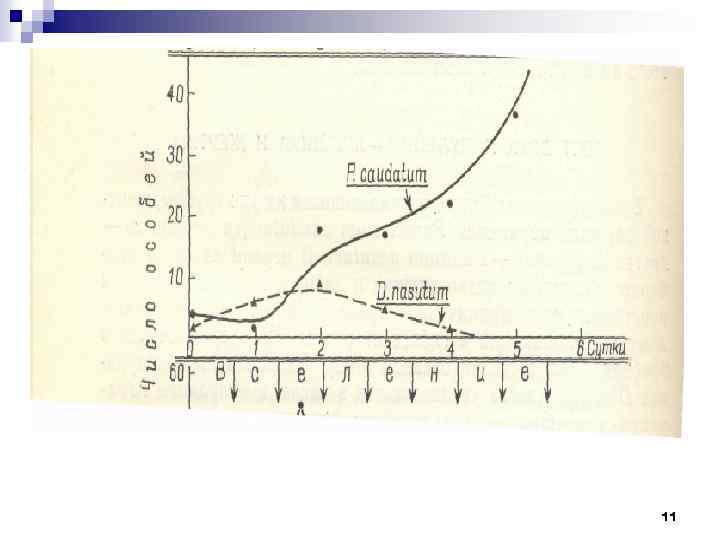
n Но стабильного взаимодействия в результате все же не получилось: дидиний размножается и уничтожает все туфельки, исключая те, которые спрятались, после чего дидиний погибают от голода, а туфельки начинают сигмоидальный рост в отсутствие хищника. 10

11

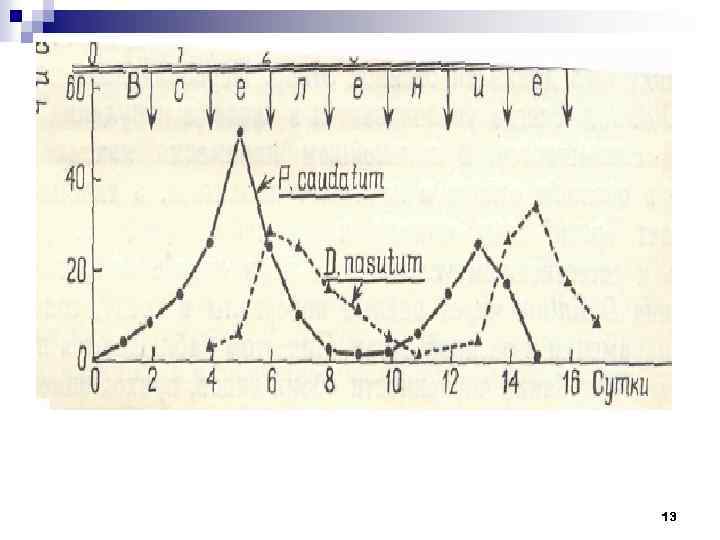
n Г. Ф. Гаузе удалось вызвать устойчивое взаимодействие (с заметными колебаниями в численности) только при периодическом добавлении и хищников и жертв в культуру. 12

13

Математические модели хищничества n Традиционные уравнения для описания взаимодействия хищника и жертвы предложили Лотка и Вольтерра. 14

n n n Популяция жертвы может расти с экспоненциальной скоростью (r 1 N 1 ) но при этом также будет терять особи, поедаемые хищником (—PN 1 N 2 ) Р — коэффициент хищничества, характеризующий отношение числа встреч к фактическому числу убитых жертв 15

n Популяция хищника нарастает со скоростью, которая прямо пропорциональна потреблению той же жертвы (a. PN 1 N 2 ) n а — коэффициент, относящий количество вновь рожденных хищников к числу съеденных жертв Предполагается, что хищники, умирают со скоростью, соразмерной с их плотностью (— d 2 N 2 ) n 16

А. Уравнения Лотки — Вольтерры 17

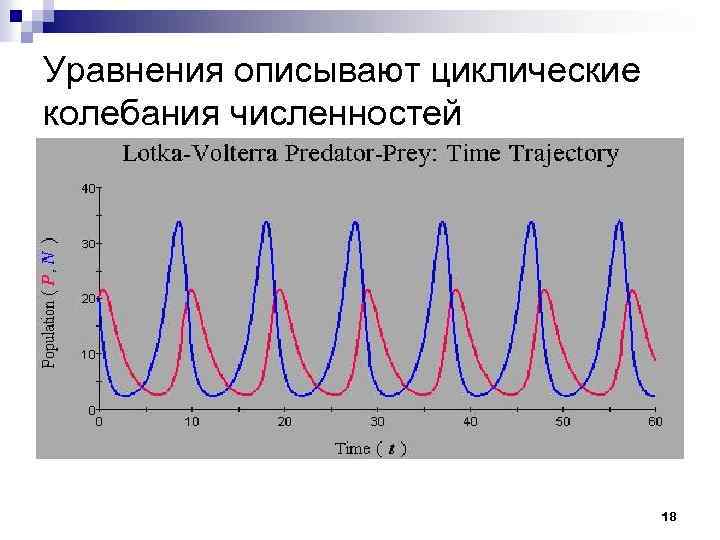Уравнения описывают циклические колебания численностей 18

Б. Допустимая численность n Более реалистично считать, что жертва имеет допустимую численность К 1, и придать уравнению жертвы логистическую форму. 19

20

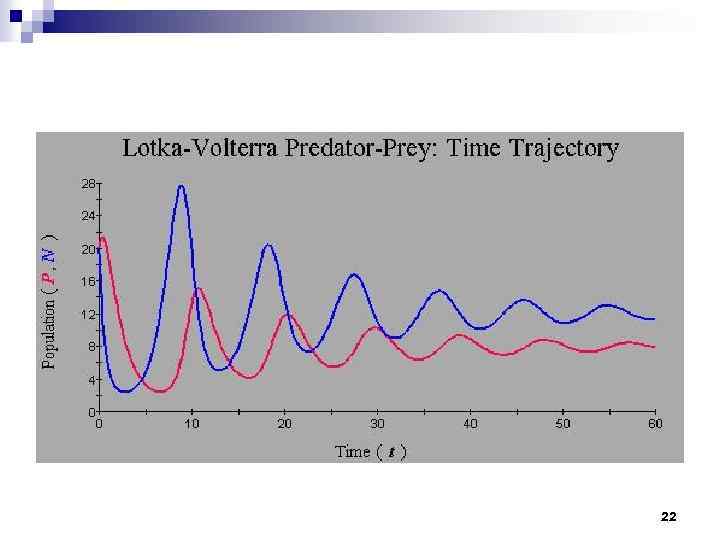
Если хищник также имеет допустимую численность (K 2 = b. N 1), предопределенную плотностью жертвы, то мы можем записать: 21

22

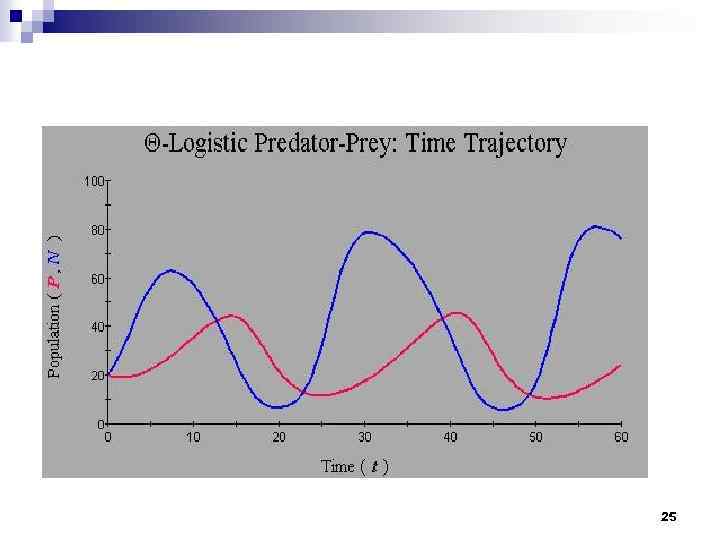
В. Насыщение хищника n Более реалистично считать, что существует предел количеству жертв, которые особь хищника в состоянии потребить, и отразить уменьшающееся потребление жертвы (в расчете на каждую жертву), как только этот предел приблизится к фактору насыщения С. 23

24

25

FIN 26