Лекция 7-8 биологи.pptx
- Количество слайдов: 120

Взаимодействия популяций
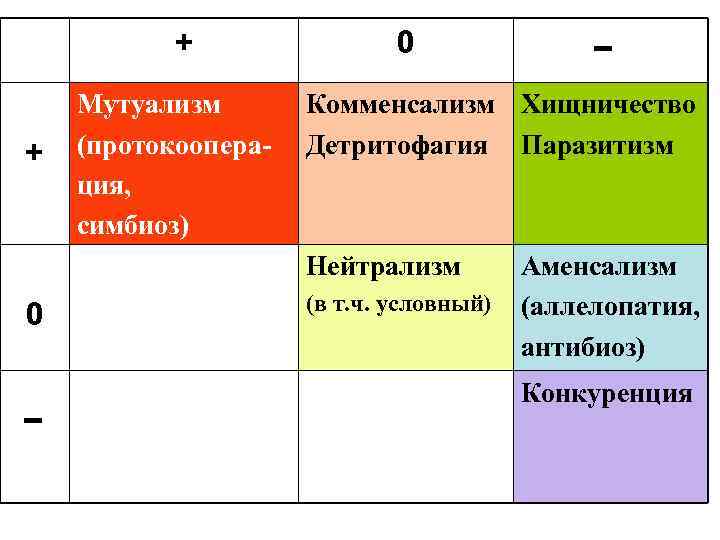
+ + Мутуализм (протокооперация, симбиоз) 0 Комменсализм Хищничество Детритофагия Паразитизм Нейтрализм 0 (в т. ч. условный) Аменсализм (аллелопатия, антибиоз) Конкуренция

В мире есть царь, Этот царь беспощаден – Голод названье ему (Н. Некрасов) Борьба за пищевые ресурсы – основа всех межпопуляционных взаимодействий

Основной критерий взаимодействия популяций: Если скорость изменения численности данной популяции меняется в присутствии популяции другого вида
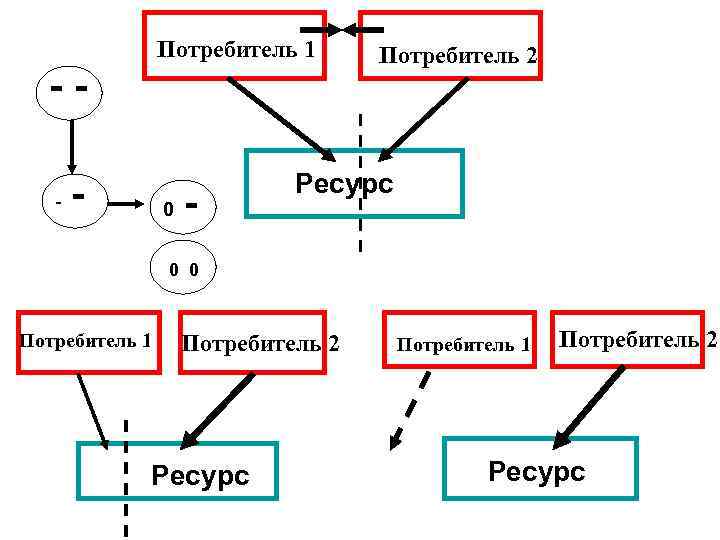
Потребитель 1 -- - 0 - Потребитель 2 Ресурс 0 0 Потребитель 1 Потребитель 2 Ресурс
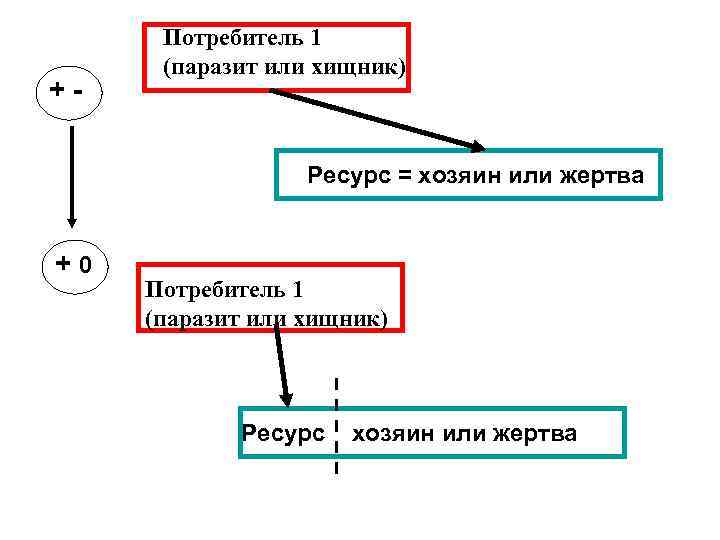
+- Потребитель 1 (паразит или хищник) Ресурс = хозяин или жертва +0 Потребитель 1 (паразит или хищник) Ресурс хозяин или жертва
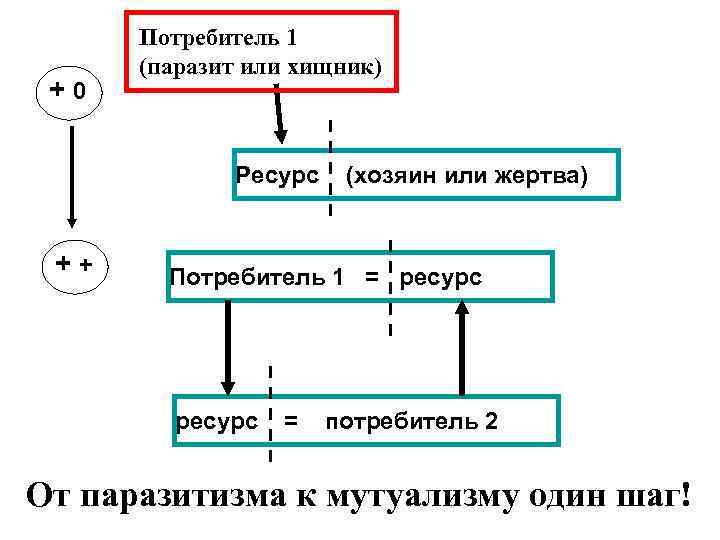
+0 Потребитель 1 (паразит или хищник) Ресурс ++ (хозяин или жертва) Потребитель 1 = ресурс = потребитель 2 От паразитизма к мутуализму один шаг!
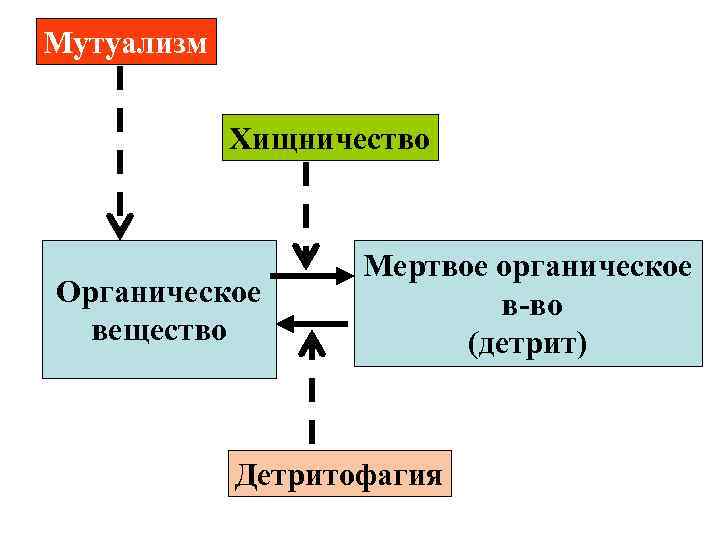
Мутуализм Хищничество Органическое вещество Мертвое органическое в-во (детрит) Детритофагия

Конкуренция И СОСУЩЕСТВОВАНИЕ Competition and coexistence
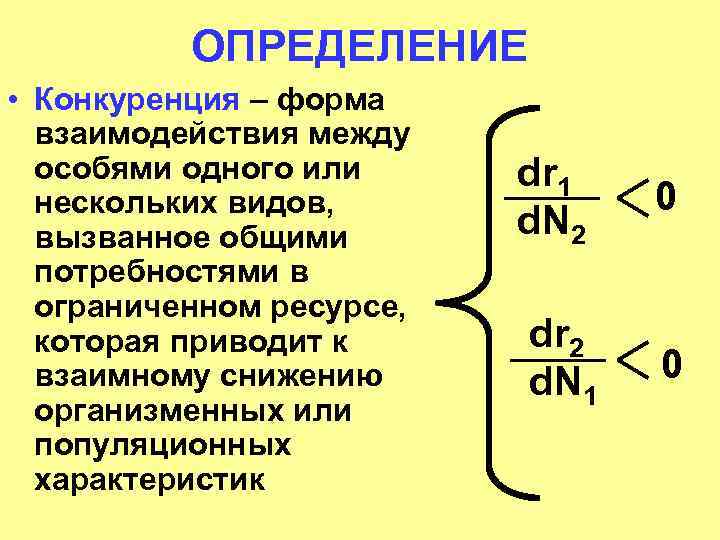
ОПРЕДЕЛЕНИЕ • Конкуренция – форма взаимодействия между особями одного или нескольких видов, вызванное общими потребностями в ограниченном ресурсе, которая приводит к взаимному снижению организменных или популяционных характеристик dr 1 d. N 2 0 dr 2 d. N 1 0

Виды конкуренции • Эксплуатационная; интерференционная; взаимная аллелопатия (антагонизм) • Внутри- и межвидовая • Симметричная и ассиметричная
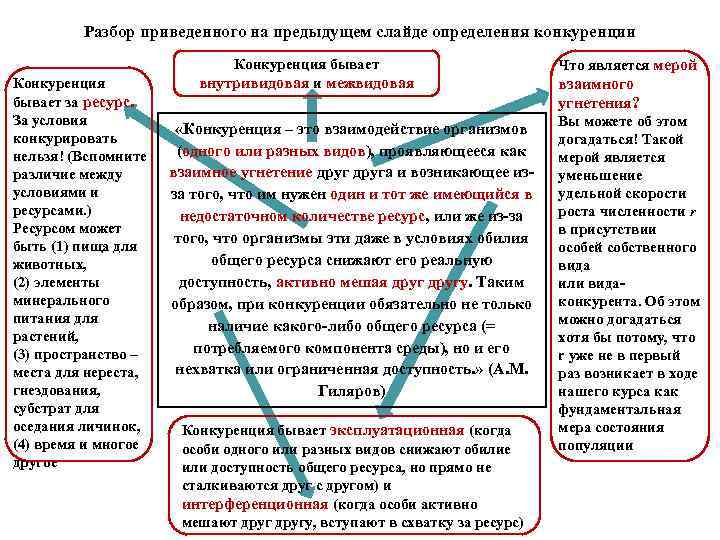
Разбор приведенного на предыдущем слайде определения конкуренции Конкуренция бывает за ресурс. За условия конкурировать нельзя! (Вспомните различие между условиями и ресурсами. ) Ресурсом может быть (1) пища для животных, (2) элементы минерального питания для растений, (3) пространство – места для нереста, гнездования, субстрат для оседания личинок, (4) время и многое другое Конкуренция бывает внутривидовая и межвидовая «Конкуренция – это взаимодействие организмов (одного или разных видов), проявляющееся как взаимное угнетение друга и возникающее изза того, что им нужен один и тот же имеющийся в недостаточном количестве ресурс, или же из-за того, что организмы эти даже в условиях обилия общего ресурса снижают его реальную доступность, активно мешая другу. Таким образом, при конкуренции обязательно не только наличие какого-либо общего ресурса (= потребляемого компонента среды), но и его нехватка или ограниченная доступность. » (А. М. Гиляров) Конкуренция бывает эксплуатационная (когда особи одного или разных видов снижают обилие или доступность общего ресурса, но прямо не сталкиваются друг с другом) и интерференционная (когда особи активно мешают другу, вступают в схватку за ресурс) Что является мерой взаимного угнетения? Вы можете об этом догадаться! Такой мерой является уменьшение удельной скорости роста численности r в присутствии особей собственного вида или вида- конкурента. Об этом можно догадаться хотя бы потому, что r уже не в первый раз возникает в ходе нашего курса как фундаментальная мера состояния популяции

Основное отличие между внутривидовой и межвидовой конкуренцией Можно ли вымереть в результате внутривидовой конкуренции? Нет (кроме каких-то экзотических случаев) Можно ли вымереть в результате межвидовой конкуренции? Да
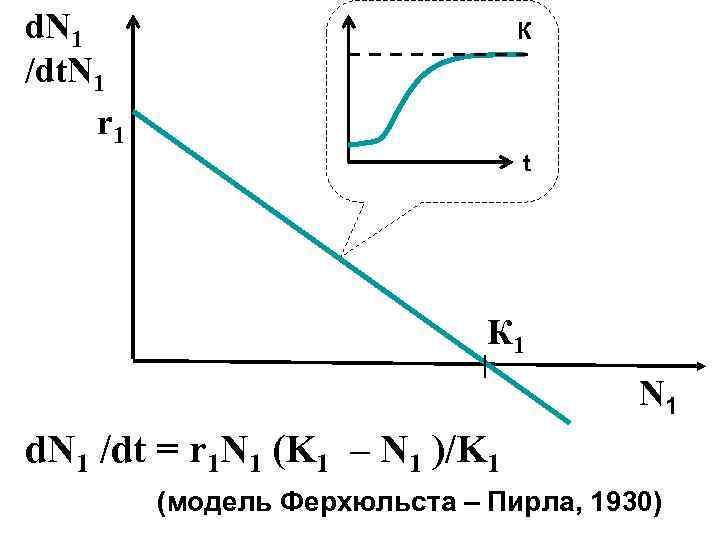
d. N 1 /dt. N 1 r 1 К t К 1 N 1 d. N 1 /dt = r 1 N 1 (K 1 – N 1 )/K 1 (модель Ферхюльста – Пирла, 1930)

Vito Volterra (1860 -1940)
Alfred James Lotka (1880 -1949)
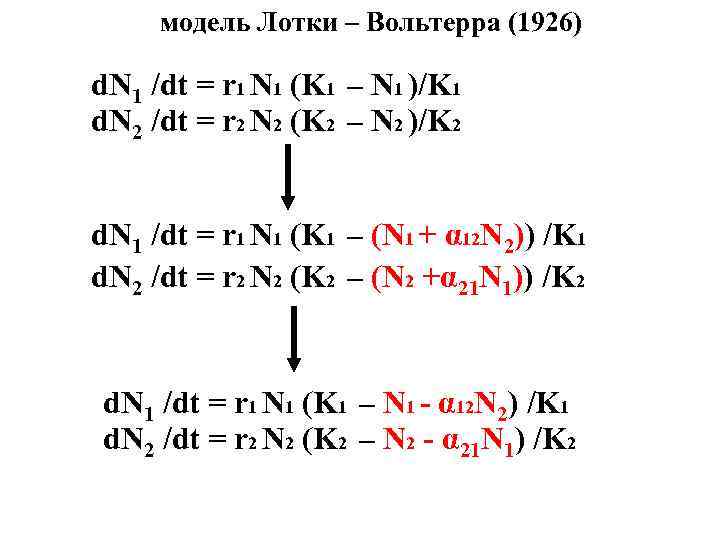
модель Лотки – Вольтерра (1926) d. N 1 /dt = r 1 N 1 (K 1 – N 1 )/K 1 d. N 2 /dt = r 2 N 2 (K 2 – N 2 )/K 2 d. N 1 /dt = r 1 N 1 (K 1 – (N 1 + α 12 N 2)) /K 1 d. N 2 /dt = r 2 N 2 (K 2 – (N 2 +α 21 N 1)) /K 2 d. N 1 /dt = r 1 N 1 (K 1 – N 1 - α 12 N 2) /K 1 d. N 2 /dt = r 2 N 2 (K 2 – N 2 - α 21 N 1) /K 2
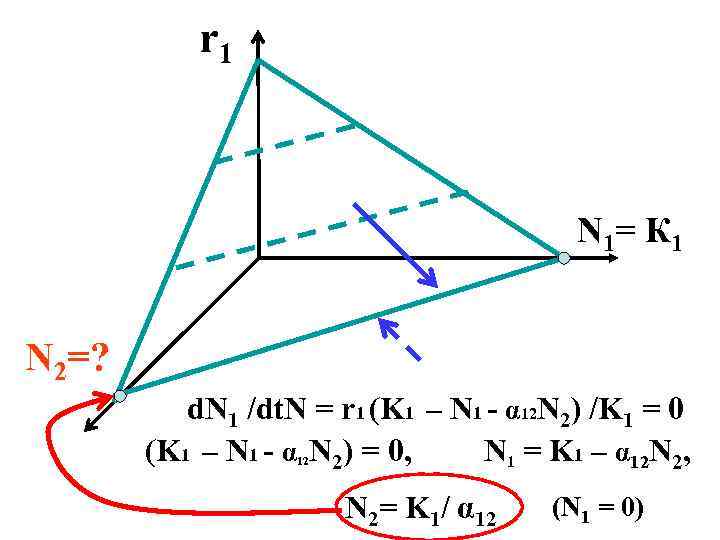
r 1 N 1= К 1 N 2=? d. N 1 /dt. N = r 1 (K 1 – N 1 - α 12 N 2) /K 1 = 0 (K 1 – N 1 - α N 2) = 0, N 1 = K 1 – α 12 N 2, 12 N 2= K 1/ α 12 (N 1 = 0)
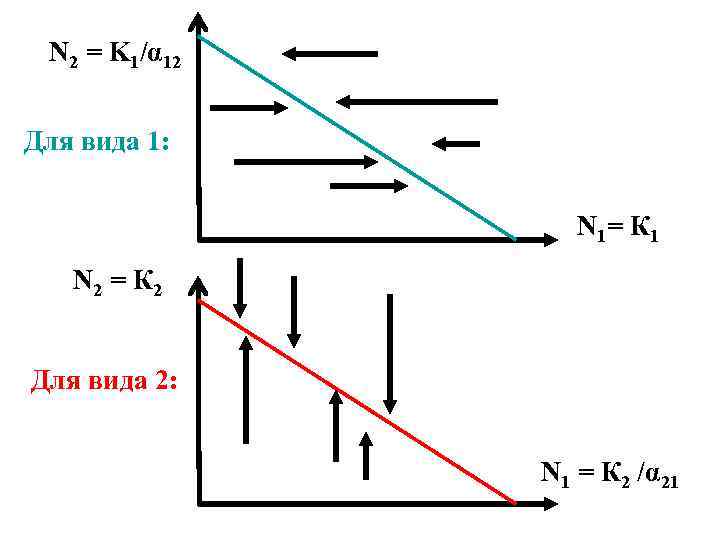
N 2 = K 1/α 12 Для вида 1: N 1= К 1 N 2 = К 2 Для вида 2: N 1 = К 2 /α 21
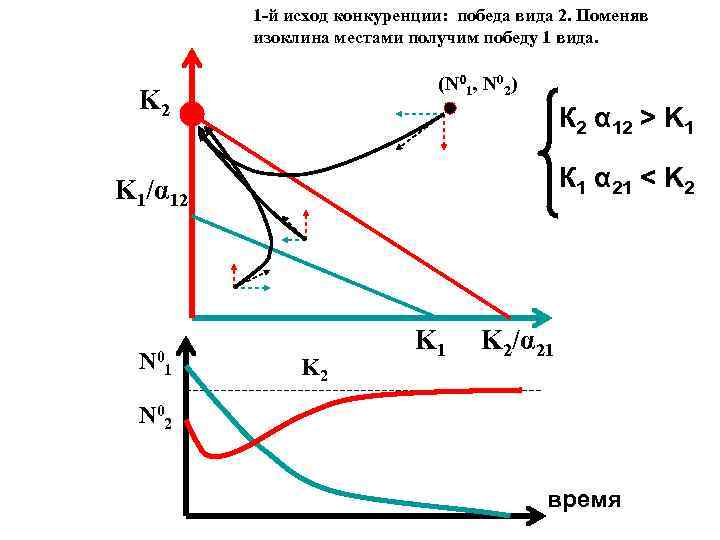
1 -й исход конкуренции: победа вида 2. Поменяв изоклина местами получим победу 1 вида. (N 01, N 02) K 2 К 2 α 12 > K 1 К 1 α 21 < K 2 K 1/α 12 N 0 1 K 2 K 1 K 2/α 21 N 02 время
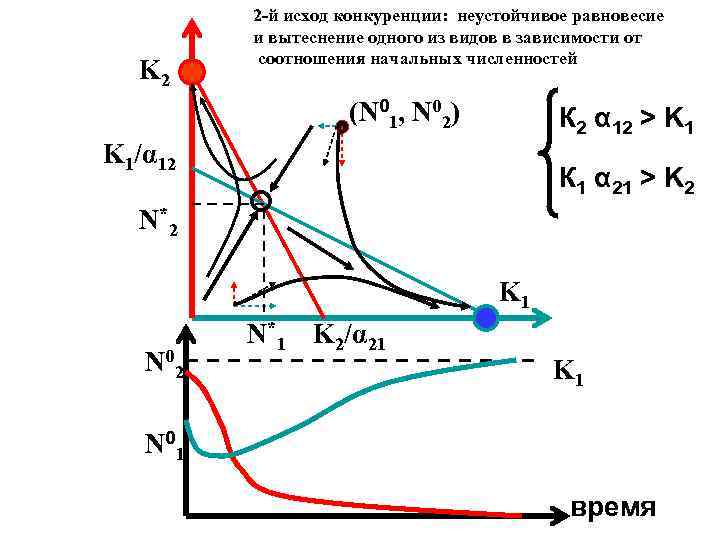
K 2 2 -й исход конкуренции: неустойчивое равновесие и вытеснение одного из видов в зависимости от соотношения начальных численностей (N 01, N 02) К 2 α 12 > K 1/α 12 К 1 α 21 > K 2 N*2 K 1 N 02 N*1 K 2/α 21 K 1 N 01 время
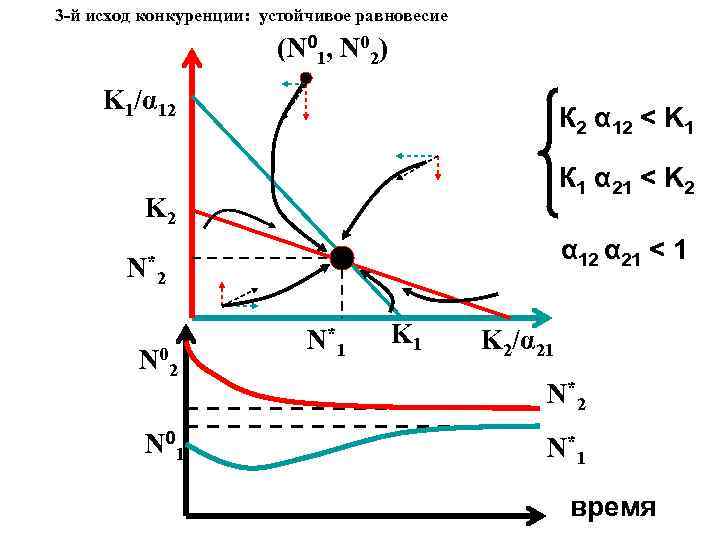
3 -й исход конкуренции: устойчивое равновесие (N 01, N 02) K 1/α 12 К 2 α 12 < K 1 К 1 α 21 < K 2 α 12 α 21 < 1 N*2 N 01 N*1 K 2/α 21 N*2 N*1 время

Проверка теории Георгий Францевич Гаузе (1910 -1986)

Г. Ф. ГАУЗЕ «Struggle for existence» Baltimore, 1934

Скорость прироста попул-ии в единицу времени = Потенциа льный прирост попул-ии в единицу времени = число особей x потенц-ое число их потомков X Степень прироста определяе тся числом незанятых мест в биотопе из Г. Ф. Гаузе (1934)
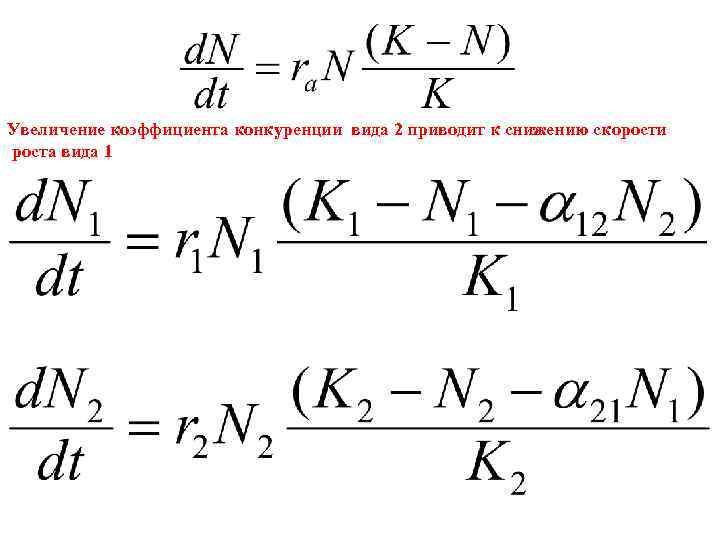
Увеличение коэффициента конкуренции вида 2 приводит к снижению скорости роста вида 1
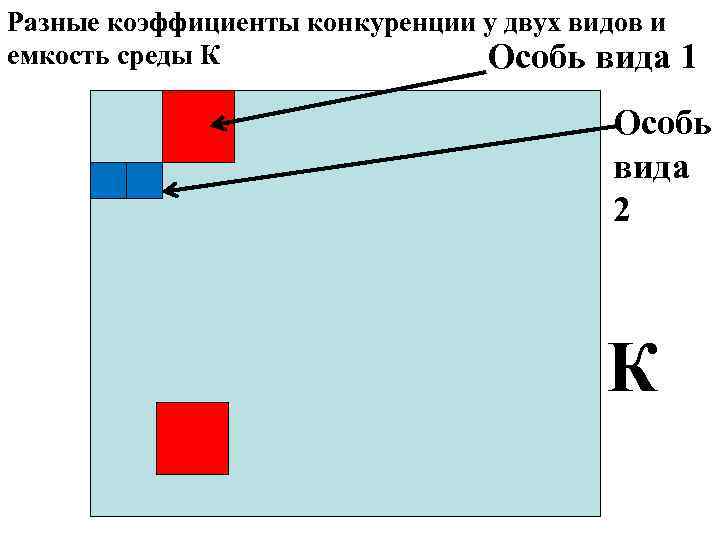
Разные коэффициенты конкуренции у двух видов и емкость среды К Особь вида 1 Особь вида 2 К
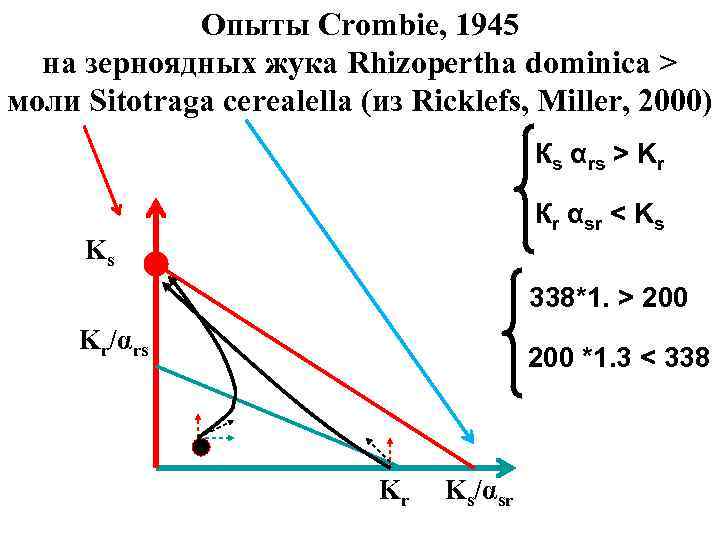
Опыты Crombie, 1945 на зерноядных жука Rhizopertha dominica > моли Sitotraga cerealella (из Ricklefs, Miller, 2000) Кs αrs > Kr Кr αsr < Ks Ks 338*1. > 200 Kr/αrs 200 *1. 3 < 338 Kr Ks/αsr
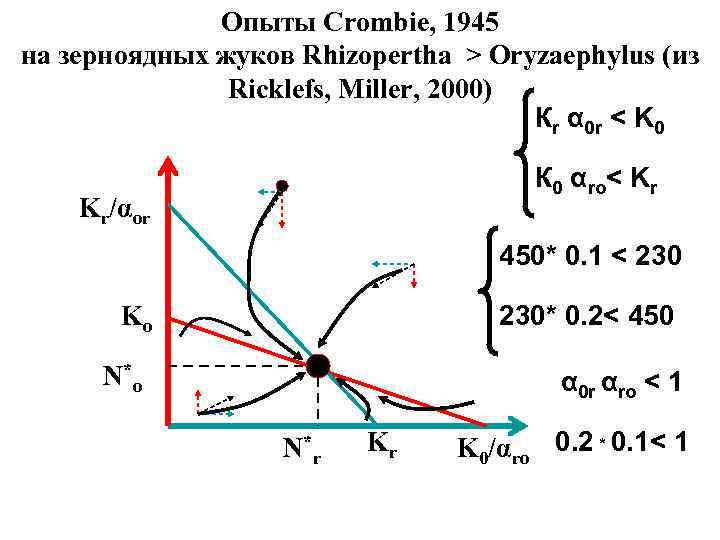
Опыты Crombie, 1945 на зерноядных жуков Rhizopertha > Oryzaephylus (из Ricklefs, Miller, 2000) Кr α 0 r < K 0 К 0 αro< Kr Kr/αor 450* 0. 1 < 230* 0. 2< 450 Ko N*o α 0 r αro < 1 N*r Kr K 0/αro 0. 2 * 0. 1< 1

Принцип Гаузе - Вольтерра (принцип конкурентного исключения) Два или более видов не могут совместно эксплуатировать ограниченный ресурс в гомогенной среде без того, чтобы один вид не вытеснил все остальные. Или: два и более вида не могут в общем пространстве занимать одну экологическую нишу

Экологическая ниша – «место» , занимаемое видом в сообществе • место можно понимать буквально – как место в пространстве, т. е. пространственное распределение вида (Grinnell) • место можно понимать как положение вида в цепях питания, т. е. как набор необходимых виду пищевых ресурсов (пищевых организмов, элементов минерального питания у растений и т. д. ) (Elton) • положение вида в многомерном пространстве условий и ресурсов (многомерная ниша Хатчинсона, Hutchinson)

Принцип конкурентного исключения ( «закон Гаузе» , «принцип Вольтерры – Гаузе» ) в современной трактовке: Число видов, неограниченно долго сосуществующих в постоянных условиях гомогенного местообитания с постоянными численностями, не может превышать числа плотностнозависимых факторов, лимитирующих развитие их популяций (вытекает также из ресурсной теории Дэвида Тильмана, см. ниже)

Как классическая модель конкуренции Вольтерры-Лотки соотносится с принципом конкурентного исключения Гаузе?

Ведь мы видели, что в одном случае из 4 -х устойчивое сосуществование возможно! В трех случаях из 4 -х, когда устойчивое сосуществование невозможно (побеждает один из конкурентов), один вид воздействует на другой или оба вида воздействуют друг на друга сильно. Это интерпретируется как ситуация, когда оба вида занимают одну и ту же экологическую нишу. В одном случае из 4 -х, когда устойчивое сосуществование возможно, виды воздействуют друг на друга слабо. Этот случай интерпретируется как ситуация, когда виды занимают разные экологические ниши.
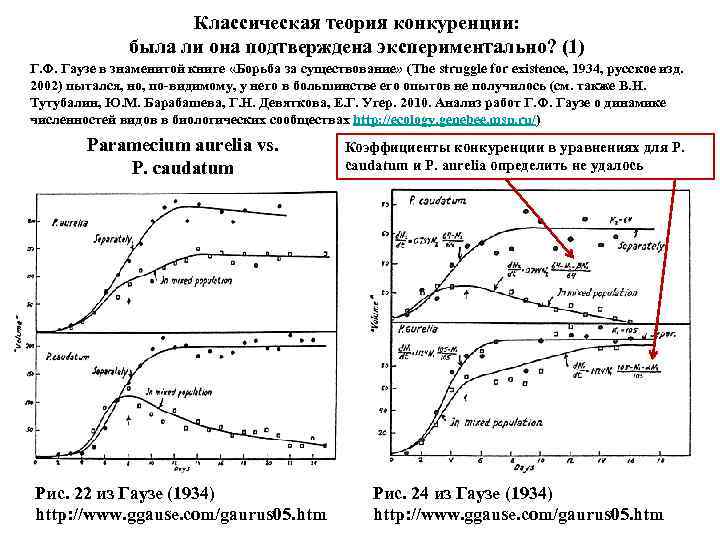
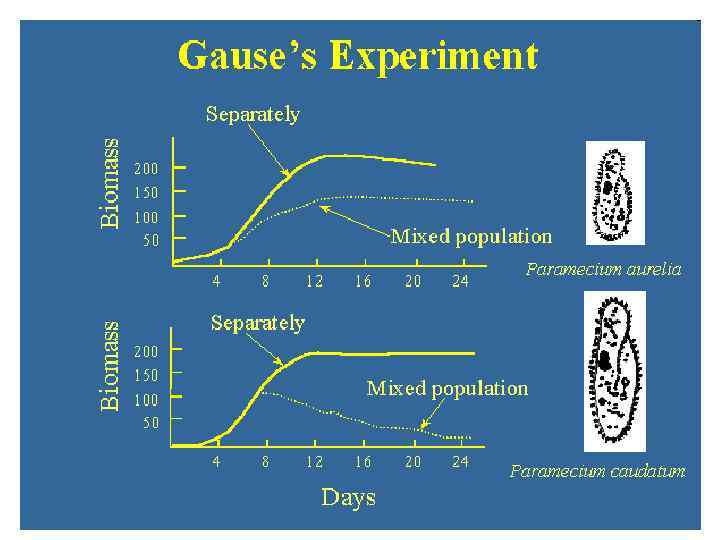
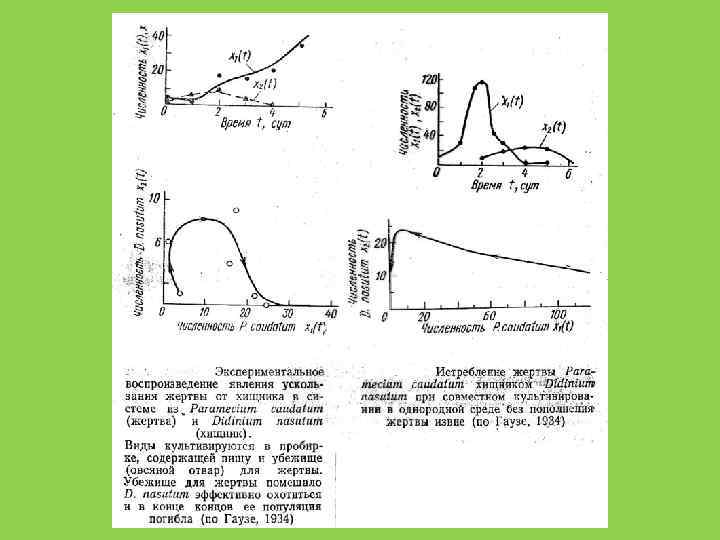
Классическая теория конкуренции: была ли она подтверждена экспериментально? (1) Г. Ф. Гаузе в знаменитой книге «Борьба за существование» (The struggle for existence, 1934, русское изд. 2002) пытался, но, по-видимому, у него в большинстве его опытов не получилось (см. также В. Н. Тутубалин, Ю. М. Барабашева, Г. Н. Девяткова, Е. Г. Угер. 2010. Анализ работ Г. Ф. Гаузе о динамике численностей видов в биологических сообществах http: //ecology. genebee. msu. ru/) Paramecium aurelia vs. P. caudatum Коэффициенты конкуренции в уравнениях для P. caudatum и P. aurelia определить не удалось Рис. 22 из Гаузе (1934) http: //www. ggause. com/gaurus 05. htm Рис. 24 из Гаузе (1934) http: //www. ggause. com/gaurus 05. htm

Замечание Г. Ф. Гаузе к опытам с парамециями: «Нам остается теперь рассмотреть второй этап конкуренции, т. е. непосредственное вытеснение одного вида другим. […] В наших опытах главным фактором, регулирующим скорость потока популяции, было следующее техническое мероприятие: ежедневно бралась проба, равная 1/10 части популяции, которая затем отбрасывалась. […] Ежедневно биомасса каждого вида уменьшалась на 1/10 часть. Если бы виды были одинаковы по своим свойствам, то каждый из них снова увеличился бы на 1/10, и не происходило бы никакого изменения соотношений между видами. Однако, так как один вид растет скорее другого, то он успевает не только восполнить свою потерю, но и захватить часть пищевых ресурсов другого вида. В результате, каждое элементарное движение популяции приводит к уменьшению биомассы медленно растущего вида и заканчивается в конце концов полным его исчезновением. » (Gause 1934, цитируется по Гаузе 2002, с. 108) (См. также М. Уильямсон. 1975. Анализ биологических популяций, с. 169) Но изъятие особей, то есть дополнительный источник смертности, не предусмотрен моделью Вольтерры-Лотки!
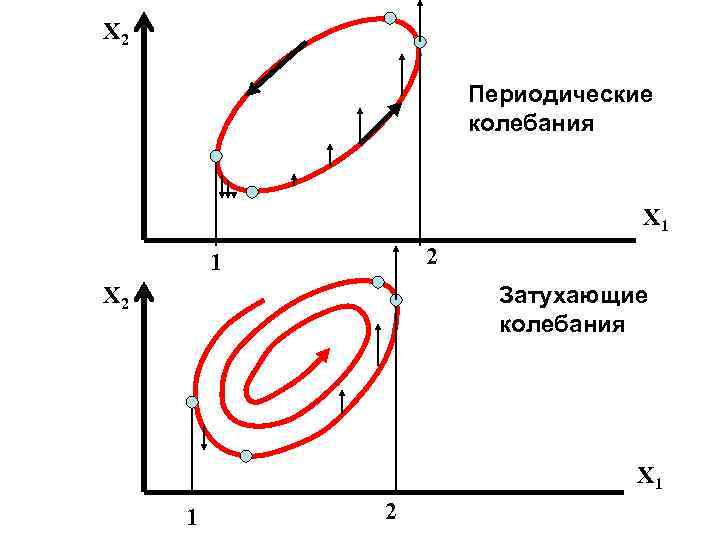
X 2 Периодические колебания X 1 2 1 X 2 Затухающие колебания X 1 1 2
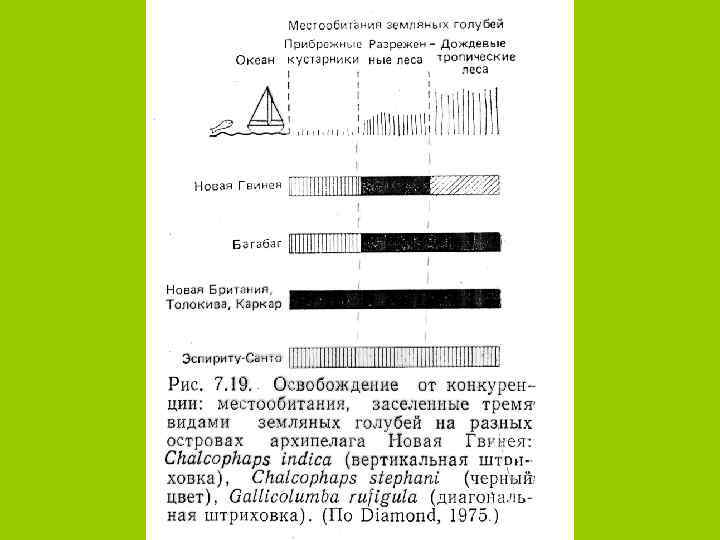

оля особей данного размерного класса, % 20 Остров Абингтон о-в Чарльз о-в Дафне о-в Кроссман Высота клюва, мм
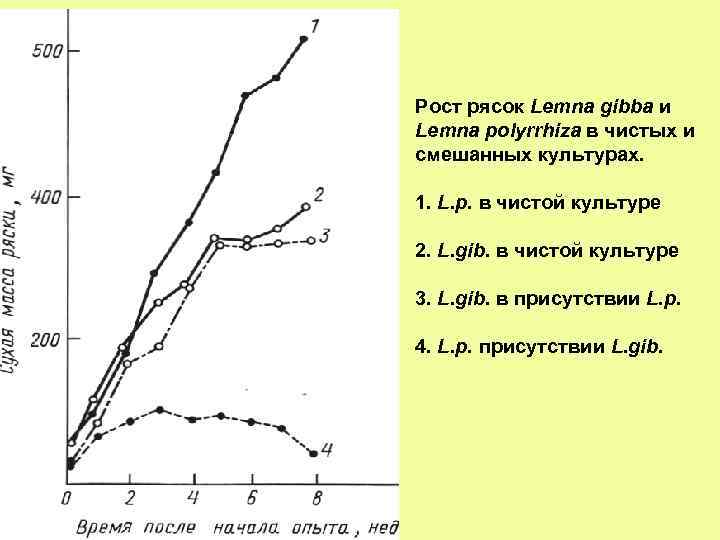
Рост рясок Lemna gibba и Lemna polyrrhiza в чистых и смешанных культурах. 1. L. p. в чистой культуре 2. L. gib. в чистой культуре 3. L. gib. в присутствии L. p. 4. L. p. присутствии L. gib.

Joseph Connell «The ghost of competition past»
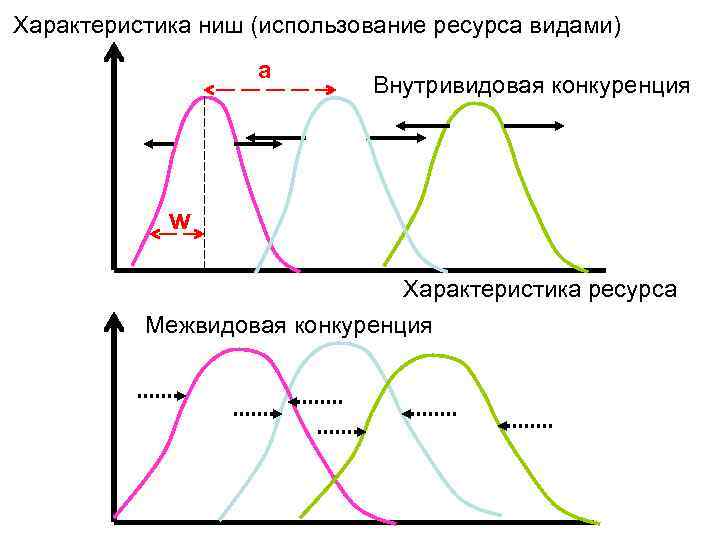
Характеристика ниш (использование ресурса видами) а Внутривидовая конкуренция w Характеристика ресурса Межвидовая конкуренция

Два способа достичь сосуществования: 1. Виды расходятся по разным экологическим нишам: соответственно, конкуренция между ними отсутствует или же резко ослаблена.

• Сосуществование «сильного» и «быстрого» , виолента и эксплерента, К- и r-стратегов (пример: 2 вида Bromus spp. ) • эфемерный биотоп

Система Раменского - Грайма J Philip Grime Леонтий Григорьевич Раменский
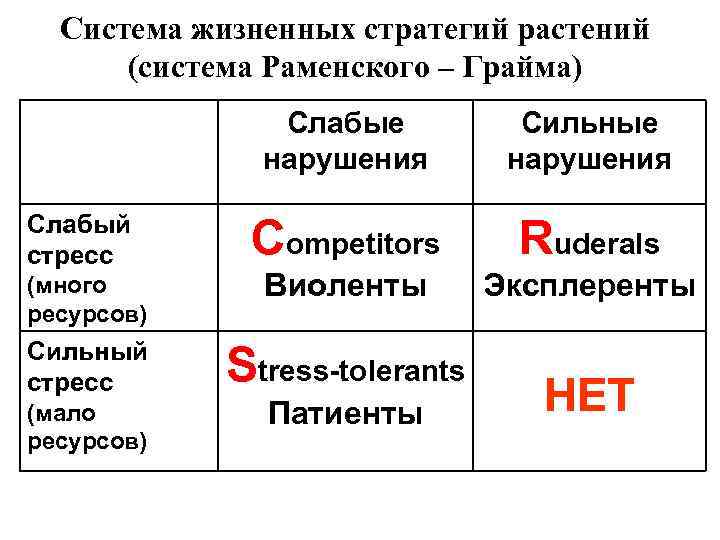
Система жизненных стратегий растений (система Раменского – Грайма) Слабые нарушения Сильные нарушения Competitors Ruderals (много ресурсов) Виоленты Эксплеренты Сильный стресс Stress-tolerants Слабый стресс (мало ресурсов) Патиенты НЕТ

Два способа достичь сосуществования: 2. Виды занимают одну экологическую нишу, конкурируют за общие ресурсы, но вытеснение одного вида другим откладывается на долгое время, прерывается извне или же не допускается путем интерференции (ингибирования одних видов другими).

Способы сосуществования видов, занимающих одну и ту же экологическую нишу: 1. Ограничение разными ресурсами. 2. Смена конкурентного преимущества по мере расходования лимитирующего ресурса или же, наоборот, дополнительного его поступления в среду. 3. Прерывание процесса вытеснения нарушениями извне за счет абиотических (пожары, осыпи и т. п. ) или биотических факторов (выедание, вытаптывание). 4. Интерференция – ингибирование одних видов другими за счет специально выделяемых веществ. 5. Конвергенция разных видов, направленная на возрастание экологического сходства (сосуществование за счет «отложенного вытесенения» ). 6. Мутуалистические взаимоотношения между видами, иногда опосредованные (например, через микоризу). 7. Гетерогенная среда (эфемерный биотоп)

1. Ограничение разными ресурсами* (или разными хищниками) *что можно рассматривать и как разные ниши

Ресурсная теория конкуренции Тильмана (David Tilman) (resource-based competition theory) (1) В теории в явном виде присутствуют ресурсы (или ресурс, если конкуренция за один ресурс) – в классической теории конкуренции Вольтерры-Лотки ресурсов нет! (2) Успех вида в конкуренции определяется пороговой концентрацией ресурса для этого вида, а возможность сосуществования с др. видами – скоростью потребления лимитирующего ресурса (наклоном вектора потребления в точке равновесия) (3) Это – графическая теория. Графическая теория не заменяет строгой математической теории. Однако теория, изложенная на графическом языке, часто (хотя не всегда!) обладает большей общностью и всегда обладает большей наглядностью, что облегчает ее восприятие и открывает возможность для экспериментальной проверки

Два типа экологических факторов: условия и ресурсы Условия (или условия существования): температура, соленость, влажность, то есть то, что является характеристикой среды, не зависящей или как правило не зависящей от жизнедеятельности организмов. Ресурсы: биогены (зот, фосфор), вода и свет для растений (хотя свет для растений является и условием), пища для животных, то есть то, что потребляется организмами ( «потребляется» в широком смысле, например, дупла для постройки гнезд или места для нереста не потребляются в буквальном смысле, но тоже являются ресурсами) и, таким образом, сильно зависит от количества организмов и от интенсивности их жизнедеятельности. «Точно так же, как нитраты, фосфаты и свет могут быть ресурсами для растения, нектар, пыльца и дупло в колоде могут быть ресурсами для пчелы, а желуди, орехи, прочие плоды и семена и дупло побольше – для белки. » (Tilman 1982, цит. по Бигон и др. Т. 1. 1989, с. 112) См. А. М. Гиляров. Популяционная экология. 1990, с. 7 М. Бигон, Дж. Харпер, К. Таунсенд. Экология: Особи, популяции и сообщества. Том 1. 1989, с. 64 -65, 112 -113
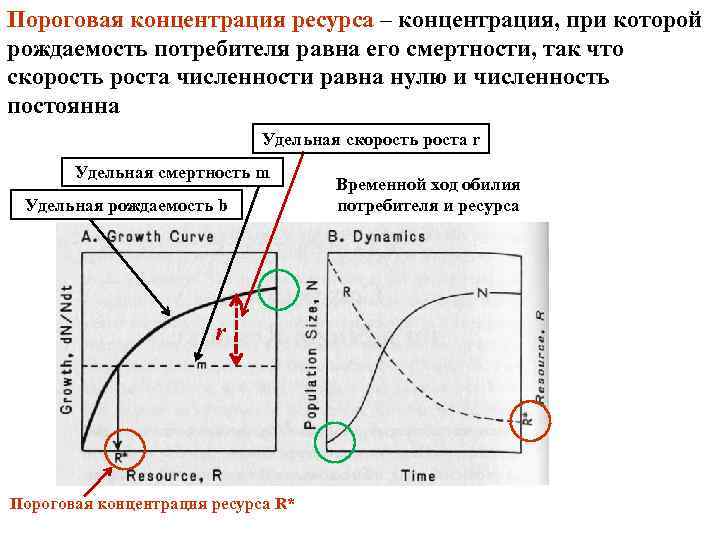
Пороговая концентрация ресурса – концентрация, при которой рождаемость потребителя равна его смертности, так что скорость роста численности равна нулю и численность постоянна Удельная скорость роста r Удельная смертность m Удельная рождаемость b r Пороговая концентрация ресурса R* Временной ход обилия потребителя и ресурса
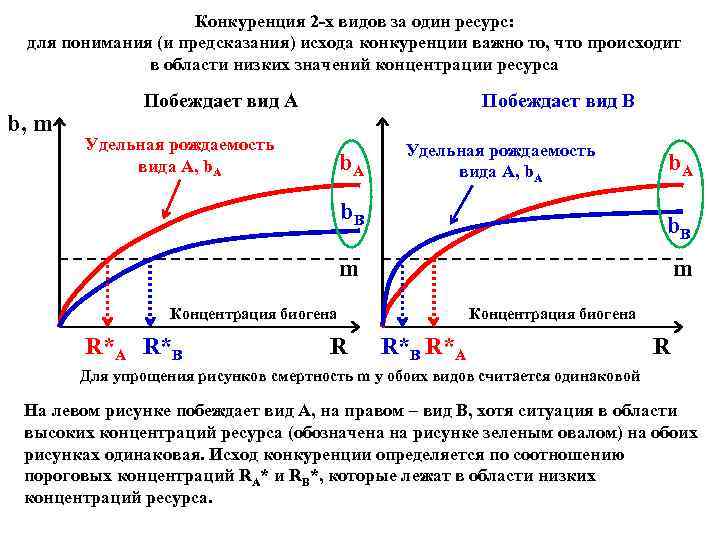
Конкуренция 2 -х видов за один ресурс: для понимания (и предсказания) исхода конкуренции важно то, что происходит в области низких значений концентрации ресурса b, m Побеждает вид A Побеждает вид B Удельная рождаемость вида A, b. A b. B m m Концентрация биогена R*A R*B R Концентрация биогена R*B R*A R Для упрощения рисунков смертность m у обоих видов считается одинаковой На левом рисунке побеждает вид A, на правом – вид B, хотя ситуация в области высоких концентраций ресурса (обозначена на рисунке зеленым овалом) на обоих рисунках одинаковая. Исход конкуренции определяется по соотношению пороговых концентраций RA* и RB*, которые лежат в области низких концентраций ресурса.

Конкуренция n (произвольного числа) видов за один ресурс: механизм конкурентного вытеснения В случае n видов, упорядоченных по пороговой концентрации ресурса R 1* < R 2* < R 3* < … < Rn*, теория предсказывает, что первый вид (т. е. вид с самой низкой пороговой концентрацией ресурса) вытесняет всех остальных, второй – всех, кроме первого, и т. д. Поскольку такое упорядочивание всегда можно осуществить (точное совпадение R* у разных видов маловероятно), отсюда следует принцип конкурентного исключения Гаузе. В отличие от расплывчатой стандартной формулировки этого принципа «виды не могут сосуществовать, если они занимают одинаковую экологическую нишу» , мы имеем новую формулировку: виды, потребляющие один и тот же ресурс (и в этом смысле занимающие одну и ту же пищевую нишу), не могут сосуществовать в силу того, что характерные для них пороговые концентрации ресурса различаются. Более того, мы не просто утверждаем, что виды не могут сосуществовать, но еще и предсказываем исход конкуренции на основании характерной для вида пороговой концентрации ресурса: побеждает тот вид, у которого пороговая концентрация ниже.

Величина пороговой концентрации ресурса R* легко укладывается в концепцию экологической ниши, поскольку представляет собой нижнюю границу диапазона толерантности по концентрации ресурса

Сравнение ресурсной теории конкуренции Тильмана и модели конкуренции Вольтерры-Лотки Ресурсная теория конкуренции Тильмана легко обобщается на произвольное число конкурирующих видов. В случае модели конкуренции Вольтерры-Лотки такое обобщение затруднительно или вовсе невозможно. Отчасти так происходит потому, что при учете ресурсов в явном виде прогноз исхода конкуренции сводится к рассмотрению только одной переменной – пороговой концентрации ресурса. Это существенно упрощает задачу прогноза по сравнению с той же задачей в рамках модели Вольтерры-Лотки – в ней исход конкуренции зависит от 4 -х переменных – 2 -х коэффициентов конкуренции и 2 -х значений емкости среды. Но дело не только в количественной стороне (сколько переменных), но и в качественной, т. к. пороговая концентрация – это переменная, имеющая реальный биологический смысл, поддающаяся оценке и действительно определяющая исход конкуренции.
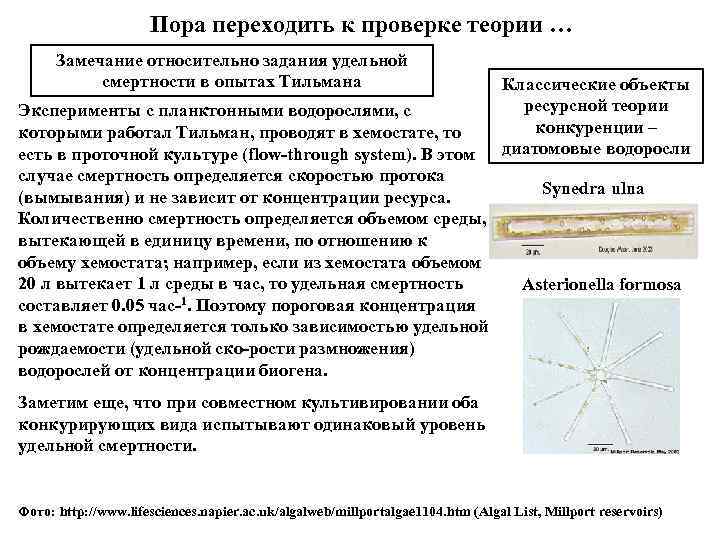
Пора переходить к проверке теории … Замечание относительно задания удельной смертности в опытах Тильмана Эксперименты с планктонными водорослями, с которыми работал Тильман, проводят в хемостате, то есть в проточной культуре (flow-through system). В этом случае смертность определяется скоростью протока (вымывания) и не зависит от концентрации ресурса. Количественно смертность определяется объемом среды, вытекающей в единицу времени, по отношению к объему хемостата; например, если из хемостата объемом 20 л вытекает 1 л среды в час, то удельная смертность составляет 0. 05 час-1. Поэтому пороговая концентрация в хемостате определяется только зависимостью удельной рождаемости (удельной ско-рости размножения) водорослей от концентрации биогена. Классические объекты ресурсной теории конкуренции – диатомовые водоросли Synedra ulna Asterionella formosa Заметим еще, что при совместном культивировании оба конкурирующих вида испытывают одинаковый уровень удельной смертности. Фото: http: //www. lifesciences. napier. ac. uk/algalweb/millportalgae 1104. htm (Algal List, Millport reservoirs)
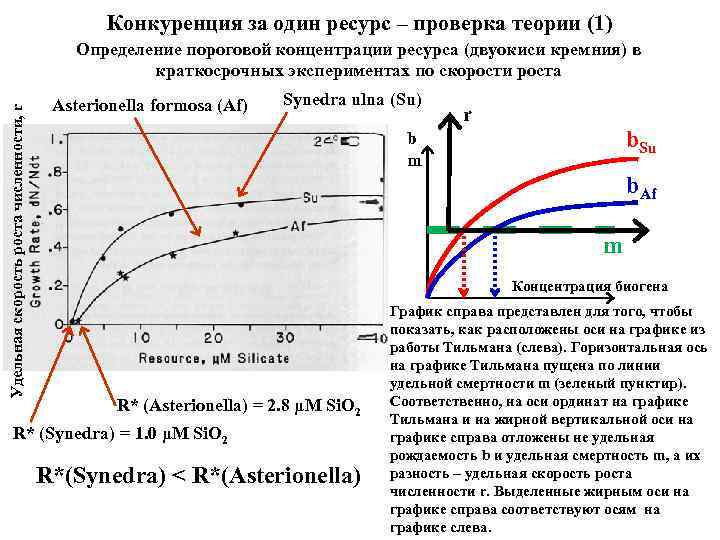
Конкуренция за один ресурс – проверка теории (1) Удельная скорость роста численности, r Определение пороговой концентрации ресурса (двуокиси кремния) в краткосрочных экспериментах по скорости роста Asterionella formosa (Af) Synedra ulna (Su) r b. Su b m b. Af m Концентрация биогена R* (Asterionella) = 2. 8 μM Si. O 2 R* (Synedra) = 1. 0 μM Si. O 2 R*(Synedra) < R*(Asterionella) График справа представлен для того, чтобы показать, как расположены оси на графике из работы Тильмана (слева). Горизонтальная ось на графике Тильмана пущена по линии удельной смертности m (зеленый пунктир). Соответственно, на оси ординат на графике Тильмана и на жирной вертикальной оси на графике справа отложены не удельная рождаемость b и удельная смертность m, а их разность – удельная скорость роста численности r. Выделенные жирным оси на графике справа соответствуют осям на графике слева.
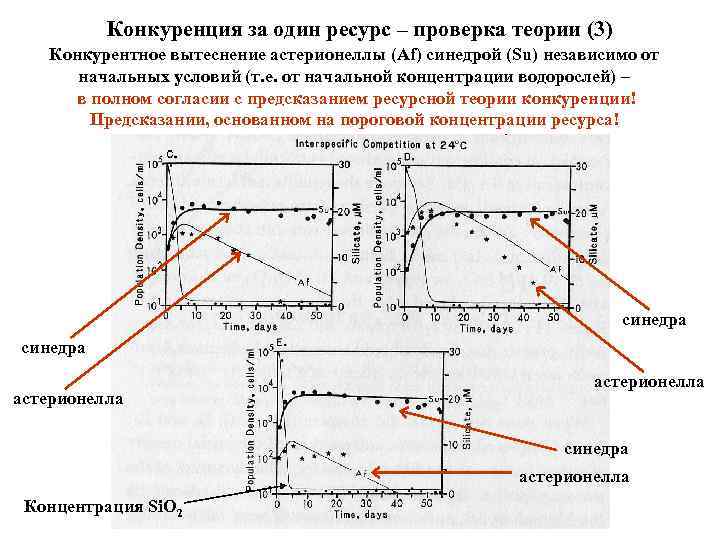
Конкуренция за один ресурс – проверка теории (3) Конкурентное вытеснение астерионеллы (Af) синедрой (Su) независимо от начальных условий (т. е. от начальной концентрации водорослей) – в полном согласии с предсказанием ресурсной теории конкуренции! Предсказании, основанном на пороговой концентрации ресурса! синедра астерионелла Концентрация Si. O 2
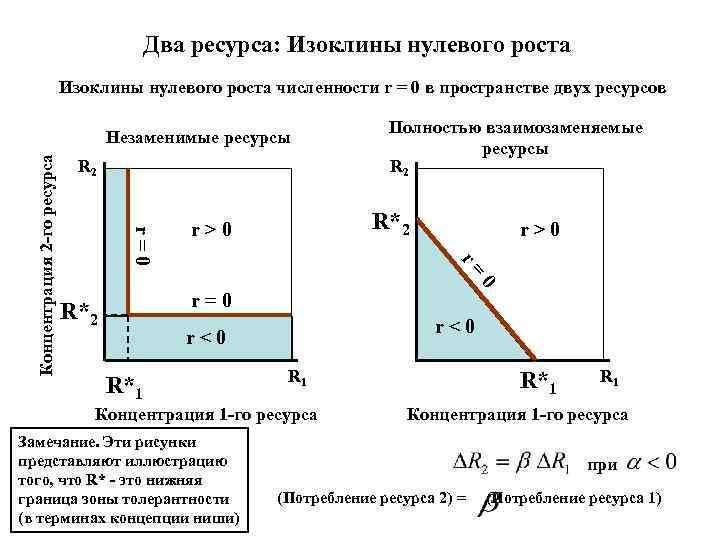
Два ресурса: Изоклины нулевого роста численности r = 0 в пространстве двух ресурсов R 2 Полностью взаимозаменяемые ресурсы R 2 R*2 r > 0 r = 0 0 Концентрация 2 -го ресурса Незаменимые ресурсы r = 0 R*2 r < 0 R*1 R 1 Концентрация 1 -го ресурса Замечание. Эти рисунки представляют иллюстрацию того, что R* - это нижняя граница зоны толерантности (в терминах концепции ниши) R*1 R 1 Концентрация 1 -го ресурса при (Потребление ресурса 2) = (Потребление ресурса 1)

Два ресурса: Вектора C и U Вектор потребления C, «вектор снабжения» U и ресурсная точка (S 1, S 2) Вектор потребления C – это вектор, проекции которого на оси ресурсов представляют собой скорости потребления соответствующих ресурсов при данной концентрации ресурсов (т. е. в данной точке пространства (R 1, R 2)). Таким образом, наклон вектора потребления (точнее, тангенс угла наклона) – это отношение скорости потребления ресурса 2 к скорости потребления ресурса 1 Вектор поступления ресурсов U и ресурсная точка (S 1, S 2) Вектор потребления C и вектор удельного R 2 потребления Вектор U всегда направлен в точку (S 1, S 2) R 2 или S 2 (S 1, S 2) α∙(S 2 - R 2’) N*c 1 C R 2 ’ U α∙(S 1 - R 1’) N*c 2 R 1 ’ R 1 или S 1

Ресурсная точка (S 1, S 2) и «вектор снабжения» U ( «вектор снабжения» = вектор поступления ресурсов) Ресурсная точка (S 1, S 2) в пространстве 2 -х ресурсов (R 1, R 2) обозначает максимальную концентрацию каждого из ресурсов в данном местообитании. Скорость поступления ресурсов считается (задается в эксперименте или предполагается в природе) пропорциональной разнице между максимальной и текущей концентрацией ресурса. То есть при концентрации ресурса R скорость его поступления равна S – R, где S – максимальная концентрация ресурса в данном местообитании. В какой-то мере это предположение аналогично допущению логистической модели, что удельная скорость роста численности пропорциональна разности между емкостью среды и текущим значением численности, K – N. Поэтому вектор поступления ресурсов задается формулой (где α – коэффициент пропорциональности) Почему вектор поступления ресурсов U направлен из точки (R 1, R 2) в ресурсную точку (S 1, S 2)? Потому что U = (S 1 -R 1, S 2 -R 2) представляет собой разность между вектором, направленным в ресурсную точку, S = (S 1, S 2), и вектором текущей концентрации ресурсов R = (R 1, R 2): U = S - R. Вспомните, как складываются вектора в физике, и Вы сразу поймете эту фразу! R 2 или S 2 (S 1, S 2) R = S – U R (R 1, R 2) S R 1 или S 1
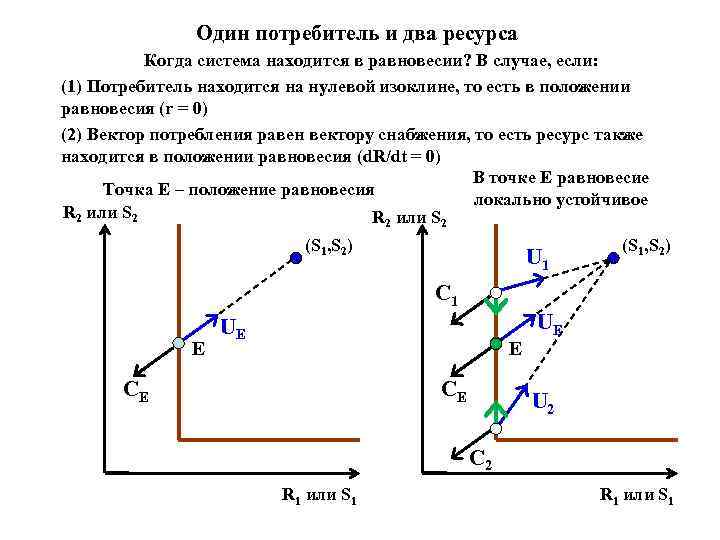
Один потребитель и два ресурса Когда система находится в равновесии? В случае, если: (1) Потребитель находится на нулевой изоклине, то есть в положении равновесия (r = 0) (2) Вектор потребления равен вектору снабжения, то есть ресурс также находится в положении равновесия (d. R/dt = 0) В точке E равновесие Точка E – положение равновесия локально устойчивое R 2 или S 2 (S 1, S 2) U 1 (S 1, S 2) C 1 E UE E CE CE UE U 2 C 2 R 1 или S 1

Как найти положение равновесия одного потребителя на двух ресурсах? • Построить нулевую изоклину потребителя • Построить вектор удельного потребления (можно в любой точке плоскости (R 1, R 2), но естественнее сделать это в какой-нибудь точке на нулевой изоклине – поскольку положение равновесие должно находиться на нулевой изоклине) • Нанести ресурсную точку • Провести через ресурсную точку линию, параллельную вектору потребления • Точка пересечения этой линии с нулевой изоклиной есть положение равновесия
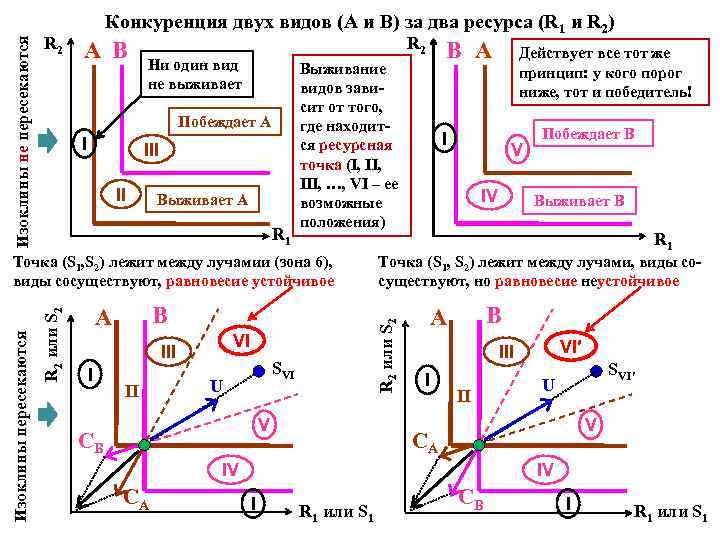
Изоклины не пересекаются R 2 Конкуренция двух видов (А и В) за два ресурса (R 1 и R 2) A B R 2 Ни один вид не выживает Побеждает A I II Выживает A R 1 Выживание видов зависит от того, где находится ресурсная точка (I, II, III, …, VI – ее возможные положения) B A VI III I II SVI U V CB I V IV Побеждает B Выживает B R 1 B A VI′ III I II SVI′ U V CA IV CA Действует все тот же принцип: у кого порог ниже, тот и победитель! Точка (S 1, S 2) лежит между лучами, виды сосуществуют, но равновесие неустойчивое R 2 или S 2 Изоклины пересекаются Точка (S 1, S 2) лежит между лучамии (зона 6), виды сосуществуют, равновесие устойчивое B A IV I R 1 или S 1 CB I R 1 или S 1
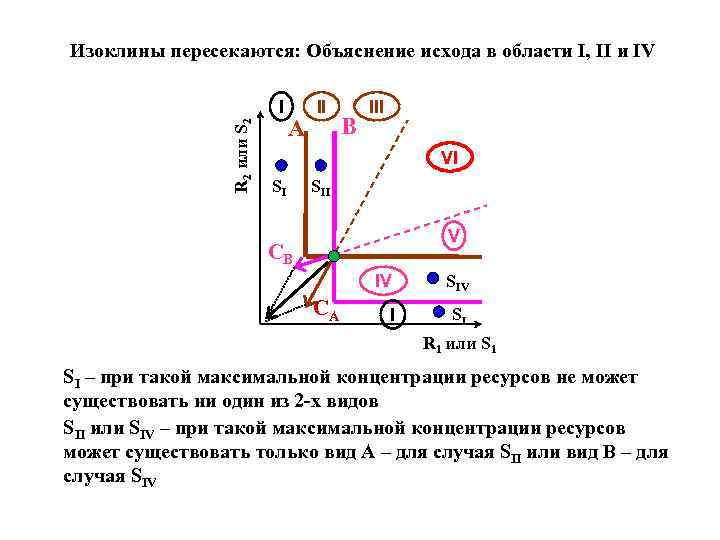
Изоклины пересекаются: Объяснение исхода в области I, II и IV R 2 или S 2 I A II B III VI SI SII V CB IV CA SIV I SI R 1 или S 1 SI – при такой максимальной концентрации ресурсов не может существовать ни один из 2 -х видов SII или SIV – при такой максимальной концентрации ресурсов может существовать только вид A – для случая SII или вид B – для случая SIV
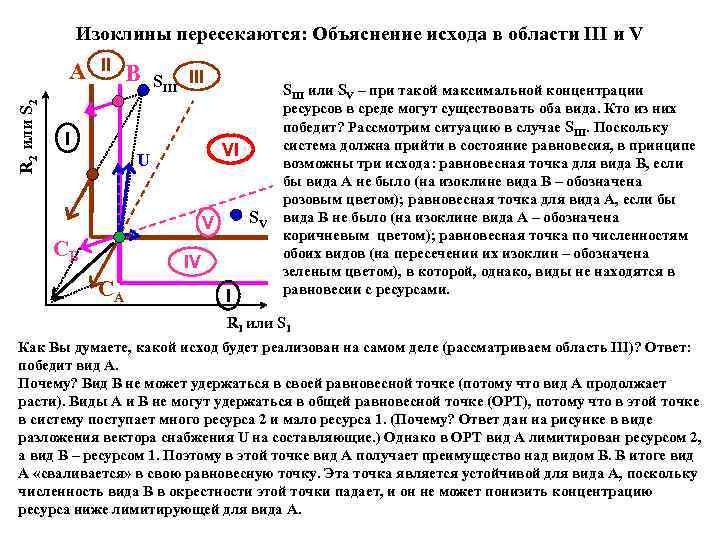
Изоклины пересекаются: Объяснение исхода в области III и V R 2 или S 2 A II B SIII I SIII или SV – при такой максимальной концентрации VI U SV V CB IV CA I ресурсов в среде могут существовать оба вида. Кто из них победит? Рассмотрим ситуацию в случае SIII. Поскольку система должна прийти в состояние равновесия, в принципе возможны три исхода: равновесная точка для вида B, если бы вида A не было (на изоклине вида В – обозначена розовым цветом); равновесная точка для вида А, если бы вида B не было (на изоклине вида А – обозначена коричневым цветом); равновесная точка по численностям обоих видов (на пересечении их изоклин – обозначена зеленым цветом), в которой, однако, виды не находятся в равновесии с ресурсами. R 1 или S 1 Как Вы думаете, какой исход будет реализован на самом деле (рассматриваем область III)? Ответ: победит вид А. Почему? Вид В не может удержаться в своей равновесной точке (потому что вид A продолжает расти). Виды A и В не могут удержаться в общей равновесной точке (ОРТ), потому что в этой точке в систему поступает много ресурса 2 и мало ресурса 1. (Почему? Ответ дан на рисунке в виде разложения вектора снабжения U на составляющие. ) Однако в ОРТ вид A лимитирован ресурсом 2, а вид B – ресурсом 1. Поэтому в этой точке вид A получает преимущество над видом B. В итоге вид А «сваливается» в свою равновесную точку. Эта точка является устойчивой для вида A, поскольку численность вида B в окрестности этой точки падает, и он не может понизить концентрацию ресурса ниже лимитирующей для вида A.
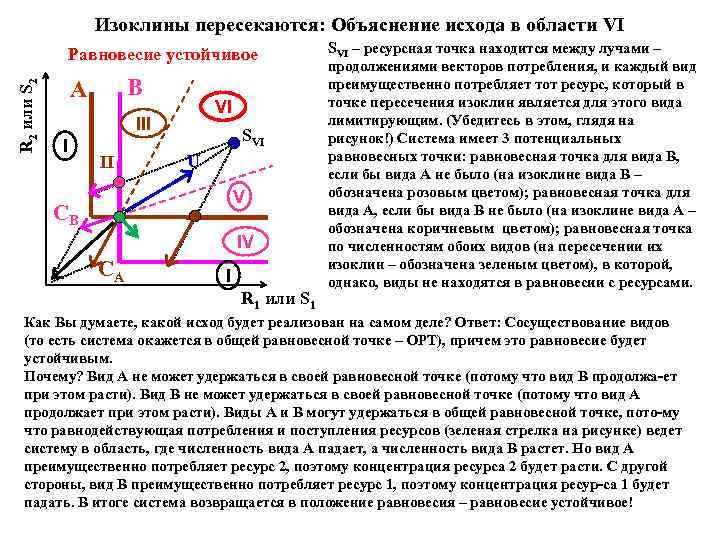
Изоклины пересекаются: Объяснение исхода в области VI R 2 или S 2 Равновесие устойчивое B A VI III I II SVI U V CB IV CA I R 1 или S 1 SVI – ресурсная точка находится между лучами – продолжениями векторов потребления, и каждый вид преимущественно потребляет тот ресурс, который в точке пересечения изоклин является для этого вида лимитирующим. (Убедитесь в этом, глядя на рисунок!) Система имеет 3 потенциальных равновесных точки: равновесная точка для вида B, если бы вида A не было (на изоклине вида В – обозначена розовым цветом); равновесная точка для вида А, если бы вида B не было (на изоклине вида А – обозначена коричневым цветом); равновесная точка по численностям обоих видов (на пересечении их изоклин – обозначена зеленым цветом), в которой, однако, виды не находятся в равновесии с ресурсами. Как Вы думаете, какой исход будет реализован на самом деле? Ответ: Сосуществование видов (то есть система окажется в общей равновесной точке – ОРТ), причем это равновесие будет устойчивым. Почему? Вид A не может удержаться в своей равновесной точке (потому что вид B продолжа-ет при этом расти). Вид B не может удержаться в своей равновесной точке (потому что вид A продолжает при этом расти). Виды A и В могут удержаться в общей равновесной точке, пото-му что равнодействующая потребления и поступления ресурсов (зеленая стрелка на рисунке) ведет систему в область, где численность вида A падает, а численность вида B растет. Но вид A преимущественно потребляет ресурс 2, поэтому концентрация ресурса 2 будет расти. С другой стороны, вид B преимущественно потребляет ресурс 1, поэтому концентрация ресур-са 1 будет падать. В итоге система возвращается в положение равновесия – равновесие устойчивое!
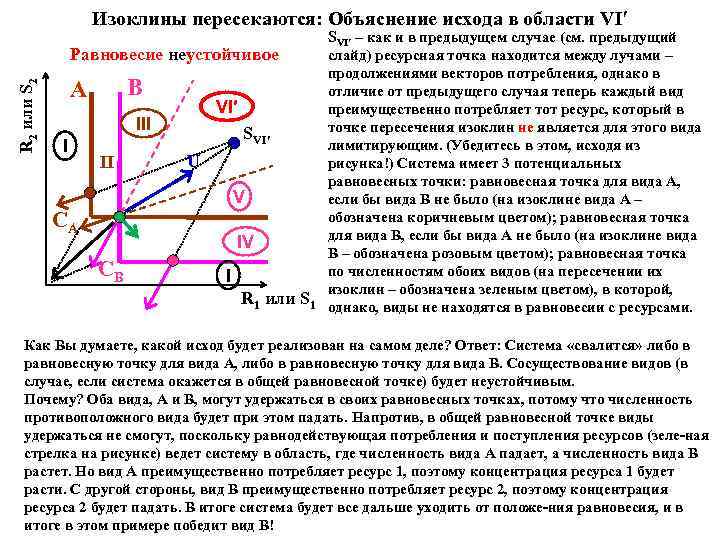
Изоклины пересекаются: Объяснение исхода в области VI′ R 2 или S 2 Равновесие неустойчивое B A VI′ III I II SVI′ U V CA IV CB I R 1 или S 1 SVI′ – как и в предыдущем случае (см. предыдущий слайд) ресурсная точка находится между лучами – продолжениями векторов потребления, однако в отличие от предыдущего случая теперь каждый вид преимущественно потребляет тот ресурс, который в точке пересечения изоклин не является для этого вида лимитирующим. (Убедитесь в этом, исходя из рисунка!) Система имеет 3 потенциальных равновесных точки: равновесная точка для вида A, если бы вида B не было (на изоклине вида A – обозначена коричневым цветом); равновесная точка для вида B, если бы вида A не было (на изоклине вида B – обозначена розовым цветом); равновесная точка по численностям обоих видов (на пересечении их изоклин – обозначена зеленым цветом), в которой, однако, виды не находятся в равновесии с ресурсами. Как Вы думаете, какой исход будет реализован на самом деле? Ответ: Система «свалится» либо в равновесную точку для вида A, либо в равновесную точку для вида B. Сосуществование видов (в случае, если система окажется в общей равновесной точке) будет неустойчивым. Почему? Оба вида, A и B, могут удержаться в своих равновесных точках, потому что численность противоположного вида будет при этом падать. Напротив, в общей равновесной точке виды удержаться не смогут, поскольку равнодействующая потребления и поступления ресурсов (зеле-ная стрелка на рисунке) ведет систему в область, где численность вида A падает, а численность вида B растет. Но вид A преимущественно потребляет ресурс 1, поэтому концентрация ресурса 1 будет расти. С другой стороны, вид B преимущественно потребляет ресурс 2, поэтому концентрация ресурса 2 будет падать. В итоге система будет все дальше уходить от положе-ния равновесия, и в итоге в этом примере победит вид B!

Конкуренция двух видов за два ресурса: заключение (1) Как определить, является ли равновесие устойчивым? При отклонении от положения равновесия надо задать следующие вопросы: Какой ресурс растет? Какой ресурс падает? Какой потребитель растет? Какой потребитель падает? Оказывается, что положение равновесия устойчиво, если при отклонении от положения равновесия (а) растет тот потребитель, который преимущественно потребляет тот ресурс, которого стало больше (б) падает тот потребитель, который преимущественно потребляет тот ресурс, которого стало меньше Если равновесие устойчивое, то при отклонении от него в рост должен пойти тот вид, который в большей мере потребляет тот ресурс, численность которого при отклонении от положения равновесия возросла, так что численность этого ресурса станет падать. Напротив, на спад должен пойти тот вид, который в большей мере потребляет тот ресурс, численность которого упала. Соответственно, потребление этого ресурса уменьшится, и его численность станет расти. В итоге система вернется в положение равновесия.

Конкуренция двух видов за два ресурса: заключение (2) Условия сосуществования (условия устойчивого равновесия): (1) Нулевые изоклины двух видов пересекаются. Точка пересечения нулевых изоклин – потенциальная точка равновесия (2) Ресурсная точка находится между лучами, являющимися продолжением векторов потребления (3) Вектора потребления наклонены таким образом, что для каждого вида выше скорость потребления того ресурса, который в точке пересечения изоклин является для этого вида лимитирующим. То есть получается, что вид в первую очередь лимитирует сам себя! Все эти условия должны выполняться одновременно
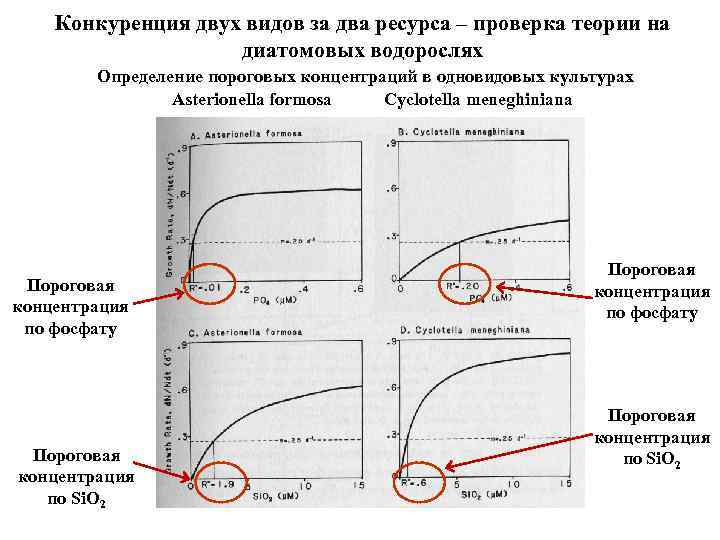
Конкуренция двух видов за два ресурса – проверка теории на диатомовых водорослях Определение пороговых концентраций в одновидовых культурах Asterionella formosa Cyclotella meneghiniana Пороговая концентрация по фосфату Пороговая концентрация по Si. O 2

Конкуренция двух видов за два ресурса – проверка теории на диатомовых водорослях График нулевых изоклин, построенный на основе пороговых концентраций по фосфату и силикату (ресурсы незаменимые) Asterionella formosa Cyclotella meneghiniana PO 4 r. A > 0 Si. O 2 r. C > 0 Si. O 2
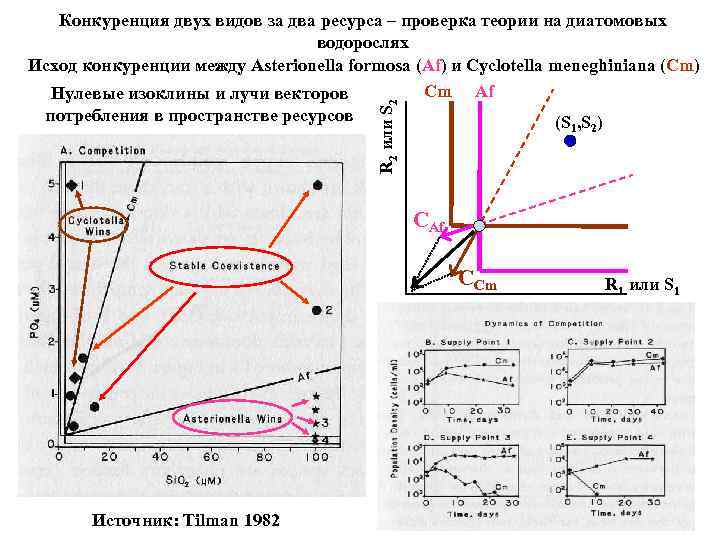
R 2 или S 2 Конкуренция двух видов за два ресурса – проверка теории на диатомовых водорослях Исход конкуренции между Asterionella formosa (Af) и Cyclotella meneghiniana (Cm) Cm Af Нулевые изоклины и лучи векторов потребления в пространстве ресурсов (S , S ) 1 2 CAf CCm Источник: Tilman 1982 R 1 или S 1

Сосуществование многих видов на ограниченном числе ресурсов и парадокс обогащения: проблемы в рамках классической теории конкуренции Проблема: несмотря на принцип конкурентного исключения, потребителей много Решения: 1) Диверсификация ниш Критика: (а) концепция ниши слишком расплывчата (даже между двумя особями легко найти различие в их предпочтениях, тем более это можно сделать между видами), (б) число существенных ресурсов, по кр. мере для растений, невелико (свет, вода, углекислый газ, N, P, K, Mg, Ca, ~15 микроэлементов) Проблема: с увеличением концентрации ресурса число сосуществующих видов-потребителей уменьшается

G. Evelyn Hutchinson Homage to Santa Rosalia, or why are there so many kinds of animals? // American Naturalist, 1959. V. 93: 145 -159

Примеры сосуществования многих видов на ограниченном числе ресурсов Планктонный парадокс Хатчинсона В верхнем освещенном и перемешиваемом слое водной толщи обитает множество организмов фитопланктона, ограниченных в своем развитии одними и теми же немногими ресурсами. Данная ситуация противоречит принципу конкурентного исключения Гаузе О планктонном парадоксе см. А. М. Гиляров. Популяционная экология. 1990, с. 163, 170 Из лекций А. М. Гилярова
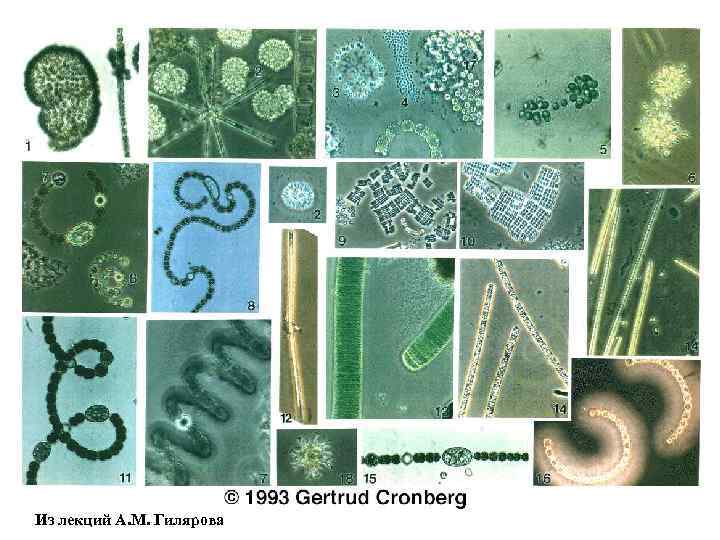
Из лекций А. М. Гилярова

Сосуществование многих видов и парадокс обогащения: Объяснение, предложенное Тильманом Основано на ресурсной теории конкуренции и пространственной неоднородности ресурсов (S 1, S 2) – «ресурсная точка» данного местообитания или микроместообитания Круги – контуры местообитаний с данной пространственной неоднородностью ресурсов Концентрация ресурса 2, R 2 S – максимальная концентрация ресурса в данном местообитании, «емкость среды» Следствия: 1) В бедной среде всего на двух ресурсах может сосуществовать много видов 2) С обогащением среды число видов уменьшается Концентрация ресурса 1, R 1 3) Видовой состав зависит от того, в каком направлении идет обогащение среды Семь видов (a, b, c, d, e, f, g) конкурируют за два ресурса (1 и 2). Линии, образующие прямой угол, представляют нулевые изоклины для каждого из семи видов в пространстве ресурсов. Наклонные линии представляют продолжения векторов потребления в точке равновесия пары видов. Сектора (a+b и т. д. ) есть множество точек (совокупность местообитаний), в которых «емкость среды» такова, что в них возможно сосуществование соответствующей пары видов (таких секторов шесть). Из Tilman 1982.

2. Смена конкурентного преимущества по мере расходования лимитирующего ресурса или дополнительного поступления его в среду (Сосуществование за счет «отложенного вытеснения» )
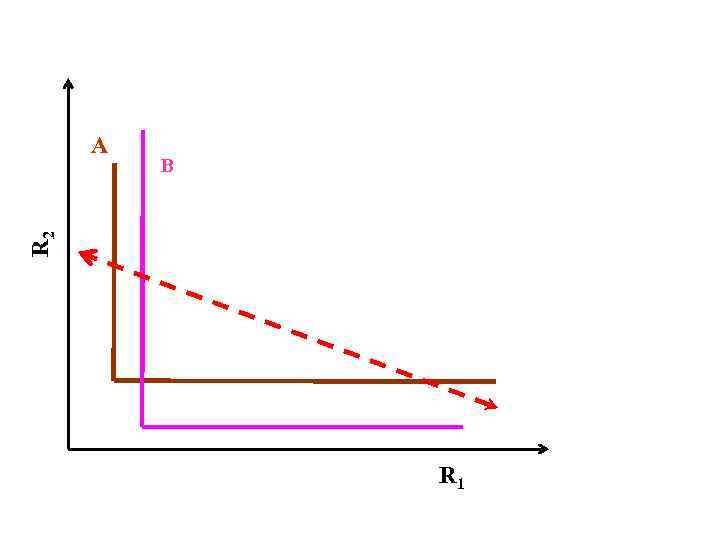
B R 2 A R 1

3. Прерывание процесса вытеснения нарушениями извне за счет абиотических (пожары, осыпи) или биотических факторов (выедание) (Сосуществование за счет «отложенного вытеснения» ; бурая водоросль и мидии; деревья в тайге)

4. Интерференция – ингибирование одних видов другими за счет специально выделяемых веществ

Три клона бактерий: 1) обычный (sensitive) 2) убийца (killer) 3) устойчивый (resistant) завоевывают поверхность питательной среды (один ресурс)

Скорость популяционного роста ( r ) данных штаммов: 1) Sensitive - r 2) Resistant – ½ r 3) Killer – ¼ r

Rock - scissors - paper Камень-ножницы-бумага
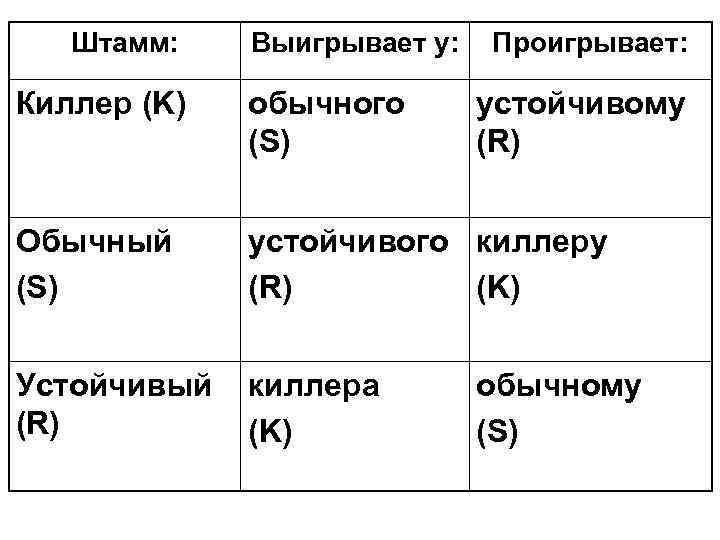
Штамм: Выигрывает у: Проигрывает: Киллер (K) обычного (S) устойчивому (R) Обычный (S) устойчивого киллеру (R) (K) Устойчивый (R) киллера (K) обычному (S)

5. Конвергенция разных видов, направленная на возрастание экологического сходства

Сосуществующие виды могут быть ЭКОЛОГИЧЕСКИ БЛИЗКИМИ. Это сходство может быть результатом отбора, протекавшего в сходных условиях и приведшего к конвергенции, а не дивергенции ниш

Часть страницы из журнала Nature V. 417. P. 480 -481 (30 May 2002). На фото: слева - Graham Bell, справа - Stephen Hubbell

Начало редакционной статьи Nature от 30 мая 2002 г.

Гипотеза нейтральности Стивена Хаббела

Гипотеза нейтральности Стивена Хаббела Виды сосуществуют потому, что в расчете на одну особь имеют примерно равные вероятности рождения, гибели и миграции Экологическая идентичность (или точнее - экологическая эквивалентность) видов, проявляется в сходстве их демографических характеристик

Хаббел и его сторонники вовсе не отрицают того, что разные виды в сообществе могут занимать разные ниш Они только замечают, что есть и другой способ достичь сосуществования, — быть максимально похожими по демографическим характеристикам, имет сходные удельные (в расчете на одну особь) скорости популяционного роста и заселения освободившихся участков

Нейтральная модель не отрицает существования разных экологических ниш. Но она утверждает, что предположение о расхождении ВСЕХ видов по разным нишам не является обязательным, чтобы объяснить их сосуществование. Предположение о НЕЙТРАЛЬНОСТИ должно приниматься как нуль-гипотеза при анализе всех многовидовых сообществ.
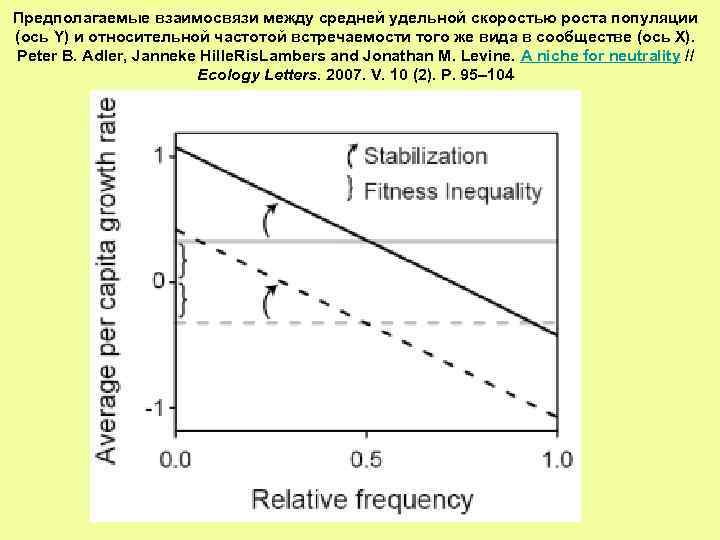
Предполагаемые взаимосвязи между средней удельной скоростью роста популяции (ось Y) и относительной частотой встречаемости того же вида в сообществе (ось Х). Peter B. Adler, Janneke Hille. Ris. Lambers and Jonathan M. Levine. A niche for neutrality // Ecology Letters. 2007. V. 10 (2). P. 95– 104
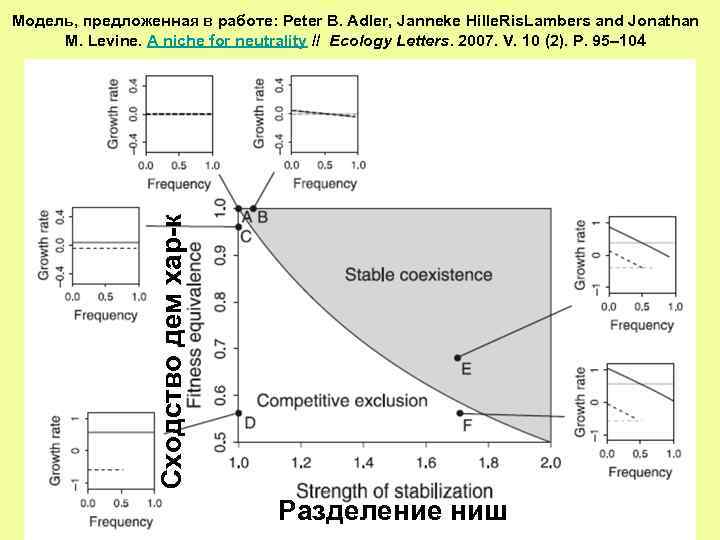
Сходство дем хар-к Модель, предложенная в работе: Peter B. Adler, Janneke Hille. Ris. Lambers and Jonathan M. Levine. A niche for neutrality // Ecology Letters. 2007. V. 10 (2). P. 95– 104 Разделение ниш

Рисунок показывает, как комбинация сходства демографических характеристик видов (ось Y) и степени разделения ниш (ось Х) может обеспечивать сосуществование видов. Разделение ниш характеризуется «степенью стабилизации» . Чем более схожи виды по скорости популяционного роста (значения по оси Y ближе к 1), тем меньше потребность в стабилизирующем механизме для достижения сосуществования. Если же виды по скорости популяционного роста сильно различаются (значения по оси Y ближе к 0), то их сосуществование возможно только за счет различия ниш (большей стабилизации). Область сосуществования — правая верхняя часть поля графика, а область конкурентного исключения — нижняя левая. Ситуации, складывающиеся при разном сочетании величин, отложенных по осям, отражены на графиках, вынесенных на поля. Механизму нейтральности соответствуют точки, лежащие в левой верхней части графика, а механизму разделения ниш — в правой нижней.

6. Мутуалистические взаимоотношения между видами, иногда опосредованные (например, через микоризу)

Net transfer of carbon between ectomycorrhizal tree species in the field SUZANNE W. SIMARD et al. , // Nature V. 388, pp. 579 - 582 (07 August 1997)

Сьюзан Симард и ее коллеги экспериментировали с саженцами березы бумажной (Betula papyrifera) и псевдотсуги Мензиса (Pseudotsuga menziesii), которые высаживались смешанными группами, так, что расстояния между растениями составляли около 0, 5 м. Опыты проводили в течение двух сезонов с деревьями, соответственно, 2=х и 3=х летнего возраста. Для того, чтобы выяснить, возможен ли обмен веществом между этими растениями, им давали порцию диоксида углерода СО 2, меченного для одного вида изотопом 13 С, а для другого - 14 С. Данную процедуру проводили, заключая отдельные растения в пластиковые мешки и подавая в них СО 2, содержащий тот или иной изотоп. Через 1, 5 недели после "подкормки" растений СО 2 их изымали и оценивали содержание каждого из использованных изотопов в тканях каждого растения отдельно. В ходе эксперимента было обнаружено, что между березой и псевдотсугой происходил взаимный обмен продуктами фотосинтеза, причем если в первый год он был примерно одинаков в обоих направлениях, то во второй год псевдотсуга была в явном выигрыше, получая от 2, 5 до 10% углерода, фиксированного обоими растениями. В некоторых вариантах опыта псевдотсугу до подкормки СО 2 в течение 4 -6 недель выдерживали в затенении, и именно в этом случае особенно возрастало потребление ею углерода, фиксированного березой. Результаты данного исследования невольно порождают ряд вопросов. Прежде всего, можно ли рассматривать обмен продуктами фотосинтеза как свидетельство взаимопомощи между деревьями разных видов? Если да, то как можно объяснить его возникновение в процессе эволюции, не вступая в противоречие с современным дарвинизмом и концепцией "эгоистичного гена"? Один из вариантов объяснения предполагает, что такой обмен есть всего-навсего побочный продукт коэволюции высших растений и грибов, а некоторая часть продукции, отдаваемая одним растением другому (который, возможно, является конкурентом), - это своего рода незначительная плата за громадные преимущества, предоставляемые микоризой. Не следует сбрасывать со счета и то, что донор может превратиться в рецепиента, если условия его существования ухудшаться.

Растения няни Alfonso Valiente-Banuet, Miguel Verdú Facilitation can increase the phylogenetic diversity of plant communities // Ecology Letters. 2007. V. 10 (11). P. 1029– 1036 Синопсис статьи смотрите здесь: «Растения-няни помогают поддерживать высокое разнообразие растительных сообществ» (http: //elementy. ru/news/430616)

Скопление растенийнянь и их подопечных в пустыне в Аризоне (район Tucson Mountains). Железное дерево Olneya tesota своей кроной дало приют «зеленому дереву» , Cercidium microphyllum (на переднем плане), а оно в свою очередь является няней для проростков кактуса сагуаро (Carnegia gigantea). Впрочем, скоро кактусы перерастут своих нянь

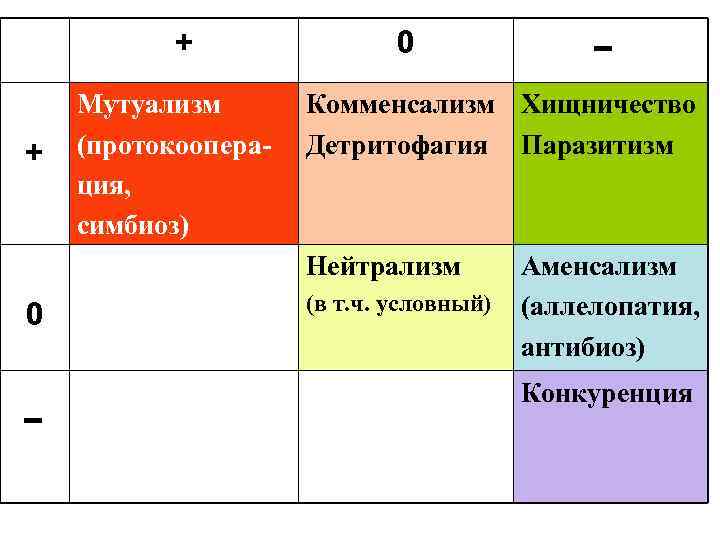
+ + Мутуализм (протокооперация, симбиоз) 0 Комменсализм Хищничество Детритофагия Паразитизм Нейтрализм 0 (в т. ч. условный) Аменсализм (аллелопатия, антибиоз) Конкуренция

Хищничество (эксплуатация, фитофагия, паразитизм) Predation, parasitism, plant herbivores
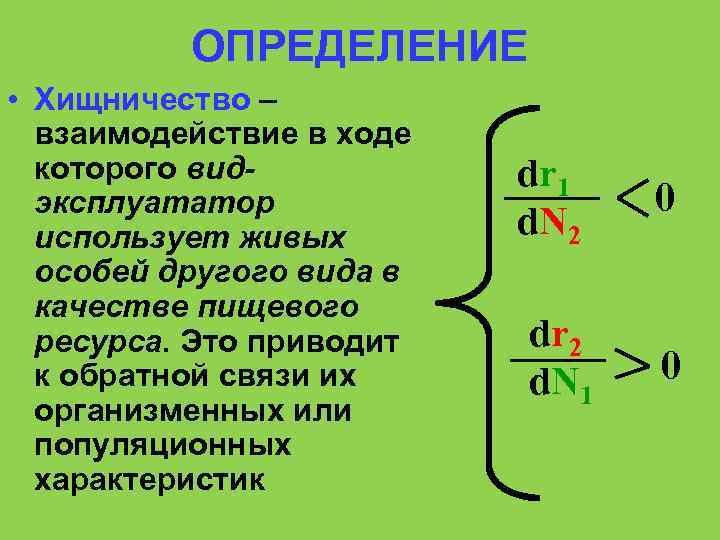
ОПРЕДЕЛЕНИЕ • Хищничество – взаимодействие в ходе которого видэксплуататор использует живых особей другого вида в качестве пищевого ресурса. Это приводит к обратной связи их организменных или популяционных характеристик dr 1 d. N 2 0 dr 2 d. N 1 0

• Отношения «эксплуататор жертва» в широком смысле, (включая отчасти комменсализм) и детритофагия (включая редуцентов) – основные пути передачи вещества и энергии в экосистемах

экосистемное определение • В экосистемах хищники выполняют функции консументов всех порядков
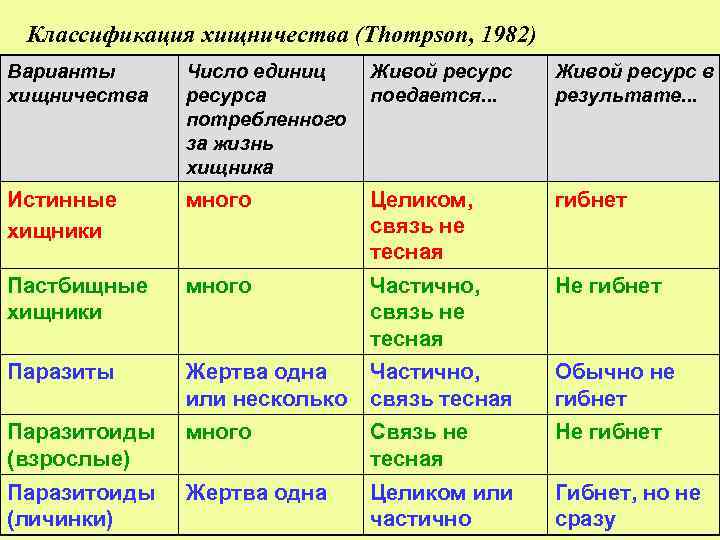
Классификация хищничества (Thompson, 1982) Варианты хищничества Число единиц ресурса потребленного за жизнь хищника Живой ресурс поедается. . . Живой ресурс в результате. . . Истинные хищники много Целиком, связь не тесная гибнет Пастбищные хищники много Частично, связь не тесная Не гибнет Паразиты Жертва одна или несколько Частично, связь тесная Обычно не гибнет Паразитоиды (взрослые) много Связь не тесная Не гибнет Паразитоиды (личинки) Жертва одна Целиком или частично Гибнет, но не сразу
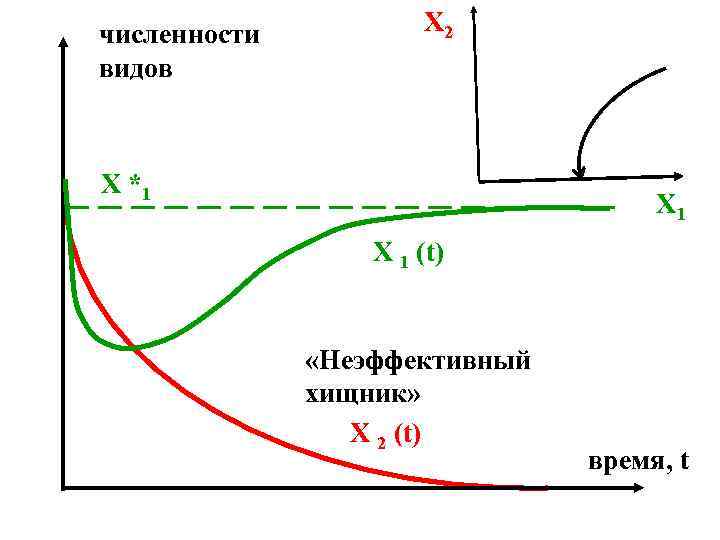
численности видов Х 2 X *1 Х 1 X 1 (t) «Неэффективный хищник» X 2 (t) время, t
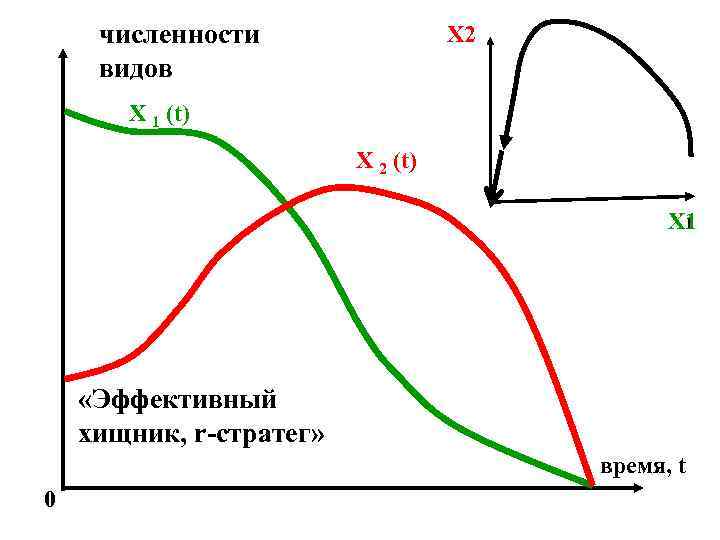
численности видов Х 2 X 1 (t) X 2 (t) Х 1 «Эффективный хищник, r-стратег» время, t 0
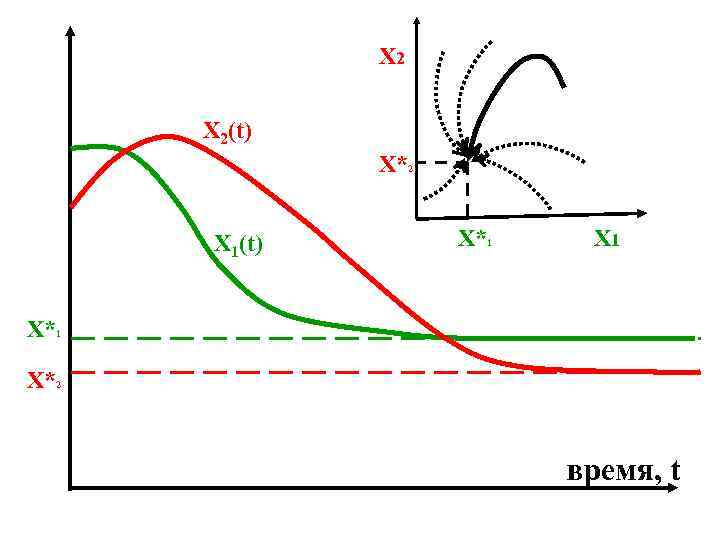
Х 2 X 2(t) X*2 X 1(t) X*1 Х 1 X*2 время, t
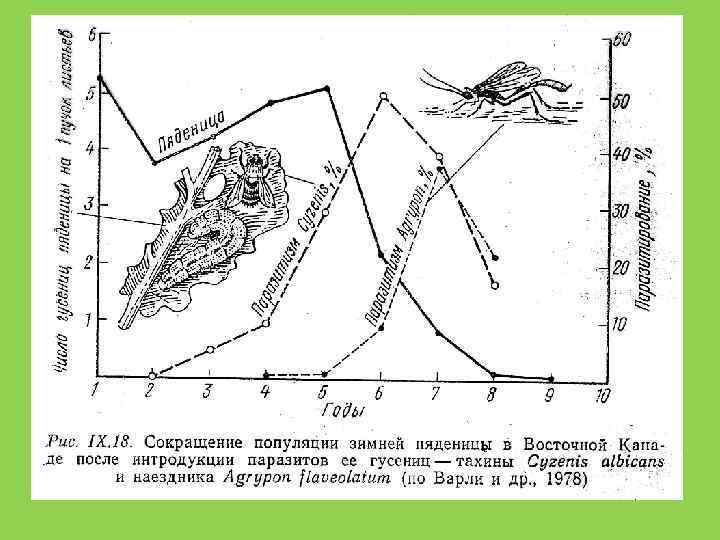
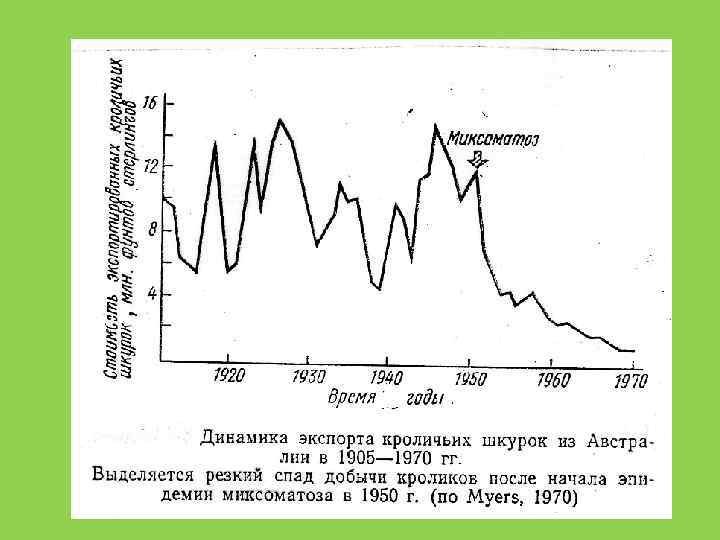

Кактусовая огневка (Cactoblastis cactorum) и опунция http: //en. wikipedia. org/wiki/Cactoblastis_cactorum
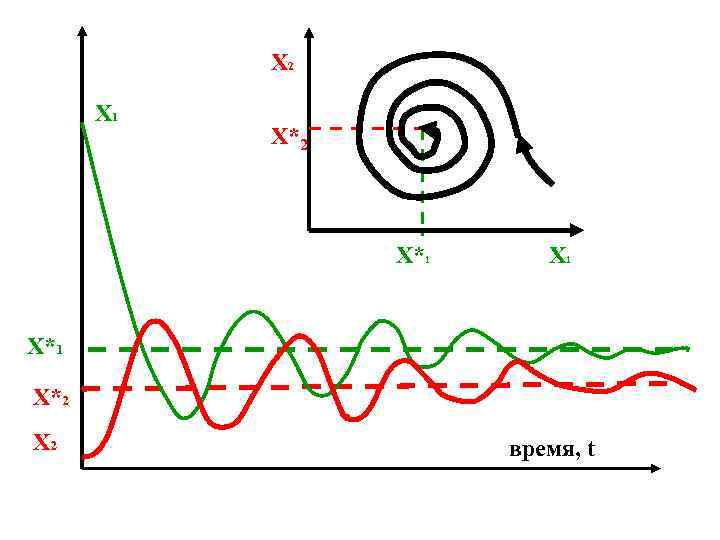
X 2 X 1 X*2 X*1 X 1 X*2 X 2 время, t
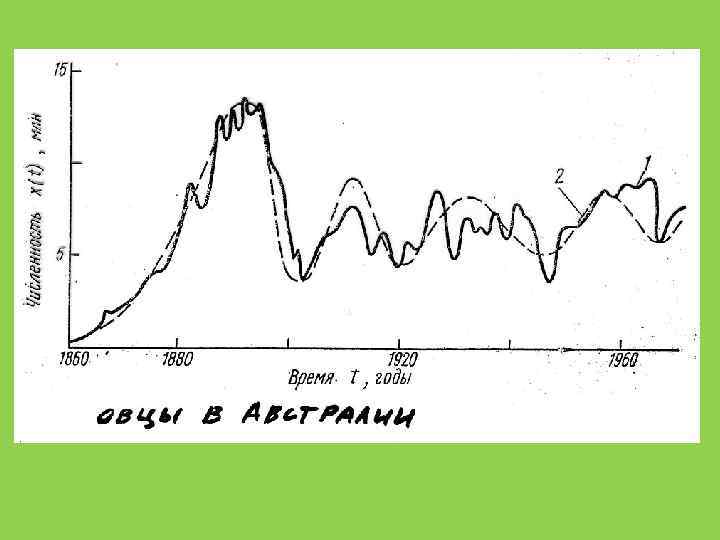
Лекция 7-8 биологи.pptx