Взаимодействие ускоренных ионов с веществом часть 3 3

Взаимодействие ускоренных ионов с веществом (часть 3) 3. 1. Пробеги ионов в веществе. 3. 2. Распределение имплантированных ионов по их пробегам в веществе. 3. 3. Пространственное распределение имплантированной примеси. 3. 4. Пространственное распределение потерь энергии ускоренных ионов в веществе. 1

3. 1. Пробеги ускоренных ионов в веществе ● ● ● Полный (траекторный) пробег R – длина пути, который прошел ион до остановки. Проективный пробег Rp – проекция пути (полного пробега) на нормаль к поверхности мишени. Страгглинг полного пробега либо проективного пробега – среднеквадратичное отклонение полного либо проективного пробега, т. е. дисперсия распределения пробегов. Поперечный пробег – расстояние, на которое сместится ион до своей остановки относительно начального направления своего движения. Векторный пробег – длина вектора, который можно провести от точки начала движения иона в веществе к точке его остановки. 2

3. 1. Пробеги ускоренных ионов в веществе Если - энергия, которую теряет тормозящийся ион на отрезке пути d. R, тогда - расстояние, которое проходит ион, теряя энергию d. E. Следовательно, полный пробег R ускоренного иона в веществе равен: (1) 3

3. 1. Пробеги ускоренных ионов в веществе ● Расчет пробегов с использованием приведенных параметров Расчеты пробегов в приближении Юдина В. В. Выглядят следующим образом: . (2) Для расчета ядерных потерь используем формулу (15) из части 2; для расчета электронных потерь – формулы (16), (17) оттуда же. 4

3. 1. Пробеги ускоренных ионов в веществе ● Расчет пробегов с использованием приведенных параметров (продолжение) Интегрируя (2), получаем: . (3) где arctg подставляется в радианах. Средний полный пробег рассчитывается в соответствии с (12) из части 2: (4) 5

3. 1. Пробеги ускоренных ионов в веществе ● Расчет пробегов с использованием приведенных параметров (продолжение) Проективный пробег связан с полным пробегом следующим образом: (5) где f – корректирующая поправка, обусловленная ядерным торможением: (6) Здесь εn – полная энергия, затраченная ионом на упругие столкновения, которую Юдин В. В. аппроксимирует как: (7) 6

3. 2. Пространственное распределение имплантированных ионов по пробегам Так как: - число соударений, которое испытал ион, - величина потерь энергии в каждом соударении носят случайный характер, то: - траектория каждого иона индивидуальна, - имеется некоторое распределение P ионов по пробегам R. P(R, E 0) – плотность вероятности того, что ион с начальной энергией Е 0 пройдет в веществе путь, равный R. 7

3. 2. Пространственное распределение имплантированных ионов по пробегам Современные методы расчета функции Р для относительно медленных ионов (скорости которых меньше средних скоростей движения электронов в атомах) базируются на модели Линдхарда, Шарффа, Шиотта (ЛШШ), которая была предложена в начале 60 -х годов. 8

3. 2. Пространственное распределение имплантированных ионов по пробегам Основные допущения модели ЛШШ следующие: • вещество, с которым взаимодействует ускоренный ион, является однородным и изотропным, т. е. мишени аморфные; • упругие и неупругие взаимодействия происходят независимо друг от друга; • потери энергии в каждом акте соударения предполагаются много меньшими, чем энергия иона, что позволяет использовать приближение малой передачи энергии и упрощает расчет; • флуктуация потерь энергии иона в упругих соударениях существенно превосходит таковые для неупругих. 9

3. 2. Пространственное распределение имплантированных ионов по пробегам Функция P(E, R) может быть получена из решения кинетического уравнения, которое имеет следующий вид: (8) Здесь dσ(E, T) – сечение упругого взаимодействия ускоренного иона с энергией Е с атомом вещества с передачей энергии Т; Se(E) – электронная тормозная способность вещества; Nяд – ядерная плотность вещества мишени. 10

3. 2. Пространственное распределение имплантированных ионов по пробегам Решение кинетического уравнения (8) представляет собой очень трудную задачу. В принципе, можно получить искомую функцию Р(R, E), если рассчитать такие интегральные характеристики распределения, как его моменты. Для абсолютно точного нахождения функции плотности распределения Р необходимо знать все ее моменты, что в общем случае невозможно. 11

3. 2. Пространственное распределение имплантированных ионов по пробегам Задачу можно облегчить. Для этого разработан следующий подход для решения этого уравнения: - заранее из каких-либо дополнительных соображений предполагают вид функции, аппроксимирующей решение этого уравнения; затем подбирают параметры, чтобы несколько низших моментов, характеризующих аппроксимирующую функцию, совпали с теми же моментами для искомой. 12

3. 2. Пространственное распределение имплантированных ионов по пробегам В теории вероятности моментом распределения порядка n есть величина: (9) а n-м центральным моментом: (10) При этом (11) 13

3. 2. Пространственное распределение имплантированных ионов по пробегам ● Средний полный пробег (математическое ожидание P(R, E): ● Страгглинг полного пробега (дисперсия P(R, E)): 14

3. 2. Пространственное распределение имплантированных ионов по пробегам Свойства функции P(E, R): ● P(E, R) – гладкая, имеющая один максимум, и при R->∞ обращается в нуль; ● соотношение (11) выполняется для ионов с энергиями, превышающими единицы килоэлектронвольт и при углах падения, не очень далеких от нормали; ● P(E, R), как правило, имеет умеренную асимметрию, и во многих случаях эта асимметрия очень мала. 15

3. 2. Пространственное распределение имплантированных ионов по пробегам Одна из наиболее часто используемых аппроксимирующих функций для P(E, R) – гауссово распределение: (12) Здесь - средний полный пробег (математическое ожидание величины полных пробегов); - дисперсия полных пробегов; - среднеквадратичное отклонение или страгглинг полных пробегов). 16

3. 3. Пространственное распределение имплантированной примеси Для построения функции f(E, x) - распределения имплантированной примеси по глубине мишени - необходимо знать два первых момента: - средний проективный пробег , - страгглинг проективного пробега. (13) Здесь D – доза облучения (ион/см 2) – количество ионов, упавших на единицу площади мишени за время облучения. Из (7) видно, что максимум концентрации примеси должен приходиться на глубину, равную величине среднего проективного пробега при данной величине начальной энергии ионов. 17

3. 4. Пространственное распределение потерь энергии ускоренных ионов в веществе Для построения функции пространственного распределения потерь энергии иона важно определить зависимость P(E 0, E, x) – плотность вероятности того, что ион с начальной энергией E 0 имеет энергию Е на глубине х. 18

3. 4. Пространственное распределение потерь энергии ускоренных ионов в веществе Если: - построим функцию P(E 0, E, x); - рассчитаем ядерную Sn и электронную Se тормозные способности, то сможем вычислить на любой заданной глубине мишени х: - линейные потери энергии иона на ядерной торможение (Qn(x)); - линейные потери энергии иона на электронное торможение (Qе(x)), - суммарные линейные потери энергии иона (Q(x)). 19

3. 4. Пространственное распределение потерь энергии ускоренных ионов в веществе Линейные потери энергии иона на глубине х: (14) (15) (16) 20

3. 4. Пространственное распределение потерь энергии ускоренных ионов в веществе Для функции P(E 0, E, x) Маннингом и Мюэллером предложена следующая аппроксимация: (17 ) 21

3. 4. Пространственное распределение потерь энергии ускоренных ионов в веществе Схема расчета линейных потерь энергии ускоренных ионов в веществе 1. Расчет ядерной Sn и электронной Se тормозных способностей. При выборе расчетных моделей принимать во внимание диапазон энергий ионов, а также сорт ионов, для которых предполагается делать расчет. Очень часто при начальных энергиях ионов, соответствующих , для расчета Sn используют потенциалы и сечения Линдхарда (ф-лы (15), (18) из части 2) ; для расчета Se используют модель непрерывного торможения Линдхарда в случае достаточно тяжелых ионов (ф-лы (16)-(18) из части 2), а для легких ионов используют экспериментально полученные сечения электронного торможения. 22

3. 4. Пространственное распределение потерь энергии ускоренных ионов в веществе Схема расчета линейных потерь энергии ускоренных ионов в веществе (продолжение) 2 Расчет проективных пробегов и их страгглингов. 3. Расчет функции P(E 0, E, x) по формуле (17). 4. Расчет линейных потерь энергии по формулам (14)-(16). 23

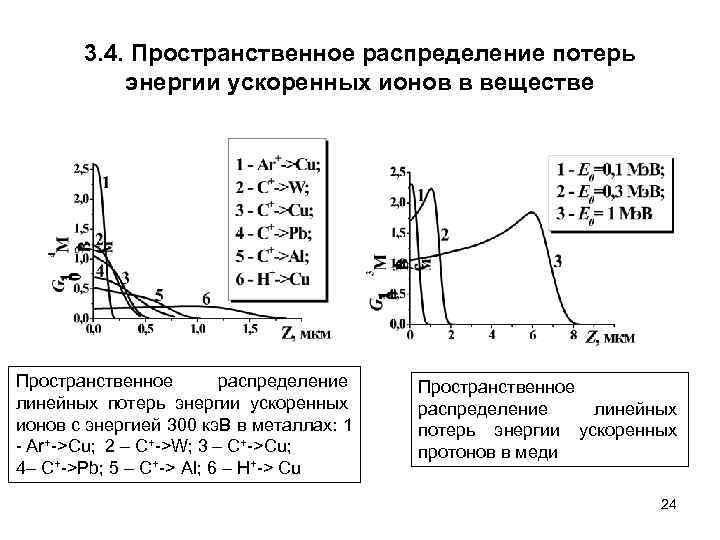3. 4. Пространственное распределение потерь энергии ускоренных ионов в веществе Пространственное распределение линейных потерь энергии ускоренных ионов с энергией 300 кэ. В в металлах: 1 - Ar+->Cu; 2 – C+->W; 3 – C+->Cu; 4– C+->Pb; 5 – C+-> Al; 6 – H+-> Cu Пространственное распределение линейных потерь энергии ускоренных протонов в меди 24

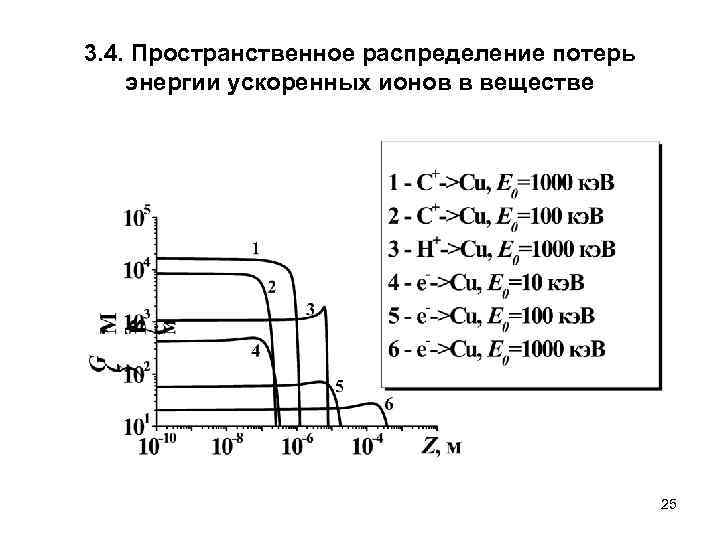3. 4. Пространственное распределение потерь энергии ускоренных ионов в веществе 25