ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ Полное проницание

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ

Полное (проницание) – все образующие одной поверхности пересекаются со второй поверхностью. Линия пересечения распадается на две отдельные кривые Частичное (врезание)– часть образующих одной поверхности пересекается частью образующих другой. Линия пересечения – замкнутая пространственная кривая

Теорема 1 Если две поверхности пересекаются по одной плоской кривой, то существует и другая плоская кривая, по которой они пересекаются

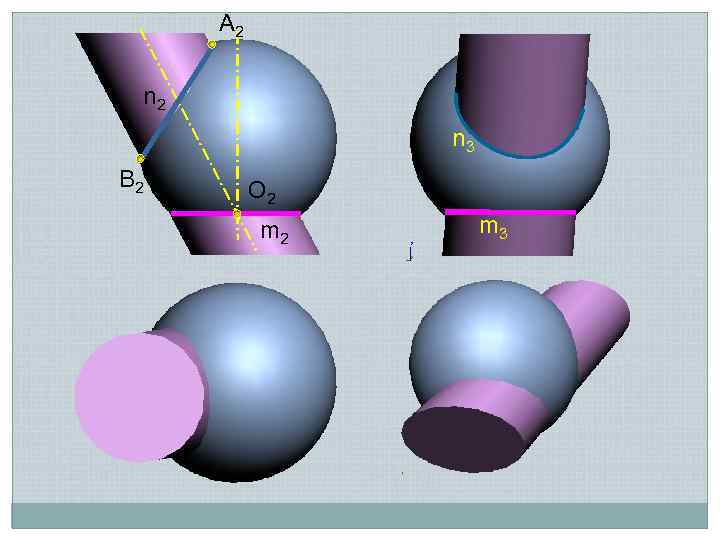A 2 n 3 B 2 O 2 m 3

Одностороннее внутреннее соприкасание – пересекающиеся криволинейные поверхности имеют в одной точке общую плоскость касания Линия пересечения – замкнутая пространственная кривая, пересекающаяся сама с собой в точке касания (точка самопересечения)

Двойное соприкасание – пересекающиеся криволинейные поверхности имеют две общие касательные плоскости В пересечении участвуют все образующие одной поверхности и все образующие второй

Теорема (о двойном касании) Если две поверхности имеют касание в двух точках M и N, то линия перехода распадается на две плоские кривые 2 -го порядка, плоскости которых проходят через отрезок MN, соединяющий точки касания M N

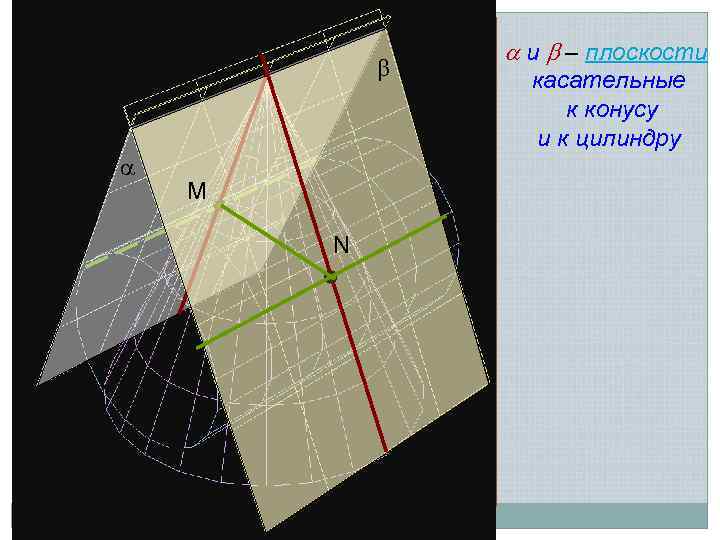M N и – плоскости касательные к конусу и к цилиндру

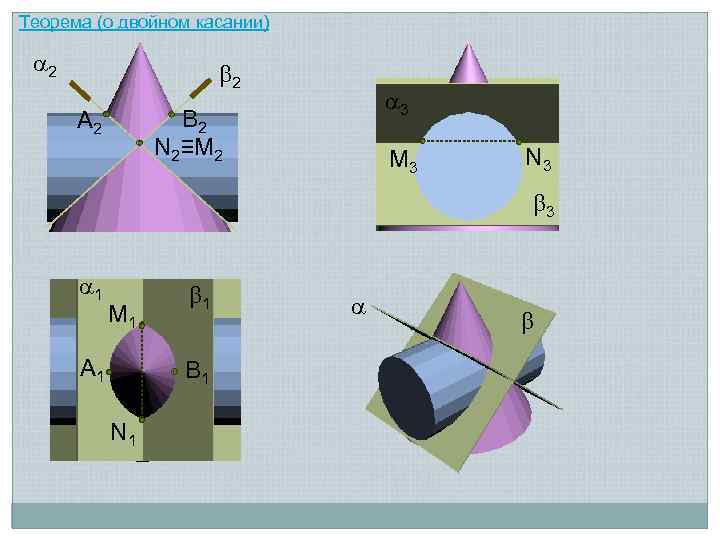Теорема (о двойном касании) 2 2 3 B 2 N 2≡M 2 A 2 M 3 N 3 3 1 M 1 A 1 1 B 1 N 1

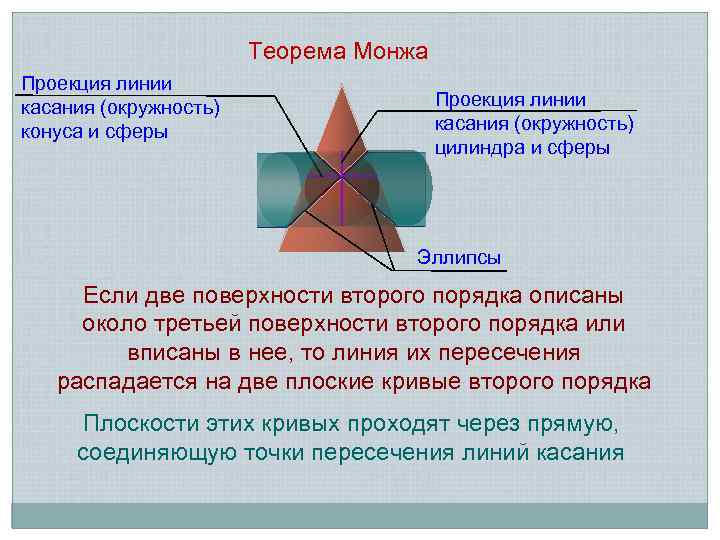Теорема Монжа Проекция линии касания (окружность) конуса и сферы Проекция линии касания (окружность) цилиндра и сферы Эллипсы Если две поверхности второго порядка описаны около третьей поверхности второго порядка или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка Плоскости этих кривых проходят через прямую, соединяющую точки пересечения линий касания