Взаимное пересечение поверхностей геометрических тел Определение линии

Взаимное пересечение поверхностей геометрических тел

Определение линии пересечения двух поверхностей геометрических тел • Способ вспомогательных • СПОСОБ ВСПОМОГАТЕЛЬНЫХ СФЕР параллельных секущих плоскостей. • Их применение основано • Используется тогда, на свойстве соосных когда секущие плоскости поверхностей вращения пересекают поверхности пересекаться по по простым линиям окружностям. (окружностям или • Ось поверхности прямым). вращения • Примеры: пересечение перпендикулярна П 1 сфер и конических или П 2 (окружности поверхностей. проецируются в натуральную величину).

Способ вспомогательных секущих плоскостей. Для построения линии пересечения заданных поверхностей удобно в качестве вспомогательных поверхностей использовать серию горизонтальных плоскостей, перпендикулярных оси конуса, которые пересекают цилиндр и конус по окружностям. На пересечении этих окружностей находят точки искомой линии.

Вспомогательные плоскости выбираются с таким расчетом, чтобы в пересечении их с каждой из данных поверхностей получились простые и удобные для вычерчивания линии, т. е. прямые или окружности.

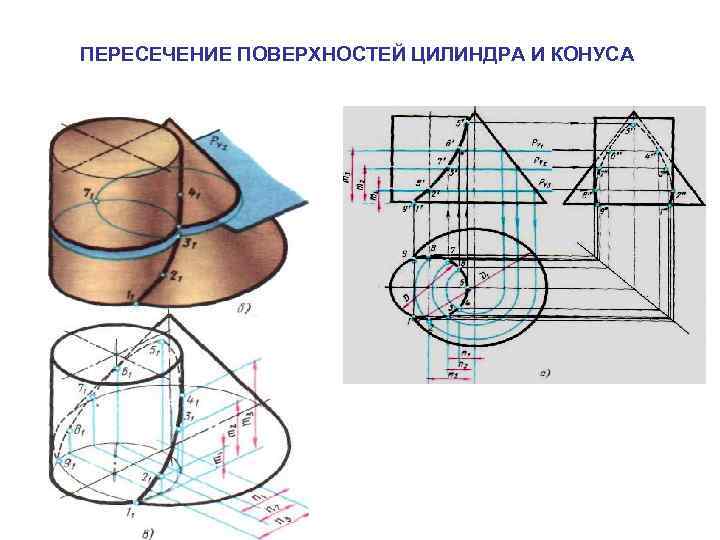ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ЦИЛИНДРА И КОНУСА

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ЦИЛИНДРА И КОНУСА

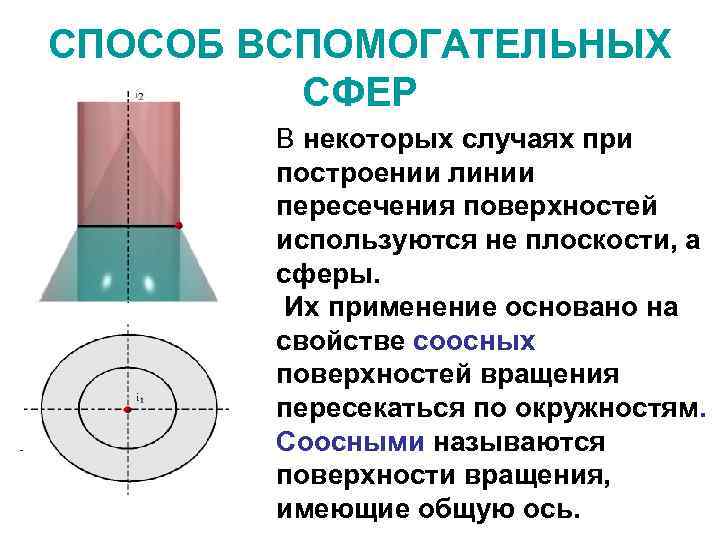СПОСОБ ВСПОМОГАТЕЛЬНЫХ СФЕР В некоторых случаях при построении линии пересечения поверхностей используются не плоскости, а сферы. Их применение основано на свойстве соосных поверхностей вращения пересекаться по окружностям. Соосными называются поверхности вращения, имеющие общую ось.

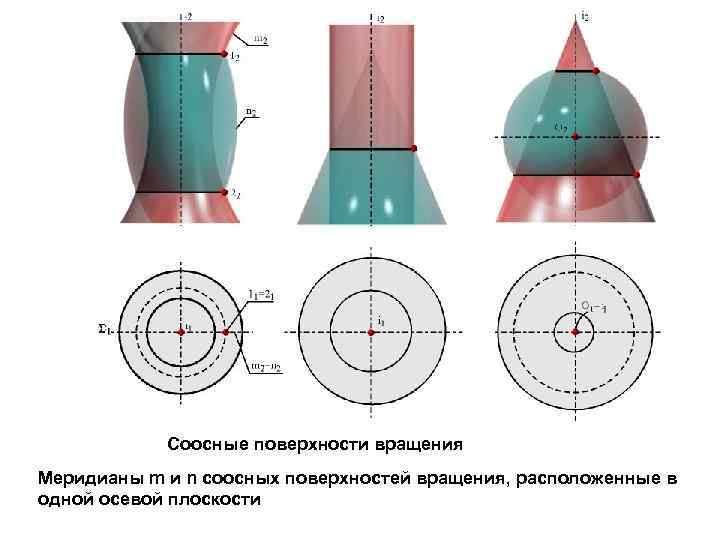Соосные поверхности вращения Меридианы m и n соосных поверхностей вращения, расположенные в одной осевой плоскости

• В отличие от метода вспомогательных секущих плоскостей метод вспомогательных сфер имеет преимущество, так как при построении фронтальной проекции линии пересечения поверхностей не используются две другие проекции.

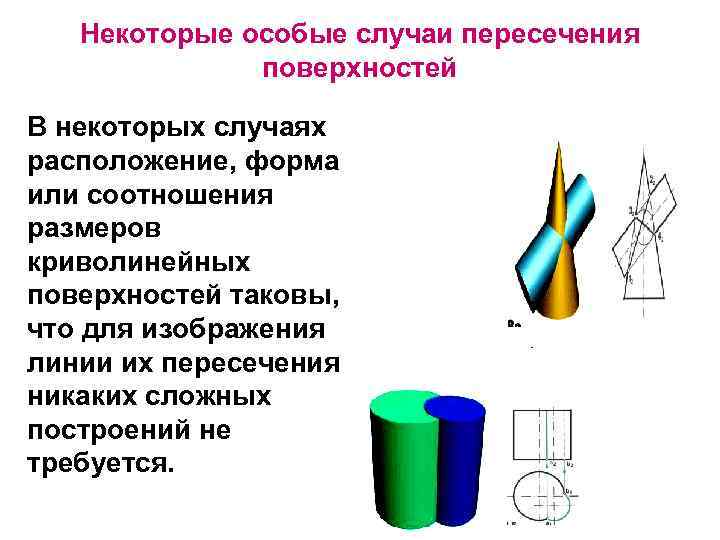Некоторые особые случаи пересечения поверхностей В некоторых случаях расположение, форма или соотношения размеров криволинейных поверхностей таковы, что для изображения линии их пересечения никаких сложных построений не требуется.

Задание по карточке № 3 • Выполнить в трех проекциях чертеж изображенных геометрических тел. Построить линии пересечения (перехода) поверхностей этих тел.

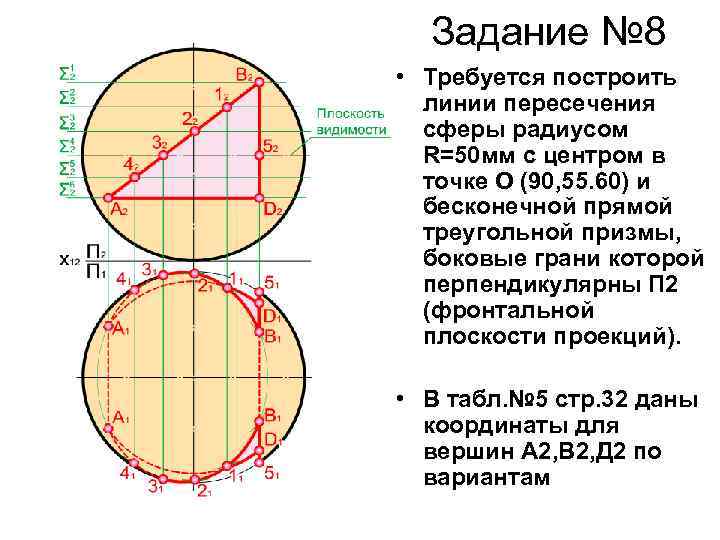Задание № 8 • Требуется построить линии пересечения сферы радиусом R=50 мм с центром в точке О (90, 55. 60) и бесконечной прямой треугольной призмы, боковые грани которой перпендикулярны П 2 (фронтальной плоскости проекций). • В табл. № 5 стр. 32 даны координаты для вершин А 2, В 2, Д 2 по вариантам

Вид спереди

Вид сверху

Вид сверху

«Машиностроительное черчение» под редакцией Г. П. Вяткина. М. , 1977 (стр. 67, рис. 152)

На рисунке показаны характерные точки, в которых на горизонтальной проекции изменяется видимость.

Алгоритм построения точек пересечения поверхностей • 1. - Находят экстремальные (очевидные) точки: самые высокие, самые низкие, которые принадлежат линии пересечения и проходят через оси вращения; • 2. – Вводим секущие плоскости и их обозначаем; • 3. – Строим линии пересечения (параллель R) и (параллель радиуса r); • 4. - Определяем точки пересечения этих линий (R, r); • 5. - Вводим промежуточные точки 1, 2, 3, 4, и т. д. , которые строят применяя алгоритм; • 6. – Определяем видимость на П 1, П 2 поверхностей.

Конец лекции