Взаимно перпендикулярные прямые и плоскости Признаки перпендикулярности 1

Взаимно перпендикулярные прямые и плоскости Признаки перпендикулярности 1. 2. 3. 4. Две прямые перпендикулярны, если угол между ними равен 90° Прямая перпендикулярна плоскости если она перпендикулярна двум пересекающимся прямым, принадлежащим плоскости Прямая, перпендикулярная плоскости, перпендикулярна любой прямой, принадлежащей плоскости Если плоскость проходит через перпендикуляр к другой плоскости, то она перпендикулярна этой плоскости

Проекции прямого угла Теорема № 1 Если одна сторона прямого угла параллельна плоскости проекций, а вторая является прямой общего положения, то прямой угол проецируется на эту плоскость проекций без искажения, т. е. в прямой угол

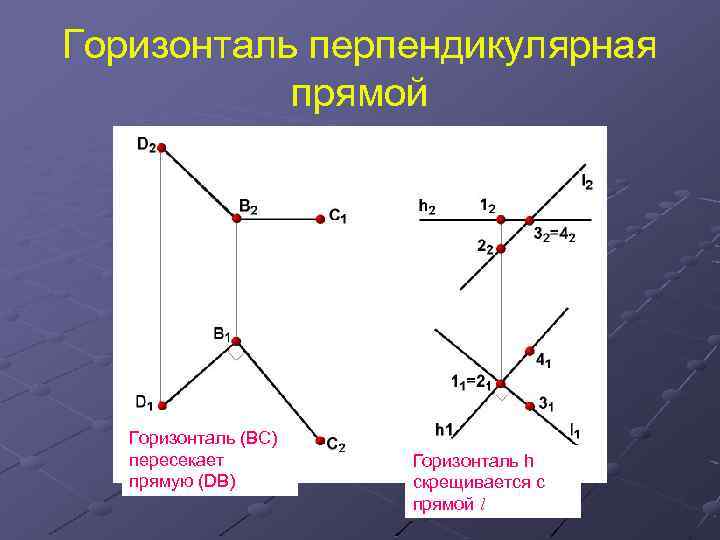Горизонталь перпендикулярная прямой Горизонталь (ВС) пересекает прямую (DB) Горизонталь h скрещивается с прямой l

Фронталь перпендикулярная прямой Фронталь (ВС) пересекает прямую (DB) Фронталь f скрещивается с прямой l

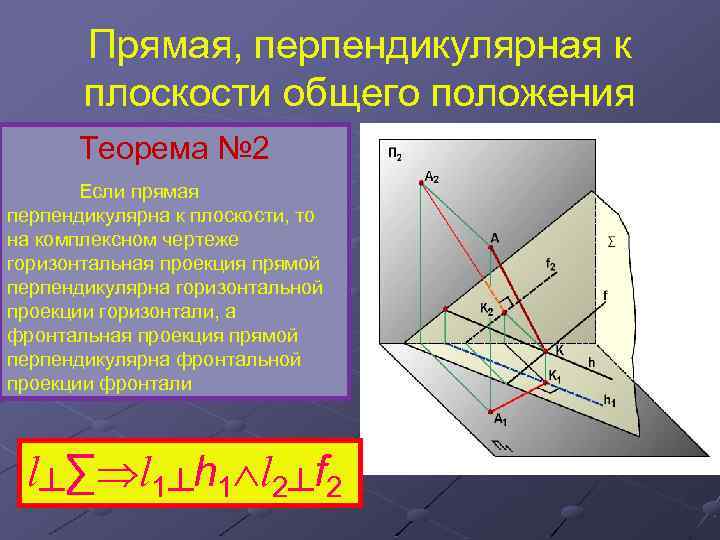Прямая, перпендикулярная к плоскости общего положения Теорема № 2 Если прямая перпендикулярна к плоскости, то на комплексном чертеже горизонтальная проекция прямой перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали l┴∑ l 1┴h 1 l 2┴f 2

Основные задачи Задача № 1 Опустить перпендикуляр из т. А на плоскость общего положения A 2 h 2 m 2 l┴∑ l 1┴h 1 l 2┴f 2 n 2 m 1 n 1 h 1 A 1

Основные задачи Задача № 1 Опустить перпендикуляр из т. А на плоскость общего положения f 2 A 2 h 2 m 2 l┴∑ l 1┴h 1 l 2┴f 2 n 2 f 1 m 1 n 1 h 1 A 1

Основные задачи Задача № 1 Опустить перпендикуляр из т. А на плоскость общего положения l 2 f 2 A 2 h 2 m 2 l┴∑ l 1┴h 1 l 2┴f 2 n 2 f 1 l 1 m 1 n 1 h 1 A 1

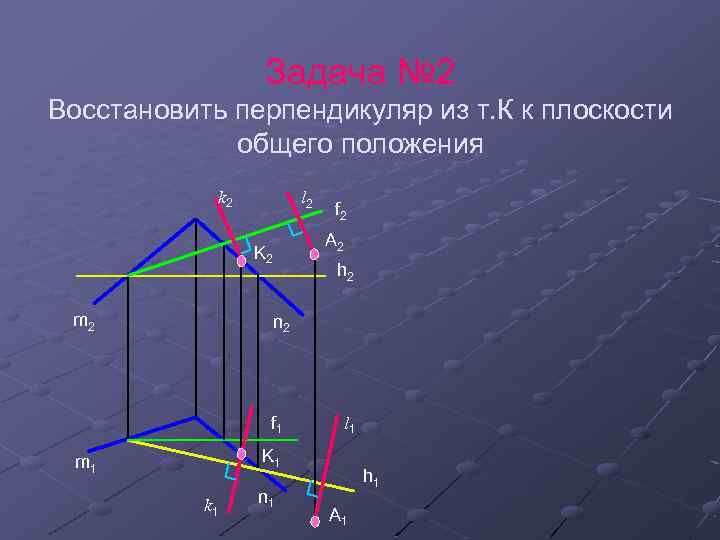Задача № 2 Восстановить перпендикуляр из т. К к плоскости общего положения k 2 l 2 A 2 K 2 m 2 f 2 h 2 n 2 f 1 l 1 K 1 m 1 k 1 n 1 h 1 A 1

Задача № 3 Через т. А провести плоскость ∑, перпендикулярную прямой общего положения l 2 A 2 f 2 h 2 l┴∑ l 1┴h 1 l 2┴f 2 f 1 A 1 l 1 h 1

Задача № 3 а Через т. А провести плоскость ∑, перпендикулярную горизонтали ∑ 2=П 2 A 2 h 2 ∑ 1 h 1 A 1

Задача № 3 б Через т. А провести плоскость ∑, перпендикулярную фронтали ∑ 2 f 2 A 2 ∑ 1=П 1 f 1 A 1

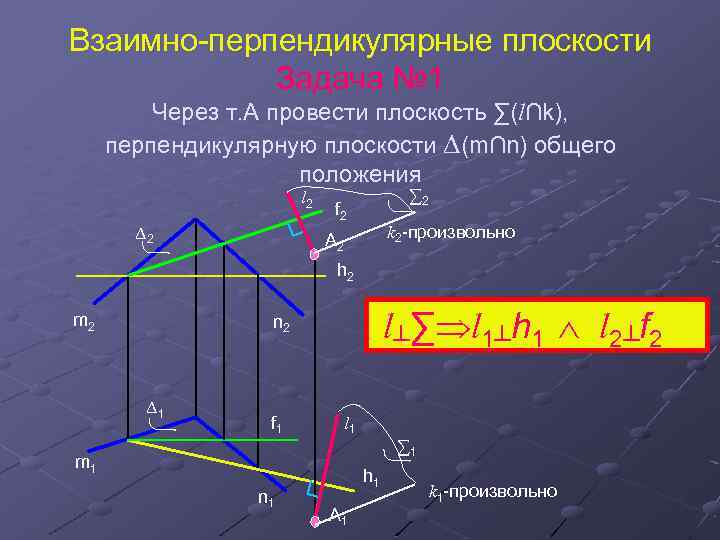Взаимно-перпендикулярные плоскости Задача № 1 Через т. А провести плоскость ∑(l∩k), перпендикулярную плоскости ∆(m∩n) общего положения l 2 ∆2 ∑ 2 f 2 k 2 -произвольно A 2 h 2 m 2 l┴∑ l 1┴h 1 l 2┴f 2 n 2 ∆1 f 1 l 1 ∑ 1 m 1 n 1 h 1 A 1 k 1 -произвольно

Взаимно-перпендикулярные плоскости Задача № 2 Через т. А провести плоскость ∑(h∩f), перпендикулярную плоскости ∆(m∩n) общего положения ∆2 f 2 A 2 m 2 ∑ 2 h 2 n┴∑ n 1┴h 1 n 2┴f 2 n 2 ∆1 h 1 m 1 A 1 n 1 ∑ 1 f 1

Плоскость, перпендикулярная одновременно двум плоскостям Плоскость, перпендикулярная линии пересечения двух плоскостей Плоскость, образованная перпендикулярами, проведенными из одной точки к каждой из заданных плоскостей

Взаимно-перпендикулярные прямые общего положения Основные положения 1. Прямая, перпендикулярная плоскости, перпендикулярна любой прямой, принадлежащей плоскости 2. Если две прямые взаимно-перпендикулярны, то через каждую из них можно провести плоскость, перпендикулярную к другой прямой Таким образом построение сводится к построению плоскости, перпендикулярной к заданной прямой общего положения

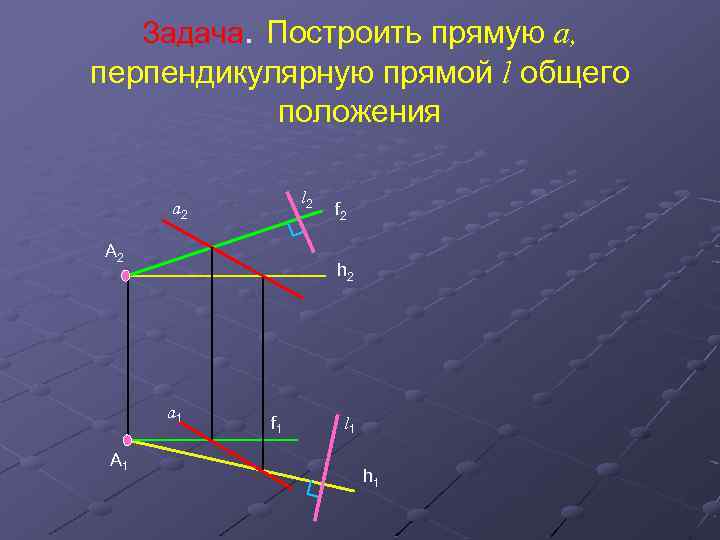Задача. Построить прямую a, перпендикулярную прямой l общего положения l 2 а 2 A 2 h 2 а 1 A 1 f 2 f 1 l 1 h 1

Комплексные задачи в которых на искомый элемент наложены два и более условий Последовательность решения: 1. Проводится анализ • Что ищем? • Каким геометрическим множествам принадлежит искомый элемент 2. Проводится исследование – существует ли решение и сколько решений может иметь задача 3. Составляется алгоритм решения задачи – записывается последовательность построений для определения искомого элемента